基于ICS-LSSVM的电动汽车锂电池SOC预测
2023-01-15王骏骏
王骏骏
(国网十堰供电公司,湖北 十堰 442099)
随着国家“双碳”目标的提出,无污染、零排放的电动汽车成为未来汽车的发展方向[1-2]。作为电动汽车的动力来源,动力电池是保障电动汽车安全行驶的重要基础。锂电池具有能量密度高、自放电率低、使用寿命长等多种优点,目前已成为电动汽车动力电池的主流电源[3]。为了防止动力电池出现过充、过放等损伤电池寿命的现象,有必要对锂电池的荷电状态(state of charge, SOC)预测进行研究。
目前,国内外专家学者已在锂电池SOC预测方面进行了大量研究。文献[4]将人工蜂群(artificial bee colony,ABC)算法和随机森林(random forest,RF)算法相结合,得到ABC-RF优化算法,采用ABC-RF算法对扩展卡尔曼滤波(extended kalman filter,EKF)进行优化,建立了基于ABC-RFEKF的锂电池SOC估算模型,取得了较高的SOC估算精度。文献[5]为了解决反向传播(back propagation,BP)神经网络容易陷入局部最优的问题,采用自适应变异粒子群算法(adaptive mutation particle swarm optimization,AMPSO)对BP神经网络进行优化,建立了基于AMPSO-BP神经网络的锂电池SOC预测模型。文献[6]提出一种基于改进蚁群算法优化粒子滤波的锂电池SOC预测方法,解决了传统粒子滤波法预测SOC时带来的粒子贫化问题,提高了锂电池SOC估算精度。文献[7]为了提高锂电池SOC预测精度,以温度、电流和电压为输入量,以锂电池SOC为输出量,建立了基于高斯过程回归的锂电池SOC预测模型。上述文献虽然都能对锂电池SOC进行预测,但预测精度有待进一步提高。
针对现有锂电池SOC预测研究中存在的不足,本文对传统布谷鸟搜索(cuckoo search,CS)算法进行改进,采用改进布谷鸟算法(improved cuckoo search,ICS)对最小二乘支持向量机(least squares support vector machine,LSSVM)的惩罚参数和核函数宽度进行优化,建立基于ICS-LSSVM的电动汽车锂电池SOC预测模型,并用锂电池充放电试验数据对模型的正确性和实用性进行验证。
1 布谷鸟搜索算法及其改进
1.1 布谷鸟搜索算法
布谷鸟搜索算法CS是由数学家YANG和DEB于2009年提出的一种新型智能算法,CS算法遵循布谷鸟借窝产卵繁殖和Lévy飞行2大原理[8]。相比于其他优化算法,CS算法所需参数少,全局搜索能力强,目前被广泛应用于交通、通信、电力等各个领域。
CS算法满足3个理想化的假设:①每只布谷鸟只产1个卵,并随机选择任何1个宿主鸟窝进行孵化;②布谷鸟搜索过程满足精英保留机制;③鸟窝数目固定,布谷鸟的卵被宿主鸟发现的概率为pa∈[0,1],一旦被宿主鸟发现,该鸟窝会被抛弃,布谷鸟需要重新寻找新的鸟窝。
CS算法优化原理如下。
对于d维优化问题,令布谷鸟种群X为
X={x1,x2,x3,…,xd}
(1)
利用莱维飞行对鸟窝位置进行更新。
(2)
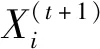
L(λ)~u=t-λ,1<λ≤3
(3)
可以得到:
(4)
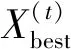
(5)
式中:Γ为Gamma函数,其概率分布的方差与均值均为无界。
1.2 布谷鸟算法改进
在标准布谷鸟算法中,布谷鸟的卵被发现的概率pa和步长控制量α在寻优迭代过程中始终为固定值,在算法迭代初期全局搜索能力不够,到了后期会影响算法的局部寻优能力。为了增强算法在迭代初期的全局搜索性能和保证算法后期的迭代寻优能力,本文将CS算法中布谷鸟的卵被发现的概率pa和步长控制量α进行动态设置,使pa和α的值随着迭代次数变化而动态变化,得到改进布谷鸟算法。
(6)
(7)
式中:pa,max和pa,min分别为布谷鸟的卵被发现概率pa的最大值和最小值;αmax和αmin分别为步长控制量α的最大值和最小值。
研究表明,ICS算法能够提高迭代前期的全局搜索性能和增强迭代后期的局部寻优能力,在算法迭代初期能够增强算法的全局搜索性能,增加适应度值较好解的多样性;到迭代后期,随迭代次数增加,算法局部寻优能力逐渐增强,快速找到全局最优解,避免无效迭代,加快算法收敛。
2 最小二乘支持向量机
最小二乘支持向量机LSSVM是Suykens基于支持向量机(support vector machine,SVM)提出的改进机器学习算法,LSSVM满足结构风险最小化原则,在进行分类和回归时同样需要核函数。LSSVM和SVM的区别在于约束条件和优化指标,等式约束和平方项优化指标使LSSVM计算过程更简便,目前在解决分类、回归问题方面得到广泛应用[8]。
LSSVM进行回归分析的原理可参考文献[9]。多项式核函数、双曲正切核函数和高斯径向基核函数是LSSVM的常用核函数,为了使LSSVM具有更好的拟合能力,本文采用高斯径向基核函数,其表达式为
(8)
式中:σ为核函数宽度。
研究表明,惩罚参数C与核函数宽度σ是2个非常重要的参数,能够直接影响LSSVM的拟合效果[10],为了提高锂电池SOC的预测精度,应采用优化算法对C和σ进行寻优。
3 锂电池SOC预测模型
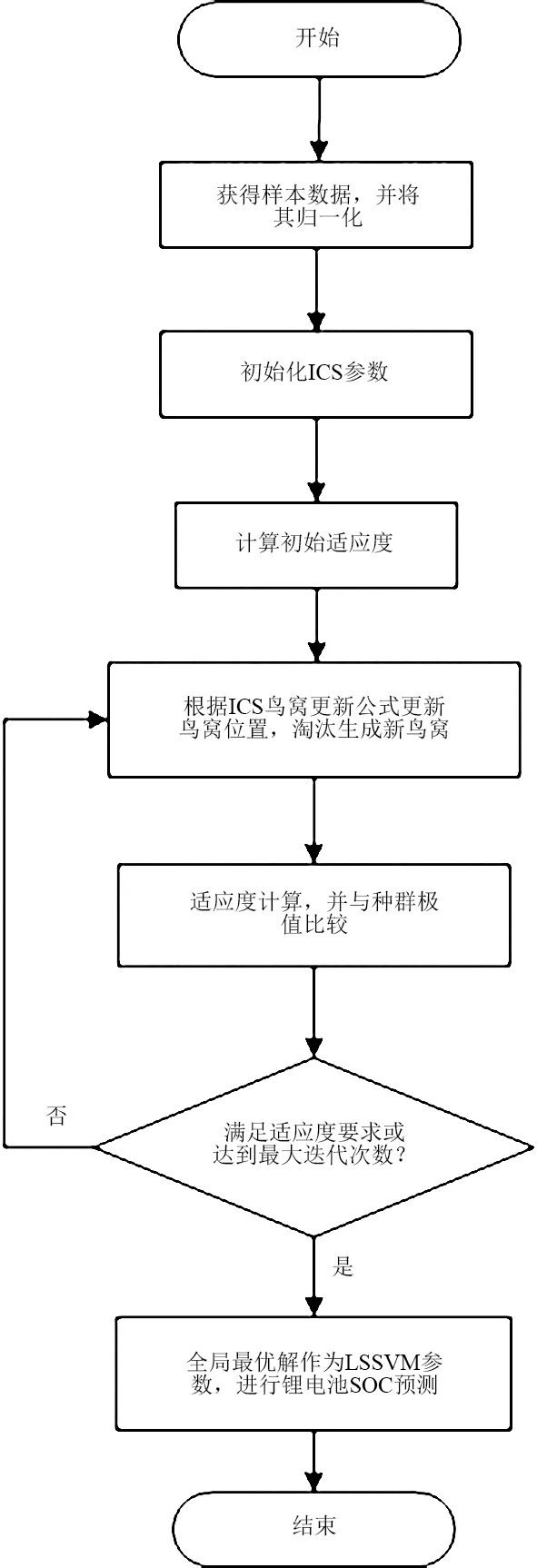
锂电池SOC主要受温度、电压和电流等因素的影响,为了研究锂电池SOC与各影响因素之间的关系,采用LSSVM对锂电池SOC进行回归分析,利用改进布谷鸟算法对LSSVM的C和σ进行寻优,建立基于ICS-LSSVM的电动汽车锂电池SOC预测模型,建模流程如图1所示,建模步骤如下。
a.获得样本数据,并归一化为
(9)
式中:x′i为归一化后的数据;xi为原始值;xmax和xmin分别为xi的最大值和最小值。
b.对ICS的相关参数进行初始化设置,设置鸟窝数量n=100,最大迭代次数Tmax=200,布谷鸟的卵被发现概率的最大值pa,max=1、最小值pa,min=0.005,步长控制量的最大值αmax=0.5、最小值αmin=0.01。
c.初始化LSSVM参数,设置惩罚参数C初始值为100、核函数宽度σ初始值为0.1,搜索范围分别为[0,100]和[0,1]。
d.在C和σ的搜索范围内,利用ICS算法展开搜索,然后把初始解代入LSSVM预测模型中,计算初始适应度值。本文以训练数据的均方根误差为适应度值,均方根误差为
(10)
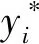
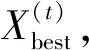
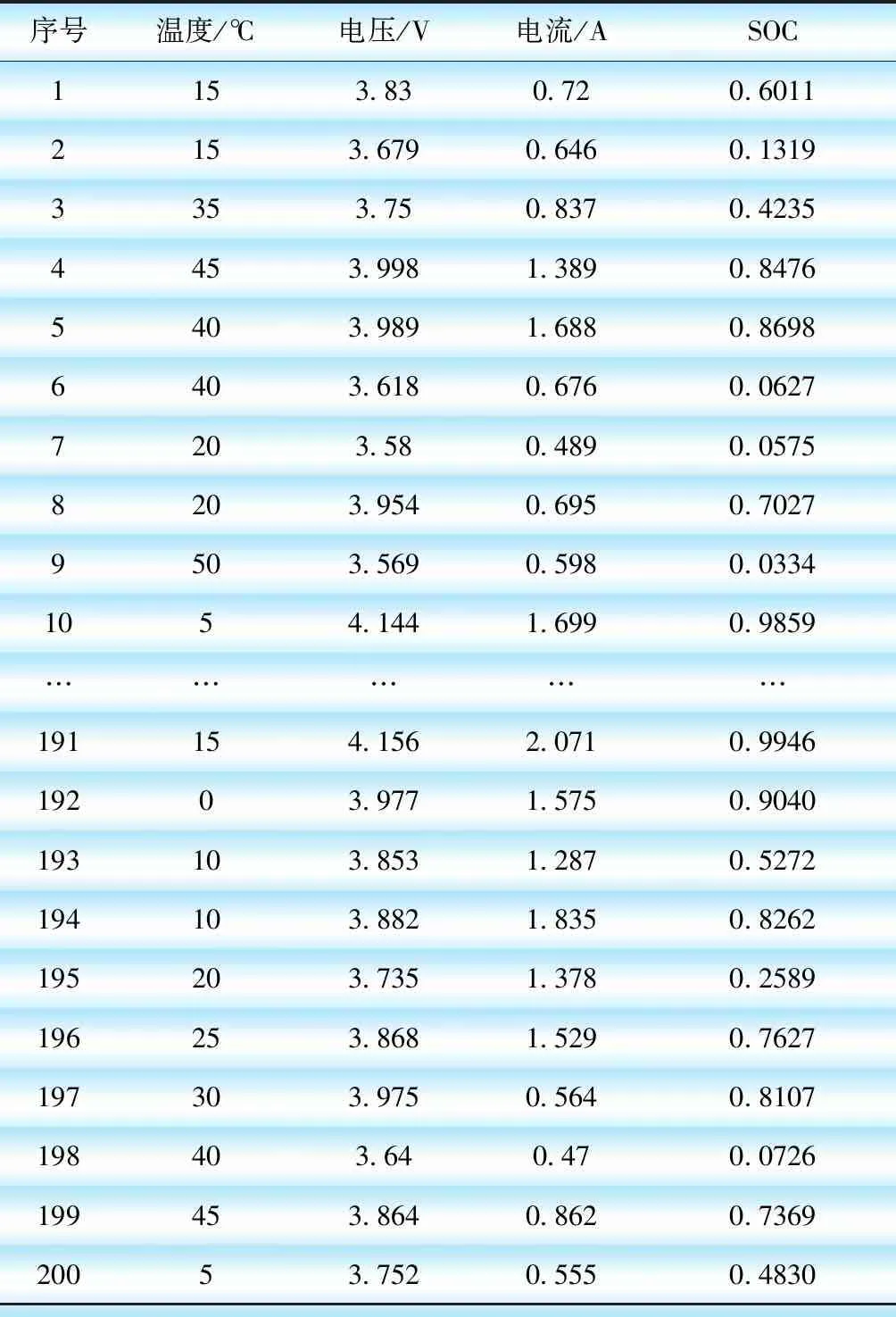
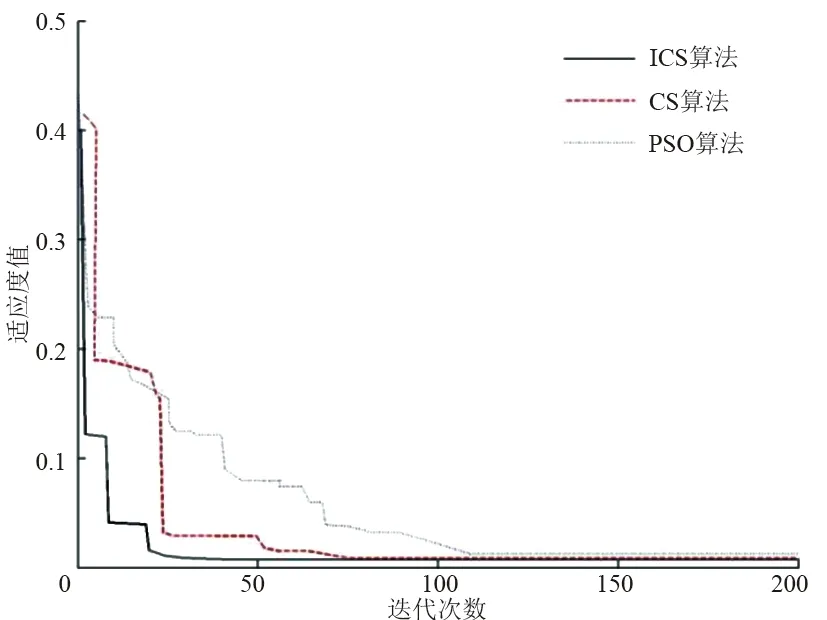
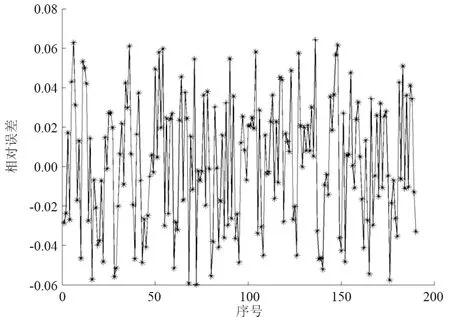
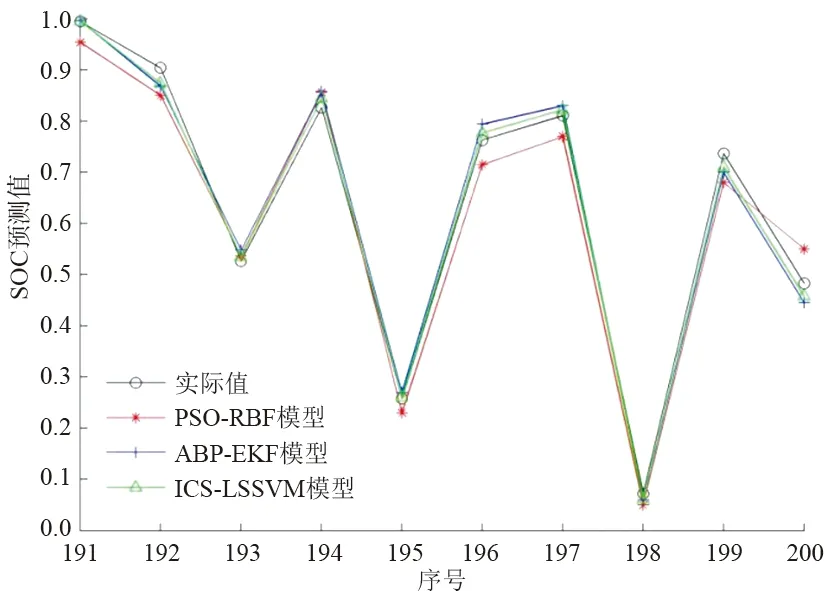
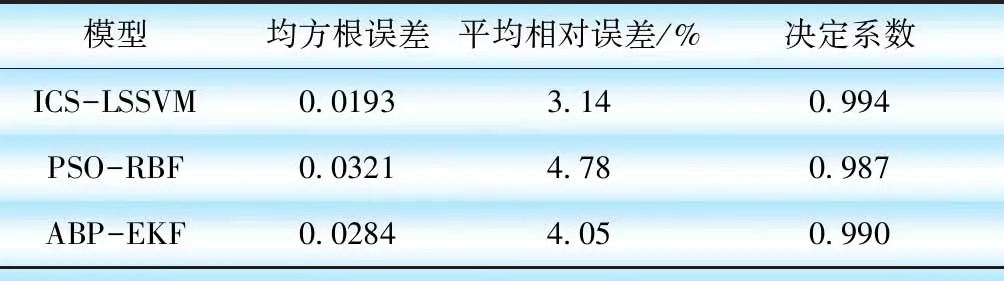
f.随机生成1个概率r,将r值与被发现概率pa进行比较,如果r>pa,则随机淘汰并生成1组新鸟窝位置;如果r h.将步骤g中的C和σ赋给LSSVM模型,即可对测试集样本进行预测。 图1 模型流程 通过电动汽车锂电池(磷酸铁锂)充放电试验获得200组样本数据,单体锂电池额定容量为1.75 Ah、额定电压为4.2 V,部分数据如表1所示。根据建模需要,将200组样本数据分为训练集和测试集,训练集为前190组数据,测试集为后10组数据。 表1 部分样本数据 在MATLAB中进行仿真分析,以温度、电压和电流为输入量,SOC为输出量,建立基于ICS-LSSVM的锂电池SOC预测模型,采用训练集数据进行训练,利用ICS算法对LSSVM的惩罚参数C和核函数宽度σ进行寻优。为了对比分析,采用CS算法和PSO算法分别对C和σ进行寻优,3种优化算法的迭代曲线如图2所示。由图2可知,在达到目标精度时,ICS算法所需迭代次数更少,能够有效减少迭代次数,加快算法收敛。 图2 3种优化算法的迭代曲线 图3给出了基于ICS-LSSVM锂电池SOC预测模型的训练误差。由图3可知,训练集数据的误差为[-0.060,0.0642],且大部分训练误差在±5%以内,模型训练效果较好。 图3 训练集误差 图4 3种模型锂电池SOC预测值 ICS算法获得的最优解C=32.56和σ=1.76,将最优解赋给LSSVM,利用训练好的ICS-LSSVM模型对测试集中10组样本数据进行预测。为了对比分析,分别采用文献[11]和文献[12]中的锂电池SOC预测方法建立PSO-RBF模型和ABP-EKF模型,3种模型锂电池SOC预测值如图4所示。由图4可知,ICS-LSSVM模型的SOC预测值比PSO-RBF模型和ABP-EKF模型更接近锂电池SOC的实际值。 为了进一步对比3种锂电池SOC预测模型的预测效果,采用均方根误差、平均相对误差和决定系数等3种误差评价方法对各模型的预测效果进行综合评价。均方根误差、平均相对误差和决定系数分别为 (11) (12) (13) 采用误差评价指标对ICS-LSSVM模型、PSO-RBF模型和ABP-EKF模型的预测误差进行计算,结算如表2所示。由表2可知,ICS-LSSVM模型的均方根误差、平均相对误差和决定系数分别为0.0193、3.14%和0.994,均方根误差和平均相对误差均小于PSO-RBF模型和ABP-EKF模型,ICS-LSSVM模型对锂电池SOC的预测精度较高。其决定系数大于PSO-RBF模型和ABP-EKF模型,表明ICS-LSSVM模型对样本数据的拟合效果更好。综上所述,本文提出的基于ICS-LSSVM的电动汽车锂电池SOC预测模型能够显著提高锂电池SOC的预测精度。 表2 3种模型的误差指标 a.对CS算法中布谷鸟的卵被发现的概率和步长控制量进行动态设置,以增强算法在迭代初期的全局搜索性能和迭代后期的迭代寻优能力,得到ICS算法。仿真分析表明,ICS算法能够有效减少迭代次数,加快算法收敛。 b.采用ICS算法对LSSVM的惩罚参数和核函数宽度进行优化,建立基于ICS-LSSVM的电动汽车锂电池SOC预测模型,采用磷酸铁锂电池充放电数据进行仿真分析,并与其他模型对比。结果表明,基于ICS-LSSVM的电动汽车锂电池SOC预测模型能够显著提高锂电池SOC的预测精度,验证了模型的正确性和实用性。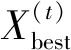
4 仿真分析
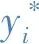
5 结论
