基于组合赋权的水资源承载力综合评价模型构建及应用

金永民

(辽宁省河库管理服务中心(辽宁省水文局)，辽宁 沈阳 110003)

研究水资源的承载力可为水资源的可持续发展提供重要信息[1]。水资源承载力研究有利于明确水资源对社会经济的支撑能力，加深对水资源价值的了解，从而能够建立正确的水资源开发利用观念；同时，水资源承载力的研究可以为城市的经济发展决策以及水资源方面的规划提供依据和支撑[2]。水资源承载力评价指标体系的建立和评价模型的选取是水资源承载力研究中的关键问题，构建科学的水资源承载力评价指标体系，建立水资源承载力综合评价模型，对于区域水资源开发利用和社会经济的可持续发展具有重要的现实指导意义，同时为城市的经济发展决策以及水资源规划提供依据[3]。亟需针对水资源承载力建立科学合理的评价体系，对影响水资源承载力的主要因素进行系统分析，探索适用性较好的评价方法，为此本文分别从水资源、社会经济、生态环境、水管理四个层次选取21个指标构建水资源承载力综合评价指标体系，并采用基于组合赋权的灰色关联度模型建立评价模型，以阜新市为实例，对其区域水资源承载进行综合评价。

1 评价指标体系构建

1.1 评价指标选取

以代表性、可度量性、层次性、动态性和全面性为原则，分别从水资源、社会经济、生态环境、水管理等层面，构建水资源承载力综合评价指标体，具体指标见表1。

表1 水资源承载力综合评价指标体系

1.2 评价等级划分

依据《地表水环境质量标准》(GB 3838—2002)、《地下水环境质量标准》(GB/T 14848—93)、辽宁省地方标准《行业用水定额》(DB21/T 1237—2015)等，参考水资源承载力评价的相关科研成果和文献以及研究区域水资源特点，对评价指标的等级进行划分，见表2。

表2 水资源承载能力综合评价等级划分

2 基于组合赋权的灰色关联度评价模型

采用熵权修正AHP法建立组合赋权模型并与灰色关联度评价模型融合，建立基于组合赋权的灰色关联度评价模型，模型首先需对数据进行标准化处理，其次求出组合权重，同时建立关联系数矩阵，最后确定综合评价矩阵。基于熵权修正AHP法组合赋权的关联度评价流程见图1。

图1 基于熵权修正AHP法组合赋权的关联度评价流程

2.1 建立标准化矩阵

根据指标规范化处理方法，将收集的原始数据转化成标准化矩阵。由于指标体系中各评价指标的数量级、单位量纲均不同，直接进行评价会对结果的准确性产生影响，因此应对各指标先进行标准化处理，建立标准化矩阵。

a.成本指标。这类指标是取值越小越优的指标，采用式(1)的方法处理。

(1)

式中：xi为指标实际值；maxxi为指标最大值；minxi为指标最小值；yi为指标标准化值。

b.效益指标。这类指标是取值越大越优的指标，采用式(2)的方法处理。

(2)

标准化后的数据形成如下：

(3)

2.2 确定参考序列

水资源承载力评价中，选取指标等级标准yik(k=1,2,…,K-1,K)为参考序列。由于水资源承载力指标的等级标准不是一个固定值，而是区间矩阵，在指标标准值转化时应按照式(4)进行转化得到标准值矩阵Sik:

(4)

式中:Sik为指标i等级k的指标等级标准值；Si1为等级Ⅰ对应的标准值；SiK为等级Ⅴ对应的标准值。

为消除物理量纲的影响，应对参考序列进行规范化处理，转换为[0,1]之间的数值。采用式(5)进行参考数列的归一化处理：

(5)

式中:S′ik为归一化的Sik。

2.3 基于熵权修正AHP法的组合赋权

利用层次分析法确定不同准则层每个评价指标的重要性排序，然后根据熵权法确定的权重值计算相邻指标的重要性程度，依次求得每个指标的权重和准则层权重进而确定组合权重，这种组合形式兼顾了主观权重和客观权重的优点。具体步骤如下：

a.确定评价指标的重要性排序。运用AHP法将每个准则层(i=1,2,…,m)的评价指标j=1,2,…,n按重要性从大到小的顺序进行排序。

b.确定相邻指标的重要性之比。根据熵权法计算的评价指标权重，计算第j个属性的权重ej和相邻指标xk-1与xk重要性程度之比rk，见式(6)：

(6)

c.确定指标权重。根据相邻指标的重要性之比rj和式(7)、式(8)，对每个准则层自下而上计算评价指标的修正权重vm，以及第m,m-1,…,3,2个指标权重，同理可得准则层修正权重vi：

(7)

vj-1=rjvj(j=m,m-1,…,3,2)

(8)

确定组合权重。根据确定准则层修正权重vi和评价指标修正权重vm，从而得到相对于目标层的组合权重wj：

wj=vivm

(9)

2.4 计算综合关联度

目前，判断因素序列间灰关联程度的指标主要有邓氏关联度、绝对关联度、T型关联度、斜率关联度等。本文采用应用较为广泛的邓氏关联度，计算关联系数的公式见式(10)：

(10)

根据式(10)，关联系数计算结果的准确性与分辨系数ρ有很大关系，为保证结果的合理性，一般选取ρ=0.5进行计算。根据组合赋权确定的指标权重，采用加权算术平均公式计算关联程度γ：

(11)

式中：wi为各指标权重。

2.5 得到评价结果

根据计算的综合关联度和评价标准，确定水资源承载力综合评价的等级。

3 实例应用

3.1 区域概况

本文选择辽宁省阜新市进行水资源承载力综合评价。阜新市位于辽宁省西部，全市总面积19736km2，是辽宁省14个省辖市中面积最大的城市。受季风气候和地理位置影响，降水量在年内分配极不均匀。冬季主要受西伯利亚冷高压控制，降雪很少，气候寒冷；春季受东南季风影响，雨季较晚，一般要6月开始有大量降雨，7—8月雨量最为充沛，5—8月的雨量几乎占据了全年总降水量的80%。根据第三次水资源评价结果，阜新市水资源总量149157万m3，其中地表水资源量147086万m3，地下水资源量71329万m3，地表水和地下水资源不重复量为2071万m3。

3.2 指标值的确定

2021年为评价年，采用的数据主要来源于《2020年阜新市水资源公报》《2021年阜新市统计年鉴》《阜新市水资源》以及阜新市第三次水资源评价的部分数据。

3.3 评价指标及等级标准化

在指标值确定的基础上，采用标准化处理方法对其评价指标及其对应的等级进行标准化处理，处理结果见表3。

表3 阜新市水资源承载力综合评价指标及等级标准化

3.4 主观权重赋值

针对水资源承载力评价指标体系，邀请10位专家对各层指标的重要性进行打分，根据指标的相对重要程度，采用Saaty九度法[4]构建判断矩阵，一级指标的判断矩阵见表4，各准则层二级指标判断矩阵见表5～表8。利用MATLAB程序求出各个判断矩阵最大特征值以及对应的特征向量，对其进行一致性检验，在对特征向量归一化处理后，确定每个评价指标的主观权重及重要度排序，见表9。

表4 A-B判断矩阵

表5 B1-C判断矩阵

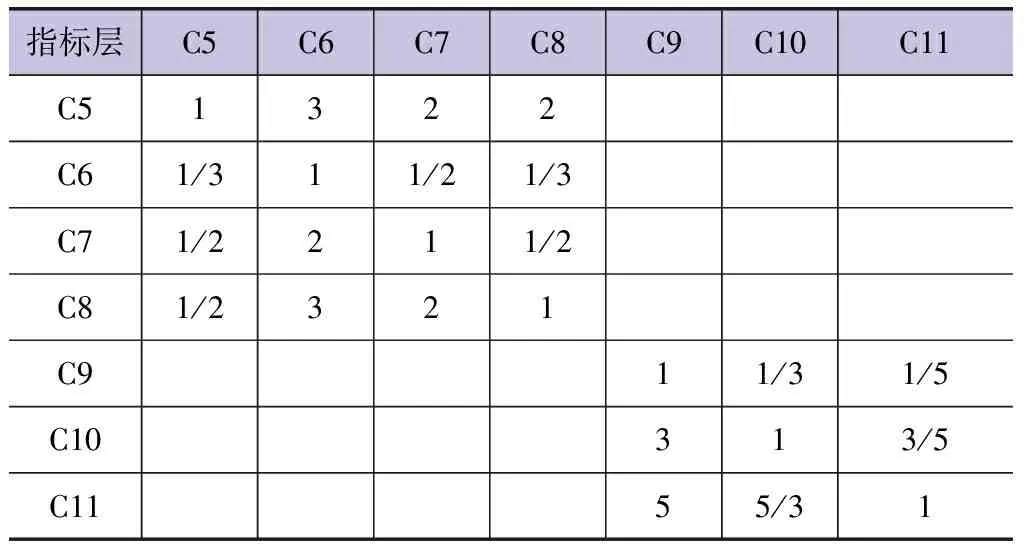
表6 B2-C判断矩阵

表7 B3-C判断矩阵

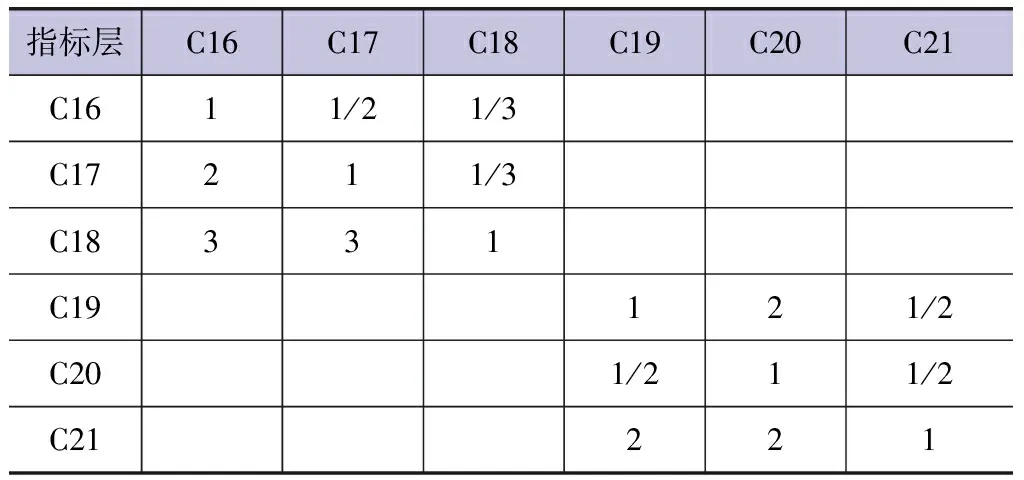
表8 B4-C判断矩阵

表9 阜新市水资源承载力评价指标体系主观权重及排序

3.5 客观权重计算

根据熵权法计算客观权重，运用MATLAB程序，得出客观权重，见表10。

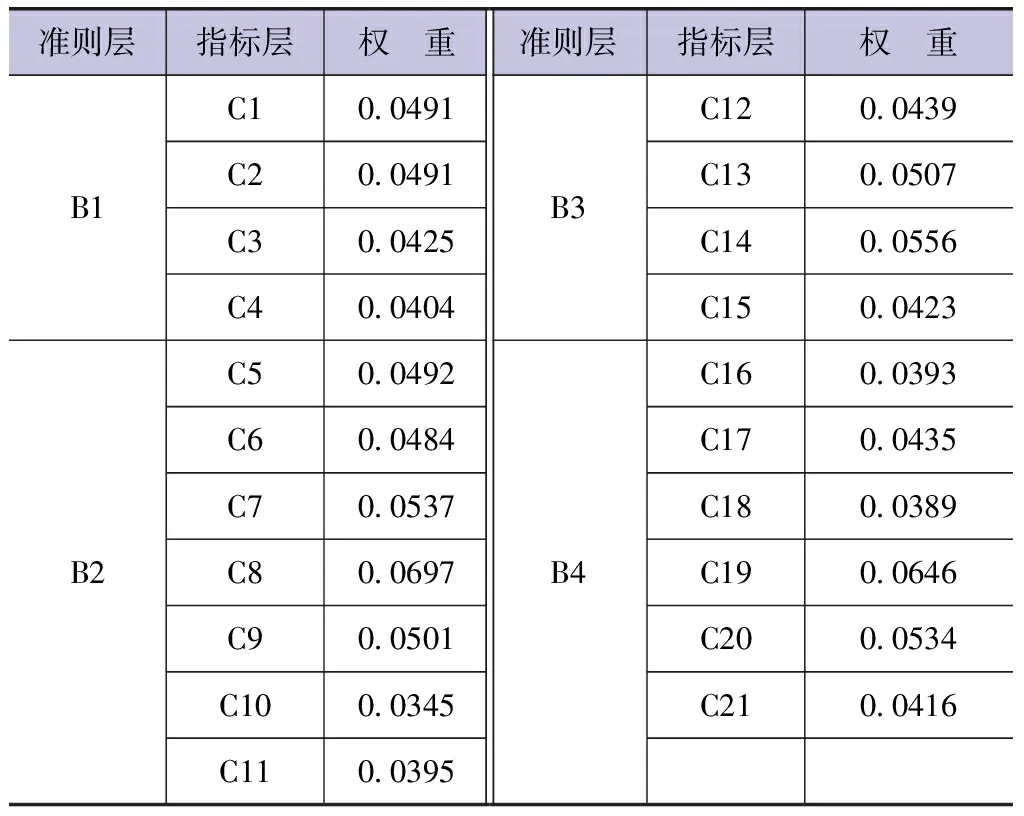
表10 阜新市水资源承载力评价指标体系客观权重

3.6 组合赋权计算

根据前面叙述的基于熵权法修正AHP法的组合赋权模型构建方法，求出组合权重，计算结果见表11。

表11 阜新市水资源承载力评价指标体系组合权重

4 综合评价结果

以阜新市的21个实测指标数列作为比较数列，根据参考数列和比较数列，参照式(10)计算两数列的绝对差和评价指标对5个等级的联系系数，结果见表12。

表12 阜新市水资源承载力指标数列与等级标准数列的联系系数

在计算出各指标关联系数的基础上，结合表11的组合权重求出综合关联度，同时将目标层、准则层和指标层的综合关联度列于表13，进行水资源承载力的详细分析。

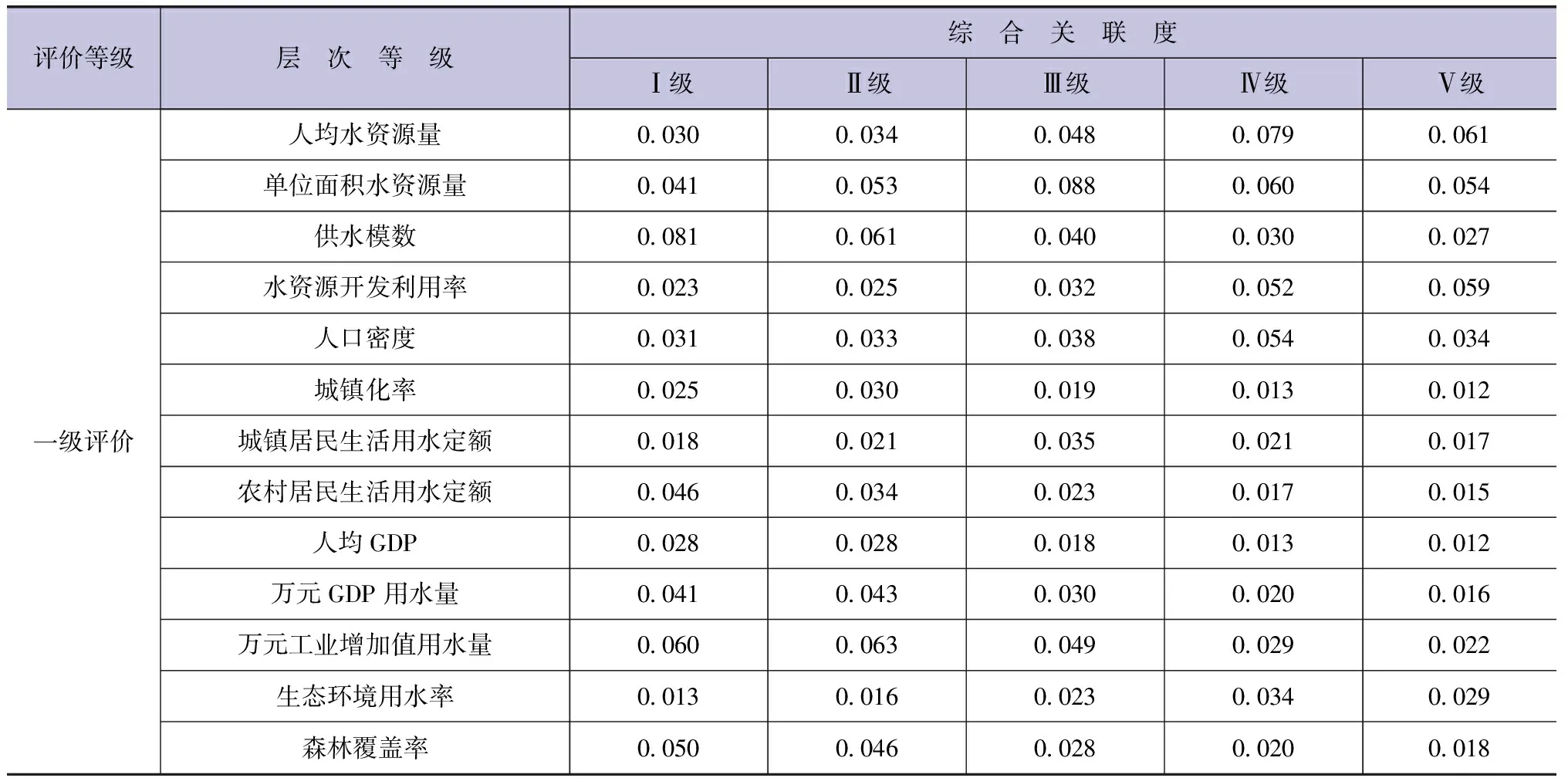
表13 阜新市水资源承载力综合评价结果

根据一级评价结果可知，处于Ⅴ级的有水资源开发利用率和地表水达标率，其Ⅴ级下综合关联度最高，说明阜新市的水资源开发利用率较高，地表水达标率水平较低；处于Ⅰ级的有供水模数、农村居民生活用水定额、森林覆盖率和城镇生活污水处理率，表明阜新市在这些方面比较有优势。

根据二级评价结果可知，阜新市水资源系统整体等级较差，这主要是由于阜新市水资源天然禀赋条件较差，人均水资源量少且水资源开发利用率较高；阜新市社会经济系统处于Ⅱ级，为较强承载水平，表明阜新市社会经济发展态势较为良好；阜新市生态环境系统处于Ⅳ级，这主要是由于生态环境用水率较低，地表水和地下水达标率较低造成的，生态环境系统的承载力较弱；阜新市水管理系统处于Ⅰ级，表明阜新市在水管理方面承载水平很强，实施最严格水资源管理制度有所成效。

根据三级评价结果，计算综合关联度可得R=[0.657，0.661，0.637，0.608，0.523]，结合最大关联度原则，阜新市水资源承载力综合评价的综合关联度为0.661，根据建立的水资源承载力评价标准，阜新市水资源承载力的总体水平属于Ⅱ级，承载力水平较高，符合阜新市实际情况。

5 结 语

本文从水资源、社会经济、生态环境、水管理4个层次选取21个指标构建水资源承载力综合评价指标体系，利用层次分析法确定不同准则层每个评价指标的重要性排序，然后根据熵权法确定的权重值计算相邻指标的重要性程度，依次求得每个指标的权重和准则层权重进而确定组合权重，这种组合形式可兼顾主观权重和客观权重的优点，提高单一权重方法的准确性。

水资源承载力综合评价是一个动态发展的系统，其评价标准会随着经济社会发展和科学技术的进步不断变化。本文在确定评价标准时主要参考国内外相关评价标准，力求科学地确立评价标准，但是受客观条件的影响，部分评价指标的评价标准还需进一步完善，以保证评价体系的与时俱进。