基于双层博弈的多臂在轨服务航天器路径规划*

2023-01-14高添吴云华张枭岳程斐

空间科学学报 2022年6期

高添吴云华张枭岳程斐

1(哈尔滨工业大学(深圳) 空间科学与应用技术研究院深圳 518055)

2(南京航空航天大学航天学院南京 211106)

0 引言

随着航天器在轨服务技术的飞速发展，空间机械臂和装配有空间机械臂的航天器已成为空间在轨操作的主要对象，将承担在轨装配、维修、燃油加注、运输和空间碎片清理等诸多工作[1,2]。在轨操控作业中，机械臂的运动规划和控制始终是研究的热点，例如在笛卡尔空间进行空间机械臂点对点的规划[3,4]等。随着在轨操控任务复杂性的提升，如在轨灵巧操作、移动爬行等，未来操控任务均要求空间机械臂能多臂协同地开展工作，例如蜘蛛制造（SpiderFab）[5]等。这类任务除了要求航天器各机械臂实现精确的位置控制外，还要保证各臂自身和相互之间不发生碰撞。因此，考虑自避障的多臂路径规划是实现精准在轨操控的前提和基础。

目前，针对机械臂路径规划及避障问题的研究有多种方法。Warren等[6,7]提出利用人工势场法（Artificial Potential Field，APF）实现机械臂避障，该方法能快速有效地提供安全避障路径，但是易陷入局部最小点处。Riky等[8]改进人工势场算法，通过建立辅助函数求解局部极小值问题。Bohlin等[9]提出概率路线规划（Probabilistic Roadmap Planners，PRMs）方法，通过最小化规划期间执行的碰撞检查次数，达到最小化规划运行时间的目的。Jia等[10]提出一种利用A-star 算法在机械臂的自由运动空间进行路径搜索，从而实现机械臂无碰撞路径规划的方法。Duchoň等[11]对A-star 算法在计算时间和路径优化方面进行一些改进。Yao等[12]也对传统A-star 算法进行评价函数加权处理的改进，同时引入人工搜索标记，可以有效快速摆脱障碍陷阱。上述方法多适用于单机械臂路径规划及避障等情形，针对多机械臂的研究较少。

与传统单机械臂仅考虑路径规划及过程中实现外部避障的目标有所不同，多机械臂还需要考虑各条臂之间的协同规划以及自身避障，特别是动态环境下的规划与自避障。针对多机械臂的路径规划问题，可考虑将各臂看成智能体，通过博弈算法等智能策略进行设计。Guo等[13]利用博弈原理改进Q-Learning 算法进行智能体的避障协作路径规划。Shen等[14]提出一种博弈论数据融合辅助算法用于无人机在对抗环境中的协作和智能路径规划。Lee等[15]将混合博弈策略用于多目标进化算法，应用于无人机系统任务路径规划。目前，关于博弈论应用于机械臂路径规划的算法还较少。Wang等[16]提出一种基于博弈的快速拓展随机树（Rapidly-exploring Random Tree，RRT）算法，将博弈论用于寻找随机树的新网格。该方法仅考虑单机械臂路径规划，不适用于多机械臂自避障约束下的路径协同规划。

为解决多臂航天器的智能规划问题，本文从多机械臂协同围捕任务出发，同时考虑围捕过程中各机械臂的避障问题，提出一种基于双层博弈的多机械臂路径规划方法。本文给定了多臂航天器的基本构型及建立的多机械臂运动学模型；在博弈原理的基础上建立了多机械臂的博弈模型，通过机械臂末端追踪目标的博弈实现对目标的围捕，同时在围捕过程中嵌套肘关节博弈实现避障，通过双层博弈实现多条机械臂之间的协同规划；给出了双层博弈的基本算法流程及其纳什均衡解的求解策略；对多机械臂围捕案例进行仿真分析，验证了所提出算法在末端精确跟踪和肘部避障方面的有效性和实用性。

1 模型及数学原理

1.1 机械臂模型

研究的多臂航天器由一个基座和四条相同的仿人型7-DOF 机械臂组成，机械臂均匀分布在基座四周，其中第1，2，3 关节构成肩关节，第4 关节为肘关节，第5，6，7 关节构成腕关节。利用标准D-H（Denavit-Hartenberg）参数化方法建立机械臂模型，多臂航天器整体构型以及各臂DH 坐标系如图1 所示。单臂连杆参数列于表1。

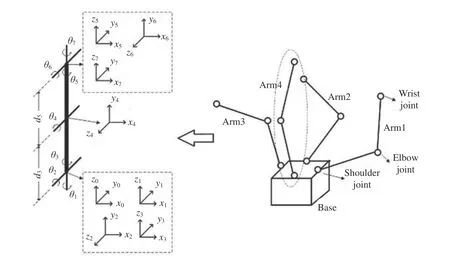
图1 多臂航天器整体构型及坐标系定义Fig.1 Configuration of the multi-arm spacecraft and the definition of the coordinates

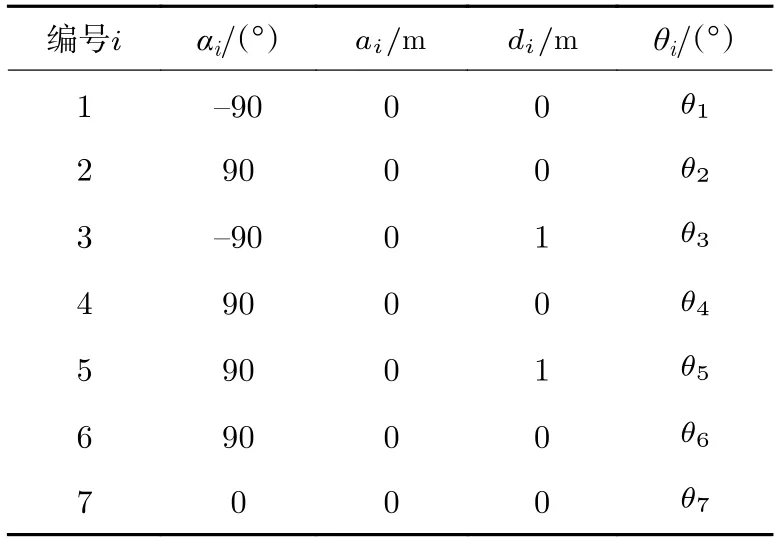
表1 机械臂DH 参数Table 1 DH parameters of the manipulator

针对该仿人型7-DOF 机械臂，定义其基座点B与肩关节点S之间的连线和末端腕关节点W形成的平面为参考平面，其肩关节点S，肘关节点E和腕关节点W形成的平面为臂平面，定义臂平面和参考平面之间的夹角为臂型角φ[17]，机械臂臂型角示意如图2 所示。由此得知，在给定末端位姿的情况下，仿人型机械臂的臂平面可以绕SW运动，臂型角的相关应用将在1.3 节阐述。

图2 机械臂臂型角Fig.2 Arm angle of manipulator

1.2 博弈原理

博弈论是研究多个具备进行决策的行为主体在相互作用时，如何选择合适的决策以达到总体收益最大的方法，也即达到一种均衡状态，称之为纳什均衡。其中，具备决策行为的主体为博弈方，主体所选择的决策形成的组合称之为策略集。根据已制定的收益数学模型，对策略集里的任一组合均能求得一组收益值，其组成的集合称之为收益集。通过对收益集求纳什均衡解得到的一组策略组合即为本次博弈中各博弈方所采取的最佳决策。

综上所述，博弈过程可以描述如下。

（1）假设共有n个博弈方参与博弈，记为p1，p2，...，pn，每个博弈方可供选择的策略集分别为S1，S2，...，Sn，每个策略集内的可选择策略数量分别为n1，n2，...，nn。

（2）假设各博弈方在本次博弈中所采取策略为s1∈S1，s2∈S，...，sn∈Sn。

（3）根据制定的收益数学模型得到博弈方采取的一组策略对应的一组收益(r1，r2，...，rn)=f(s1，s2，...，sn)，所有的收益组合形成收益集R，对收益集R求得纳什均衡解，记作

其中，sij表示第i个博弈方选择对应策略集里的第j个策略。易知，纳什均衡解存在唯一解、多解以及无解的情况。

当存在唯一解时，可知此时该唯一解即为本次博弈各方采取的最优策略。

当无解时，此时博弈无法达到均衡，无法保证取得最大收益。为了求得一组策略使得总体收益不至于最差，因此采用max-min 原则进行选取，对于任意s1∈S1，...，si-1∈Si-1，si+1∈Si+1，...，sn∈Sn，满足

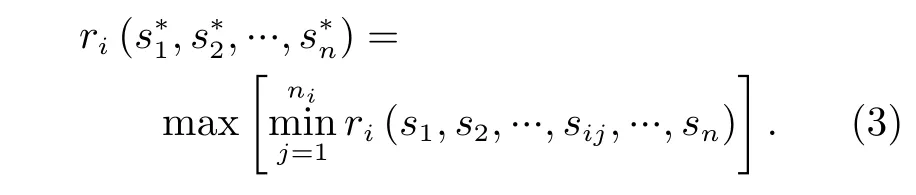
1.3 多机械臂双层博弈模型

在机械臂模型和博弈理论基础上给出多机械臂航天器的双层博弈模型。多臂航天器的四条仿人型机械臂分别为四个博弈方。为简化模型的复杂程度，将机械臂工作空间栅格化，机械臂末端轨迹视为离散点，机械臂末端的运动视为点到点之间的直线运动。易知，从当前一点运动到下一点共有18 个方向可供选择，如图3 所示，加上停止运动共19 个策略，即构成了各条机械臂追捕博弈的策略集。

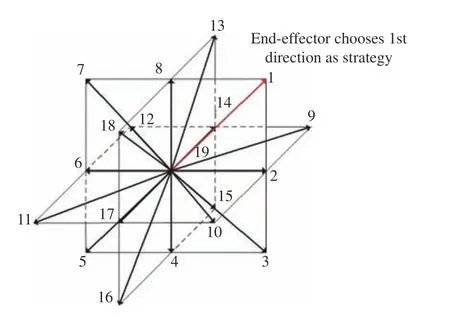
图3 由19 个可能动作构成的机械臂追捕博弈策略集Fig.3 Strategy set of the manipulator tracking game formed by the 19 potential actions

为评估各机械臂所选择策略的优劣，引入收益数学模型，构建策略集对应的收益集。收益函数可表示如下：

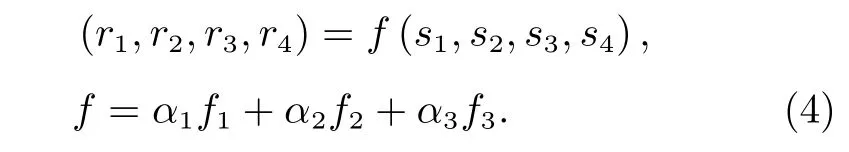
其中，f1为评价各机械臂末端与目标距离的收益函数，f2为评价各机械臂末端之间避障的收益函数，f3为评价各机械臂末端围捕中心与目标距离的收益函数；α1,α2,α3为权重系数。

定义评价各机械臂末端与目标距离收益函数f1如下：

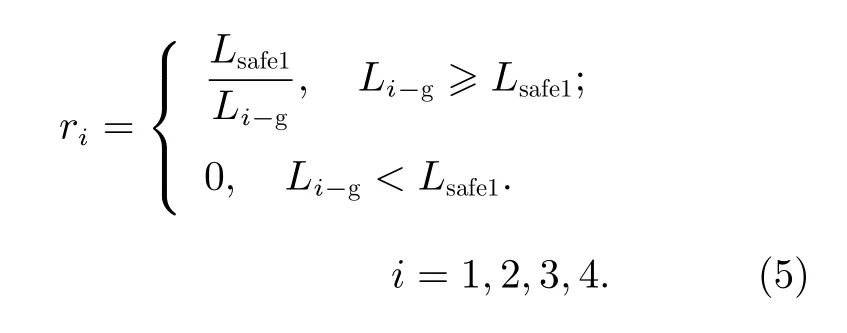
其中，Lsafe1为机械臂末端与目标之间的安全距离，Li-g为第i条机械臂与目标之间的距离。

定义评价各机械臂末端之间避障的收益函数f2如下：

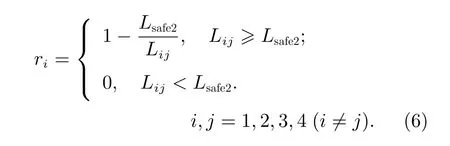
其中，Lsafe2为各机械臂末端之间的安全距离，Lij为第i条机械臂末端与第j条机械臂末端之间距离的最小值。

定义评价各机械臂末端围捕中心与目标距离的收益函数f3如下：

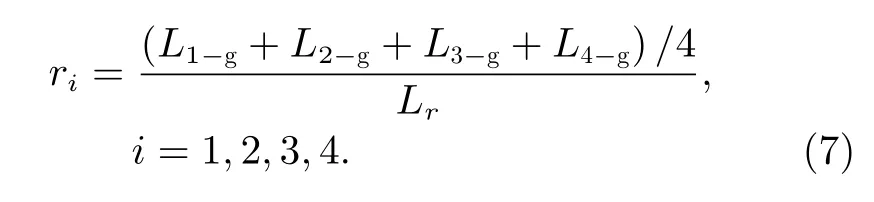
其中，(L1-g+L2-g+L3-g+L4-g)/4 为各机械臂末端形成的四边形中心与目标的距离，Lr为中心到目标的收益参考距离。

值得注意，安全距离Lsafe1、Lsafe2、参考收益距离Lr及各项分收益占总收益的比例α1，α2，α3均为常数，具体数值由末端离散点之间的步长决定，在此不做深入研究。

在完成多机械臂末端追捕目标博弈后，考虑多机械臂在运动过程中可能发生臂与臂之间的碰撞，增加肘关节之间的避障博弈，考虑在机械臂末端位姿不变的情况下，机械臂的肘关节点E可以绕肩关节点S和腕关节点W之间的连线旋转，旋转角度φ即为臂型角，因此，定义机械臂的臂型角为肘关节避障博弈的策略集。同理，构建机械臂肘关节避障博弈的收益集，收益函数表示如下：

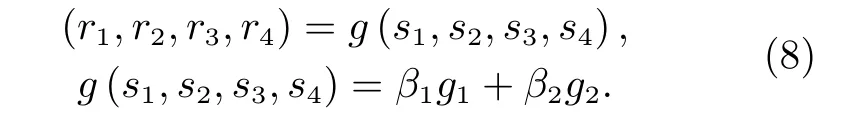
其中，g1为评价各机械臂肘关节之间距离的收益函数，g2为评价各机械臂肘关节之间均匀分布的收益函数。β1和β2为权重系数。

定义评价各机械臂肘关节之间距离的收益函数g1如下：

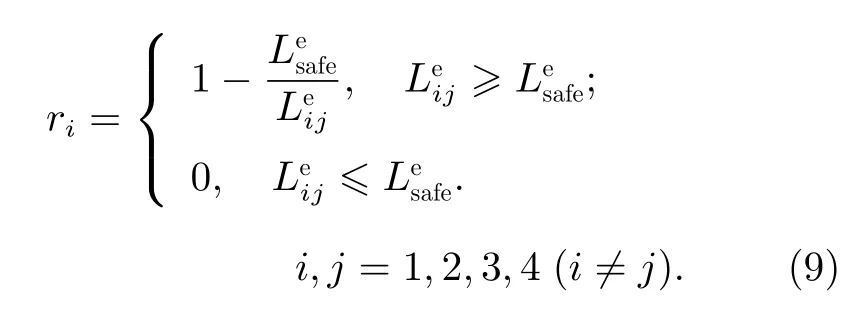
定义评价各机械臂肘关节之间均匀分布的收益函数g2如下：

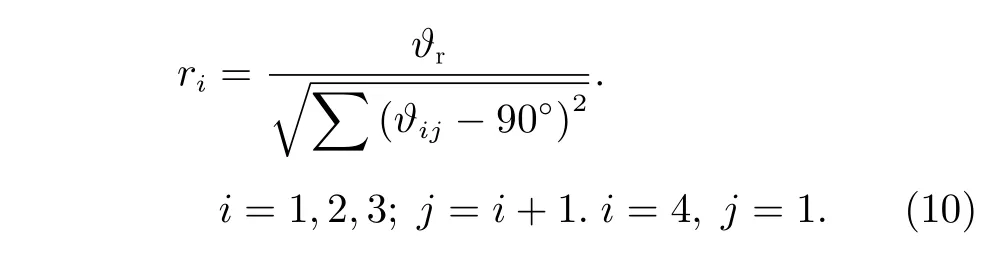
其中，ϑr为机械臂肘关节均匀分布参考收益角度，θitoj为第i条机械臂肘关节与第j条机械臂肘关节之间在水平面投影的对心夹角。机械臂肘关节对心夹角如图4所示。

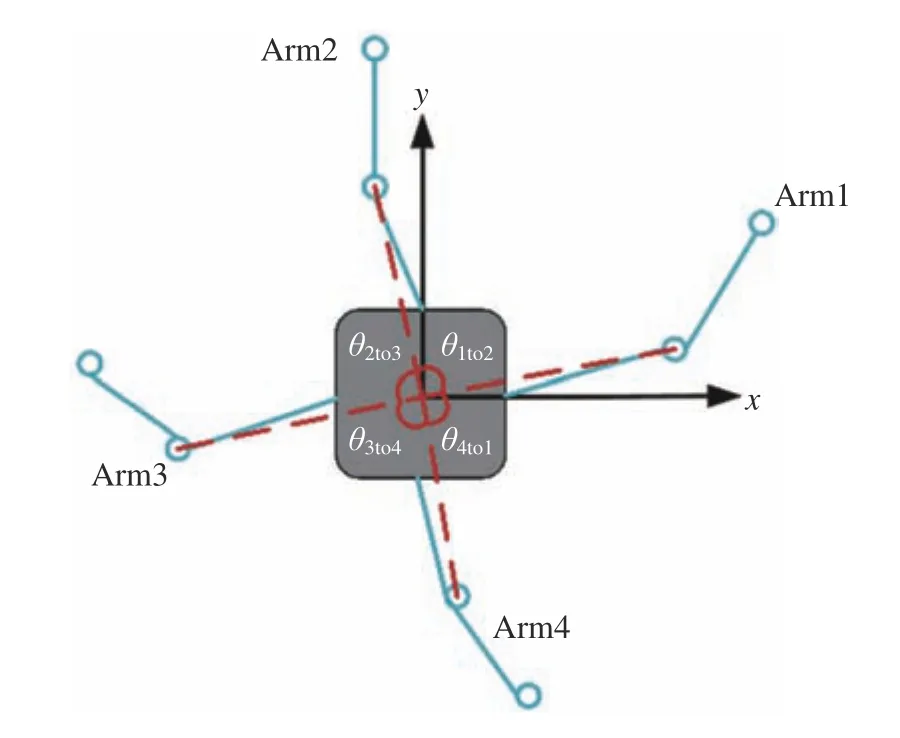
图4 机械臂肘关节对心夹角Fig.4 Angle against the center of manipulator’s elbow joint

同样，肘关节避障博弈收益模型中的安全距离，参考收益角度ϑr和各项分收益所占比例β1，β2均为常数，具体数值由臂型角变化范围决定。

在机械臂实际运动过程中，考虑机械臂末端运动速度不能突变，以及机械臂臂型角度不能突变，由此引入约束集对策略集加以约束。假定某一机械臂在上一步博弈中末端运动方向为D0，在本次博弈中运动方向为D；在上一步博弈中臂型角为φ0，在本次博弈中臂型角为φ。则由最优化理论，博弈问题可以描述为

其中，C为臂型角不引起突变的阈值。

同时考虑到机械臂末端为离散点之间的直线运动，为保证末端运动性能，对末端进行梯形速度曲线的直线运动规划。

2 博弈问题求解

2.1 博弈算法流程

将单步博弈拓展至连续博弈，同时为提高算法的效率，增加肘关节碰撞检测算法，即各机械臂在进行末端追捕博弈时，检测当各肘关节之间距离在碰撞安全阈值内时，才执行肘关节避障博弈。由此得到多臂航天器双层博弈算法流程如下。

（1）设定博弈初始场景，生成栅格模型，初始化各机械臂构型，随机生成追捕目标位置。

（2）由各机械臂末端与目标之间的相对位置判断是否捕获成功（条件为某一机械臂末端与目标距离保持在给定捕获范围内）。若捕获成功，则博弈结束，反之执行（3）。

（3）由各机械臂肘关节相对位置判断是否需要执行避障博弈（条件为各机械臂肘关节之间距离在碰撞安全阈值内）。若判断需要，则执行（8），反之执行（4）。

（4）分析各机械臂末端当前约束，得到下一步各机械臂末端可选择策略，形成末端策略集。

（5）根据式（4）的收益数学模型计算得到末端策略集对应的末端收益集。

（6）对末端收益集求取纳什均衡解，得到各机械臂末端下一步最优策略组合。

（7）各机械臂执行该策略组合运动到下一步，并转到（2）判断捕获是否成功。

（8）分析各机械臂末端和肘关节当前约束，得到下一步各机械臂末端和肘关节可选择策略，形成末端和肘关节策略集。

（9）根据式（4）和式（8）的收益数学模型计算得到末端和肘关节策略集对应的末端和肘关节收益集。

（10）对末端和肘关节收益集分别求取纳什均衡解，得到各机械臂末端和肘关节下一步最优策略组合。

（11）各机械臂执行该策略组合运动到下一步，并转到（2）判断捕获是否成功。

如此，完成机械臂追捕目标和肘关节避障双层博弈策略，机械臂双层博弈流程如图5 所示。

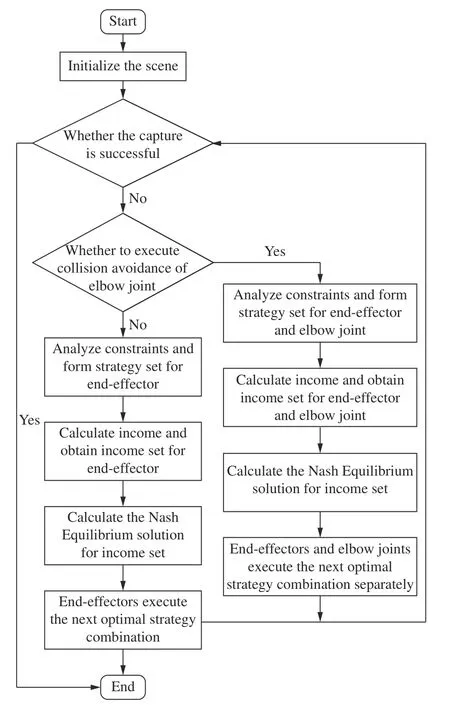
图5 双层博弈算法流程Fig.5 Flow chart of the two-level game algorithm

2.2 纳什均衡求解算法

在给出纳什均衡解满足的数学表达后，以四方博弈为例，给出求取纳什均衡解的完整算法如下。

算法1 纳什均衡求解算法

由此，针对多机械臂博弈模型，结合多机械臂双层博弈算法及多机械臂末端追捕博弈和肘关节博弈的纳什均衡解求解策略，即可得到所需的机械臂路径规划结果。

3 仿真分析

为验证上述双层博弈算法的有效性和实用性，对提出的模型和算法进行仿真分析。以仿人型7-DOF多机械臂为研究对象，设定博弈场景空间范围为5 m×5 m×5 m，假定多臂航天器能进行精确的姿态位置控制，各机械臂根部的空间位置坐标以及初始构型关节角见表2。

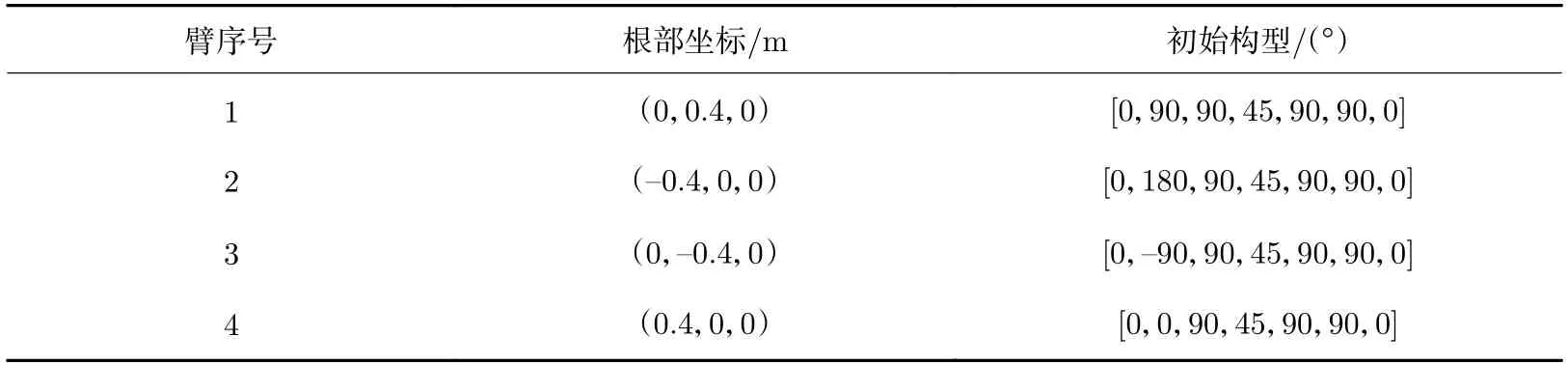
表2 机械臂仿真初始参数Table 2 Initial parameters of the simulation

3.1 机械臂末端追捕博弈仿真

按照多机械臂末端追捕博弈算法对机械臂末端追捕目标的博弈行为进行仿真，得到机械臂末端追捕博弈轨迹如图6 所示，其中机械臂末端到目标的距离变化如图7 所示。从图6 可看出，各机械臂末端对于移动的被追捕目标均能表现出有效的追捕。

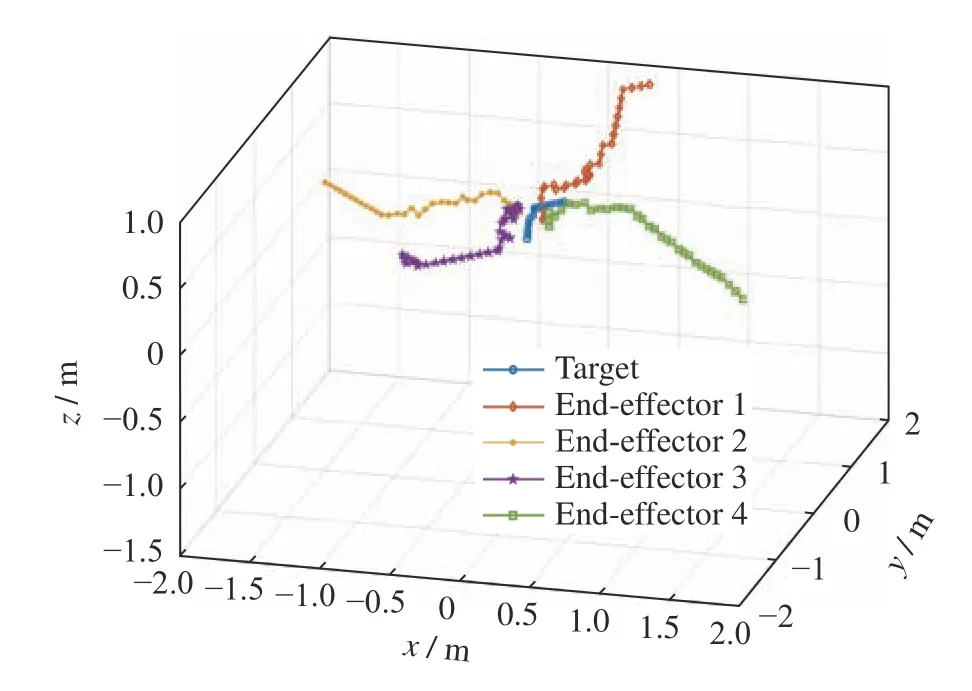
图6 机械臂末端追捕博弈轨迹Fig.6 Trajectory diagram of the end effector in the hunting game

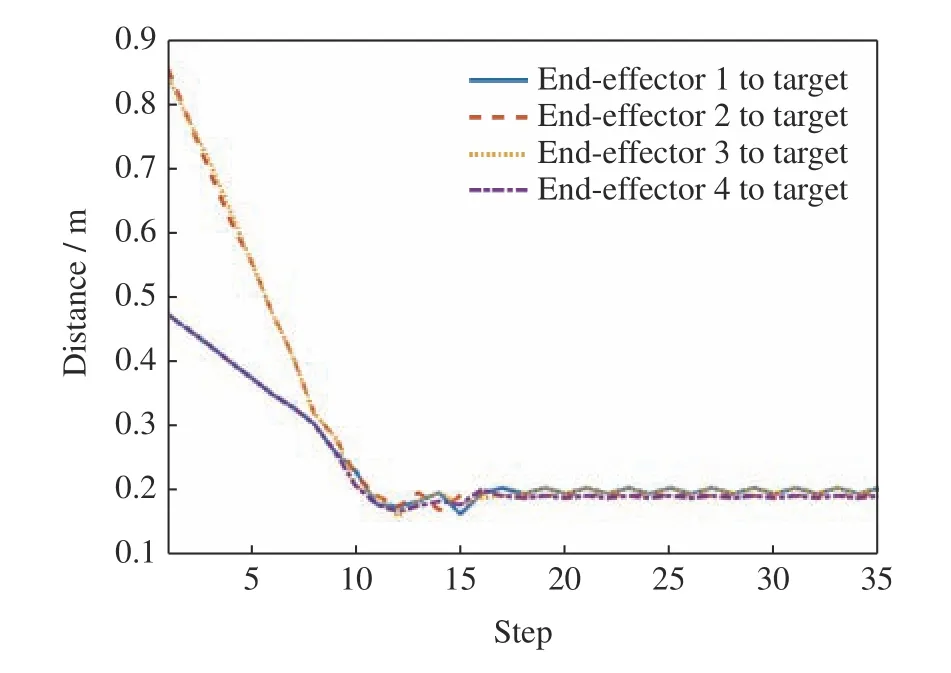
图7 机械臂末端至目标的距离Fig.7 Distance between multi-manipulator end-effectors and target

3.2 机械臂双层博弈仿真

按照多机械臂末端追捕和肘关节避障双层博弈算法进行机械臂双层博弈全过程仿真实验，截取的部分机械臂博弈行为如图8 所示。

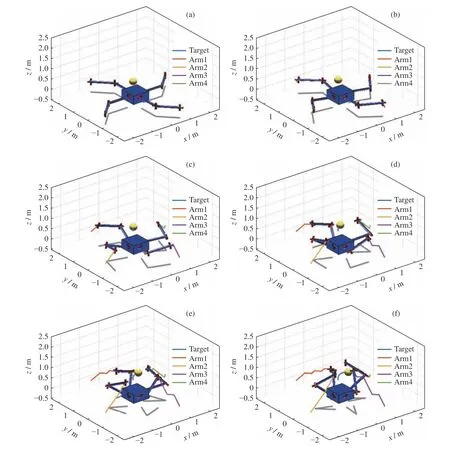
图8 部分机械臂双层博弈行为Fig.8 Partial schematic diagram of the manipulators in the two-level game

从图中可以看出，机械臂在双层博弈下末端可以快速准确地接近运动目标进行追捕，同时肘关节运动能够保证避障，臂与臂之间相对于基座的空间分布较为均匀。为了说明均匀性问题，分别提取在有无肘关节避障博弈情况下各机械臂肘关节之间在水平面投影的对心夹角进行对比分析，如图9 所示。从图9 可看出，无肘关节避障博弈时，各机械臂肘关节之间对心夹角随着博弈的进行呈发散状态；在增加肘关节避障博弈之后，各机械臂肘关节之间对心夹角均能保持在9 0°±10°范围内，肘关节分布均匀性良好。