浅层平板载荷试验变形模量计算公式推导

刘秀军

（1. 深圳市勘察测绘院（集团）有限公司，广东 深圳 518028；2. 中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州 221116）

0 引 言

岩土材料的变形模量是岩土工程计算分析中的一个重要的力学参数，尤其在地基的变形与沉降计算中起到举足轻重的作用[1]。岩土材料的变形模量可采用多种方法求得，例如：（1）由原位平板载荷试验结果求出；（2）通过理论计算公式由室内试验获得的压缩模量换算得出；（3）用三轴试验反复加卸荷求出。据文献[2]研究，虽然平板载荷试验的结果会受到基础性状和尺寸等因素影响，但比较符合实际力学边界条件，加之后两种方法由于受取样扰动影响，其结果严重偏低，因此目前岩土的变形模量主要通过原位平板载荷试验的结果计算求得。据相关规范[3-6]，土的变形模量应根据p-s曲线的初始直线段，按均质各向同性半无限弹性介质的弹性理论计算。浅层平板载荷试验的变形模量E0，可按下式计算：

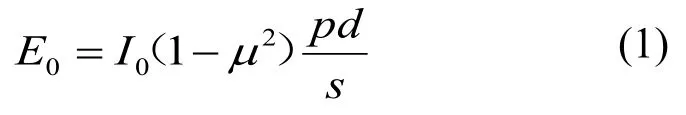
式中：I0为刚性承压板的形状系数，圆形承压板取0.785，方形承压板取0.886；μ为土的泊松比；d为承压板直径或边长；p为p-s曲线线性段的压力；s为与p对应的沉降。

然而，式（1）如何而来？相关规范提供的刚性承压板形状系数的具体数值如何确定出来？笔者查阅相关文献后均未能找出较为详尽的解答。因此有必要对浅层平板载荷试验变形模量的计算公式进行系统的推导和阐述，并从理论的角度计算出刚性承压板的形状系数。

1 Boussinesq弹性理论位移解

如图1所示，据文献[7]，在不计体力的均质半无限弹性体表面作用一法向集中力Q，则半无限体内任意点M（x,y,z）处的竖向位移为：

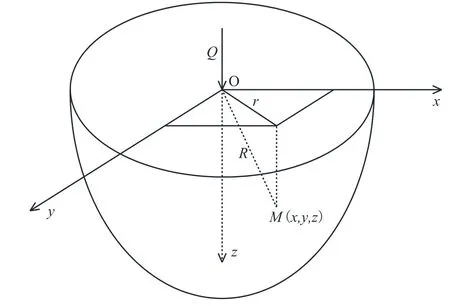
图1 Boussinesq解示意图Fig. 1 Schematic diagram of the Boussinesq solution

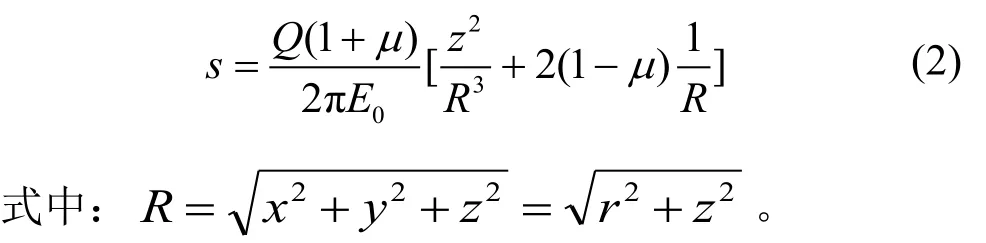
从式（2）可以看出，在空间体表面（z=0）上某一点（r,0）处的竖向位移为：

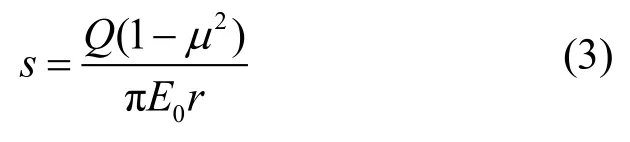
2 圆形垂直均布荷载下的位移解

如图2所示，在均质半无限弹性体表面上，一半径为a的圆面积内均布法向荷载p，求取荷载作用面积下深度z处M点的沉降。取微分面积dA= ρdψdρ ，如图中阴影线所示，由式（2）可得M点的沉降为：

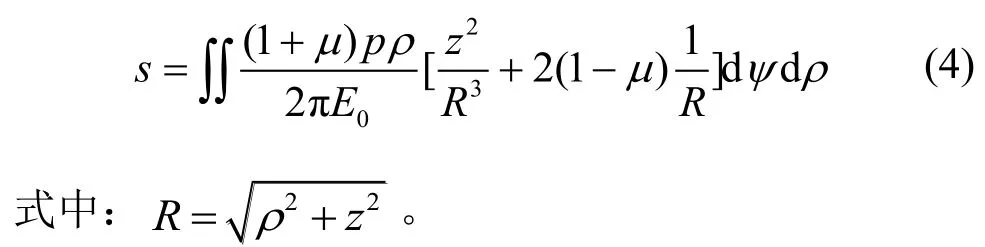
图2 圆形面积计算示意图Fig. 2 Schematic diagram of the circular area calculation

在荷载作用区域内，r由0变化到a，ψ由0变化到π，ρ由0变化到mn，且mn= 2acosθ，考虑对称性，所以有：

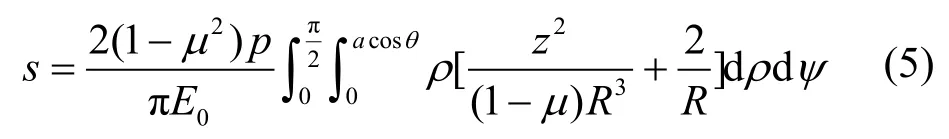
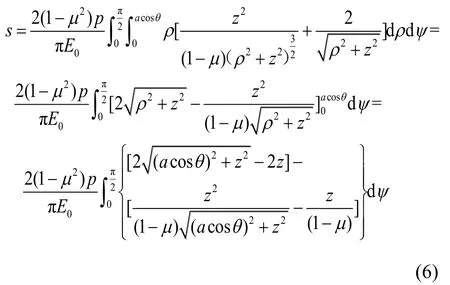
上式即为圆形垂直均布荷载下的弹性理论竖向位移解。下面来分析几种特殊情况：

（1）表面沉降（z=0时）

则上式简化为：

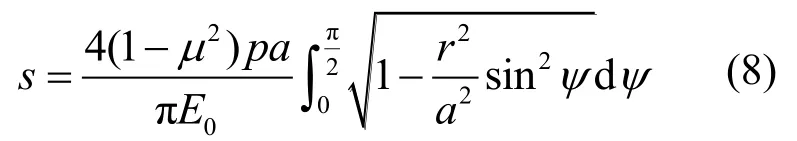
在上式中，令r=0，则得到圆心处的沉降：

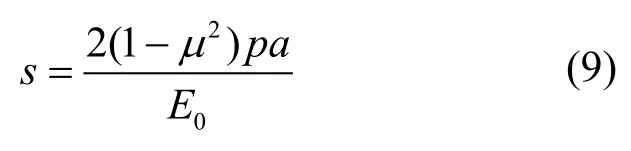
令r=a，则得到荷载圆边界处的沉降：

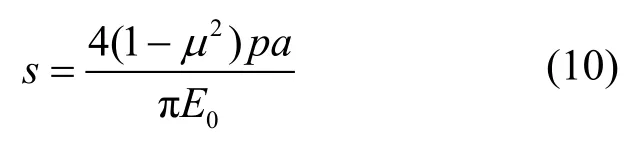
对比式（9）和式（10），可知最大沉降发生在圆心处，最小沉降发生在荷载圆边界处，且圆心处的沉降为荷载圆边界处沉降的倍。

（2）荷载圆中心轴线上的沉降（r=0时）

则式（7）化为：

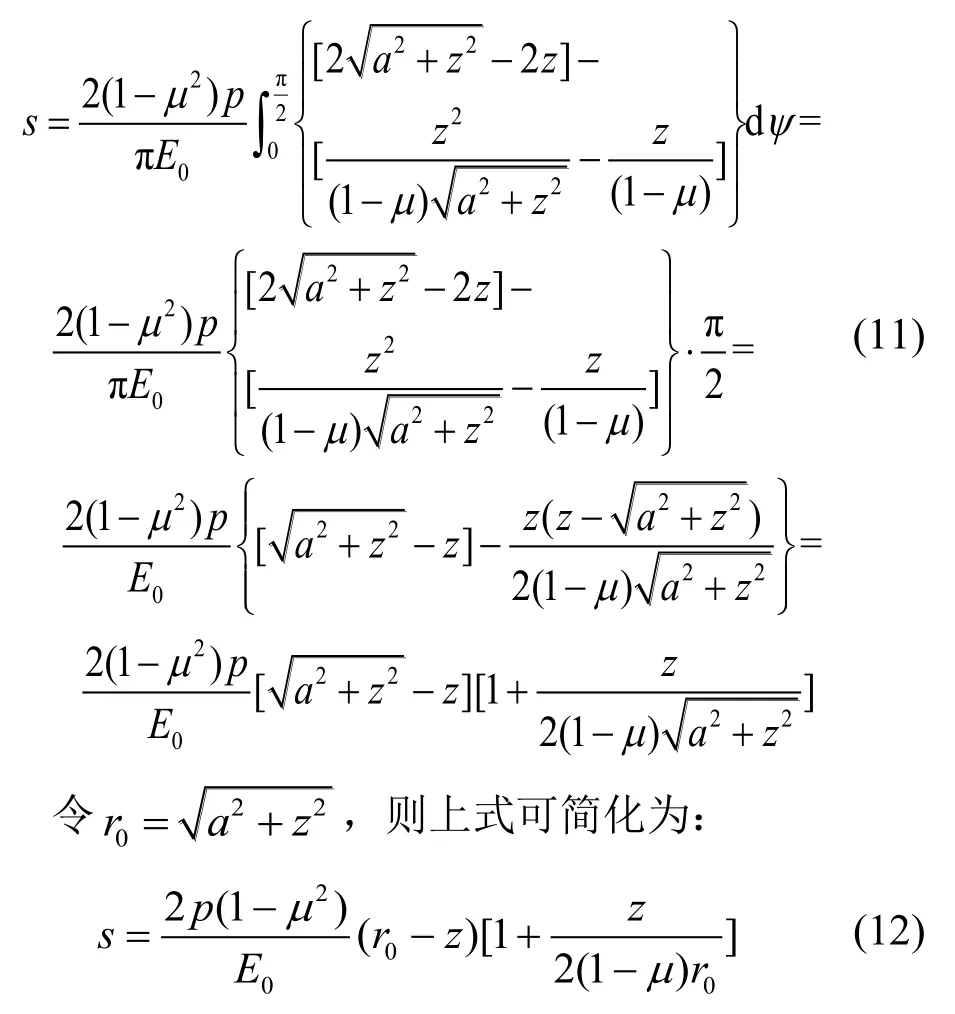
上式即为圆形垂直均布荷载下中轴线上深度z处的竖向位移解，与文献[8]给出的公式相同。当z=0时，上式可变为式（9），即：

式中：d为圆形垂直均布荷载的直径。

将式（13）变换形式后可得：

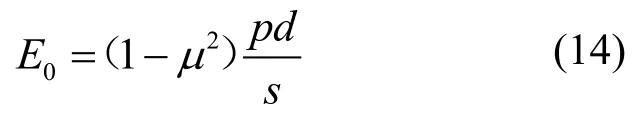
由此可见，将式（14）乘以系数I0即可得到式（1）。

（3）荷载圆边界线下的沉降（r=a时）

则式（7）化为：

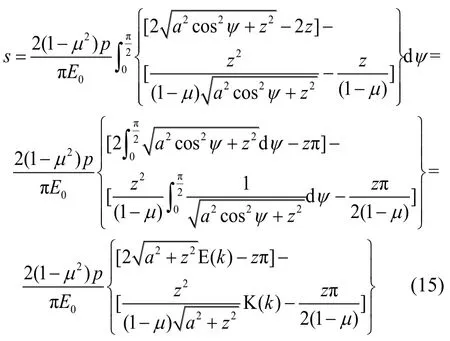
式中：E(k)为第二类完全椭圆积分，即：

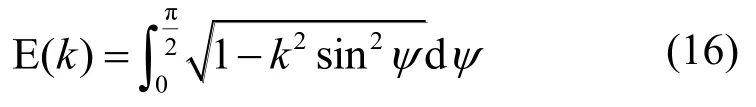
K(k)为第一类完全椭圆积分，即：

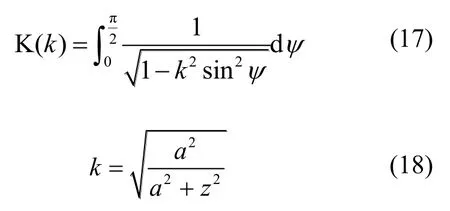
式（15）即为圆形垂直均布荷载的边界线下深度z处的竖向位移解，当z=0时，式（15）可变为式（10）。

3 方形垂直均布荷载下的位移解

如图3所示，在均质半无限弹性体表面上，一边长为l×b的方形面积内均布法向荷载p，求取荷载作用面积下深度z处M点的沉降。取微分面积dA=dxdy，如图中阴影线所示，由式（2）可得M点的沉降为：

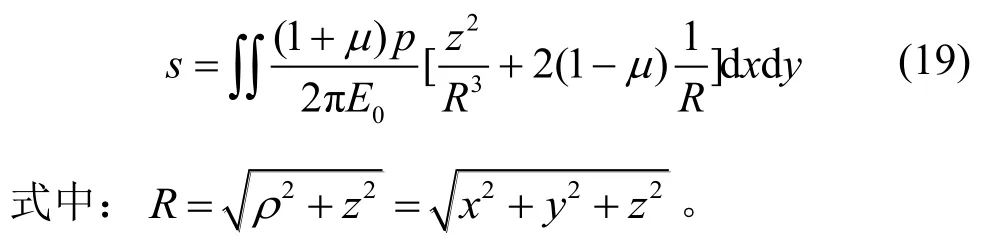
图3 方形面积计算示意图Fig. 3 Schematic diagram of the square area calculation

在荷载作用区域内，x由0变化到l，y由0变化到b，考虑对称性，则在方形面积角点下深度z处的沉降如下：

对上式中的被积公式分别积分如下：

式（21）在y=0处的泰勒展开式为：

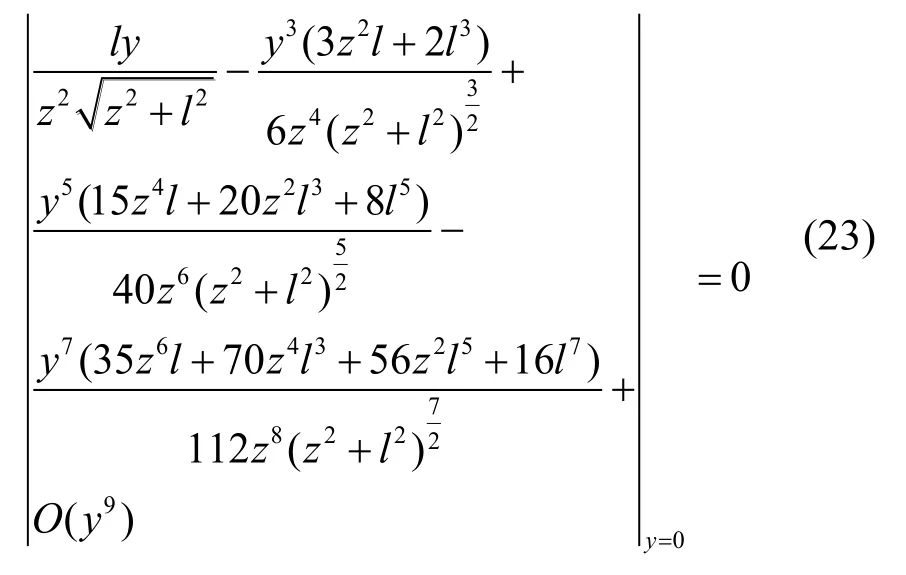
式（22）在y=0处的泰勒展开式为：

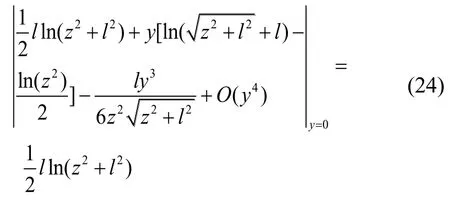
因此，可知：

将式（25）和式（26）代入式（20），得：

上式即为方形垂直均布荷载下方形面积角点下深度z处的沉降，与文献[8]给出的公式相同。

由此可知，方形面积中心点下深度z处的沉降为：

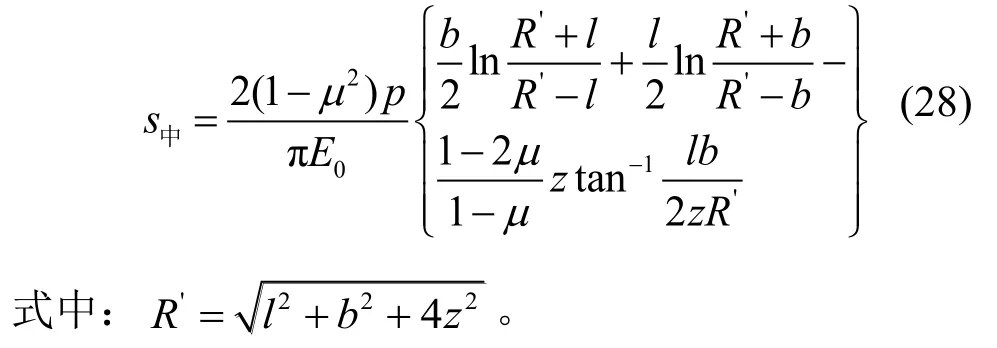
x方向边长中心点下深度z处的沉降为：

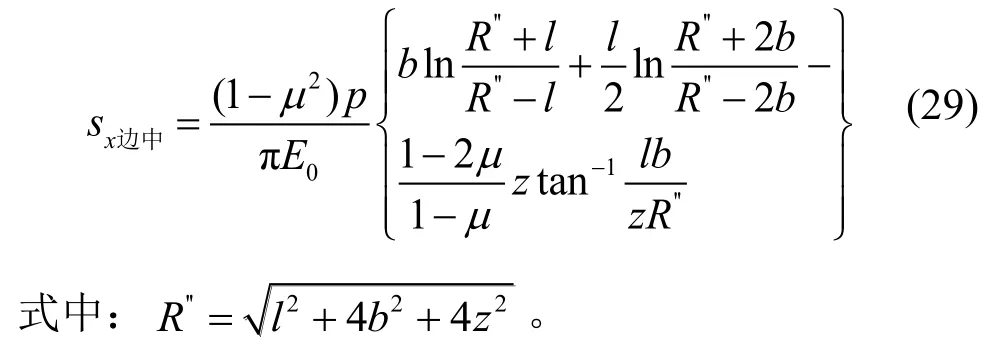
y方向边长中心点下深度z处的沉降为：

下面来分析几种特殊情况：

（1）正方形荷载面积（l=b时）

式（27）简化为：

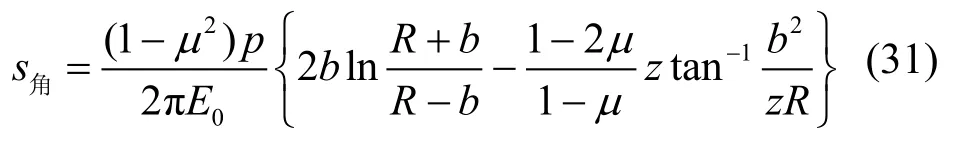
式（28）简化为：

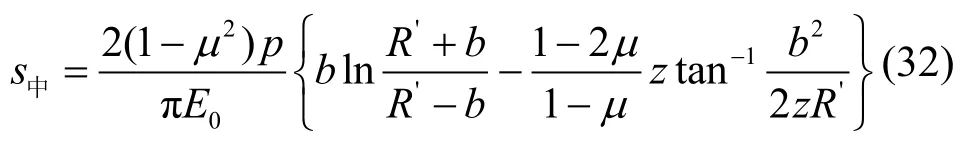
式（29）和式（30）简化为：

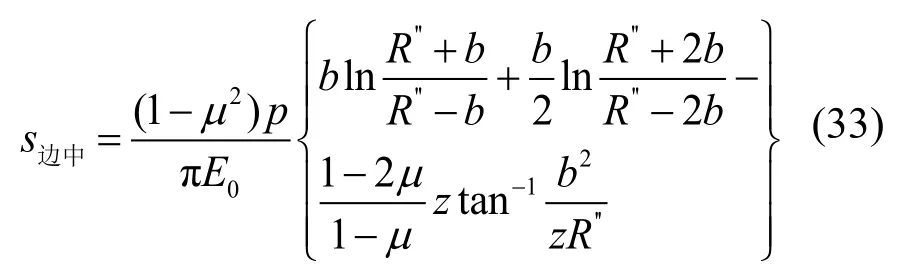
（2）正方形荷载面积表面沉降（z=0时）

式（31）简化为：

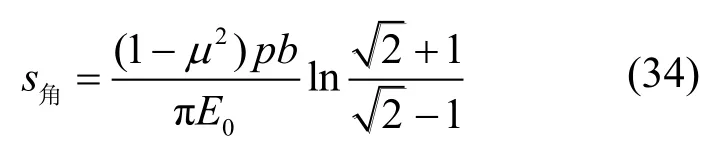
式（32）简化为：

式（33）简化为：

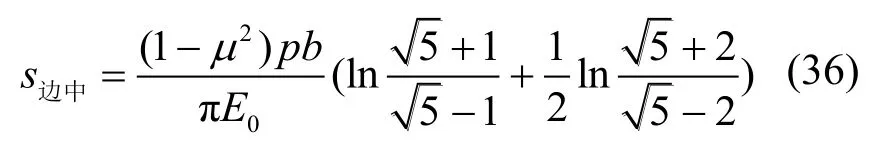
对比式（34）～（36）可知，正方形荷载中心处的表面沉降为角点处表面沉降的2倍，荷载边界中心处的表面沉降约为角点处表面沉降的1.79倍。

4 刚性承压板形状系数I0

前述圆形和方形荷载作用面积实际上为柔性作用面积，而在浅层平板载荷试验中，由于承压板相比岩土体为刚性体，因此承压板其下各点的沉降理论上均相等。根据FOX[9]的著名论点：竖向荷载作用在刚性面积上所产生的竖向位移可以用相当的均匀荷载作用在形状相同的柔性面积上所引起的平均竖向位移来近似计算。DAVIS等[10]和POULOS等[11]引用了竖向荷载作用在刚性面积上所产生的竖向位移的近似计算公式如下：

圆形和长条形：

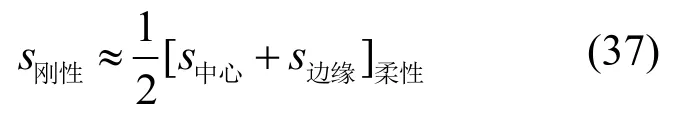
矩形：

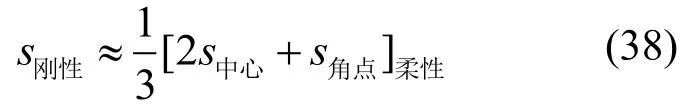
将式（9）和式（10）代入式（37）可得圆形刚性承压板下的平均竖向位移为：

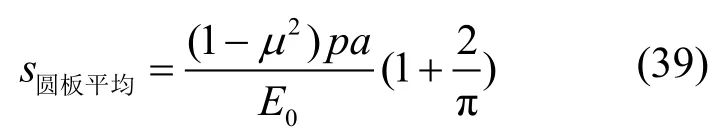
据上式可反算得到圆形刚性承压板下的平均变形模量为：

将式（34）和式（35）代入式（38）可得方形刚性承压板下的平均竖向位移为：

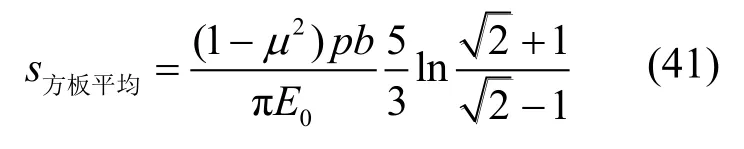
据上式可反算得到方形刚性承压板下的平均变形模量为：

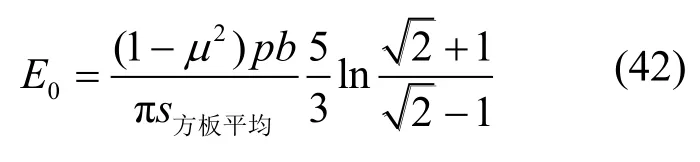
将式（40）与式（1）作对比可得圆形刚性承压板的形状系数为：

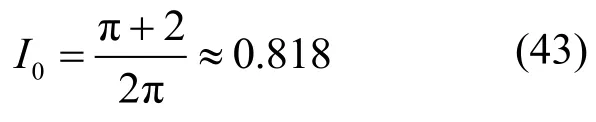
将式（42）与式（1）作对比可得方形刚性承压板的形状系数为：

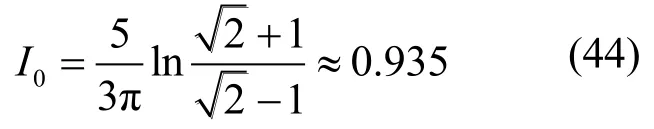
由此可知，由Boussinesq弹性理论竖向位移解推导出的圆形刚性承压板形状系数约为 0.818，略大于相关规范提供的 0.785，推导出的方形刚性承压板形状系数约为 0.935，略大于相关规范提供的0.886，虽然对计算结果影响不是很大，但从原理上却更为清晰合理一些。

5 结 论

岩土材料的变形模量是岩土工程力学分析中的一个重要的参数，目前主要通过原位平板载荷试验的结果计算求得。本文基于Boussinesq弹性理论位移解，对相关文献中由浅层平板载荷试验结果计算变形模量E0的公式以及刚性承压板的形状系数I0进行了系统的推导和阐述，得出以下结论：

（1）浅层平板载荷试验变形模量的计算公式实际上是在Boussinesq弹性理论竖向位移解的基础上乘了一个刚性承压板的形状系数得来。

（2）圆形垂直均布荷载作用下，最大表面沉降发生在圆心处，最小表面沉降发生在荷载圆边界处，且圆心处的表面沉降为荷载圆边界处表面沉降的倍。

（3）正方形垂直均布荷载作用下，正方形荷载中心处的表面沉降为角点处表面沉降的2倍，荷载边界中心处的表面沉降约为角点处表面沉降的1.79倍。

（4）由 Boussinesq弹性理论竖向位移解推导出的圆形刚性承压板形状系数约为 0.818，略大于相关规范提供的 0.785，推导出的方形刚性承压板形状系数约为0.935，略大于相关规范提供的0.886，虽然对计算结果影响不是很大，但从原理上却更为清晰合理一些。

本文系统地解答了有关浅层平板载荷试验中变形模量计算公式的来源问题，对相关学者全面的了解此类问题有一定指导和借鉴意义。