格点问题解法探析

龚 杰

(江苏省南通市海门区海南中学 226100)

格点问题是数学创新题的重要题型之一，如何熟练掌握并灵活解答这类问题，值得我们进行深入探究.以下就格点问题进行探索.

1 作指定边上的高，三等分三角形的面积

例1 如图1是由小正方形组成的6×6网格，△ABC的三个顶点A、B、C都在格点上．用无刻度的直尺，运用所学的知识作图(保留作图痕迹)．

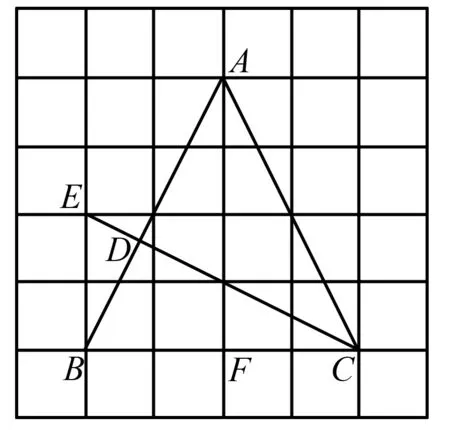
图1

(1)在图1中作△ABC的高CD；

(2)在图2、图3中，分别用两种不同的方法，将△ABC分割成三个面积相等的三角形．

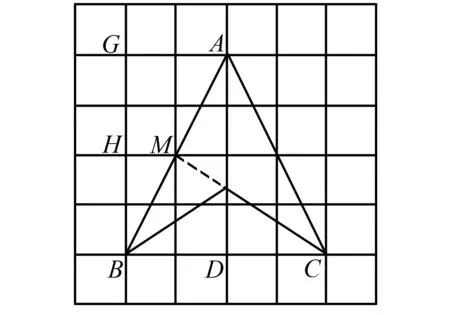
图2

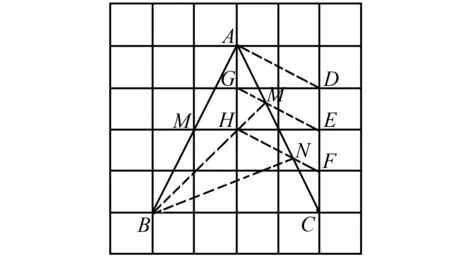
图3

分析(1)如图1,取点E，连接CE，交AB于点D，用SSS证明△EBC≌△BFA，利用互余原理证明.

(2)方法1取BC的中点，构造三角形ABC的一条中线；利用三角形中位线定理，确定AB的中点，确定另外一条中线，中线的交点就是三个三角形的公共顶点，与三角形ABC的顶点构成的三角形就是所求.

方法2如图3，连接AD，则CF=FE=ED=1，利用平行四边形的判定，平行线分线段成比例定理，确定AC的三等分点，利用等底同高的三角形面积相等，实现解题目标．

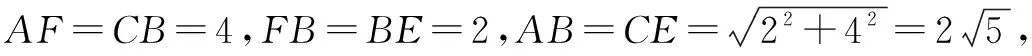
(2)方法1如图2，取BC的中点D，连接AD，则AD是三角形ABC的中线，取BG的中点H，设H所在直线与AB的交点为M，因为HM∥AG，BH=HG，所以HM是△ABG的中位线，于是M是AB的中点，连接CM交AD于点F，则△ABF、△ACF、△BCF即为所求.

方法2如图3，连接AD，则CF=FE=ED=1，连接EG，交AC于点M，因为AG=DE=1，AG∥DE，所以四边形AGED是平行四边形，所以AD∥GE.连接FH，交AC于点N，因为GH=EF=1，GH∥EF，所以四边形EGHF是平行四边形，所以AD∥NF，所以M，N是AC的三等分点，则△ABM，△MBN，△NBC即为所求．

点评画图时，把握好如下几个关键点：准确理解等腰三角形的性质，灵活选择三角形全等，是解题的基础.灵活运用平行四边形的判定和性质，也是画图时重要依据之一，也是画图时需要思考的重要方向；准确把握和运用三角形中位线定理也是画图的重要知识支撑，也是知识综合能力重要体现.

2 作指定底边的等腰三角形

例2如图4，在10×10的正方形网格中，点A，B均在格点上，请按要求画图．

图4

在图中找一点C，使得△ABC是以AB为底的等腰三角形．

分析以最左下端点为原点，以水平格线为x轴建立平面直角坐标系，确定A，B的坐标，设C(x，y)，根据CA=CB，建立方程，化简得到点C的运动直线解析式，根据点C是格点，确定方程的整数解，从而确定等腰三角形的位置．

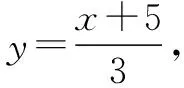
点评画图时，要把握好如下几点：正确理解等腰三角形的判定，这是画图的基础所在；学会把点的位置确定转化为点的坐标来求解，借助方程的整数解实现解题目标，这种数学思维显得很重要.

3 画菱形、正方形

例3如图5，在每个小正方形的边长均为1的方格纸中，有线段AB和线段CD，点A、B、C、D均在小正方形的顶点上．

图5

(1)在方格纸中西出以AB为对角线的正方形AEBF，点E、F在小正方形的顶点上；

(2)在方格纸中面出以CD为一边的菱形CDMN，点M、N在小正方形的顶点上，且菱形面积为8；请直接写出△EFN的面积．

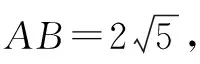
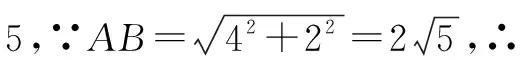
点评通过问题的解决，有如下几点感悟：灵活运用勾股定理，用直尺画图即可；画图也有结论的开放型特点，解答时，需要展开视野，深刻思维，在作图中培养数学发散思维的能力；作图与计算是两种能力的有机交融，作图是动手操作能力，计算是数学最基础最基本的计算能力，作图讲究技能，计算也要讲究技巧，这也提醒大家，常态学习中，要重视和运用每一个知识点，不能因为思维定势，思维习惯，计算习惯，而错失历练发散思维的好机会.

4 解后反思

首先，格点正方形问题题型新颖，在考试中会让学生耳目一新，颇感兴奋；其次，格点图形简单，考查知识明确，解答时需要用如下方法解决：通常把格点正方形的边长看成1，便于计算；格点线段，连接格点所得到的线段；格点线段一定是某个直角三角形的斜边；运用勾股定理一定可求格点线段的长度；运用勾股定理逆定理可以判定格点三角形的形状；把特殊三角形，特殊四边形的性质，判定和性质，往往也是解题的重要思考方向，甚至是解题的首选.