基于k-nearest算法的增强型正交各向异性多孔结构设计
2023-01-12蔡和伦谢卓尊江开勇
曹 伟,蔡和伦,谢卓尊,刘 斌,江开勇
(华侨大学 福建省特种能场制造重点实验室/厦门市数字化视觉测量重点实验室,福建 厦门 361021)
0 引言
多孔结构具有比强度高、比表面积大、轻量节材、馈能减振等优点,被广泛应用于航空航天、汽车工业、生物医疗等众多领域。近年来,随着增材制造技术的飞速发展,使得具有复杂内部多孔结构的零件制造成为可能,因此多孔结构的轻量化、定制化设计和建模逐渐成为当前增材制造技术最具挑战性的研究方向之一,主要表现为建模过程复杂、数据量庞大、计算和仿真成本较高等。此外,对于更加复杂的功能梯度多孔结构(Functionally Gradient Porous Materials, FGPMs),要求根据零件局部应力大小和方向设计其内部结构,在保证几何连续的情况下满足梯度力学性能,极大地增加了设计复杂度。
根据建模方法的不同,多孔结构可以分为规则多孔结构和不规则的随机多孔结构。由于设计方便、可控性高,早期的多孔结构大多基于规则胞元的晶格结构,即采用规则胞元阵列填充设计空间,主要包括蜂窝结构、菱形晶格结构、立方体结构、三周期极小曲面等[1-3]。蜂窝结构是一种由众多柱状孔穴胞元密铺组成的多孔结构,这种结构在节省材料的同时,保证了较高的比强度与比刚度。邢昊等[4]针对二维蜂窝结构在共面方向集中载荷作用下承载性能不足的问题,提出一种基于拓扑优化密度映射的非均匀蜂窝结构建模方法。针对多孔结构内部支撑难以去除的问题,WU等[5]提出一种自支撑的菱形晶格结构,并用该结构填充零件内部,通过调节不同晶格的壁厚实现力学性能的梯度分布;WANG等[6]提出一种改进的面心立方多孔结构设计方法,通过选择性激光融化(Selective Laser Melting, SLM)工艺打印后研究其抗冲击行为。三周期极小曲面(Triply-Periodic Minimal Surface, TPMS)是一种数学上定义的空间结构,整个结构没有自交点,具有无限延伸表面和复杂的开孔结构[7]。REN等[8]提出一种多尺度混合TPMS优化设计模型,该模型能较好地解决不同尺度下TPMS间边界的连续性问题,并建立了应力与TPMS之间的映射关系。此外,在上述结构的基础之上,还衍生出一些变异的晶格结构,例如对称双金字塔型的十二面体结构、星型结构等,通过改变连接杆的直径或面的厚度实现力学性能的梯度分布[9-10]。虽然规则晶格多孔结构能够降低设计复杂度、减少设计周期,但是由于其固有特性,其设计自由度较低,对复杂模型的适应性较差,难以进行各向异性设计,可能造成几何结构、力学性能的不连续,限制了其使用范围。
随机多孔结构是一种不规则多孔结构,它不仅适用复杂模型,设计自由度高,还能完美解决规则多孔结构几何、力学性能不连续等问题。典型的随机多孔结构包括基于拓扑优化的多孔结构、基于维诺图的多孔结构等。拓扑优化是一种根据给定约束,在设计域内对材料分布进行优化的方法[11]。DAYNES等[12]提出一种基于拓扑优化的功能梯度多孔结构建模方法,并通过实验证明其强度和刚度远高于同等质量的规则立方体晶格结构。然而,拓扑优化方法大多用于优化二维结构,对三维模型的适用性较差,无法满足对复杂三维结构建模的需求。维诺多孔结构是一种模拟自然界物体的理想结构,如骨骼、海绵等。MARTNEZ等[13]提出一种基于直杆的三维维诺多孔结构的高效设计方法。在此基础上,LIU等[14-15]将三维维诺图与隐式曲面相结合,设计了一种全连通的光滑多孔结构,有效避免了应力集中。虽然三维维诺多孔结构可控性强、结构连续,但建模复杂度高,且难以实现各向异性多孔结构的建模。
1 增强型正交各向异性多孔结构建模
1.1 建模流程
本文提出的基于改进k-nearest算法的增强型正交各向异性多孔结构的设计流程如图1所示,其初始输入条件包括站点密度场ρ和方向场φ。首先,采用站点随机采样算法将密度场映射为设计域内的站点分布,控制正交各向异性多孔结构力学性能的梯度分布;在设计域内叠加方向场,将其映射为黎曼空间中的流形场,实现多孔结构局部正交各向异性的任意旋转。需要说明的是,初始的密度场ρ和方向场φ可以从模型有限元分析的应力场提取,也可以交互式输入。其次,计算邻域内站点间的黎曼距离,采用改进的k-nearest算法连接相邻的k(k≥2)个站点,生成2D多孔结构模型;最后,对生成的2D多孔结构在厚度方向进行拉伸,可以得到2.5D多孔结构模型,并最终通过3D打印机打印成型。

1.2 站点随机采样
站点的随机采样是建立多孔结构的基础,本文提出一种密度场驱动的站点随机采样算法,先将设计域离散化为一系列正方形栅格,然后通过给定的密度场函数ρ在每一个网格中进行随机采样。以二维设计域为例,站点随机采样过程如图2所示,具体算法如下:
步骤1将二维设计域离散为边长为a的正方形栅格。
步骤2根据站点密度函数场ρ,计算栅格i内的站点数量ti=a2ρi。
步骤3将栅格i等分为4个正方形子栅格。
步骤4若栅格i内的站点数量ti≤4,则随机选取ti个子栅格,并分别在每个子栅格内部任意位置随机生成一个站点。
步骤5若ti>4,则转步骤2,重新计算子栅格中的站点数,划分栅格,并随机生成站点(如图2)。重复步骤2~步骤5,直至所有区域的站点分配完成。
对于3D模型,其站点随机采样算法和上述2D模型的算法类似,不同之处在于:需要将3D模型对应的三维设计域离散化为边长为a的立方体栅格,然后将每个栅格平均划分为8个边张相等的子栅格,一般采用八叉树结构表示。

从图2可以看出,设计域内站点的分布是由密度场ρ驱动的,是多孔结构实现弹性性能梯度分布的根本因素,其原因在于站点分布的特征决定了材料局部分布,从而直接影响其局部力学性能。即站点分布密集的区域,材料分配相对较多,力学性能相对较高;相反地,站点分布稀疏的区域,材料分配较少,力学性能相对较低。因此,该算法可以通过站点密度分布函数从宏观上控制多孔结构不同部位的力学性能,在应力较大的部位设置较大的站点密度,增加力学性能;反之,在应力较小的部位设置较小的站点密度,节约材料。此外,在微观上又能保持局部随机性,从而保证梯度多孔结构的几何连续性。
随机采样算法中输入的密度场函数ρ可以由用户指定,也可以从模型的有限元分析得到,如图3所示。
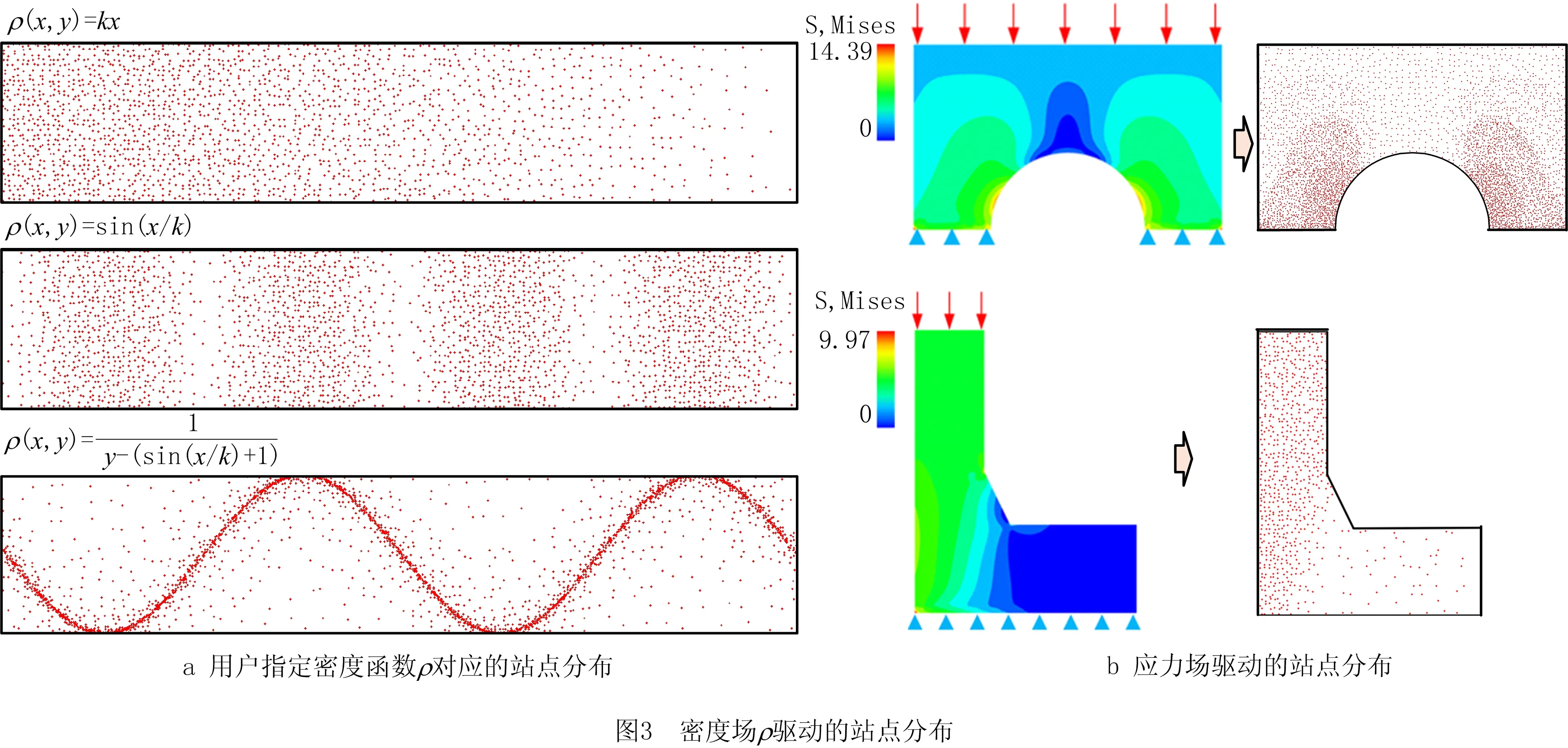
1.3 方向场
方向场主要用于控制正交各向异性多孔结构正交轴的旋转方向。对于设计域中任意点邻域内的多孔结构单元,其强度最高的正交轴方向始终与方向场保持一致,从而增强多孔结构的力学性能,降低材料消耗。方向场可以有多种形式,如场函数、流形场、应力方向场等。
1.4 改进的k-nearest算法
将方向场映射为黎曼空间中的流形场,采用黎曼距离计算站点间的“距离”,实现任意局部区域各向异性方向的旋转,从而建立起具有梯度弹性性能的多孔结构。为方便理解,本节以二维黎曼空间为例阐述各向异性多孔结构的建模过程,且可以较为容易地拓展到三维黎曼空间。
1.4.1 黎曼度量
设点p是二维黎曼空间Ω中的一点,p点处的度规张量矩阵M(p)可视为一个正定矩阵,即
(1)
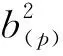
M(p)=ETUE,
(2)

(3)
(4)
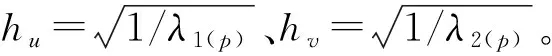
定义1设坐标点p与q是黎曼空间Ω中任意两点,M为p点对应的黎曼度量,则从p点到q点的有向距离dp(p,q)定义为:
(5)
由于M(p)≠M(q),在黎曼空间中点p与点q的距离是非对称的,会导致p到q的有向距离与q到p的有向距离在数值上不一致,即dp(p,q)≠dq(q,p),因此本文将两点间的“距离”定义为:
(6)
1.4.2k-nearest算法
如图5所示为采用文献[16]中的k-nearest算法设计的正交各向异性多孔结构:依次遍历所有站点,对每个站点采用直线连接与其“距离”最近的k(k=2,3,4,…)个站点,并赋予每条直线宽度t(即2.5D多孔结构的壁厚,t≥2τ,τ为打印机的最小打印尺寸,如打印机喷头直径等)和厚度h,即可生成最终的2.5D正交各向异性多孔结构。

1.4.3 算法改进
从图5可以看出,采用k-nearest算法生成的各向异性多孔结构存在两个明显缺陷:
(1)在站点分布相对稀疏的区域会沿方向场生成较大的孔洞,这种孔洞比期望的孔洞大一个量级,如图5b中橙色圈所示。
(2)在站点分布相对密集的区域,多条线段会产生交叉现象。交叉点相当于增加了站点数量,导致实际站点密度和期望的站点密度ρi存在较大误差,如图5b中蓝色圈中所示。
这种不均匀的孔洞分布以及新增的站点,不仅使多孔结构不符合设计要求,还会导致材料分布不均匀,产生应力集中,严重影响多孔结构的整体力学性能。此外,在后续模型3D打印成型时受限于打印机的精度,过于细小的孔洞(r≤2τ)几乎无法打印。经过分析发现,产生上述两种缺陷的根本原因是由于算法没有考虑站点连线相交的情况。
基于此,本文提出一种改进的k-nearest算法,可以判断并去除会产生相交的线段,确保每个站点均连接k个相对“最近”的站点。具体算法如下:
步骤1在欧式空间中,计算当前站点ni的邻域,将邻域内的站点存入存储器Neighbour中。对2D/3D设计域,站点ni的邻域半径rni分别为:
(7)
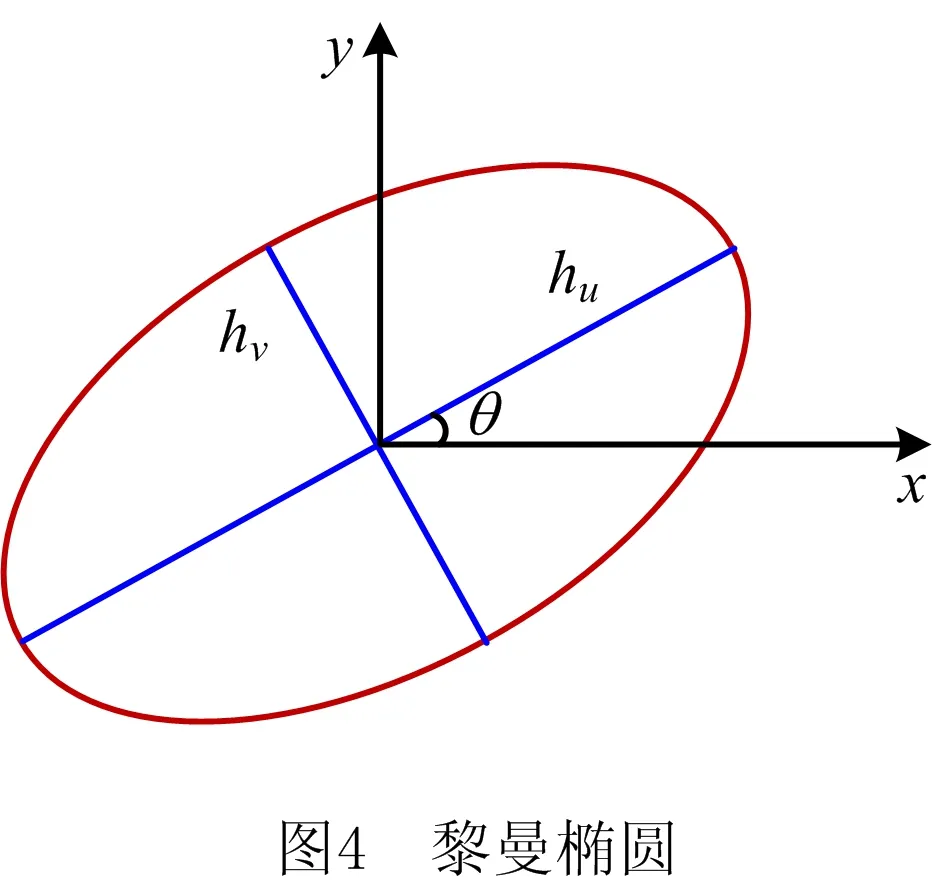
(8)
其中:a为设计域内划分栅格的边长;hui、hvi和hwi分别为ni对应的黎曼椭圆/椭球各轴的长度。该方法保证邻域内存在满足条件的k个站点的同时,又避免了在黎曼空间中进行全局搜索,提高了算法效率。
步骤2在黎曼空间中,按式(6)计算ni与邻域(Neighbour)内站点的“距离”,并从小到大排序。
步骤3依次从排序后的Neighbour取出站点,判断ni与该点的连线与已生成的结构M是否相交。若不相交,则用线段连接两站点,并更新M;若相交,则放弃连接。重复步骤3,直至与ni连接的站点数等于k为止。
步骤4遍历设计域内所有站点,重复步骤1~步骤3。
图6中上下两栏分别为采用文献[16]中的k-nearest算法和本文算法在站点分布相同、不同的各向异性度量hx∶hy(x和y为正交轴)下生成的2.5D多孔结构。不难发现,本文算法能够明显地减少上述两种缺陷,使材料分布更均匀,从而增强了多孔结构的力学性能。

本文算法也能比较容易地拓展至三维空间,区别在于需要用直径为d的圆柱体支杆代替二维空间中的线段,判断当前生成的支杆是否会与已生成的结构M产生干涉,并采用布尔运算对新支杆与M的三角网格进行求交。算法伪代码如表1所示,生成的三维多孔结构如图7所示。可以看出,通过调整hu、hv和hw的比例,可以非常方便地控制多孔结构在不同正交轴向的各向异性程度。

表1 三维正交各向异性多孔结构生成算法

1.4.4k值的选取
本文算法的核心是将站点p与其相对“最近”的k个站点相连,因此,k值的选取十分关键,对多孔结构的连通性和力学性能都有较大的影响。图8所示为不同k值对应的二维结构,可以发现:当k=2,3时,几何连通性很差,无法生成多孔结构;当k=4,5时,虽然能够生成多孔结构,但是仍存在局部区域不连通,影响了多孔结构结构的力学性能;当k≥7时,虽然结构几何连通性较好,但过于紧凑,降低了多孔结构的设计空间。而BALISTER等[17]已经证明当k=6时候,生成的结构最优,即具有相对较好的几何连通性和较大的设计空间。因此,在默认情况下本文后续章节中所建立的多孔结构其k值均为6。

2 多孔结构的性能分析
2.1 各向异性多孔结构的数值均质化
数值均质化是面向周期性或近周期性材料宏观性能的有限元分析方法,广泛应用于复合材料研究。由于本文算法中的站点生成器是均匀分布的随机序列,所生成的站点具有随机性,从概率意义上,当站点密集时,即模型宏观尺寸相对于平均孔径足够大时,模型整体结构呈现近周期性。因此,数值均质化方法仍然适用于本文多孔结构的分析[15-16]。这种达到近周期性体积的多孔结构模型被称作代表性体积单元(Representative Volume Element, RVE),是数值均质化的分析对象。
数值均质化能有效地确定周期性复合材料的弹性张量。设材料单元为V,体积为|V|,在材料弹性变形阶段,应力σ与应变ε成线性关系[18]:
σ=Cε。
(9)
其中C是弹性矩阵,用于表征材料的弹性行为。
为方便编程实现,本文采用ANDREASSEN等[19]提出的方法,将多孔结构模型划分为正方形网格,对网格单元节点编号,并施加周期性边界条件,通过线弹性方程kχ=f求解出χij,可得到均质化弹性张量为:
(10)
其中:i、j为对应矩阵的第i、j行/列;k为刚度矩阵;f和χ分别是等效节点的载荷列阵与位移列阵;ke为单元刚度矩阵;χe表示对应网格单元节点的整体位移列阵,可以从χ的对应节点中提取;Ve表示对应网格单元的体积;N为RVE单元划分的有限网格单元总数量。需要说明的是,上式仅适用于描述多孔结构材料的弹性变形行为,而无法描述材料达到屈服极限后的塑性变形或断裂行为。
2.2 弹性性能分析
2.2.1 数值均质化分析
为分析本文正交各向异性多孔结构的弹性性能,对图6中k-nearest算法和本文算法生成的4组2.5D多孔结构进行数值均质化分析。所有结构的尺寸均为50×50×7 mm3,壁厚t=0.4 mm。每组模型的站点分布相同,且站点是均匀随机分布的。4组多孔结构的各向异性度量hx∶hy分别为1∶1、1∶3、1∶5和1:7,其中x、y为正交轴。从图中可以看出,当hx∶hy=1∶1时,所生成的多孔结构呈各向同性;当hx∶hy≠1时,对应的多孔结构呈明显的正交各向异性,且比例越大(或越小),各向异性程度越高。
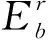
(11)
(12)
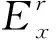

表2 不同多孔结构的弹性性能分析与对比
由表2可以看出,本文算法生成的多孔结构的相对密度比k-nearest算法生成的有所增加,其增量分别为16.2%、14.3%、17.5%,平均增加16.0%。主要原因是k-nearest算法连接的是绝对“最近”的k个站点,而本文算法为避免产生相交,连接的是相对“近”的站点,因此杆的平均长度要长于k-nearest算法,导致相对密度增大。虽然本文算法生成的多孔结构相对密度较大,但是其弹性性能相对于k-nearest算法大幅增强,以hx∶hy=1∶3为例,本文算法生成的多孔结构在x、y方向上的相对弹性模量分别增强了133.3%和26.9%。
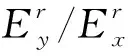
2.2.2 压缩实验
为进一步研究上述正交各向异性多孔结构的力学性能,验证数值均质化结果的准确性,将图6中的4组多孔结构采用熔融沉积成型(Fused Deposition Modeling, FDM)工艺进行3D打印成型,打印材料选择为聚乳酸(Polylactic Acid, PLA),基体弹性模量为1 200 MPa。每种多孔结构打印2组,分别沿x、y方向进行压缩实验。实验设备为万测电子万能试验机(型号:TSE504D),速率设置为1 mm/min,实验结果如图9所示。

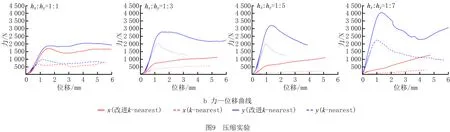
从图9b中各组试样的力—位移曲线可以看出,在多孔结构发生塑性变形之前,本文算法生成的多孔结构能够承受更大的载荷;随着多孔结构各向异性程度增加,y方向能承受的最大载荷值逐渐增大,同时x方向能承受的最大载荷值逐渐降低,该结果和上一节数值均质化的结果保持一致。
此外,通过压缩实验,还可以测得试样的弹性模量。表3所示为压缩实验测得的试样弹性模量与数值均质化计算的相对弹性模量之间的对比情况。可以看出,对不同拉伸比例下的2.5D各向异性多孔结构,数值均值化方法相对于压缩实验结果的误差较小,最大相对误差仅为9.38%,表明数值均质化方法能较为准确的预测本文提出的各向异性多孔结构的弹性性能。
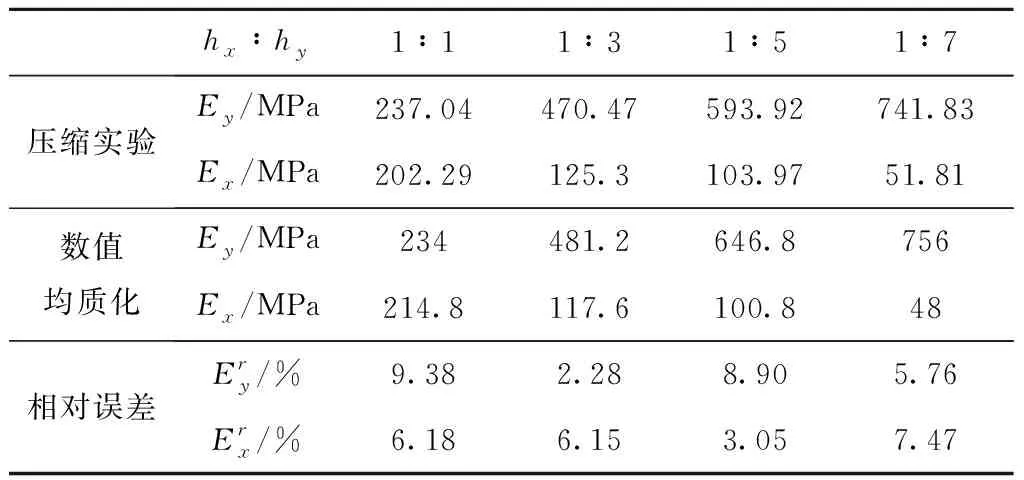
表3 压缩试验与均质化结果对比
对于三维各向异性多孔结构,采用光固化(Stereolithography,SLA)工艺打印了3组试样,材料为光敏树脂,试样在沿三个正交轴方向的拉伸比例分别为1∶1∶1、1∶3∶3和1∶1∶3,尺寸均为40×40×40 mm3,杆直径为d=0.4 mm。对3组试样分别沿着x、y、z方向进行压缩实验,实验结果如图10和表4所示。


表4 三维各向异性多孔结构压缩实验结果 MPa
实验结果表明,随着y、z方向各向异性程度的增加,对应方向的弹性性能也相应提升,而其他方向上的弹性性能逐渐降低。同时,从1∶3∶3和1∶1∶3样品的实验结果还可以看出,仅对一个方向进行拉伸的多孔结构的弹性性能远高于在两个方向同时拉伸的多孔结构。
2.2.3 失效分析
通过上述压缩实验,测得不同多孔结构在y方向的抗压强度如表5所示。可以看出,随着y方向拉伸比例的增加,两种算法生成的多孔结构在y方向的抗压强度逐渐增大,但是本文算法生成多孔结构的抗压强度相比于k-nearest算法有明显的增强,增强幅度均达到200%以上。

表5 各向异性多孔结构的抗压强度
在压缩实验中,当试样承受的压应力超过抗压强度后,试样会发生局部屈服或破裂,进而发生失效,如表6所示(压缩12%)。可以看出,在应变较大时,hx∶hy=1∶1的各向同性多孔结构未表现出明显的失效,且本文结构要优于k-nearest算法生成的结构;而1∶3、1∶5和1∶7的各向异性多孔结构均会发生不同程度的失效,如杆状结构发生较大弯曲变形甚至断裂,且失效大多发生在孔洞较大的位置,与1.4.3小节的分析一致。其原因主要是k-nearest算法会导致材料分布不均匀,在孔洞较大的位置材料分布较少,从而产生应力集中。虽然本文设计的增强型多孔结构能在一定程度上使材料分布更均匀,提高了力学性能,但是并不能从根本上解决这一问题,当多孔结构各向异性程度增大时,材料分布的不均匀性也随之增大。

表6 各向异性多孔结构的失效分析(压缩12%)
2.2.4 随机性分析
由于站点是在密度场驱动下随机采样的,这种随机性可能会对多孔结构的弹性性能产生影响,造成性能的不稳定。为研究随机性的影响程度,在保持站点密度ρ不变的情况下,对hx∶hy=1∶1、1∶3、1∶5和1∶7四种拉伸比例各随机生成了3组多孔结构,尺寸为50×50×7 mm3,壁厚t=0.4 mm,如表7所示。从模型外观上看,站点分布的随机性对多孔结构的影响不大。

表7 随机生成的站点与对应的多孔结构

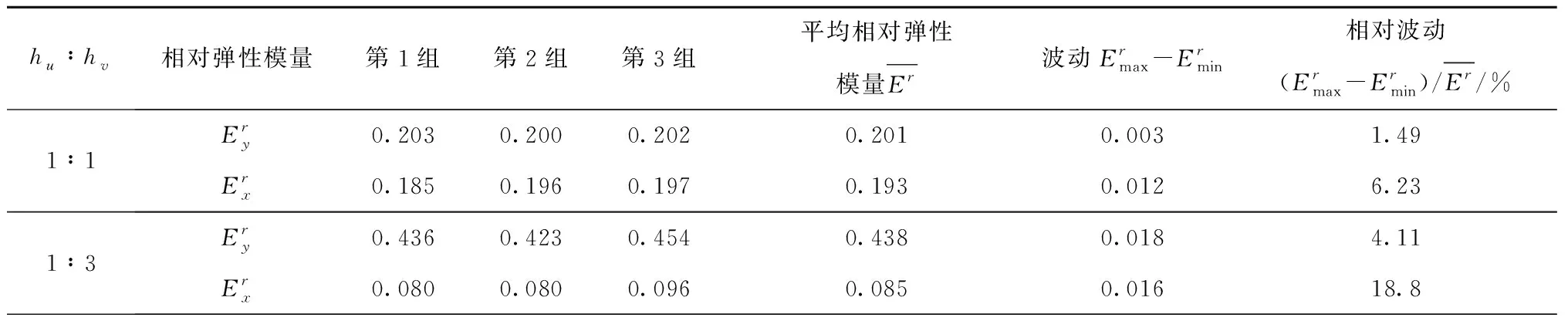
表8 站点随机性对多孔结构弹性性能的影响

续表8
2.2.5 弹性设计空间
为了研究本文提出的各向异性多孔结构的弹性设计空间,本文随机生成了大量相同尺寸的2.5D多孔结构(约2 400个),其拉伸比例hx∶hy范围选取为10∶1到1∶10,旋转角度θ=0。对这些多孔结构逐一进行数值均质化分析,将其结果绘制成散点图如图11所示。可以看出,各向异性多孔结构对应的点均匀分布在对角线的两侧,且呈对称分布,即hx∶hy>1对应的多孔结构分布在对角线的下方,而hx∶hy<1对应的多孔结构分布在对角线上方。同时,随着拉伸比例的增大,各向异性程度增大,对应点距离对角线越远。当hx=hy时,多孔结构呈各向同性,对应点分布在对角线上。

图11中散点覆盖的区域即为本文所提出的多孔结构(2.5D)的弹性设计空间,在多孔结构壁厚为常量时,其弹性性能主要受两个设计参数的影响,即拉伸比例hx∶hy和站点密度ρ。其中,hx∶hy与多孔结构的各向异性呈正相关,ρ与多孔结构的宏观弹性性能呈正相关。需要说明的是,图11所示的多孔结构设计空间仅适用于线弹性阶段,多孔结构发生塑性变形时的力学性能并不在本文的讨论范围之内。
2.3 案例
本节主要讨论正交各向异性多孔结构的应用情况,建模过程均采用Visual Studio 2013的MFC框架,搭配CUDA程序并行计算,在硬件环境为Inter Core2 i5-10400 CPU,16 GB内存与NVIDIA GeForce GTX 1650显卡的计算机上实现,最后通过3D打印机打印成型。
2.3.1 应力驱动的梯度多孔结构
如图12所示为采用本文方法设计应力驱动的梯度各向异性多孔梁结构的建模过程。首先对梁结构进行有限元分析,得到如图12a所示的应力场。将应力大小映射为站点密度场,通过1.2节的随机采样算法可以生成如图12b所示的站点分布;同时,将应力方向映射为如图12c所示的方向场。最后采用1.4节提出的改进k-nearest算法生成如图12d所示的2.5D正交各向异性多孔结构。梁模型的尺寸为250×50×30 mm3,壁厚t=1 mm,体积分数为43%。为对比分析,本文还设计了如图12e所示的蜂窝结构,其尺寸、壁厚均与图12d中的多孔结构相同。此外,通过调整蜂窝结构的胞元大小,使其体积分数也为43%。

采用SLA3D打印机将上述两种结构打印成型,打印材料为光敏树脂。分别对其做三点弯曲破坏性实验,如图13a所示,实验设备为万测电子万能试验机(型号:TSE504D),选用弯曲夹具,速率设置为1 mm/min。实验测得的力—位移曲线如图13b所示,其他测试结果如表9所示。
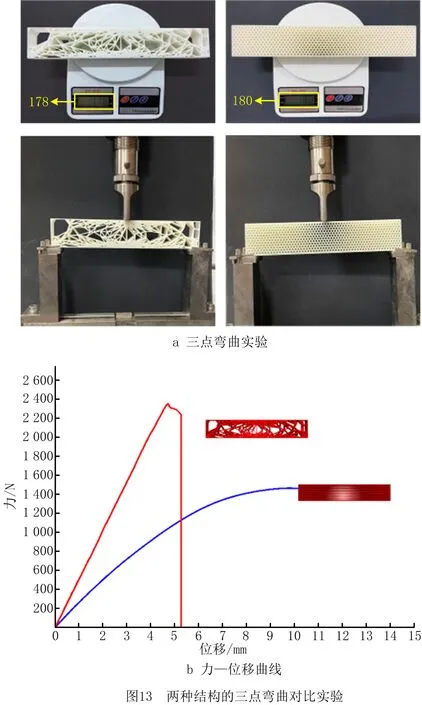
表9 两种结构的三点弯曲实验结果比较

项目重量/g最大载荷/kN弯曲模量/MPa弯曲强度/MPa蜂窝结构1801.46828 258.1880.1各向异性多孔结构1782.35366 454.81 413.3提升率/%-1.1160.29135.1760.58
不难看出,在两种结构的重量在几乎相等的条件下,相比于规则的蜂窝结构,本文方法设计的应力驱动的梯度多孔结构的力学性能大幅提升,最大载荷、弯曲模量和弯曲强度分别提升了60.29%、135.17%和60.58%。这是由于本文方法能够通过站点密度分布调整局部材料的分布,在应力较大的部位分配较多材料,应力较少的部位减少材料分配,实现在相同材料用量的情况下,提升多孔结构力学性能;或在承受相同载荷的情况下,降低材料的用量,达到绿色节材的目的。
需要说明的是,由于图12b中的站点分布是由设计者根据应力场和设计经验综合设置的密度场函数随机采样得到的,由站点分布驱动的梯度正交各向异性多孔结构只是一个较优的结构,还存在一定的优化空间。若要获得最优的多孔结构,使材料分布更符合应力分布,则需要通过实验、仿真或机器学习等方法建立应力场和站点密度场之间定量的映射模型,从应力场得到最优站点分布,叠加方向场后生成最优的正交各向异性多孔结构,这也是后续工作需要进一步研究的内容。此外,由于站点是随机采样得到的,对外观对称的模型无法实现内部多孔结构的对称(如图12d内部多孔结构左右不对称),从而会在一定程度影响其美学特性。
表10列出了k-nearest算法和本文算法在2.5D机械零件轻量化设计应用情况的对比分析。通过对零件受力情况进行有限元分析,可以得到零件的应力分布。将应力大小映射为设计域内的站点分布,应力方向映射为方向场,分别采用k-nearest算法和本文算法生成了两组多孔结构。可以看出,两种算法生成的多孔结构均能在满足材料屈服极限的条件下实现零件的轻量化,但本文算法生成的多孔结构的最大Mises应力明显小于k-nearest算法,说明本文算法改善了k-nearest算法材料分布不均匀、易产生应力集中的现象,增强了多孔结构的力学性能。此外,若后续工作中能建立应力场和站点密度之间的映射模型,则可以进一步对多孔结构进行优化,实现零件最佳轻量化的目标。
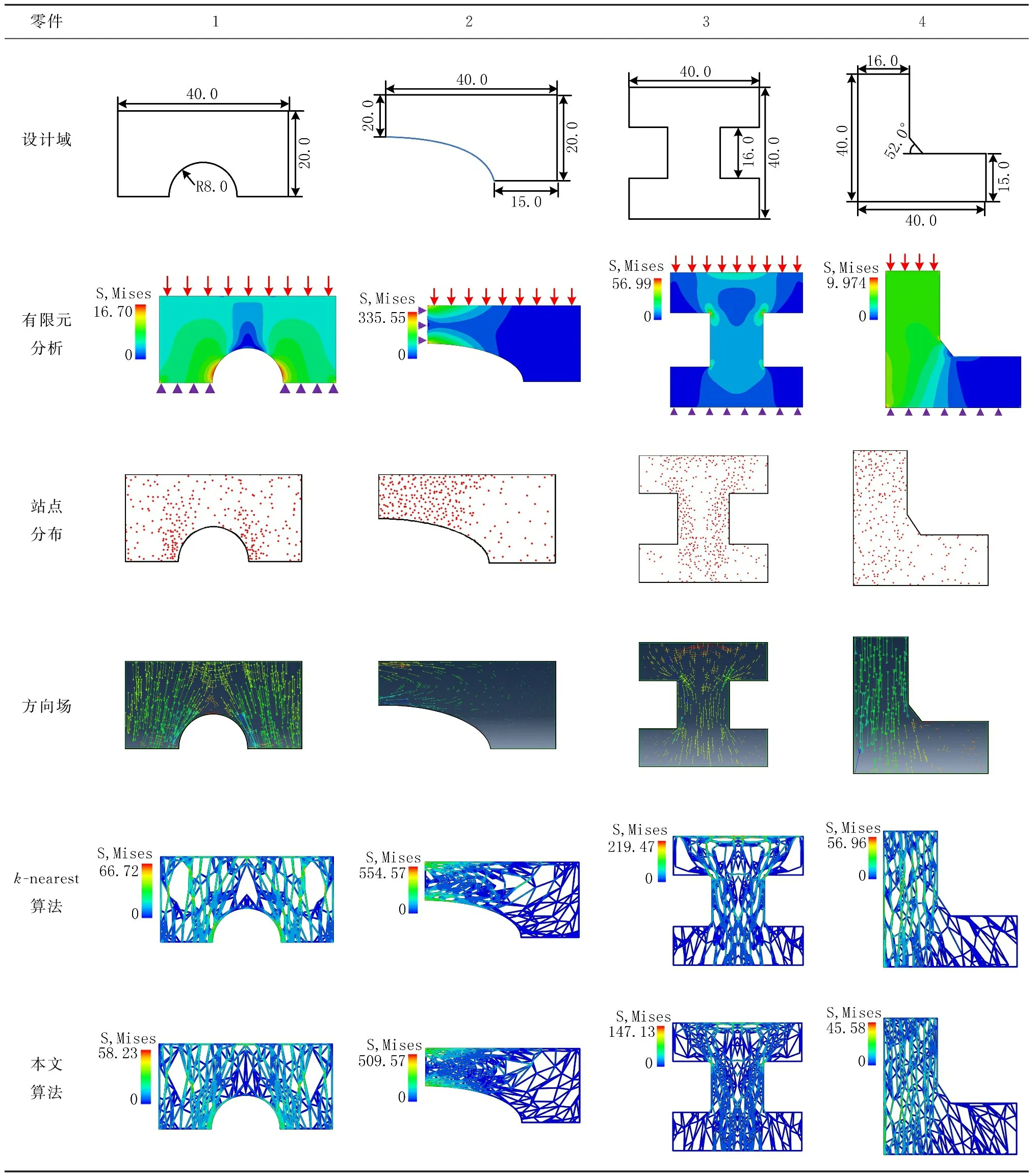
表10 本文算法在机械零件轻量化设计的应用情况
2.3.2 其他应用
本文正交各向异性多孔结构的设计方法还可以应用于其他场景,如图14所示。图中模型均采用FDM工艺打印,材料为PLA。其中,图14a为2.5D椅子模型,通过设置方向场,可以实现座位、靠背和椅腿等部位的正交各向异性。图14b为3D牙齿模型,其内部被3D正交各向异性多孔结构填充。根据牙齿的受力情况,可以发现多孔结构沿竖直方向和径向呈正交各向异性,在实现牙齿模型轻量化的同时,又能保证在上述两个方向上的强度。图14c为采用正交各向异性多孔结构填充的3D车轮模型,多孔结构在轮毂部分沿径向拉伸,使轮毂能够承受较强的径向力;在轮胎部分沿周向拉伸,使轮胎相对柔软,从而在运动时实现缓震的功能。

3 结束语
本文提出一种基于k-nearest算法的增强型正交各向异性多孔结构设计方法,通过站点密度场驱动站点的随机采样,通过改进k-nearest算法,叠加全域方向场,生成增强型正交各向异性多孔结构,并通过3D打印机将多孔结构打印成型。最后,分别通过数值均质化和压缩实验对打印的多孔结构进行力学性能、失效状态和随机性进行了分析和讨论。实验结果表明,采用本文方法设计的正交各向异性多孔结构具有更优良的弹性性能和更大的弹性设计空间。此外,本文提出的正交各向异性多孔结构设计方法可控性高,不仅可以通过黎曼椭圆/球的拉伸比例控制局部正交各向异性程度,通过方向场控制各向异性的朝向,还可以通过站点密度场调控多孔结构力学性能的梯度分布。
虽然多孔结构性能明显增强,但本文方法在实际工程应用中仍存在一定的局限性,即并不能从根本上解决局部材料分布不均匀的情况,尤其是各向异性较大的区域。其次,由于本文未建立起应力分布与站点密度函数之间的数学映射关系,导致在设计时需要根据设计师经验生成站点的随机分布,无法实现设计过程的智能化和结果的最优化。后续工作包括:1)解决局部材料分布不均匀问题;2)建立应力场与多孔结构设计参数之间的数学模型,将应力大小映射为站点密度,将应力方向映射为多孔结构的方向场,从而建立应力驱动的梯度多孔结构模型。
