基于区间二元语义距离测度的多属性群决策方法
2023-01-11陈晶,姚陈
陈 晶,姚 陈
(1.湖南高速铁路职业技术学院,421001,湖南,衡阳;2.南华大学化学化工学院,421001,湖南,衡阳)
0 引言
由于多属性决策问题具有复杂性、不确定性以及人们思维具有模糊性,决策方案的属性值通常难以用准确的数字来度量,用定性的语言术语却能满足评价的需要[1-14]。如对人的品行测评时,通常适用“好”“一般”和“差”等语言术语评价。自1998年Delgado等[1]首次提出用语言术语表达评价信息以来,语言型决策理论与方法引起国内外学者的广泛关注。Herrera等[2]为避免离散的语言术语在运算时出现信息失真,提出了集成语言评价信息的二元语义分析法。王欣荣和樊治平[3]把二元语义引入语言型决策问题中,提出基于二元语义评价模型的逼近理想解法。卫贵武[4]推广诱导有序加权几何(IOWG)算子[5]到二元语义环境中,提出二元语义诱导有序加权几何(T-IOWG)算子,并给出一种基于T-OWG和T-IOWG算子的多属性群决策方法。王晓等[6]针对属性值为区间二元语义且属性权重信息完全未知的情形,提出一种基于离差最大化的属性权重客观赋权方法。刘勇等[7]通过设计多时段的逼近理想解法,构造出以灰色关联度偏差最小化为目标的区间二元语义群决策模型。Li等[8]拓展诱导广义有序加权平均距离(IGOWAD)算子[9],提出二元语义诱导有序加权平均距离(2LIOWAD)算子、诱导广义有序加权平均距离(2LIGOWAD)算子,并对算子的性质进行了分析。张娜等[10]给出等信息量转换区间二元语义的“核”运算和“半径”运算,并基于区间二元语义距离测度构建多属性群决策模型。王中兴等[11]扩展Archimedean S模,定义对属性权重自适应调整的二元语义扩展Archimedean S模集成(TASTA)算子、加权平均(TASTWA)算子和向量加权平均(V-TASTWA)算子,并将其应用于权重值未知的多属性决策中。Liang等[12]基于多粒度区间二元语义广义距离测度,给出一种处理区间二元语义信息的交互式多准则(TODIM)群决策方法。Feng等[13]针对属性信息相互关联的群决策问题,提出二元语义关联加权Maclaurin对称均值(2TLDWMSM)算子、关联加权广义Maclaurin对称均值(2TLDWGMSM)算子等。Song和Li等[14]给出求解决策方案优先权重的目标规划模型与群体一致度的自动迭代算法,并将其应用于多粒度二元语义群决策问题。
上述语言型决策方法基本上是借由语言术语运算去集成语言评价信息提出的,而目前语言术语的运算存在着诸如集成结果违反人们直觉或越界的不足[11]。因此,有关语言术语的运算或集成方法的研究显得很有必要。Lan等[15]为避免决策中的语言评价信息出现运算越界情形,引用效用理论到决策环境中,提出一种基于效用距离测度的不确定语言集成(ULAf)算子。王中兴等[16]结合Archimedean S模与T模,给出不确定语言变量的一种加权组合集成算法,该算法能有效克服语言型运算违反人们直觉和越界的不足,但对于准则隶属度值为“1”且非隶属度值为“0”的情形该算法则无法处理。
为克服决策中的语言评价信息存在着上述问题,本文基于区间二元语义欧式距离测度,给出各个体区间二元语义与集成结果间的偏差,通过偏差最小化模型得到群体语言评价信息的集成新方法,以及通过定义备选方案间的相对偏差和备选方案关于正、负理想解的相对贴近度,给出各方案的一种优劣排序法。最后,将所提方法应用于不确定语言环境中,为语言型决策提供新思路新方法。
1 预备知识
1.1 语言术语集
语言术语集S={s1,s2,…,sτ}是非空离散集合,si是预先定义的语言术语(如“差”“一般”“好”等)。正整数τ表示语言术语集的粒度。例如,七粒度语言术语集可表述为S={s1,s2,s3,s4,s5,s6,s7}={极差,差,较差,一般,较好,好,极好}。语言术语集S通常有如下定义[1]。

3)否定算子:neg(si)=sτ+1-i。
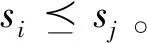
1.2 二元语义与区间二元语义
二元语义是指通过二元组(si,αi)的形式来分析语言评价信息,其中si∈S为语言术语;αi∈[-0.5,0.5)为符号转移值,表示集成结果与S集中最贴近的语言术语si的偏差。
定义1[2]:设si∈S为语言术语,则si可由函数ϑ:S→S×[-0.5,0.5)转化为二元语义,即ϑ(si)=(si,0)。
定义2[2]:设β∈[1,τ]为语言术语经集成后所对应的实数,则β可由函数Δ:[1,τ]→S×[-0.5, 0.5)转化为相应的二元语义,即Δ(β)=(si,αi)。其中i=round(β),αi=β-i∈[-0.5,0.5),“round”为四舍五入取整函数。相应的,二元语义(si,αi)可由Δ的逆函数Δ-1:S×[-0.5,0.5)→[1,τ]转化为对应实数β∈[1,τ],即Δ-1(si,αi)=i+αi=β。
定义3[2]:对于二元语义(si,αi),(sj,αj)∈S×[-0.5,0.5),其序关系为
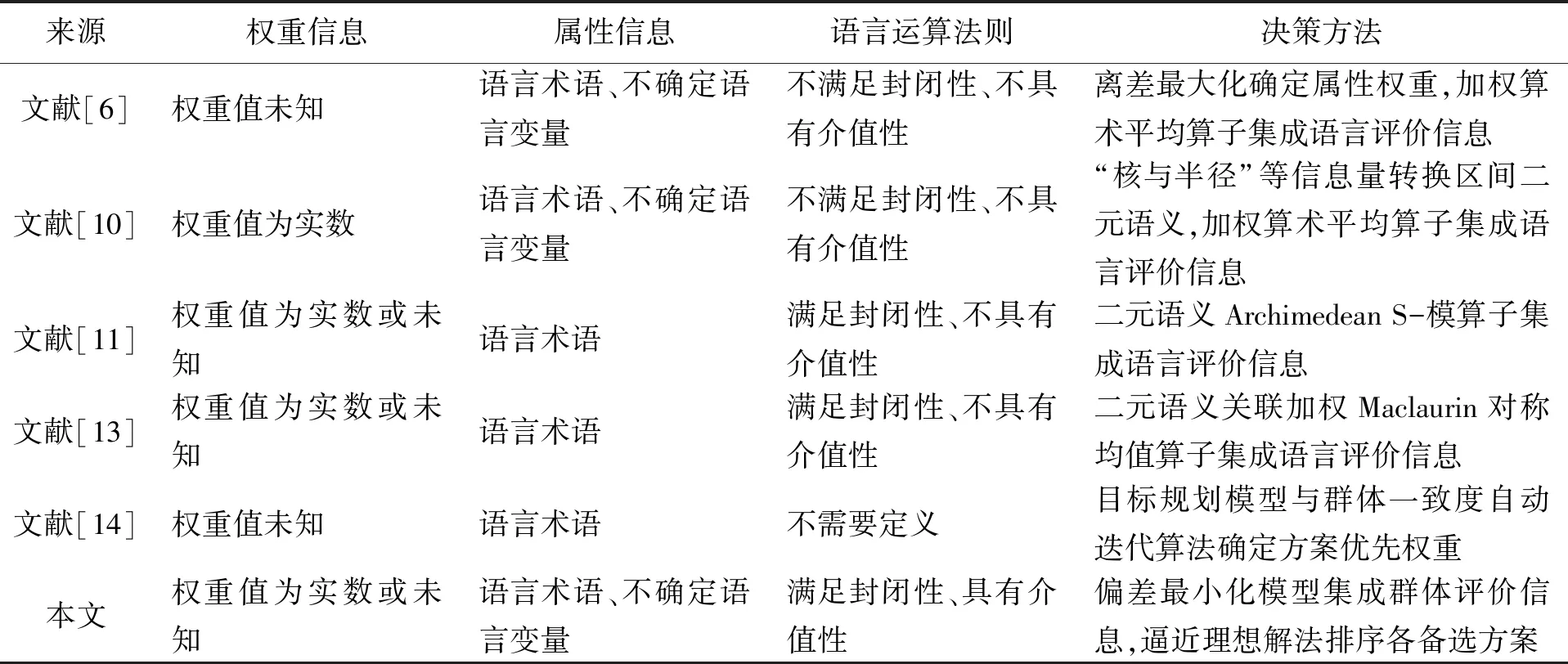
1)若i 2)若i=j,则:①当αi<αj时,则(si,αi)(sj,αj);②当αi=αj时,则(si,αi)=(sj,αj)。 (1) 在实际的决策问题中,各决策专家针对评价对象所给出的评价往往存在着差异。将多个专家不同的评价信息进行集成,得到的群体评价是群体专家意见的综合反映,因此群体评价与各专家评价之间的偏差应尽可能小。基于此思想[17],下面给出区间二元语义偏差的定义。 (2) 而对于权重信息完全未知的情形,偏差(Dev)可定义为 (3) (4) 的最优解。 定理1:上述模型(4)的最优解为 (5) (6) 类似的,对于权重信息完全未知的情形,相对偏差(Cov)亦可定义为 (7) (8) 2.3.2 决策步骤 (9) (10) (11) (12) Step5:计算各方案(Ai,i=1,2,…,m)关于理想解的相对贴近度μi,即 (13) Step6:按照定义2.3相对贴进度值愈大、方案愈优,对各方案进行排序。 某医院接收一冠状病毒患者,在无特效药的前提下只能选择仅有的4种治疗方案进行治疗:对症(状)治疗(A1),抑制或巩固性治疗(A2)、限制功能丧失治疗(A3)、预防并发症治疗(A4)。确定最佳治疗方案时需要综合考虑4个因素(属性):技术可行(G1)、术后康复(G2)、时间代价(G3)和资源配置(G4)。由于患者病情严重,医院紧急召集4位传染病专家{E1,E2,E3,E4}参与决策,专家们对应的权重向量为w=(0.2,0.35,0.2,0.25)T。根据实际需要,专家们选取7粒度语言术语集S={s1,s2,s3,s4,s5,s6,s7}={极差,差,较差,一般,较好,好,极好}中的语言术语或不确定语言变量对各方案关于各属性进行评价。其中,属性集对应的权重向量为ω=(0.3,0.3,0.2,0.2)T,各专家给出的决策矩阵如下。 下面应用本文决策方法,确定患者最佳治疗方案。 表1 专家E1给出的语言决策矩阵R(1) 表2 专家E2给出的语言决策矩阵R(2) 表3 专家E3给出的语言决策矩阵R(3) 表4 专家E4给出的语言决策矩阵R(4) Step1:根据公式(9),将决策矩阵R(k),(k=1,2,3,4)一致化为区间二元语义决策矩阵B(k), Step2:根据公式(10),将各专家的决策矩阵B(k),(k=1,2,3,4)集成为群体决策矩阵B, Step5:按公式(13),计算各方案关于理想解的相对贴近度μi,(i=1,2,3,4), μ1=0.46,μ2=0.81,μ3=0.39,μ4=0.36。 Step6:根据相对贴进度值的大小,对各方案排序有:A2≻A1≻A3≻A4,从而A2(抑制或巩固性治疗)为最优方案。 将文献[6,10-11,13-14]与本文决策方法从其适用范围(权重信息、属性信息)、信息集成(运算法则、决策方法)等方面进行对比,具体分析结果见表5。 从表5可知,本文方法与已有方法明显的不同之处在于:本文方法通过偏差最小化模型,客观地集成群体评价信息,适用于权重值为实数或完全未知且属性值为语言术语或不确定语言变量的多属性群决策问题,较文献[6,10-11,13-14]适用面更广。其次,本文基于最优化理论与方法,提出语言集成算法;较文献[10-11,13]基于语言运算法则构造集成算子,省去了确定语言运算法则的复杂环节,也避免语言评价信息在运算时出现违反直觉或越界的问题。再者,文献[14]基于目标规划模型与群体一致度自动迭代算法确定方案优先权重,与本文通过欧式距离测度构建偏差最小化模型均适应于群体意见分歧较大的群决策问题,但文献[14]中方法无法处理权重信息为实数且属性信息为不确定语言变量的情形。 表5 不同决策方法对比 本文针对属性权重和专家权重为实数或完全未知的语言型决策问题,提出一种基于区间二元语义距离测度的多属性群决策方法。该方法通过构建偏差最小化模型定义集成算法,避免了现有语言型运算法则存在的一些不足,使得评价结果愈加合理。以及通过定义备选方案间相对偏差与相对贴近度,给出一种语言排序新方法。理论分析与实例结果均表明所提方法是可行有效的。


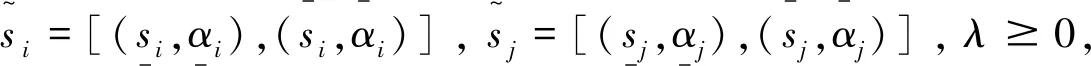

2 区间二元语义群决策理论与方法
2.1 基于距离测度的区间二元语义最小偏差法
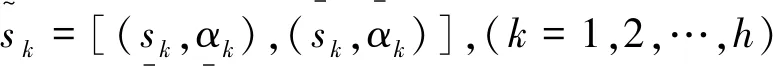

2.2 基于相对偏差和相对贴近度的区间二元语义排序方法


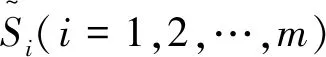
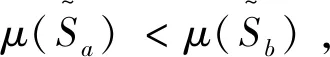

2.3 基于区间二元语义距离测度的多属性群决策方法
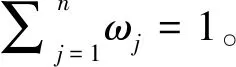




3 数值实例




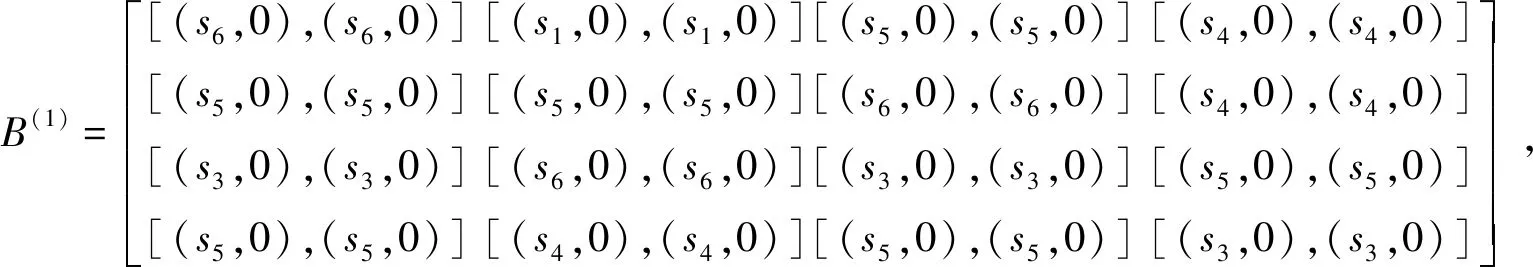

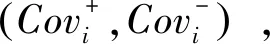
4 对比与分析
5 结论
