横向各向同性介质中用于井-地传输的电磁波的准确快速计算
2023-01-10梁朋飞真齐辉云喆付长民王若底青云
梁朋飞, 真齐辉, 云喆, 付长民, 王若, 底青云*
1 中国科学院深地资源装备技术工程实验室, 中国科学院地质与地球物理研究所, 北京 100029 2 中国科学院地球科学研究院, 北京 100029 3 中国科学院大学地球与行星科学学院, 北京 100049
0 引言
石油或天然气钻探的相关费用占石油天然气勘探总预算的60%之多(Zeng et al., 2018a),在钻探过程中,井下和地面之间的通信对于安全钻探和成功钻遇油气层至关重要(底青云等, 2021).井-地传输起到实时沟通井场和井下的作用:井下随钻测井仪器记录的数据,如温度、压力、速度、钻杆的姿态、钻杆附近电导率结构、速度结构,以及来自井场工程师的操作指令,均需要在地面和井下之间传输.井-地传输分为泥浆波传输和电磁波传输.泥浆波传输是20世纪70年代提出的一种井-地传输方法(Franconi et al., 2014),当前该技术成熟稳定,已在钻井中广泛使用.然而,泥浆波传输具有局限性,例如,它不能在生产井或不平衡钻井中使用(Franconi et al., 2014).因此,有学者提出了使用电磁波作为载波在井下和地面间实时传输数据(BéGuin et al., 2000; Hunziker and Maurer, 2000).均质和各向同性的模型首先用来模拟井-地电磁传输(Xia and Chen, 1993).近年来,研究人员基于分层的各向同性介质对井-地电磁传输进行了模拟(Yang et al., 2009; Chen et al., 2017; Zeng et al., 2018b; Liang et al., 2020).Chen等(2017)使用有限元方法模拟各向同性介质中的井-地电磁传输,Zeng等(2018b)和Liang等(2020)使用积分方程(IE)方法与矩量法(MoM)进行模拟.积分方程法和矩量法还可用来估计高电导率的套管对各向同性模型表面测量的电磁场的影响(Swidinsky et al., 2013; Tang et al., 2015; Patzer et al., 2017; Kohnke et al., 2018; Orujov et al., 2020).然而,钻探过程多会遇到横向各向同性(TI)介质,其对电磁场影响比较显著(Wang et al., 2009; Wang and Abubakar, 2018).Zeng等(2018b)提出了一种在横向各向同性介质中模拟井-地电磁传输的算法:采用三角函数作为矩量法的基函数,并采用数值方法对核函数及其积分进行近似计算.
本文提出了一种替代方法来模拟横向各向同性介质中的井-地电磁传输,为我国井-地电磁传输相关仪器的设计、开发提供支持.与前人方法相比,本文方法使用脉冲基函数,核函数具有解析形式,避免了前人方法中使用复杂的数值方法来计算核函数.本文的方法通过与横向各向同性介质中的数值解的比较,验证了该方法正确性,同时讨论了频率、钻杆的电导率、异常体层或目标层的各向同性或横向各向同性介质对钻杆上电流分布、地面电压信号的影响.此外,在设计仪器时该方法有助于在提高接收信号信噪比、选择最佳载波频率等方面进行模拟优化,并可随着钻井深度的增加优化传输数据的带宽.
1 理论背景
图1是含垂直钻杆的分层模型中的井-地传输示意图,第n层的下边界表示为zn+1,上边界表示为zn,σt n为该层的横向电导率,σzn是该层的垂直电导率.与周围横向各向同性模型的电导率相比,钻杆通常具有各向同性的高电导率(105~107S·m-1).横向各向同性(TI)模型各层的电导率包含在各层的有效介电常数中,其横向分量表示为:
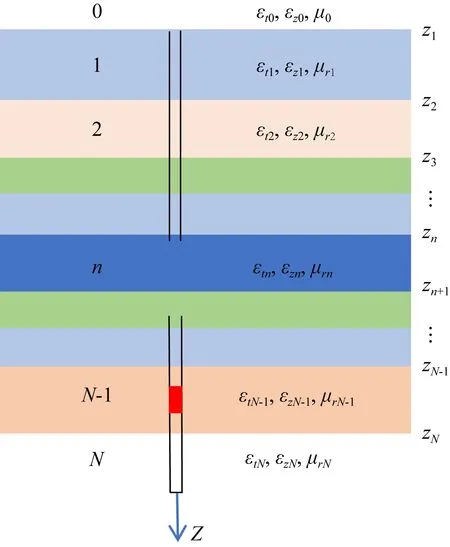
图1 含有垂直钻杆的层状横向各向同性模型中的井-地电磁传输系统示意图
(1)
垂直分量则表示为:
(2)
其中,εr n是第n层的相对介电常数,ω是角频率,ε0是自由空间的介电常数,j是复数单位.TI模型中各层的特征阻抗表示为:
(3)
其中相应的波数为
(4)
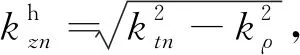
(5)
(6)
μ0是自由空间的磁导率,kρ是汉克尔变换的径向波数,上标e和h分别表示横向磁场和横向电场偏振.
图1中红色块体表示钻头附近的绝缘短节,其两侧加载电源激励一次场,钻杆及其周围的横向各向同性地层模型中因感应产生散射电磁场.由于钻杆的长度和电磁场的波长远远大于钻杆的半径,为方便散射电磁场的模拟,假设:(1)钻杆上的电流近似表示为线电流;(2)线电流仅沿钻杆轴向分布(Harrington, 1993).电磁波井-地传输模拟过程中使用矩量法,钻杆通常被离散成若干段,每段被视为一个电偶极子,因此,地面测量的电磁场是由钻杆上每个电流偶极子段激发的电磁场的叠加.钻杆辐射的散射电磁场和在分层模型中传播的散射电磁场可以用电场积分方程(EFIE)法来表示,其中用格林函数GA(r,r′)和相应的标量电位KΦ(r,r′)和Pz(r,r′)来表达电磁场,其表达式仅与模型参数有关(Liang et al., 2020).电磁场在钻杆表面满足以下边界条件:
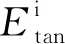
(7)

我们在式(7)的两边应用带有狄拉克权函数的点匹配方法得到:
(8)
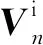
2 数值模拟
三层TI介质如图2所示,通过比较第1节所介绍方法的计算结果与COMSOL的模拟结果,检验本文方法的正确性.图2中,模型从上到下各层的厚度分别为400 m、600 m和半空间,横向电导率分量从上到下分别为0.5 S·m-1、0.1 S·m-1和0.05 S·m-1,纵向电导率分量从上到下分别为0.1 S·m-1、0.02 S·m-1和0.01 S·m-1,模型上方为一各向同性的半空间空气层,电导率为10-9S·m-1.一根垂直钻杆(长度为1000 m,半径为12.7 cm,电导率为105S·m-1)穿透TI介质模型,位于960 m深度处的绝缘短节(红色块)长度1 m,其两侧加载1 A的电流,频率为5.0 Hz.
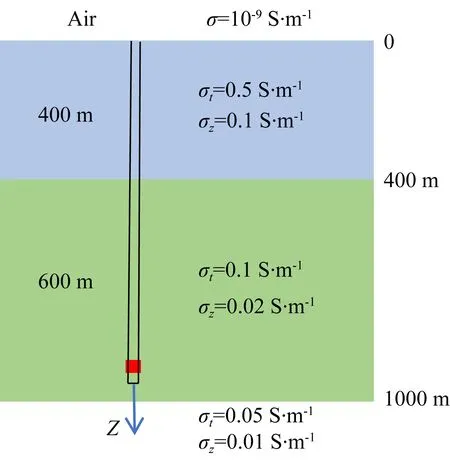
图2 井-地电磁传输系统模拟时使用的含有垂直钻杆的TI模型
图3显示了使用第1节所介绍的方法和COMSOL软件计算的沿钻杆的电流分布,红线为本文方法计算的结果,黑线为COMSOL软件的计算结果,两方法的计算结果吻合得很好.表1显示,本文方法的计算时间和内存消耗均低于COMSOL软件,表明该方法可以准确、高效地估计横向各向同性介质模型中的井-地电磁传输.此外,钻杆上分布的电流的大小和相位在400 m深度的边界处的变化趋势明显不同,表明横向各向同性介质模型中介质边界可以用电流分布的变化趋势来区分.
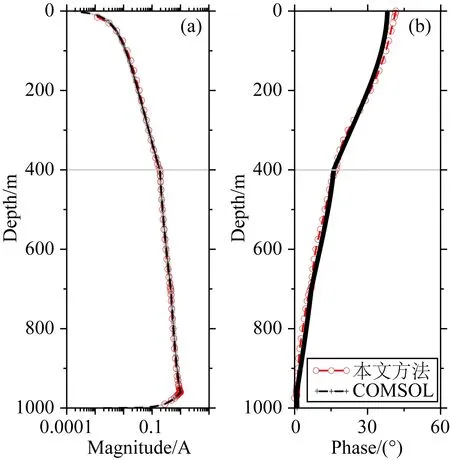
图3 沿着钻杆分布的电流大小(a)及其相位(b)
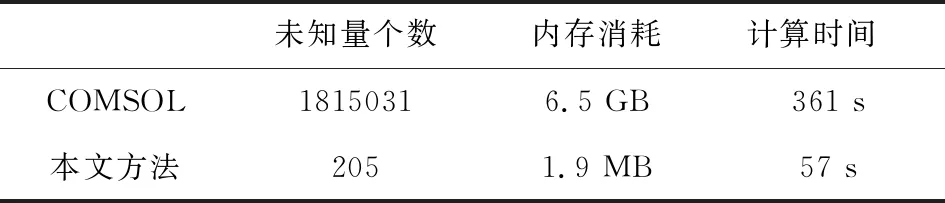
表1 COMSOL软件和本文方法计算时间和内存消耗
3 结果和讨论
3.1 钻杆电导率的影响
尽管为了简化建模而将有限电导率的钻杆视为理想导体(PEC),但真实钻杆的电导率对其上电流分布和电磁场的影响并不能忽视(Degauque and Grudzinski, 1987).这里讨论了TI模型中钻杆电导率(105~107S·m-1)对其上电流分布和地面接收电压(接收电压是钻杆头和模型表面上沿X轴某点之间的电压降)的影响.设计一个TI介质模型A,电导率的横向和纵向分量分别为0.05 S·m-1和0.01 S·m-1,960 m的深度处有一个长度为1 m的绝缘短节,两侧加载电压1 V,频率为5 Hz.
图4和图5中,十字代表钻杆电导率为105S·m-1时其上电流的分布,菱形为107S·m-1的情形,黑色为各向同性电导率模型(σt=σz=0.01 S·m-1)的情形,红色为TI介质(σt=0.05 S·m-1,σz=0.01 S·m-1)的情形,蓝色为各向同性的电导率模型(σt=σz=0.05 S·m-1)的情形.图4显示,在TI介质中,沿着电导率为105S·m-1和107S·m-1的钻杆上的电流大小明显不同,特别是在远离源的位置处,差异变大;而钻杆上电流的相位差异则更明显,但它不受与源的距离远近影响.同时,在各向同性的模型中也有相同的趋势,即当钻杆的电导率增加时,沿钻杆上分布的电流大小会增加.并且,当钻杆的电导率从105S·m-1变为107S·m-1时,一个各向同性(0.05 S·m-1)或TI模型与另一个各向同性模型(0.01 S·m-1)之间的电流差异(幅度和相位)明显增加,这揭示了具有较高电导率的钻杆能提高源的辐射效率.最后,TI模型(σt=0.05 S·m-1,σz=0.01 S·m-1)中钻杆上的电流在两个各向同性模型(σt=σz=0.01 S·m-1和σt=σz=0.05 S·m-1)中钻杆上电流的变化范围内变化,这也从侧面揭示了本文方法的有效性.

图4 沿着钻杆分布的电流大小(a)及其相位(b)
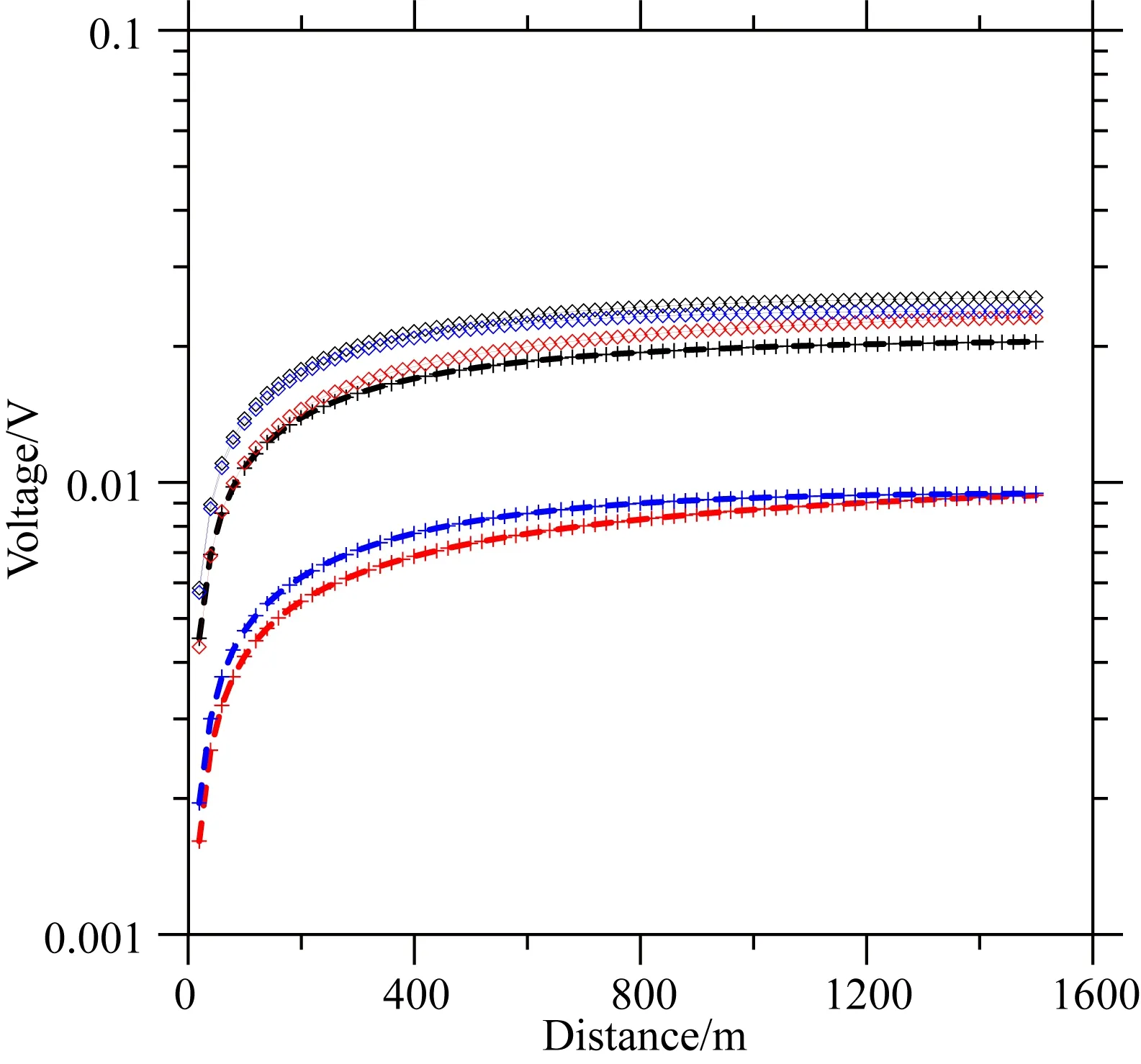
图5 地面接收的电压信号随与钻杆距离的变化
图5显示,含有不同电导率钻杆的模型,地面的电压信号明显不同:含较高电导率(107S·m-1)的钻杆的模型(各向同性或TI模型)的地面观测电压高于具有较低电导率钻杆(105S·m-1)的模型表面观测的电压,这也表明具有较高电导率的钻杆比具有较低电导率的钻杆的辐射效率高.图5还显示,尽管低电导率钻杆上的电流比高电导率钻杆上的电流要小,然而具有低电导率的各向同性(0.01 S·m-1)模型表面激发的电压略高于另一个具有高电导率的模型(σt=σz=0.05 S·m-1或σt=0.05 S·m-1,σz=0.01 S·m-1),原因是较高的地层电导率会导致电磁场衰减得更快,在地面接收到较小的电压信号.相反,在一个含电导率为105S·m-1钻杆的各向同性的低电导率(0.01 S·m-1)的模型表面观测的电压要比另一个具有高电导率的模型(σt=σz=0.05 S·m-1或σt=0.05 S·m-1,σz=0.01 S·m-1)表面的电压要高许多,这是由不同电导率钻杆的激励效率的差异造成的.当钻杆的电导率从105S·m-1增加到107S·m-1时,高电导率模型(σt=σz=0.05 S·m-1或σt=0.05 S·m-1,σz=0.01 S·m-1)和低电导率模型(0.01 S·m-1)中钻杆上电流分布的差异变得明显.以上分析表明:有限电导率的钻杆对其上的电流分布和接收的电压信号有明显的影响,钻杆的高电导率有利于提高辐射源的辐射效率.
3.2 TI介质模型的影响
通过比较TI模型和各向同性模型(电导率为0.01 S·m-1或0.05 S·m-1)的响应,测试介质的电导率对地面接收信号的影响.TI模型各层的横向导电率为0.05 S·m-1,垂直导电率为0.01 S·m-1,各向同性模型的导电率为0.01 S·m-1或0.05 S·m-1,半空间层电导率为0.01 S·m-1或0.05 S·m-1,其他参数与模型A相同.
图6和图7中,黑线和绿线分别是具有各向同性电导率(0.01 S·m-1或0.05 S·m-1)的模型中钻杆上的电流分布,红线和蓝线是TI模型(σt,σz)=(0.05, 0.01) S·m-1的情形.图6显示,具有高电导率(0.05 S·m-1)半空间层的TI模型中钻杆上电流分布与电导率为0.05 S·m-1的各向同性模型中钻杆上电流分布一致,但另一个具有低电导率(0.01 S·m-1)半空间层的TI模型与具有电导率(0.05 S·m-1)各向同性模型的电流分布差异显著,这两个模型与另一个各向同性模型(0.01 S·m-1)中钻杆上的电流分布也有明显差异.因此,可得出电流分布对TI介质的垂直电导率分量的变化不敏感,但对横向电导率分量的变化敏感.图7显示,电压随与钻头的距离增大而增加;当两者的距离进一步增加时,电压趋于保持在一定的水平,这一特点有助于优化观测点的位置,以观测到具有较高信噪比的信号.此外,黑线与红线的差异表明接收到的电压信号对模型横向电导率分量的变化比纵向电导率分量的变化更敏感.

图6 沿着钻杆分布的电流大小(a)及其相位(b)
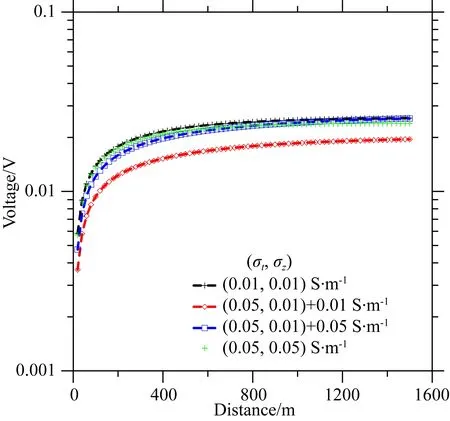
图7 地面接收的电压信号随与钻杆距离的变化
3.3 频率的影响
频率是影响电磁波响应的另一个重要参数,这里比较了TI模型与各向同性模型在5 Hz和100 Hz时钻杆上的电流分布、地面观测的电压信号.各向同性的模型中每层的横向和纵向电导率均为0.01 S·m-1或0.05 S·m-1,而TI模型每层的横向电导率为0.05 S·m-1,纵向电导率为0.01 S·m-1,其他参数与模型A相同.
图8和图9中,十字代表频率为100 Hz时钻杆上电流分布,菱形代表频率为5 Hz的情形,黑色代表各向同性模型(σt=σz=0.01 S·m-1)的钻杆上电流分布,红色是TI模型(σt=0.05 S·m-1,σz=0.01 S·m-1)的情形,蓝色是另一各向同性模型(σt=σz=0.05 S·m-1)的情形.图8显示,在导电性强(σt=σz=0.05 S·m-1或σt=0.05 S·m-1,σz=0.01 S·m-1)的模型中,钻杆上电流的大小对工作频率的变化比低电导率模型(σt=σz=0.01 S·m-1)更敏感,特别是在远离源的位置.这是因为高电导率模型中电磁波衰减变化更剧烈.图8还显示,在电导率相同的情况下,无论位置是靠近还是远离源,电流相位均对频率的变化敏感.图9显示,在电导率相同的情况下,电压信号对频率的变化也敏感,并进一步显示,高频电磁波对模型的电导率的变化更敏感.由于高频率电磁波对于提高电磁传输系统的数据传输速率有帮助,因此,此方法有助于优选最佳的频率,在信号的高幅度和高传输率之间做一个平衡.
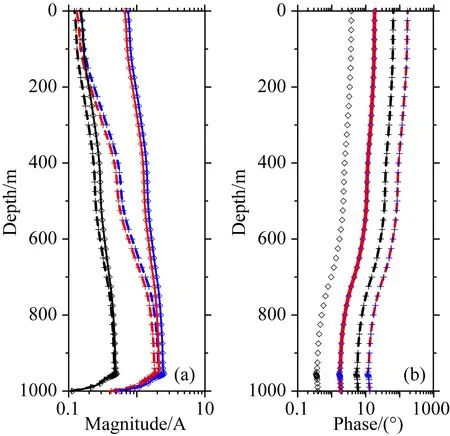
图8 沿着钻杆分布的电流大小(a)和相位(b)

图9 地面接收的电压信号随与钻杆距离的变化
3.4 TI层的影响
为了测试TI电导率层对观测信号的影响,将模型A的第一层设置为TI电导率层,(σt,σz)=(0.05, 0.01) S·m-1,第二和第三层均为各向同性电导率层,电导率相同,为0.01 S·m-1或0.05 S·m-1.
图10和图11中,黑线和绿线分别是各向同性的电导率模型(0.01 S·m-1或0.05 S·m-1)中钻杆上的电流分布,红线是第一层为TI异常层、电导率为(σt,σz)=(0.05, 0.01) S·m-1以及底层的电导率为0.01 S·m-1(图11中Anm_0.01所示)的情形,蓝线是TI层和底层的电导率为0.05 S·m-1(图11中Anm_0.05所示)的情形.图10显示,具有TI层、且其他层电导率为0.01 S·m-1或0.05 S·m-1的模型中钻杆上的电流大小在电导率为0.01 S·m-1和0.05 S·m-1的各向同性模型中钻杆上电流的变化范围之内变化,从侧面验证了方法的正确性.此外,第一层为TI介质、第二层电导率为各向同性介质(0.01 S·m-1)的模型中,第一层中钻杆上电流(大小和相位)分布趋于接近电导率为0.05 S·m-1的各向同性介质的情形,而第二层中钻杆上的电流分布与电导率为0.01 S·m-1的各向同性介质相近;同时,另一个具有TI异常层、第二层电导率为0.05 S·m-1的模型中,第二层钻杆上激发的电流(大小和相位)与电导率为0.05 S·m-1的各向同性模型相近.这表明,当源位于低电导率层(0.01 S·m-1)时,TI异常层可能会降低钻杆上电流大小在同一层中钻杆上的衰减率,但当源位于高电导率层(0.05 S·m-1)时,此作用就不明显了;电流分布对横向电导率分量的变化很敏感,但对纵向电导率变化不敏感.
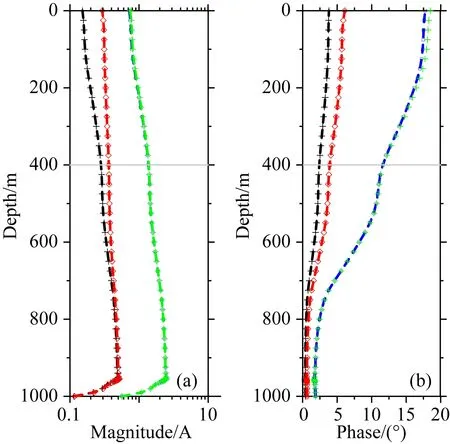
图10 沿着钻杆分布的电流大小(a)及其相位(b)
图11中蓝线和绿线对比显示,接收到的电压信号对模型的TI异常层中的纵向电导率变化不敏感,尽管在电导率为0.05 S·m-1模型中沿钻杆的电流比在电导率为0.01 S·m-1模型中的钻杆上的电流大,但电磁场在高电导率模型(0.05 S·m-1)中比在低电导率模型(0.01 S·m-1)中衰减得更快,最后两模型中观测到的电压可以达到相同的水平.此外,具有TI异常层和低电导率(0.01 S·m-1)层的模型接收到的信号比各向同性模型(0.01 S·m-1)接收到的信号小得多,这是因为存在电流的横向传导衰减,导致电磁场快速衰减,接收到的信号也小得多.
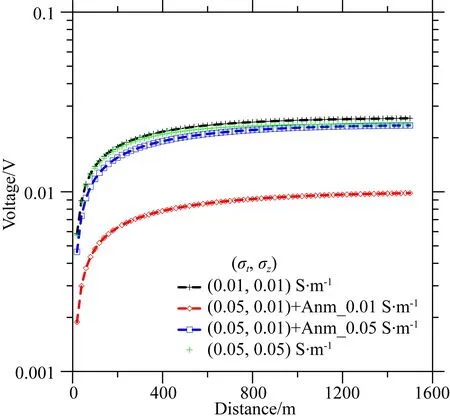
图11 地面接收的电压信号随与钻杆距离的变化
3.5 对目标层的敏感度
为了测试TI电导率目标层对观测信号的影响,将模型A的第二层和第三层设置为TI电导率层,电导率为(σt,σz)=(0.05, 0.01) S·m-1,第一层为各向同性电导率层,电导率为0.01 S·m-1或0.05 S·m-1.
图12和图13中,黑线和绿线分别是各向同性的电导率(0.01 S·m-1或0.05 S·m-1)模型中钻杆上的电流分布,红线是第二层为TI目标层、电导率为(σt,σz)=(0.05, 0.01) S·m-1以及顶层的电导率为0.01 S·m-1(图13中Tgt_0.01所示)的情形,蓝线是含TI目标层、顶层电导率为0.05 S·m-1(图13中Tgt_0.05所示)的情形.图12显示,具有TI目标层、顶层电导率为0.01 S·m-1或0.05 S·m-1模型的钻杆上电流的大小在电导率为0.01 S·m-1和0.05 S·m-1各向同性模型的钻杆上的电流变化范围内变化,从侧面验证了方法的正确性.此外,在第一层电导率为0.01 S·m-1、且含TI介质的模型中,第一层的电流(大小和相位)分布趋于接近电导率为0.01 S·m-1的各向同性介质中电流的分布,而第二层的分布则接近电导率为0.05 S·m-1的各向同性介质中钻杆上电流的分布.相反,另一个具有TI目标层、顶层电导率为0.05 S·m-1的模型中激发的电流(大小和相位)几乎与电导率为0.05 S·m-1的各向同性模型的情形相同.这个对比表明,周围的低电导率地层会导致电流的幅度沿着钻杆快速下降.此外,具有高电导率(0.05 S·m-1)TI目标层的模型(图12中的蓝线)与高电导率(0.05 S·m-1)各向同性模型(图12中的绿线)的差异比带有TI异常层模型(图10中的蓝线)和高电导率(0.05 S·m-1)各向同性模型中(图10中的绿线)之间的差异更明显,这归因于源的位置及其周围的介质的差异:因为此模型的源位于TI层,而其他模型的源则位于各向同性层中.

图12 沿着钻杆分布的电流大小(a)及其相位(b)
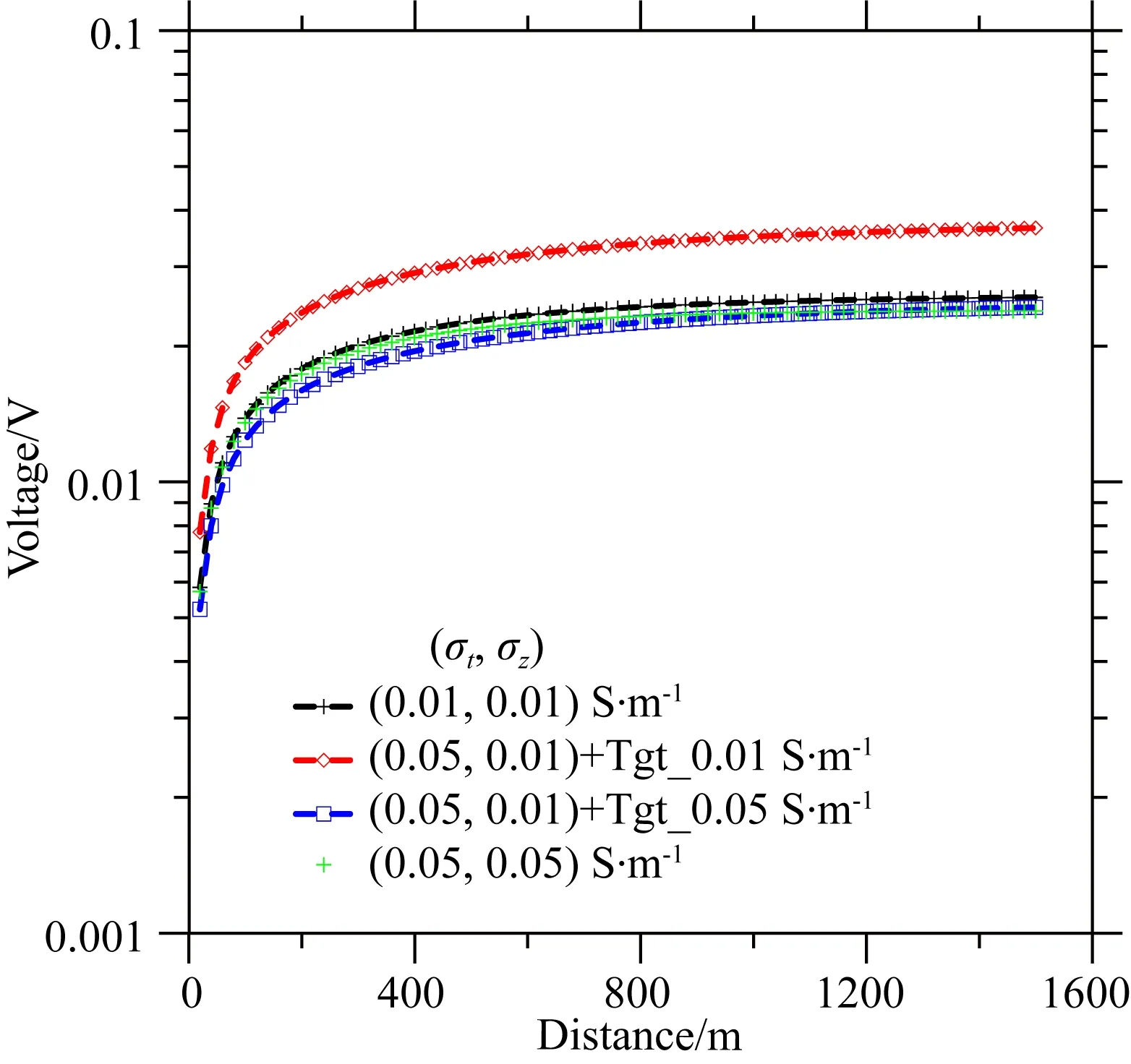
图13 地面接收的电压信号随与钻杆距离的变化
图13表明,接收信号对各向同性模型(0.05 S·m-1)或高电导率(0.05 S·m-1)层下面有TI目标层的模型的电导率的变化不敏感.此外,具有TI目标层和顶层低电导率(0.01 S·m-1)的模型的接收信号明显高于各向同性的模型(0.01 S·m-1),这是因为TI模型的目标层比各向同性的模型有更多的横向传播电磁波,最终导致含TI目标层在内的模型的电压信号更高.
4 结论
本文开发并验证了一种准确、快速地计算井-地电磁传输时,TI介质中电流沿钻杆的分布、地面接收信号的方法.该方法使用基于脉冲基函数和狄拉克加权函数的矩量法来离散钻杆上电流,基于积分方程法计算散射电磁场.该方法中,散射场的积分核具有解析形式,可精确求解,同时避免了前人方法中使用数值方法进行的复杂近似计算,具有精度高、计算效率高的特点.
计算结果表明,频率和钻杆的电导率对钻杆上电流分布以及模型表面电压信号有显著影响.该方法可用于优选最佳的辐射频率,平衡井-地电磁传输中数据高速传输和接收高信噪比信号对于频率选取的要求.高电导率的钻杆能提高源的辐射效率,钻杆周围高电导率地层会降低沿钻杆分布的电流的衰减率.钻杆上电流分布和接收信号对地层电导率的横向分量比垂直分量更敏感.TI异常层和TI目标层对电流分布和电压信号有不同的影响:带有TI异常层的模型会激发相对较弱的电压信号,但带有TI目标层的模型会激发相对较强的电压信号.
