基于改进Frequency-Bessel变换法的主动源Love波频散分析

张凯， 王小江*， 刘建勋， 王凯， 姜春香

1 中国地质科学院地球物理地球化学勘查研究所， 廊坊 065000 2 国家现代地质勘查工程技术研究中心， 廊坊 065000

0 引言

横波速度信息及其动力学特征是岩土基本物理性质之一，它与岩土岩性、孔隙度、密度及孔隙流体的性质等参数有直接关系.面波多道分析技术(Multichannel Analysis of Surface Waves，MASW)由于其非侵入性、高效、低成本、空间采样广以及精度较高等优势，在获取浅地表横波速度结构方面获得了广泛应用(Song et al., 1989; Park et al., 1999; Xia et al., 1999；刘耀徽等，2021；陈淼等，2022).该方法首先对面波记录进行频散分析，然后从中提取面波频散曲线，最后基于面波频散曲线的正演计算，进而反演得到地表下一维横波速度结构，该一维横波速度结构代表多道平均的结果(Luo et al., 2009).面波频散分析是面波多道分析技术中至关重要的一环，对面波进行频散谱分析，需要将地震波场从时间-空间域变换到频率-相速度域.为了提高频散谱成像的分辨率和可靠性，国内外学者提出以下几种比较常见的频散分析方法：τ-p变换(McMechan and Yedlin, 1981)、频率波数变换算法(f-k变换方法)(Gabriels et al., 1987; Yilmaz, 2001)、相移法(Park et al., 1998)、频率分解倾斜叠加法(Xia et al., 2007)，高分辨率线性Radon变换法(Luo et al., 2008).

与Rayleigh波相比，Love波相速度不受纵波速度影响(Aki and Richards, 2002)，其反演参数较少，可使反演过程更加稳定、求解的横波速度更加可靠.Luo等(2010)利用有限差分模拟高频Love波，分析了层状模型中Love波的传播和频散特征.Xia等(2012, 2013)提出Love波多道分析方法(Multichannel Analysis of Love Waves)，与MASW类似，对Love波数据进行分析从而获得浅地表SH波速度模型.Love波的频散曲线比Rayleigh波的简单，基阶Love波勘探深度较浅，但相同阶数的高阶Rayleigh波和Love波勘探深度相当(Yin et al., 2014).场地试验表明，地震记录中Love波的连续性和线性性较好，与Rayleigh波相比，Love波频散能量谱通常更加清晰，并具有更高的分辨率，同时频带更宽，从而提高了频散曲线的拾取精度和反演结果的可靠性(夏江海等, 2015).此外，Rayleigh波和Love波联合勘探可以进一步减少反演的多解性，提升横波速度模型精度(Dal Moro et al., 2015; Yin et al., 2020).

当前，利用Frequency-Bessel变换方法从背景噪声中提取多阶面波频散曲线得到越来越多的关注和应用(Wang et al., 2019; Hu et al., 2020; Xi et al., 2021).杨振涛等(2019)将该方法用于主动源Rayleigh波频散分析，称之为矢量波数变换法.与相移法相比，矢量波数法能够获得高分辨率的多阶Rayleigh波频散谱，具其抗噪性更好(苏悦等, 2020).Forbriger(2003)指出利用0阶和1阶Frequency-Bessel变换可以分别得到Rayleigh波垂直分量(ZZ分量)和径向分量(ZR分量)的频散能量图.Hu等(2020)利用Frequency-Bessel变换方法从多分量背景噪声数据中提取Rayleigh波和Love波频散曲线，通过互相关函数RR和TT(切向)两个分量相加或相减以保持结果中只含有0阶或者2阶贝塞尔函数，然后利用0阶和2阶Frequency-Bessel变换得到对应的频散谱，进而实现Rayleigh波和Love波的分离.席超强(2021)根据贝塞尔函数的性质通过数值分析对比得出，RR分量的0阶Frequency-Bessel变换只对Rayleigh波敏感，而对Love波不敏感；同样的，TT分量的0阶Frequency-Bessel变换只对Love波敏感，而对Rayleigh波不敏感.与背景噪声互相关函数RR或者TT分量中同时含有Rayleigh波和Love波组分不同，由于震源方向的可控性，主动源TT分量一般只含有Love波组分，然而就目前作者所知，并没有相关文献给出完整的主动源Love波Frequency-Bessel变换频散分析方法.因此，本文利用改进Frequency-Bessel变换法提取主动源Love波频散曲线，并通过数值模拟和实例测试表明，该方法具有较高的分辨率和多阶分辨能力，为多分量面波勘探提供一种有效的频散分析手段.

1 理论研究

本文使用如下的Fourier正反变换约定形式：

(1)

(2)

1.1 刚度矩阵法

刚度矩阵法(Stiffness Matrix Method)是有限元法的一种，通过建立单个层状板的位移应力关系，然后将单元刚度矩阵集合成整体层状模型的全局刚度矩阵，达到分析整体模型波场位移的目的.对于N层半空间，自由表面为第一层界面，第N个界面下方为无限半空间，则第l层的刚度矩阵为：

(3)

对于SV-P分量，Kl由四个2×2的子矩阵组成，其各个元素与第l层的纵波速度VP、横波速度VS、密度和层厚h参数有关.在考虑介质衰减的情况下，本文采用恒定Q值(纵横波品质因子QP和QS)模型，则对应的速度变为复数值，取其一阶近似有：c=V(1+i/2Q).模型底部半空间的刚度矩阵Khalfspace缩减为2×2的矩阵.对于SH分量，Kl为2×2矩阵，其四个元素与层横波速度、密度和层厚参数有关.此时模型底部半空间对应的刚度矩阵Khalfspace只包含一个元素.详细的刚度矩阵关系公式可参考Kausel(2006)书里的表1 0.1，在此不再一一列出.

将各个层的刚度矩阵叠加起来，即重合部分的元素加和在一起组成三对角矩阵，即为全局刚度矩阵.以五层半空间模型(图1)为例有：

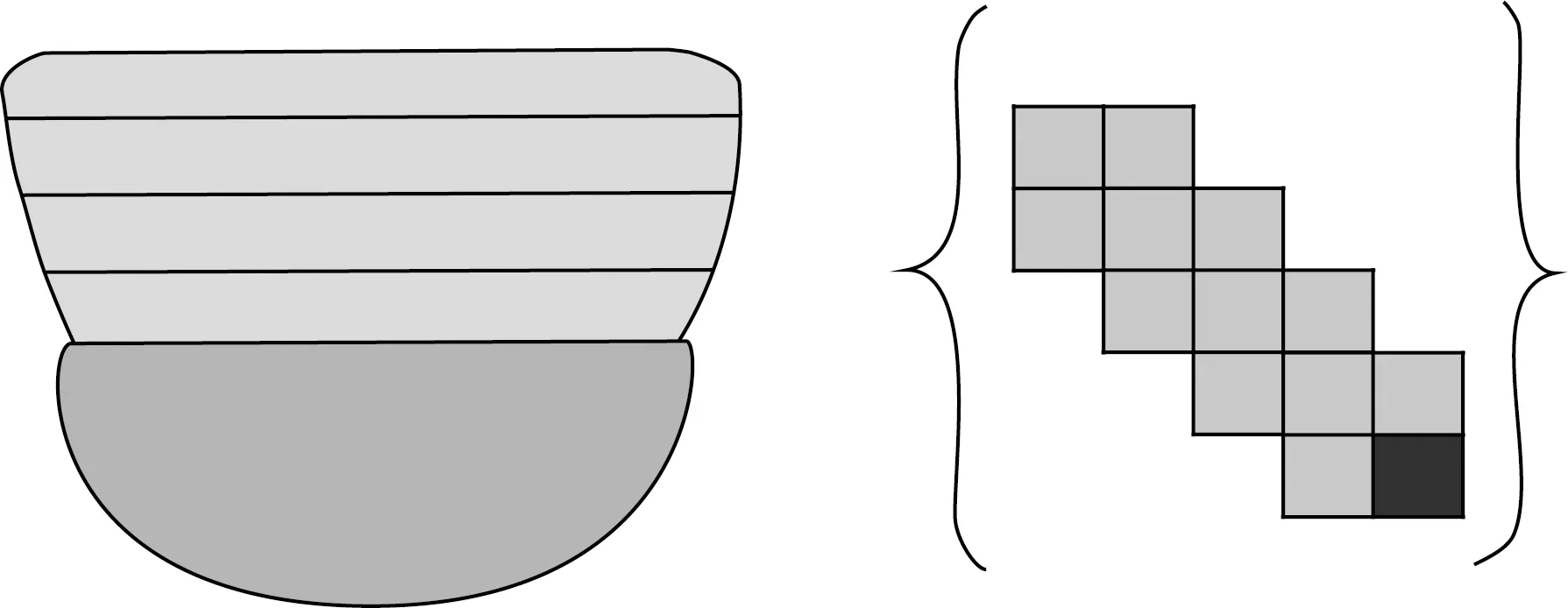
图1 五层半空间模型及其全局刚度矩阵示意图(Kausel, 2017)

(4)

求得全局刚度矩阵后，即可根据各个层上的外力荷载与位移的线性关系P=Ku，求解波数域位移矢量u=K-1P.对于N层半空间，展开有：

(5)

对于震源和接收点都在自由表面的情况，则有：

(6)

G(k,ω)表示波场在频率域和波数域的谱系数，当震源和接收点位于同一深度时，gZR等于gRZ.这里我们将gZZ、gZR和gTT分别称为垂向、垂径向和切向格林函数谱，也即对应Rayleigh波垂向、径向分量和Love波的本征谱.另外，我们把gRR称为径向格林函数谱.对于弹性介质，当k等于Rayleigh波特征值时，gZZ、gZR、gRZ和gRR在理论上为无穷大值；而当k等于Love波特征值时，gTT在理论上为无穷大值.

1.2 Frequency-Bessel变换法

Frequency-Bessel正变换和逆变换互为对称(又称Fourier-Bessel变换)：

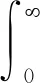
(7)

(8)

式中，n为整数，Jn为第一类n阶贝塞尔函数.

柱坐标下，空间域格林函数与波数域格林函数谱的关系如下(Kausel, 2006)：

垂直点力源下的径向分量和垂直分量分别为：

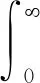
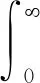
(9)

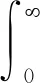
(10)

水平点力源下的径向分量、切向分量以及垂直分量分别为：

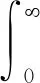
-gRR(k)J1(kr)/kr]kdk，

(11)

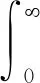
-gTT(k)J1(kr)/kr]kdk，

(12)

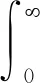
(13)

对于主动源面波勘探来说，式(9)、式(10)和式(12)为常用的三个分量，分别代表Rayleigh波径向分量、Rayleigh波垂直分量以及Love波分量.当模型已知时，通过Frequency-Bessel逆变换在波数域k对格林函数谱进行积分即可得空间域格林函数.反之，已知格林函数，通过Frequency-Bessel变换在空间域r对格林函数进行积分即可得波数域格林函数谱，从而求解出频散能量谱.实际上，对空间域的采样是一系列有限的离散点，可以采用对格林函数进行线性插值的方法(Wang et al., 2019)或者梯形积分法(Hu et al., 2020)求解空间域积分，本文采用快速简单且足够精确的梯形积分法.

对Rayleigh波径向分量和垂直分量分别进行1阶和0阶Frequency-Bessel变换可以得到其对应的格林函数谱.然而对于切向Love波分量，式(12)中不仅包含径向和切向格林函数谱，还含有0阶和1阶贝塞尔函数.对式(12)进行0阶Frequency-Bessel变换有：

(14)

其中kL代表给定的Love波波数，式(14)可以分为两部分，分别为：

(15)

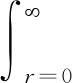
×J0(kLr)dr，

(16)

变量k、r相互独立，交换积分次序，并根据同阶贝塞尔函数的正交性，可得：

(17)

-gTT(k)]dk.

(18)

根据贝塞尔函数积分性质：

(19)

不失一般性，忽略掉k=kL时因子1/2的差异，代入式(18)可得：

(20)

考虑当k很大时，刚度矩阵不仅解耦为块对角矩阵，还收敛到对应的静态解(Kausel, 2018)，即当k→∞,格林函数谱G11(k,ω)收敛为：

(21)

(22)

(23)

取kmax为分界点，当k>kmax时，将式(21)和式(22)代入式(20)得：

(24)

实际数值计算中，kmax的取值由公式(25)给出(Kausel, 2018)：

(25)

对于弹性介质，当k等于Love波波数本征值时，gTT(k)趋向于无穷大，而当k等于Rayleigh波波数本征值时，gRR(k)趋向于无穷大.剔除掉区间[kL,kmax]中所有的面波波数本征值，可得：

(26)

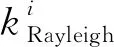
由式(17)和式(26)可以看出，对Love波分量进行0阶Frequency-Bessel变换，得到的是径向格林函数谱(Love波频散谱)与I2之和.当kL等于Love波波数本征值时，I1项为无限大，而I2中全部四项的和为一有限值，因此通过扫描不同的kL值，I(kL)的极大值即对应Love波频散曲线.

对于黏弹性模型，介质的衰减会使格林函数谱中的奇点消失，在面波特征值处的无穷大值变为有限值，此时可直接通过式(24)计算I2.我们以二层模型为例(表1)，对于给定的频率-波数对(ω，kL)，分别计算I1和I2，图2分别给出10 Hz、20 Hz、30 Hz和50 Hz不同频率下位移切向分量的0阶Frequency-Bessel变换与切向格林函数谱的对比结果(两者虚部)，结果显示两者差异总体较小，尤其在极大值处两者基本一致，都等于Love波理论相速度(图2中蓝色实线).面波理论相速度由快速delta矩阵算法给出(Buchen and Ben-Hador, 1996; Wu et al., 2019).因此，利用0阶Frequency-Bessel变换可以有效获取Love波频散特征.

图2 不同频率下位移切向分量的0阶Frequency-Bessel变换与切向格林函数谱对比图

表1 二层层状模型的地层参数

1.3 改进Frequency-Bessel变换法

采用离散波数法(Bouchon, 2003; Kausel, 2018)模拟点源引起的地震波场记录，模拟的炮集记录偏移距5 m，排列长度200 m，道间距5 m.对地震波场记录进行Frequency-Bessel变换得到的面波频散能量图会产生“交叉”假频(图3a)，将贝塞尔函数分为第一类Hankel函数和第二类Hankel函数两部分，即：

(27)

这两部分分别描述了二维波动方程的内行柱面波解和外行柱面波解，因此Frequency-Bessel变换可以理解为在正方向(+k)和负方向(-k)上分别对波场进行速度扫描.这与利用相移法(Park et al., 1998)对同时含有正向和反向炮集记录的波场进行速度扫描而产生的“交叉”假频类似.假频所对应的波数与道间距dx成反比，且具有周期性，他们之间关系如下(Cheng et al., 2018; Xi et al., 2021; Zhou and Chen, 2022)：

k0=M/2dx,M=1,…N.

(28)

仅利用第一类Hankel函数在正方向(+k)上对波场记录进行速度扫描将会避免“交叉”假频的产生(Forbriger, 2003)，同时又能给出足够精确的面波频散谱.图3b为仅利用第一类Hankel函数对波场进行速度扫描后的结果，假频消除后，频散能量更清晰连续，有利于拾取更高频段的频散曲线.该方法被称为改进Frequency-Bessel变换法(Xi et al., 2021).值得注意的是，由于Fourier正反变换约定形式的不同，Forbriger(2003)给出的正向速度扫描对应的是第二类Hankel函数.

图3 二层弹性模型Love波频散能量图

综上所述，对于主动源面波勘探，可以利用0阶或1阶Frequency-Bessel变换获得面波频散能量图，通过求取图中极大值的位置可以获得面波的相速度值.具体公式如下：

(29)

2 实例分析

我们在雄安新区南部高阳县孝义河河堤土路上开展了Love波场地试验(图4a).Love波由锤击垂直于排列的木枕产生.为加强木桩与地面的耦合，将多根并排钢钎贯穿桩体并插入地下，激发时多人站在木桩上以增加配重.木桩长轴方向和锤击方向均与检波器方向一致(同垂直于测线方向)，每个测点同方向敲击5次.水平检波器主频为4 Hz，道距dx为2 m，最小偏移距为10 m，排列长度90 m，采样率为0.5 ms，采样长度1 s.

图4b、c分别代表在相距120 m的两个测点L1和L2处采集的多道地震记录，Love波较发育，信噪比较高.图5a、b代表由相移法生成的频散能量图，图5c、d代表由改进Frequency-Bessel变换法生成的频散能量图.图中黑点为根据相移法生成的频散能量图中每个频点的峰值自动拾取的频散曲线.图中黑色虚线代表线性排列能分辨的最大波长，即直线v/f=100 m.由于道距较小，根据Nyquist定理，最大波数为Nyquist波数的两倍，为1/dx，也即能分辨的最小波长等于dx(Cheng and Xia, 2022).由此可知，图5中拾取的频散曲线并不会受到空间采样假频的干扰.需要说明的是，为便于描述，我们简单地按照速度值的大小依次给定频散曲线的阶数，并不考虑面波频散曲线阶数误标的问题.对比图5a、c，改进Frequency-Bessel变换法对Love波第二高阶模式的成像更加清晰连续.同样的，对比图5b、d，改进Frequency-Bessel变换法对Love波第一和第二高阶模式的成像更加清晰连续.我们分别提取了图5a、c中基阶和第一高阶的频散曲线，如图6a所示，两者虽然存在偏差，但两者的平均差值为1.547 m·s-1，最大差值为4 Hz低频端，其值为21.8 m·s-1，这是由于低频段频散能量旁瓣较大，导致误差偏大.而第一高阶两者的最大偏差为4.9 m·s-1，最大相对误差为2.68%，因此，两种方法对Love波基阶和第一高阶的成像结果基本一致.同样的，对于测点L2，由图6b可知两种方法对Love波基阶和第一高阶的频散曲线提取结果基本一致.

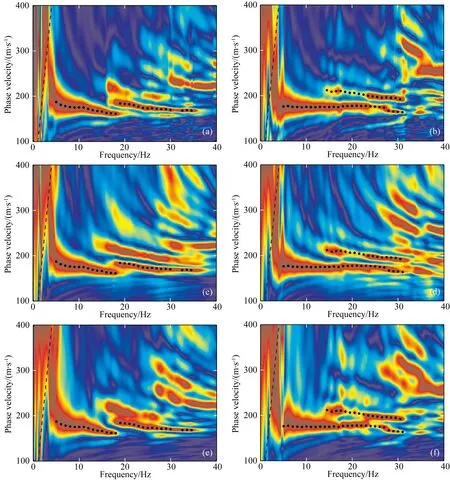
图5 相移法，改进Frequency-Bessel变换法生成的频散能量图和利用改进Frequency-Bessel变换法对经时间域归一化后的Love波多道地震记录进行频散分析的结果

图6 利用相移法和改进Frequency-Bessel变换法提取的频散曲线对比结果

一般地，面波频散分析前需要对原始炮集记录进行时间域归一化，由于相移法只关注相位信息，在对原始炮集记录做Fourier变换后，其振幅谱并没有参与频散分析计算，因此在利用相移法对时间域地震记录进行频散分析前不必进行时间域归一化.而改进Frequency-Bessel变换法同时利用到原始炮集记录的振幅谱和相位谱，因此时间域归一化可能会对该方法的频散分析结果产生影响.图5e、f分别代表L1和L2两个测点地震记录经各道时间域归一化后由改进Frequency-Bessel变换法生成的频散能量图.通过与图5c、d对比可以看出，由于时间域归一化改变了原始地震信号的振幅谱，导致L1测点第二高阶和L2测点第一高阶只在较窄的频带范围内能量较强，其频散能量整体连续性相对较差.另外，时间域归一化使得基阶频散能量峰值整体有所偏高.为保证尽量好的频散分析效果，在实际应用中，我们建议利用改进Frequency-Bessel变换法对原始炮集记录和经时间归一化后的炮集记录分别进行频散分析，挑选较好的频散分析结果用作后续面波反演.

3 讨论

在实际应用中，采集的地震记录不可避免会含有一定的噪声，从而影响频散谱的成像质量，因此有必要对Frequency-Bessel变换方法进行抗噪性测试.以二层层状模型为例(表1)，我们将20%和50%的随机噪声加入理论模拟的地震数据(图7a、b)，噪声的计算公式为：

图7 (a)和(b)分别代表含20%和50%随机噪声的模拟地震记录；(c)和(d)分别代表对应的由相移法生成的频散能量图；(e)和(f)分别代表对应的由改进Frequency-Bessel变换法生成的频散能量图，黑点代表Love波理论频散曲线

Data=Signal+2×(0.5-RND)

×mean(max(Signal))×Noise,

(30)

其中Data代表含有噪声的数据，Signal代表模拟地震数据，Noise代表噪声水平，mean(max(Signal))代表地震记录各道最大值的平均值.图7c、e分别代表由相移法和改进Frequency-Bessel变换法生成的频散能量图.图中黑点代表Love波理论频散曲线.可以看出，由于噪声高频干扰，导致在高频段(>40 Hz)几乎无法获取有效的频散信息.相比含20%噪声的情况，含50%噪声的地震记录所对应的频散能量谱在高频受到的干扰更多，其有效频带范围更窄.对比7c、d和图7e、f可知，改进Frequency-Bessel变换法的抗噪能力要优于相移法.以上只测试了随机噪声对频散谱成像质量的影响，然而实际上噪声来源各种各样，进而产生多种类型的假频干扰(对这些假频进行系统性的梳理可参考相关文章(Cheng and Xia, 2022)).因此，在实际应用中，应测试多种频散分析方法，选取其中较好的一种方法或多种方法组合.从这种意义上来看，Frequency-Bessel变换法提供了一种新的可供选择的面波频散分析手段.

4 结论

为提高主动源Love波多模式频散谱成像的分辨率，本文利用改进Frequency-Bessel变换法提取主动源Love波频散曲线.该方法通过改进的0阶Frequency-Bessel变换，将多道地震记录变换到频率-波数域，获得频散能量图.通过公式推导和数值模拟，验证了该方法的有效性.实例测试表明，该方法具有较高的分辨率和多模式分辨能力，为多分量面波勘探提供了一种有效的频散分析手段.此外，本文中的实例对比分析表明，与经时间域归一化后的多道地震记录相比，Frequency-Bessel变换法可能更适合于对原始炮集记录进行频散分析.

致谢感谢两位匿名审稿专家提出的宝贵建议.