复合材料结构中螺栓拧紧的有限元仿真研究

黄稳，杜伟，凡志磊，葛恩德，安鲁陵，王楚凡

(1.中国商飞上海飞机制造有限公司，上海 201324；2.南京航空航天大学，江苏 南京210016)

0 引言

碳纤维/环氧树脂基复合材料结构在飞机设计中已经获得了大量运用，并且螺栓连接作为主要的机械连接形式，在飞机复合材料的连接中起到关键承力作用[1]。目前有限元仿真手段被广泛地应用于复合材料连接强度、疲劳方向的研究中，而相关研究表明螺栓在拧紧过程中受拧紧工艺因素影响，预紧力存在一定的偏差[2]。复合材料为各向异性材料，预紧力较大时表面容易出现应力集中现象。因此控制预紧力的数值十分重要。

当前对螺栓装配过程的有限元仿真大多忽略了螺栓的螺纹结构，以降低建模难度，减少计算量[3]。然而在螺栓拧紧过程中，螺纹结构对最终预紧力的形成至关重要，螺纹间的摩擦效应则是影响最终拧紧完成后预紧力偏差大小的主要因素之一[4]。因此针对拧紧过程的有限元仿真十分必要，需要对螺栓结构进行细致的建模，考虑螺纹结构及螺纹间摩擦效应对预紧力的影响。

本文通过24组螺栓拧紧试验获得预紧力结果，然后将有限元模型的结果与试验结果进行对照，以验证有限元计算模型的可靠性。

1 仿真方法

首先对转矩法原理进行分析，分析导致预紧力产生偏差的主要变量。目前在飞机复材结构的装配过程中，主要依赖于转矩法所建立的转矩-预紧力对应关系，即

T=KFD

(1)

式中：T为拧紧转矩；K为转矩系数；F为目标预紧力；D为螺栓的公称直径。

文献[4]认为转矩T在驱动紧固件转动拧紧时，一部分转矩需要克服紧固件支撑端面与被连接件端面的摩擦，一部分转矩需要克服螺纹之间的摩擦，剩余的转矩则为连接结构提供了预紧力，如式(2)所示。

T=Tp+Tt+Tb

(2)

式中：Tp为作用于螺纹牙的转矩；Tt为螺纹间摩擦转矩；Tb为支撑端面摩擦转矩。

在德国标准VDI 2230[5]中该公式可以具体表达为

T=F(0.16p+0.58μtd2+0.5μbdu)

(3)

式中：p为螺距；d2为螺纹中径；du为支撑端面摩擦转矩的等效直径；μt为螺纹摩擦系数；μb为支撑面摩擦系数。

在ISO 16047[6]中提出了摩擦系数的简化公式，假定螺纹摩擦系数μt与支撑面摩擦系数μb一致，用总摩擦系数μm来评估螺栓螺母在拧紧时总体的摩擦行为[2]。拧紧转矩与总摩擦系数可以表示为

T=F(0.16p+0.58μmd2+0.5μmdu)

(4)

(5)

由此可见，根本上是摩擦决定了转矩-预紧力之间的对应关系。

根据式(4)，变量T与μm共同影响了最终输出F的大小。因此后文将从T与μm两个角度，分析不同拧紧工况对T与μm的影响，从而进一步揭示拧紧工况对预紧力值的影响规律。

2 螺栓拧紧试验

2.1 试验设计

试验件如图1所示，拧紧试验平台如图2所示，组成单元测量精度如表1所示。试验对象为NAS6705与NASM1805。

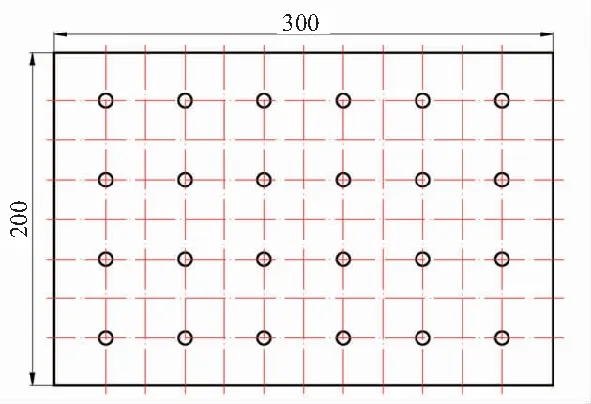
图1 200×300 mm 复材材料层压板试样

图2 立式螺栓拧紧试验平台

表1 组成单元测量精度

DOE试验设计是一门由科学试验和数据分析方法相结合的理论[7]。本文结合飞机装配现场工况选取了拧紧转速(A)、螺纹表面保持原样(B)、拧紧部位(C)、贴合面密封(D)4种工艺因素来建立试验矩阵。拧紧转速主要考虑20 r/min与200 r/min两种情况；螺纹表面考虑保持原样(Y)与经擦拭(N)两种情况；复材试样贴合面考虑涂覆密封胶(Y)与不涂覆密封胶(N)两种情况；拧紧部位考虑拧紧螺母与螺栓两种情况。

建立4因素2水平的试验矩阵，共计24组。试验的目标拧紧转矩为18.6 N·m，拧紧后的预紧力结果如表2所示。

表2 拧紧试验与有限元仿真结果对比

为了避免实验中自锁螺母拧紧过程产生的自锁转矩Tlock对转矩法计算结果的影响，使用式(6)进行处理[8]，Tr为参与计算的转矩。

Tr=T-Tlock=KFD

(6)

2.2 预紧力的偏差情况

根据试验结果，在18.6 N·m目标转矩下，预紧力的范围为[11 032 N，23 820.8 N]。在设计试验矩阵时，4、5、14组为正常拧紧工况。因此将4、5、14试验组视为正常拧紧工况下3组重复试验，测得其平均预紧力F为15 281.3 N。

由于拧紧试验是基于转矩法，因此直接将15 281.3 N近似为目标预紧力。试验中的最大预紧力为23 820.8 N，相比目标预紧力存在55.8%的偏差。

3 拧紧过程的有限元仿真

3.1 参数化紧固件模型的建立

在以往一些带螺纹升角的螺栓有限元模型中，通常采用Hypemesh软件来进行网格的划分。由于螺纹紧固件中螺纹升角的存在，导致螺纹有限元模型较为复杂，网格划分较为困难，且多为C3D4四面体网格[4]。C3D4型的线性四面体网格计算精度不高，并不适用于模拟螺栓拧紧的过程以及预紧力的计算，相对而言C3D8型的六面体网格计算精度更高，且结构较为简单，应当尽量通过六面体网格对螺纹结构进行划分。

本文参考FUKUOKA T的螺纹六面体网格划分方法[9]，进行简化处理，实现了对螺纹紧固件的参数化建模。首先根据机械设计中对于螺纹轮廓的定义，计算出螺纹外轮廓的节点坐标，如图3(a)所示；然后按比例将轮廓节点坐标向轴心缩小，如图3(b)所示；根据角度与螺纹节距的关系将截面进行旋转堆叠，然后按C3D8网格的节点排布方式为节点编号排序，获得一层C3D8网格模型，如图3(c)所示；将该层网格模型按照角度与螺纹节距关系继续旋转堆叠，获得一个节距内的螺纹模型，如图3(d)所示；将一个螺距内的螺纹进行多次复制，便可以获得整段螺纹结构模型，螺母处内螺纹同理，最终模型如图4所示。

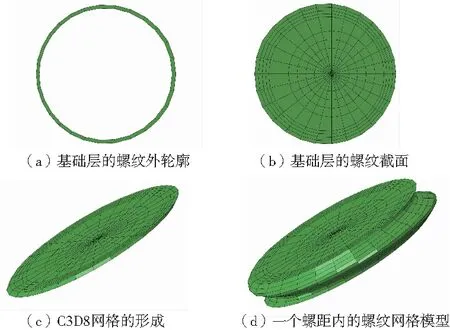
图3 螺纹网格模型建立的过程

图4 螺栓螺母有限元网格模型

3.2 接触属性与边界条件设置

从计算精度以及节约计算资源的角度考虑，法向接触算法选择增广拉格朗日法，切向的接触算法选择罚函数。对于接触面间的相对运动，在螺纹间与端面间需要采用有限滑移公式来描述接触面之间发生的大位移。而其余接触面之间在拧紧过程中基本不会发生较大的相对位移，相对滑动很小，从节省计算代价的角度考虑在其余接触中选用小滑移公式进行设置。基于前文中对于总摩擦系数μm的假设，螺纹间摩擦系数与端面的摩擦系数相等，由此将μm的值分别带入二者的切向罚函数设置中，其余接触面的摩擦系数均设置为0.1[10]，总体接触设置如图5所示。

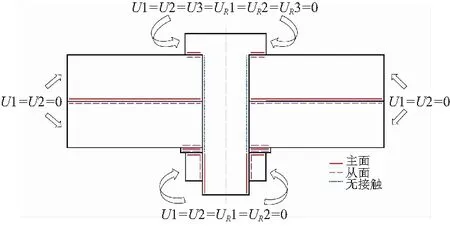
图5 连接件接触关系与边界条件设定示意图

为了模拟连接结构的实际拧紧过程，对于复合材料试样约束其在水平面内U1与U2向的自由度防止拧紧过程中旋转。对于螺栓螺母，旋转端在拧紧过程中会有轴向的移动，约束其在U1、U2、UR1与UR2的自由度，通过UR3方向施加拧紧转矩进行拧紧；非旋转端在拧紧过程中几乎不产生运动，约束其6个方向的自由度。对于垫圈，不考虑其与复合材料之间的相对旋转运动，因此约束其在U1、U2、UR3上的自由度。

3.3 计算结果对比

为了验证通过转矩与摩擦系数两个参量在有限元中模拟拧紧工艺因素对预紧力影响的可行性，在有限元中对24组拧紧试验依次进行仿真。根据表2中试验处理获得的数据，将有效转矩Tr、总摩擦系数μm作为有限元计算的输入参量，同时还需考虑拧紧时紧固件的尺寸结构影响，将拧紧部位作为边界条件变量一并纳入考量。24组仿真结果与试验结果对比如表2所示。

以预紧力的试验结果作为基准，计算仿真获得的预紧力误差。对比可以发现仿真获得的预紧力误差整体都控制在4%以内，当计算转矩Tr=14.1 N·m、总摩擦系数μm=0.090时，仿真误差最小为0.42%；当计算转矩Tr=15.1 N·m、总摩擦系数μm=0.055时，仿真误差最大为3.96%。由此可说明有限元模型总体可靠。

3.4 复材表面应力分析

对预紧力偏差最大的情况，即试验17中预紧力为23 820.8 N、有限元仿真中预紧力为23 138.3 N的情况展开分析，与试验结果相比有限元计算结果存在2.87%的误差。

对螺母端复材表面与螺栓头端复材表面的平面应力情况进行分析。沿复材板的孔边径向提取5段圆周路径上的64处节点的应力值，绘制角度-应力曲线。将螺母端复材板的孔边曲线即距孔圆心半径为3.97 mm、5.485 mm、7.00 mm、8.5 mm、10 mm的圆周路径分别记为Nut-1、Nut-2、Nut-3、Nut-4、Nut-5，螺栓端同理，如图6所示，并以虚线为起始顺时针提取应力值。为了更加直观地对比拧紧时复材表面不同区域的应力变化趋势，将复材局部直角坐标系下的σx、σy、τxy应力分量转化到极坐标系之下，得到径向应力分量σr、周向应力分量σθ、径向与轴向的切向应力分量τrθ，具体转化公式如下：

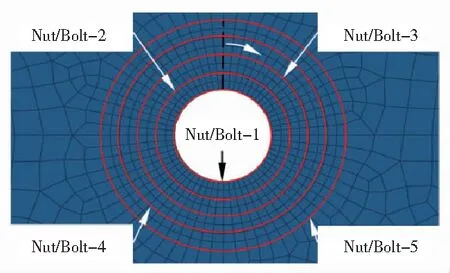
图6 复材表面应力提取路径

(7)

(8)

(9)

对于螺栓头端复材的表面径向应力σr，如图7(a)中1、2处的圆周路径整体为负值，呈受压状态；1处圆周路径的压应力峰值为488.26 MPa，要大于2处的圆周路径的压应力峰值457.21 MPa。3、4、5处的圆周路径整体为正值，呈受拉状态，3处的圆周路径拉应力峰值为326.16 MPa，大于4、5处的圆周路径拉应力峰值266.13 MPa与169.84 MPa。

对于螺栓头端复材的表面周向应力σθ，如图7(c)所示，其压应力与拉应力的分界情况与径向应力σr基本一致。1处圆周路径的压应力峰值为477.65 MPa，要大于2处的圆周路径的压应力峰值447.09 MPa，压应力峰值出现的角度并不一致；3处的圆周路径拉应力峰值为346.99 MPa大于4、5处的圆周路径拉应力峰值285.79 MPa与188.25 MPa。

对于螺母端复材表面的径向应力σr，如图7(b)中1、2处的圆周路径整体为负值，主要呈受压状态；4、5处的圆周路径整体为正值，呈受拉状态。相比螺栓端复材表面的径向应力：整体应力水平出现了显著降低；3处圆周路径的应力曲线整体处于0刻度线附近；孔边1处圆周路径的压应力水平相比2处整体所有降低。螺母端1、2处的径向压应力峰值相比螺栓端分别下降了57.1%与41.1%；3、4、5处的径向拉应力峰值相比螺栓端分别下降了92.8%、46.4%与49.5%。

对于螺母端复材表面的周向应力σθ，如图7(d)所示，其压应力与拉应力的分布情况与径向应力σr基本一致。螺母端1、2处的周向压应力峰值相比螺栓端分别下降了53.1%与53.2%；3、4、5处的周向拉应力峰值相比螺栓端分别下降了85.0%、41.5%与43.5%。

图7 复材板孔周圆周路径上的径向与周向应力

根据上述分析可以发现，从径向上看半径为3.97 mm到10 mm的圆周路径中，复材板表面应力变化趋势并不一致。总体来看，由于复材板孔周受到紧固件端面的挤压而易产生下陷趋势，从而造成螺栓头凸台对复材压痕以外的圆周路径4、5整体呈受拉趋势；而靠近孔边区域的圆周路径1、2上由于受到孔边外形的约束，材料在下陷过程中易呈现堆积状态，从而造成整体呈受压的趋势。对比螺栓头端与螺母端的平面应力情况，螺母端垫圈的存在极大程度上减弱了圆周路径3上的拉应力峰值，并改善了复材表面整体的应力水平，减缓了应力集中的趋势。

4 结语

1)从理论角度进行分析，说明拧紧转矩与摩擦系数是影响转矩法拧紧后预紧力大小的主要参数。将拧紧转矩与摩擦系数作为变量输至有限元模型中，以此模拟螺栓的拧紧过程，计算预紧力的大小。

2)精简了FUKUOKA T所提出的螺纹六面体网格划分方法，将有限元计算得到的预紧力与试验所获得的预紧力比较，该有限元模型的计算误差在4%以内。

3)分析了复合材料表面的应力分布情况，复材表面的应力分布情况较为复杂，从极坐标的角度看孔周平面的应力情况，可以将其看作由拉伸区域与压缩区域两块组成，可能诱发损伤的产生。此外，垫圈有改善复材表面应力集中的作用。