基于SDP与CNN的石油钻探用柱塞泵斜盘不平衡故障诊断

王建强

(中国石油大学(华东)石油工业训练中心，山东 青岛 266580)

0 引言

目前，柱塞泵已成为石油钻探行业的一个重要设备，该设备的运行控制性能对石油钻探过程的可靠性存在直接影响。柱塞泵具有结构紧凑、寿命长、容积效率高等优点[1-3]。柱塞泵的典型故障包括滑靴磨损、松靴、配流盘磨损以及斜盘不平衡。由于柱塞泵的故障具有突发性，成因复杂，使用提取特征与分类器结合的传统方法对柱塞泵的故障诊断变得十分困难，尤其是斜盘不平衡故障更不易发现。对柱塞泵初期故障如何实现快速预警以及准确判断故障信号，这是避免因故障问题造成经济损失的重要问题[4-6]。

深度学习与机器学习算法已被应用于故障诊断领域[7-8]。可通过深度学习提取得到特征信息，根据故障数据完成深度学习过程并实现故障的诊断功能。相对传统形式的机器学习算法，可以采用深度学习网络实现学习与识别过程的高效结合，由此满足特征参数提取、训练以及对准确率进行控制的要求，显著提升模型诊断能力[9-11]。进行信号处理时，可以利用对称点模式(symmetrized dot patterns, SDP)图像显示模式使不同信号间的差异性表示成图像形式，再对转换得到的图像进行深度学习，由此达到自适应提取SDP图像信息的效果，克服人工特征提取方式存在的缺陷[12-13]。

斜盘时域信号内存在振动信号的各项特征数据，当直接对这些数据开展深度学习时并不能获得理想的识别精度。为优化深度学习模型诊断性能，本文构建了以SDP图像和卷积神经网络(convolutional neual networks, CNN)相结合的方式来实现斜盘的故障诊断功能。利用SDP方法分析故障信号，对包含故障信息的时域信号进行转换得到SDP图像，根据图像差异性判断不同的故障类型；再把SDP图像参数输入CNN中进行处理，由此完成识别SDP图像的功能，从而判断出故障类型。

1 SDP信号分析方法

1.1 SDP图像概述

采用SDP模式进行图像处理是把信号转换成图像的过程。与其他信号图形转换方法相比，该方法转化计算过程较简单。可以把时域信号以SDP图像形式表示，不必对信号实施滤波与降噪，采集得到信号中的有用信息[14]。

对时域信号进行归一化，得到对应极坐标系的SDP图像，将其表示成式(1)的形式。

(1)

式中：i是采样过程中时域信号包含第i个离散点，用SDP计算时间点i的幅值xi和时间点i+a的幅值xi+a，并把结果转换成极坐标的形式，根据时域信号的xi参数转化得到SDP图像的半径尺寸；θl是极坐标系初始角度；xmax与xmin依次表示时域信号xi的最大与最小值。可以把时间滞后系数a以及时域信号各点都映射到极坐标系内。

SDP方法可以利用极坐标系表示时域信号，得到具有信号变化特征的图像。与其他时域信号转化成图像的方式相比，采用SDP图像可以获得更优抗噪声性能。

1.2 仿真信号及SDP图像表达

利用SDP图像表示信号时，能够同时表达不同组的信号。本文对包含不同频率的故障信号进行模拟测试，同时对比了各频率信号被转换成SDP图像时的差别，对各位置处形成的模拟信号分析，重点探讨了图像和信号频率的相互变化规律[15]。

测试时，总共设置了4种频率成分的正弦信号，将其转换成SDP图像的形式，可以同步把多组信号转化成SDP图像。图1为仿真信号波形图。

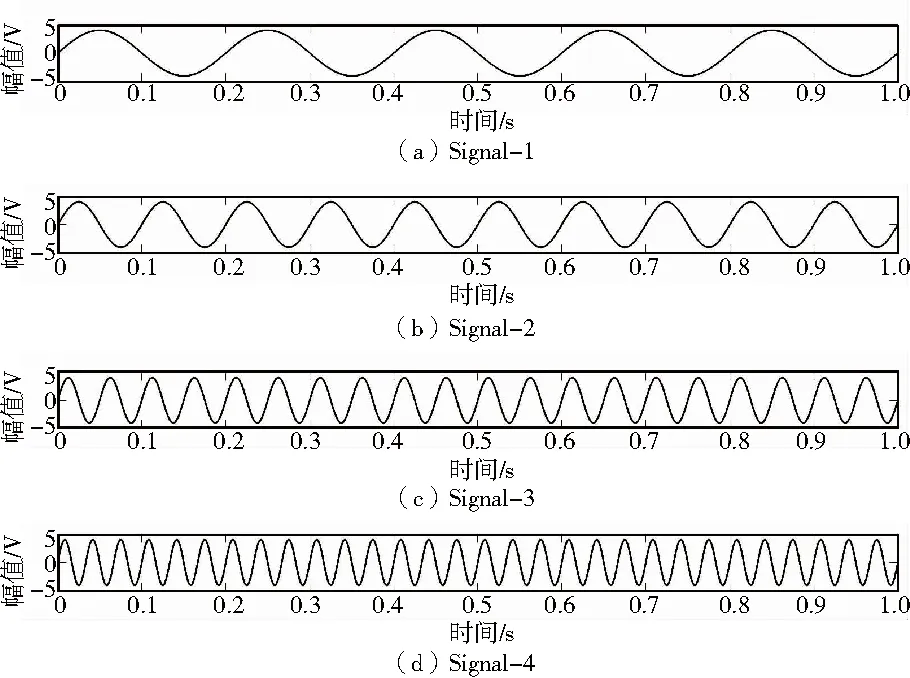
图1 仿真信号波形图

当逐渐提高频率成分时，各组信号被转化成SDP图像之后，对应的图像曲率也存在明显区别，由此可以推断将信号转化成SDP图像时实际可表达信号也具有较大差异性。

2 故障诊断方案

2.1 信号采集

机械故障综合模拟测试台是SQI企业设计的一种测试台，实验装置见图2。组成信号采集系统的部分包含加速度探测器、计算机与DEWE信号采集仪。

图2 实验装置图

斜盘不平衡即斜盘中心与轴中心不重合，在斜盘运转过程中会出现较大径向冲击，原理示意及模拟照片见图3。在添加不平衡螺钉后，在转盘上形成不平衡区域。

图3 斜盘不平衡故障原理及模拟照片

进行斜盘不平衡故障模拟时，控制测试台转速为600 r/min，以1 260 Hz频率进行采样。各类故障分别采集得到500个样本，从中选择400组进行训练，再以剩余100组作为测试对象，各组数据分别采样1 024点，本次故障测试共包含2 000个数据。

2.2 基于SDP图像与CNN的斜盘故障程度诊断

利用深度学习CNN提取故障信号SDP图像特征并完成学习过程，根据SDP图像类型判别结果来达到分辨振动状态的效果。图4给出了本文设计的故障诊断流程。

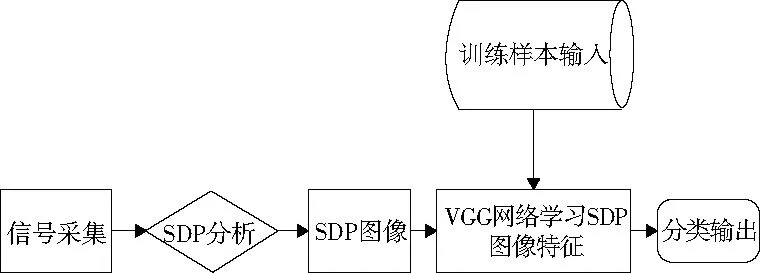
图4 基于SDP图像和CNN的故障诊断流程

构建卷积神经网络CNN模型后，再对故障信号转化得到的SDP图像实施分类，当设置不同的神经网络参数时，诊断模型识别精度也会发生明显变化。对故障信号进行SDP分析，通过信息融合的方法将其转化成图像，再把转化得到的图像输入CNN诊断模型。

3 CNN结构参数优化

分别设置了1 600个训练数据域400个测试数据，设定输入图像的像素为128×128。对各训练样本开展一次训练后得到对应的迭代次数，根据模型结构测试时，结合实际经验控制训练次数为20次，将尺寸设定在32，第一卷积层中总共包含32个卷积核，网络学习率为0.1。

3.1 网络结构

CNN-16网络包含了5层卷积层与池化层，可以通过对网络进行加深处理来提升运算性能。各网络结构故障的识别准确率结果见图5。根据图5可知，故障识别结果受到实际网络结构的直接影响。对各网络结构测试后，再结合故障识别与网络训练效率的情况，利用4层卷积层网络构建故障诊断模型。

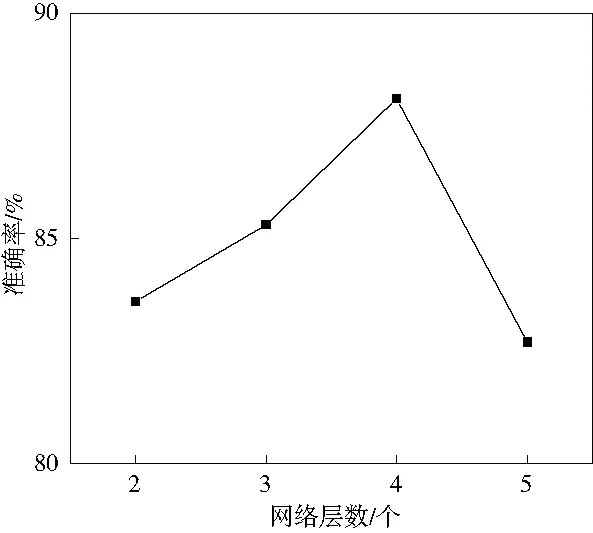
图5 不同网络结构的故障诊断结果

3.2 尺寸batchsize对识别准确率的影响

图6显示了在不同尺寸下进行故障识别得到的准确率。根据图6可知，尺寸从8提高至32时，模型识别准确率随尺寸表现为快速升高的趋势。尺寸为32的条件下，此模型可以达到88.1%的最高准确率。进行本次测试时，尺寸为32时达到了最高识别准确率，根据时间损耗以32作为最终尺寸。

图6 识别准确率随尺寸的变化曲线

3.3 卷积核个数

图7显示了识别准确率随第一层卷积核数量变化结果。根据图7可知，当第一层的卷积核数为8、16、32与64时，通过模型计算得到的识别准确率存在差异性。根据模型训练时间、稳定性及其在故障识别方面的准确率，以第一层卷积核数量32作为深度学习模型卷积层。

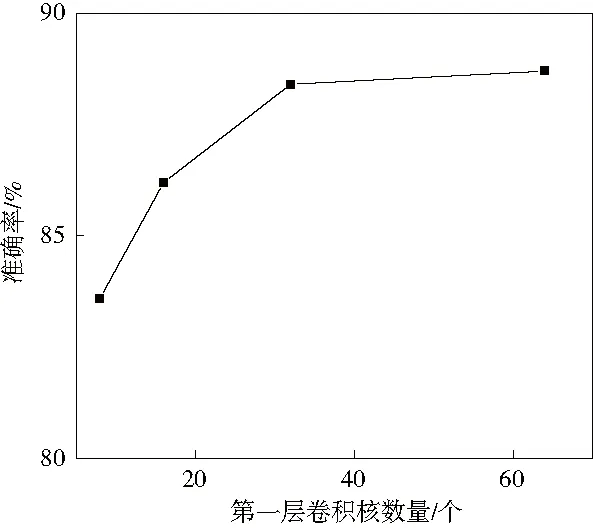
图7 识别准确率随第一层卷积核数量的变化

3.4 网络中学习率

图8显示了识别准确率随深度模型学习率的变化结果。根据图8曲线可知，识别准确率随学习率的增加表现出先增加后减小的变化规律，在学习率为0.1时达到最大值。因此确定深度学习以学习率0.1为参数。

图8 识别准确率随深度模型学习率的变化趋势

4 训练结果分析

以尺寸batchsize32、迭代次数为20、学习率为0.1并且第一层卷积核数32的参数作为模型参数；以随机方式从故障数据库内选出100组样本进行测试，总共为400组。再以剩余1 600组数据对模型进行训练。CNN也对计算结果存在显著影响，通过比较各参数可知，设定CNN学习率为0.1，每次输入32个样本进行训练，总共迭代20次，其中，在第一卷积层内包含的卷积核数量为32，同时输入像素为128×128的图像。表1是对不同故障程度转子进行识别的结果。

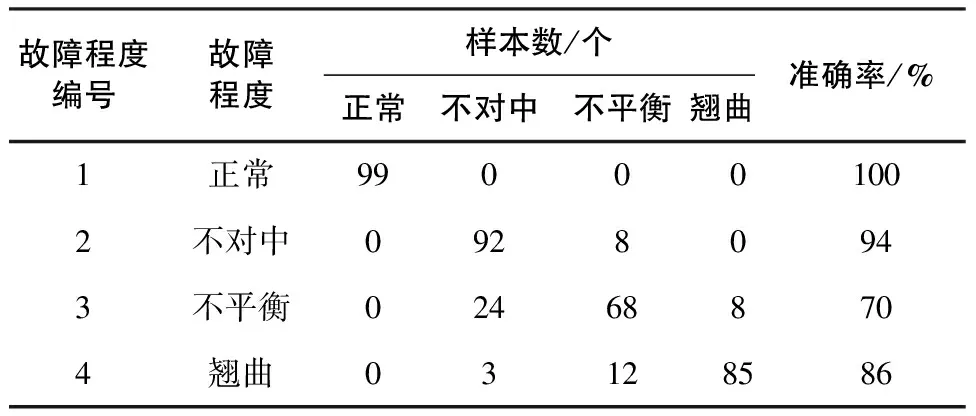
表1 不同故障程度转子识别准确率

在上述参数下，以模型对故障进行识别得到的4种故障准确率均值为87.4%，故障程度3达到了最小的准确率。这是因为：相比较不对中和翘曲故障，转子高速运转时不平衡故障会引起高频振动，致使发生失稳的概率增加。

为了进一步证明，采用频域分析对振动信号进行谱图分析，加速度传感器振动信号耦合故障频域谱图见图9。

图9 耦合故障频域谱图

分析图9可知，频域谱图信号表现为不平衡特点，在轴向方向表现为不对中的故障特性。通过对时域信号特征提取可有效地提高耦合故障类别的判断准确率。

5 结语

1)以尺寸batchsize32、卷积层为4、学习率为0.1并且第一层卷积核数32的参数作为模型参数是最优的。

2)控制输入图片尺寸为128×128的条件下，模型识别的准确率为87.4%，由此达到对各程度故障进行分类的效果。通过对时域信号特征提取可有效地提高耦合故障类别的判断准确率。