基于速度空间非结构网格和守恒修正的改进离散速度方法
2023-01-10杨鲤铭吴杰董昊杜银杰
杨鲤铭,吴杰,董昊,杜银杰
南京航空航天大学 航空学院,南京 210016
跨流域流动问题广泛存在于工程实际中,譬如微电子机械系统[1-2]和载入飞行器[3-5]。对于该类问题,由于分子平均自由程非常接近或远大于几何的特征尺度,连续性假设不再成立,因而Navier-Stokes方程不再适用。相比于Navier-Stokes方程,Boltzmann方程直接描述气体分子的分布函数,没有引入连续性假设,因而理论上可用于从连续到自由分子流整个流域范围。为了求解Boltzmann方程,离散速度方法(Discrete Velocity Method,DVM)经常被采用[6-7],该方法在物理空间和分子速度空间同时离散求解Boltzmann方程。
基于不同的通量重构方式和分布函数演化策略,文献中提出了多种算法。其中,借鉴传统计算流体力学中求解Navier-Stokes方程的通量重构方法,即不考虑分子碰撞效应的迎风格式被广泛用于重构Boltzmann-BGK方程的通量。例如,Yang和Huang[8]、Mieussens[9]采用了二阶迎风格式,Wang等[10]采用了三阶迎风格式,Kudryavtsev和Shershnev[11]、Diaz等[12]采用了WENO格式。由于通量计算时不考虑分子碰撞的影响,因而无需联立所有的离散分布函数来计算单元界面的平衡态,所以该方法非常简单,且易于在离散速度空间并行化计算。然而该方法在连续和近连续流区域也会导致一些问题,主要原因在于这些区域的分子平均自由程非常小,而物理空间的网格尺度很难小于分子平均自由程,所以分子的碰撞对通量计算的贡献不可忽略。不考虑分子碰撞的影响时,会使得连续和近连续流区域计算的结果不准确。另一方面,由于最新时刻的平衡态是未知的,Boltzmann-BGK方程的碰撞项一般只能采用半隐式来离散,会导致连续和近连续流区域计算收敛速度较慢[13-14]。
为了克服上述传统DVM的缺陷,一些新的算法被提出用于求解Boltzmann-BGK方程。譬如,气体动理学统一算法(Gas Kinetic Unified Algorithm,GKUA)[15-17]、统一气体动理学格式(Unified Gas Kinetic Scheme,UGKS)[18-20]、离散统一气体动理学格式(Discrete Unified Gas Kinetic Scheme,DUGKS)[21-22]等。其中UGKS在计算通量时采用了含碰撞项Boltzmann-BGK方程的局部积分解,同时同步求解了与Boltzmann-BGK方程对应的宏观伴随方程。由于通量重构考虑了分子碰撞的影响,UGKS在连续和近连续流区域也可以获得准确可靠的结果。另外,由于同步求解了宏观伴随方程,其预估的平衡态可用于实现Boltzmann-BGK方程碰撞项的全隐式离散,从而极大地提高了连续流区域的收敛速度。但是,含碰撞项Boltzmann-BGK方程的局部积分解较为复杂,UGKS在过渡流和自由分子流区域的计算效率通常低于传统DVM。此外,UGKS需要联立所有的离散分布函数来计算单元界面的宏观量,进而计算平衡态分布。
最近,为了保持传统DVM的简单性优势,同时克服其在连续流和近连续流区域计算精度差、计算效率低的缺陷,Yang等[23-24]提出了一种改进离散速度方法(Improved Discrete Velocity Method,IDVM)。IDVM的设计思想是基于传统DVM在过渡流和自由分子流区域可以获得可靠的计算结果,而在连续和近连续流区域精度差、效率低的表现,通过引入宏观伴随方程来完善其在全流域的计算性能。与UGKS类似,该方法也同步求解了Boltzmann-BGK方程和相应的宏观伴随方程,且在计算宏观伴随方程通量时考虑了分子碰撞的影响,可以视为UGKS的同类算法。但不同于UGKS,IDVM在求解Boltzmann-BGK方程时,单元界面通量的计算没有耦合碰撞项,保持与传统DVM一致。没有耦合碰撞项的原因在于传统DVM在过渡流和自由分子流区域可以获得可靠的解,而在连续和近连续流区域,宏观伴随方程将主导流场解,此时由于该方程通量的计算耦合了碰撞项,亦可获得合理的解。通过这种策略,既不会破坏传统DVM的简单性优势,同时还保证了全流域的计算精度。此外,由于同步求解了相应的宏观伴随方程,可以利用预估的平衡态来实现Boltzmann-BGK方程碰撞项的全隐式离散,从而提高算法在连续流区域的收敛速度。实际上,在传统DVM基础上,通过引入宏观伴随方程来提高连续和近连续流区域的计算精度和计算效率的思想在Chen[25]和皮兴才[26]等的工作中也已经被应用和验证。但是,由于宏观伴随方程的通量和Boltzmann-BGK方程的通量计算不一致,该类方法在理论上存在不自洽的问题,需要在后续工作中进一步完善。
为了进一步提高IDVM的计算效率,本文将着重研究不同速度空间求积方式和守恒修正对结果的影响,实现速度空间网格量的尽可能降低。在IDVM中,宏观物理量由离散分布函数求积而得到,其实质为对基于离散点所构造的多项式进行积分,因而会受到多项式误差的影响。使用均匀节点构造高次多项式时,区间边缘的误差可能很大,从而导致Runge现象[27]。这意味着,高阶的求积格式并不一定总能获得高精度的结果。所以,在克努森数(Kn)较大的情形,由于分布函数严重偏离平衡态,矩形求积规则反而更容易保证结果的可靠性;而在宏观速度较低和Kn数较小的情形,由于分布函数接近平衡态且关于原点基本对称,可以采用Gauss-Hermite积分来获得高精度结果。此外,由于分布函数仅在宏观速度附近时值较大,而远离该区域的值逐渐变小,所以采用非结构网格来离散速度空间更能充分利用分布函数的这一特征,实现速度空间网格量的降低。最后,由于数值积分获得的宏观量与真实积分结果存在误差,可能会导致相容性条件不能严格满足,使得误差累积或计算发散。为了克服这一问题,本文还引进了守恒修正来强制满足相容性条件,使得较粗糙的速度空间网格也可以获得准确的计算结果,从而进一步提升计算效率。
1 Boltzmann方程和传统离散速度方法
原始的Boltzmann方程是积分-微分形式,求解较为困难。针对航天领域所关注的气动力和气动热问题,可以求解采用BGK-Shakhov模型[28]来近似碰撞项的Boltzmann-BGK方程
(1)
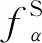
(2)
(3)
式中:Pr为普朗特数;c=ξ-u为分子的特异速度,u为宏观速度;q为热流;ρ为密度;T为温度;Rg为气体常数。另外,文中约定用黑体来表示矢量,用对应的白斜体来表示矢量的模。
离散分布函数fα与宏观守恒量W、宏观通量F、热流q和应力τ存在如下关系:
W=[ρρuρE]T=〈ψf〉α
(4)
F=[FρFρuFρE]T=〈ξψf〉α
(5)
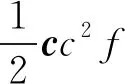
(6)
τ=〈ccf〉α
(7)

(8)
式中:上标n表示当前时刻;Δt代表隐式推进的时间步长,由如下CFL条件确定:
Δt=

(9)
式中:σ为CFL数;V为控制体的体积;ξ1,max、ξ2,max和ξ3,max分别为x、y和z这3个方向的最大离散速度;ΔSx、ΔSy和ΔSz为控制体在y-z平面、x-z平面和x-y平面的投影面积;cs为声速。
(10)
对方程(10)在控制体Vi积分可得
(11)
(12)
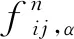
(13)
(14)
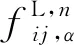
(15)
式中:H(nij·ξα)为台阶函数,当nij·ξα≥0时有H(nij·ξα)=1,而当nij·ξα<0时有H(nij·ξα)=0。
(16)
(17)
(18)
自此,方程(16)可以采用高效的LU-SGS方法来求解,分为如下的前扫和后扫两步:
(19)
(20)
式中:L(i)和U(i)为N(i)的子集,分别包含单元编号大于i和小于i的单元。
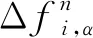
2 改进离散速度方法
2.1 Boltzmann-BGK方程求解
为了克服传统半隐式DVM在连续和近连续流区域收敛速度较慢的缺陷,IDVM采用了全隐式方法来离散Boltzmann-BGK方程
(21)

(22)
(23)
(24)

2.2 宏观伴随方程求解
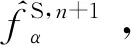
(25)
(26)

(27)
式中:C(i)为包含i单元和其周围单元的集合。将方程(27)代入方程(26)可得:
(28)
在应用LU-SGS求解方程(28)时,为了避免矩阵运算,可采用基于Euler方程的通量分裂算法来近似雅克比矩阵∂R/∂W,即
(29)
将方程(29)代入方程(28)可得:
(30)
式中:
(31)
Fc=[ρuρuu+pI(ρE+p)u]T
(32)
(33)
自此,方程(30)可以通过如下的前扫和后扫求解:
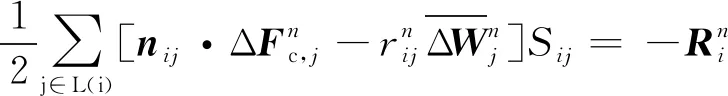
(34)
(35)


(36)
式中:fcol(xij,ξ,Δtp)为单元界面考虑了分子碰撞影响的Boltzmann-BGK方程的局部解,Δtp为通量重构的时间步长,其可以通过方程(9)计算,但CFL数需要设置为小于1,本文选取0.95。通过相关推导发现[14],fcol(xij,ξ,Δtp)最终可以表示为
fcol(xij,ξ,Δtp)=βfDVM(xij,ξα,Δtp)+
(1-β)fNS(xij,ξα,Δtp)
(37)
β=e-Δtp/τ
(38)
式中:fDVM(xij,ξα,Δtp)为无碰撞Boltzmann方程在单元界面的局部解,即方程(15)。fNS(xij,ξα,Δtp)为对应于连续流极限的分布函数。将方程(37)代入方程(36)有
〈ξψfNS(xij,ξ,Δtp)〉α=
(39)
式中:右端第1项可以通过将方程(15)代入进行计算,第2项实际上是Navier-Stokes方程的通量,可以采用常用的连续流求解器进行计算。采用Yang等[29]提出的LBFS算法进行求解。
2.3 速度空间离散与求解规则
在DVM中,由于速度空间被离散化,必须通过数值积分来计算宏观量以及平衡态分布函数。因而,速度空间的离散化策略和求积规则的选取对计算精度和效率将产生直接的影响。对于低速且接近平衡态的流动,由于分布函数基本上呈正态分布,可以采用精度较高的Gauss-Hermite积分。以φ(ξ)在一维速度空间的积分为例
(40)
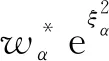
(41)
式中:HNV-1为NV-1阶Hermite多项式。
对于高速流动和远离平衡态的流动问题,由于分布函数可能会出现“双峰”等不规则分布,一般可采用复化Newton-Cotes积分
(42)
目前文献中应用较多的是四阶Newton-Cotes公式,但高阶积分可能会出现Runge现象。本文将比较一阶到四阶Newton-Cotes公式的计算效果。
实际上,当采用一阶Newton-Cotes公式时,可以用非结构网格来离散速度空间。此时的求积点即为控制体的中心点,求积权即为控制体的体积。采用非结构网格来离散速度空间的另一个优势是可以仅在分布函数值可能较大的区域布置密网格,而在其他区域采用粗网格,以减少总的速度空间网格量。非结构网格速度空间离散已在Yuan和Zhong[30]和Chen等[31]的工作中被应用。由于无法预知分布函数在速度空间中的准确分布,采用非结构网格来离散速度空间时需要人为选择截断区域和加密区域。文中截断区域取为
(43)
加密区域取为
(44)
式中:Ts为总温;u0为流场中的最大和最小速度的均值。它们可以通过Navier-Stokes方程解来预估;系数a取值为4~5之间。
2.4 相容性条件与守恒修正
由于DVM中采用数值积分来计算宏观量,相容性条件将不能严格满足,从而可能会导致误差累积或计算发散。为了解决这一问题,需要强制满足相容性条件[32-33],即
〈ψ1(fS-f)〉α=[000 -Prq]T
(45)
式中:ψ1=[1ξξ2/2cc2/2]T。由于fS是宏观量的函数,而f在当前时刻是常数,方程(45)实际上是变量ћ=[ρuTq]T的非线性多元函数。为了便于求解,可以引进如下辅助函数:
Φ(ћ)=〈ψ1(fS-f)〉α-
[000 -Prq]T=0
(46)
方程(46)可以采用牛顿迭代求解
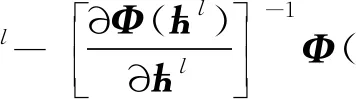
(47)
实际计算时,可以将ћ1取为f求矩的结果。该算法收敛非常快,一般迭代2~4步残差就可以收敛到10-9。
3 算例测试与验证
本节通过几个低速到超声速、连续到自由分子流算例来检验当前算法的精度和效率。由于所考虑的算例均为定常流动,为了加速计算,宏观伴随方程求解时采用了50次内迭代,以此来获得更为准确的预估平衡态。此外,本文所有算例均只考虑单原子分子情形,对应的比热比为5/3。所有计算均在个人计算机上完成,其配置为Intel(R) Xeon(R) Gold 6226R CPU@2.90 GHz。
3.1 顶盖驱动流
顶盖驱动流为经典测试算例,可以通过调节Kn数或Re数来实现流动从连续流变为自由分子流状态。该算例中,顶盖的无量纲温度和速度分别为TW=1和uW=0.15,其他壁面保持静止且温度固定为TW=1。无量纲动力学黏性系数计算如下:
μ=μrefTw
(48)
该算例采用变径硬球模型,取w=0.81。另外,对于给定Kn数或Re数的情形,分别采用方程(49)或方程(50)来计算参考黏性系数μref
(49)
(50)
式中:ρ0=1和T0=TW分别为参考的无量纲密度和温度。计算时,采用相邻两步原始变量的1-范数误差最大值小于10-7作为收敛判据。
首先,以Kn=10的算例来测试不同阶数的Newton-Cotes积分对计算结果的影响。计算时,将速度空间截断为[-4, 4]×[-4, 4],并用24×24的均匀结构网格对其进行离散。计算得到的中截面速度分布如图1所示。可以看出,当速度空间网格非常稀疏时,较小阶数的Newton-Cotes积分(n=1)的结果反而优于高阶Newton-Cotes积分(n=4)。由此表明,高Kn数时,高阶Newton-Cotes积分可能会导致Runge现象。所以在后续计算中,如果Kn数较大或者流动速度较高时,均采用一阶Newton-Cotes积分(即矩形律),并利用非结构网格来离散速度空间。

图1 采用不同阶数Newton-Cotes积分获得的速度分布比较
其次,验证当前算法在全流域计算时的精度。测试状态包含Re=100,1 000的连续流,Kn=0.075的滑移流,Kn=1的过渡流和Kn=10的自由分子流。连续流和滑移流计算时分别采用8×8和28×28个离散点的Gauss-Hermite积分,而过渡流和自由分子流采用包含1 648个三角形单元的非结构网格对速度空间进行离散,如图2所示。另外,连续流计算时采用包含10 000个四边形单元的均匀非结构网格对物理空间进行离散,而其他工况则采用包含1 600个四边形单元的均匀非结构网格。图3展示了Re=1 000,Kn=0.075和Kn=10时,采用IDVM计算的结果。可以看出,无论在连续流区域(Ghia等的结果[34])还是稀薄流区域(DSMC的计算结果[35]),IDVM都可以获得准确合理的结果。Re=100和Kn=1的计算结果也与参考解吻合,但限于篇幅,图中未展示。
最后,验证速度空间非结构网格和守恒修正对IDVM计算效率和内存开销的影响,同时比较IDVM和UGKS的性能。顶盖驱动流问题中,原始IDVM仅在Kn=1的过渡流和Kn=10的自由分子流计算时需要采用Newton-Cotes积分,因此选用这两个工况来比较不同算法的性能。为了获得光滑的流场分布,原始IDVM一般需要采用101×101的均匀结构网格来对速度空间进行离散。而采用非结构网格离散速度空间时仅需要1 648个网格单元,内存开销约为原始IDVM的16%。
图4比较了采用和不采用非结构网格速度空间和守恒修正IDVM以及采用非结构网格速度空间UGKS计算得到的温度云图。图中云图背景和黑线为UGKS的计算结果,红线和白线分别为采用和不采用非结构网格速度空间和守恒修正IDVM的计算结果。可以看出3种格式计算的结果基本一致。另外,表1比较了采用和不采用非结构网格速度空间和守恒修正IDVM的迭代次数和计算时间。显然,引入非结构网格速度空间和守恒修正后,计算效率得到了明显提升。

图2 顶盖驱动流问题的速度空间非结构网格

图3 采用IDVM计算的顶盖驱动流速度分布
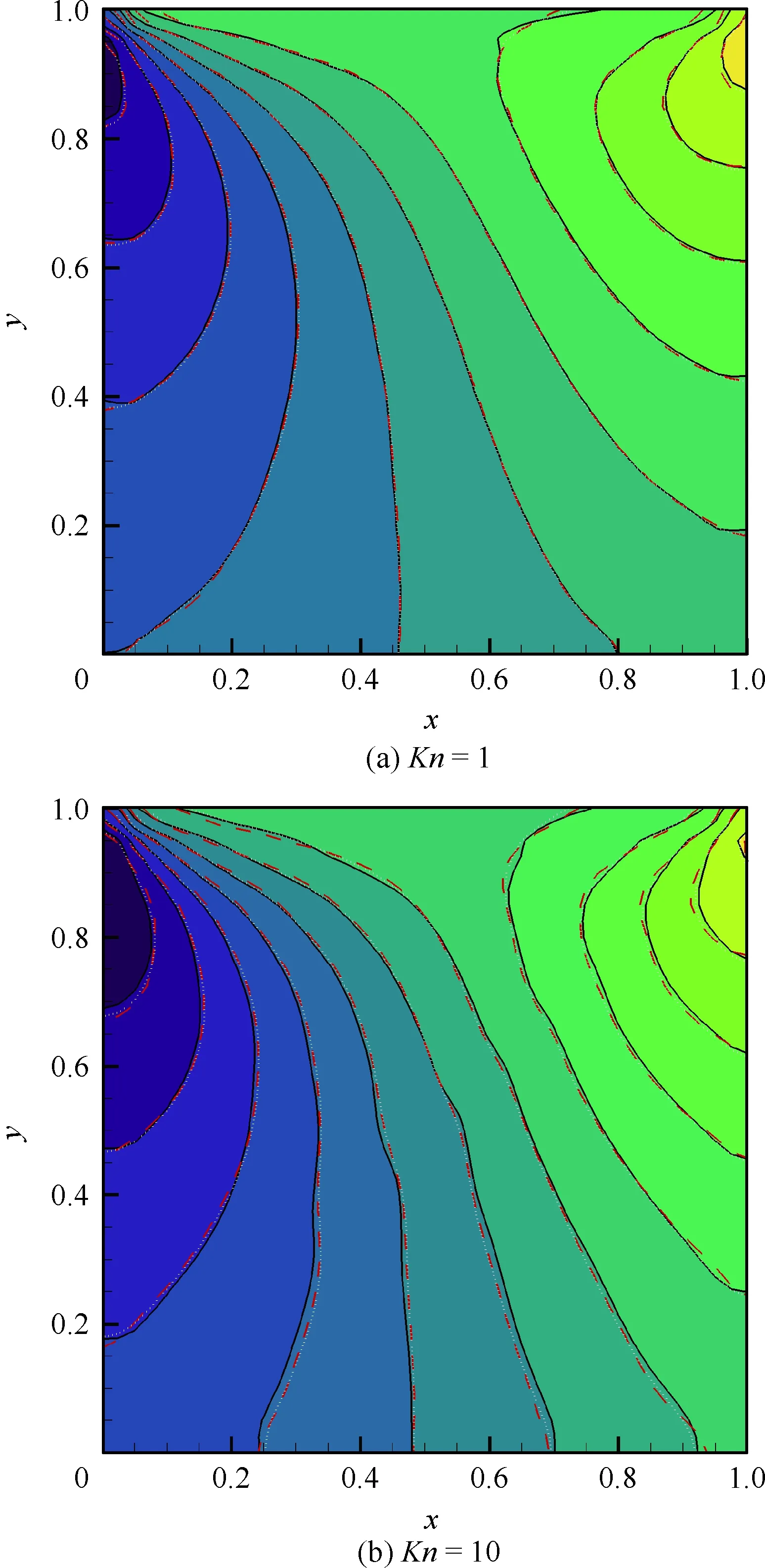
图4 采用不同方法计算的顶盖驱动流温度云图比较

表1 采用和不采用非结构网格速度空间和守恒修正IDVM迭代次数和计算时间的比较
3.2 高超声速圆柱绕流
该算例为Ma=10和Kn=0.003 03的高超声速圆柱绕流问题。其来流温度为T0=200 K,壁面温度固定为TW=500 K。动力学黏性系数采用方程(48)计算,并将参考黏性取为
(51)
式中:ρ0和R0分别为来流密度和圆柱半径。由此可得Ma、Re和Kn之间的关系如下:
(52)
计算时,物理空间采用100×80的结构网格进行离散。该算例如果速度空间采用四阶Newton-Cotes积分将需要约121×121个网格单元[23],而采用非结构网格时仅需要6 338个网格单元,内存开销小于原来的1/2。图5为所采用的速度空间非结构网格,中间的圆形范围为速度空间的加密区域。采用和不采用非结构网格速度空间和守恒修正IDVM计算该算例时所需的CPU时间分别为1.00 h和2.30 h。图6为采用IDVM计算的速度和温度云图。由于Kn数较小,在圆柱尾部可见两个反向的涡。图7比较了物面压力和应力分布,IDVM与DS2V和UGKS的结果[36]均吻合较好。另外,采用IDVM计算得到的阻力系数为1.259,其与DS2V的计算结果1.252和UGKS的计算结果1.258的相对误差均小于1%。

图5 高超声速圆柱绕流问题的速度空间非结构网格
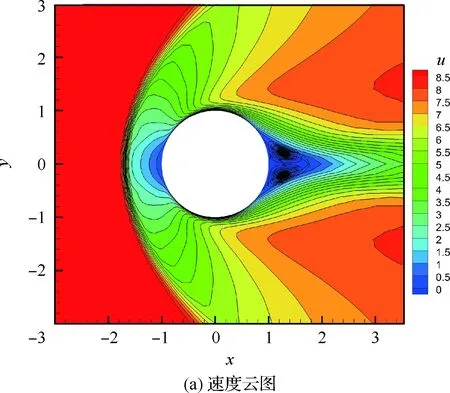
图6 采用IDVM计算的速度和温度云图
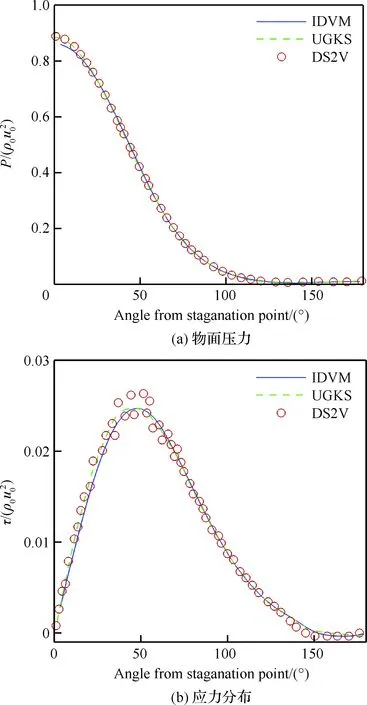
图7 圆柱表面压力和应力分布
3.3 超声速绕球流动
该算例为Ma=3.834和Kn=0.03的超声速绕球流动问题。来流无量纲温度取为T0=1,物面温度固定为TW=[1+(γ-1)Ma2/2]T0。动力学黏性系数采用w=0.75的变径硬球模型计算,物理空间采用包含20 736个六面体单元的非结构网格进行离散,速度空间采用包含36 053个四面体单元的非结构网格进行离散,如图8所示,中间的球形范围为速度空间的加密区域。计算的速度云图如图9所示。驻点线速度和温度分布如图10所示,IDVM与DSMC结果基本吻合。

图8 超声速绕球流动问题的速度空间非结构网格
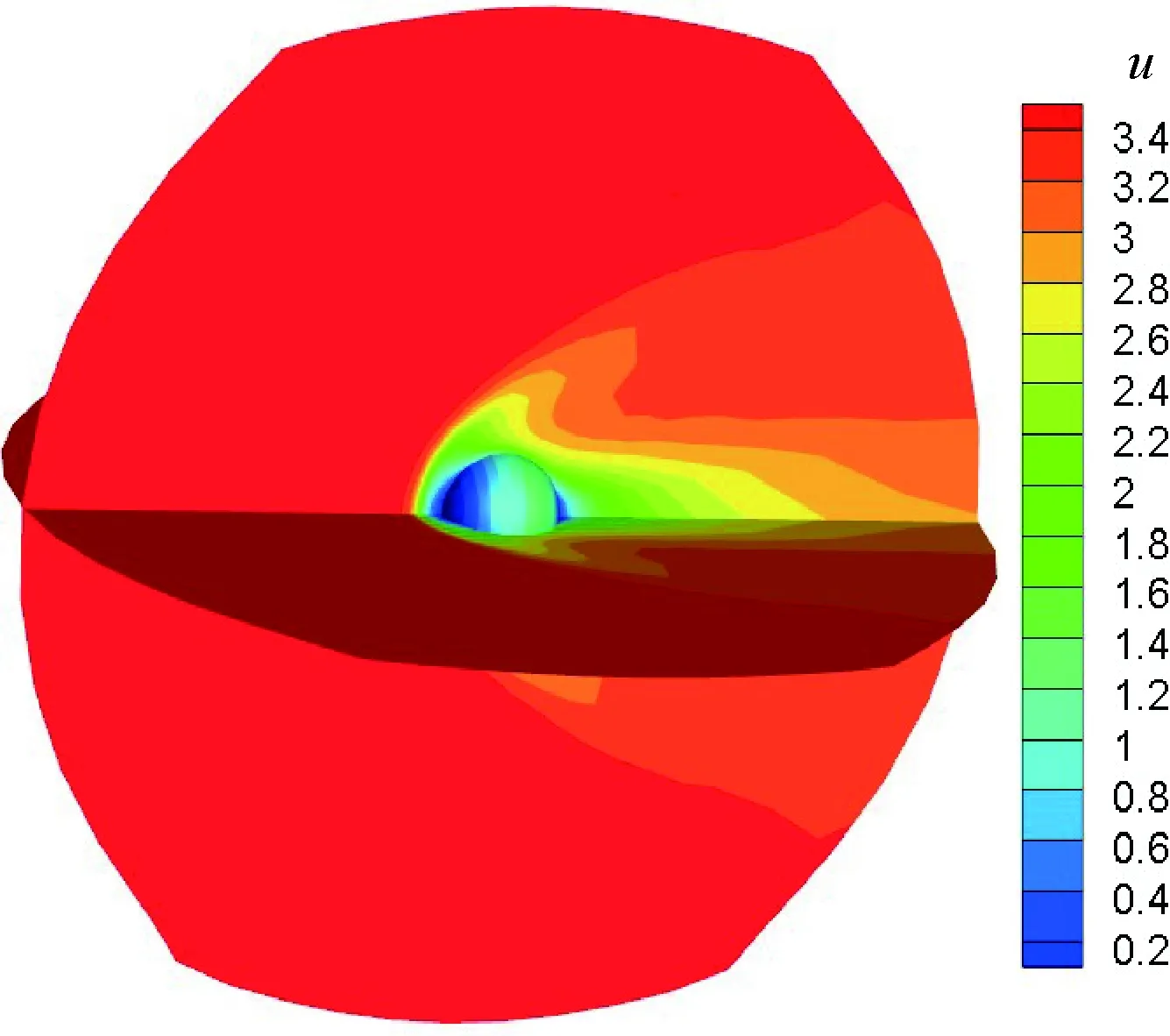
图9 采用IDVM计算的速度u云图
同时,采用IDVM计算的阻力系数为1.4295,与Li和Zhang[37]结果1.374 9以及DSMC结果1.412 2均吻合较好。此外,该算例采用了24线程的OpenMP并行计算时,总耗时为13.59 h。
4 结 论
本文提出了一种基于非结构网格速度空间和守恒修正的改进离散速度方法。
1) 当前算法在全流域范围均可获得准确的计算结果。
2) 采用非结构网格速度空间和守恒修正可以进一步提高IDVM的计算效率。
3) 采用非结构网格速度空间相较于基于四阶Newton-Cotes求积的内存开销更小。
