重庆市大健康产业人才需求回归预测模型的构建研究——基于主成分分析法的视角

骆永菊，王 珞

（重庆电子工程职业学院 财经管理学院，重庆 401331）

我国第一部《中国大健康产业发展蓝皮书（2018）》，将大健康产业界定为“以优美生态环境为基础，以健康产品制造业为支撑，以健康服务业为核心，通过产业融合发展满足社会健康需求的全产业链活动”［1］。大健康产业涵盖有机农业和中草药种植业；健康食品业、医药制造业、健康装备器材制造业；医疗卫生服务、环境和公共设施管理业、健康管理业、健康金融服务业等国民经济三大产业［2］1。近年来，业界进一步把大健康产业划分为“医、养、健、管、游、食”等六大产业，即健康医药医疗产业、健康养老产业、运动健身产业、健身管理产业、健康旅游产业和健康药食材产业［2］1。本文以医疗卫生服务业为例，研究重庆市大健康产业人才的需求情况。

《“健康中国2030”规划纲要》明确将发展健康产业作为健康中国建设五大任务之一，并提出将健康产业发展成为国民经济支柱性产业的战略目标。具体描述为，“2020年，建立覆盖城乡居民的中国特色基本医疗卫生制度，健康素养水平持续提高，健康服务体系完善高效，人人享有基本医疗卫生服务和基本体育健身服务，基本形成内涵丰富、结构合理的健康产业体系，主要健康指标居于中高收入国家前列。到2030年，促进全民健康的制度体系更加完善，健康领域发展更加协调，健康生活方式得到普及，健康服务质量和健康保障水平不断提高，健康产业繁荣发展，基本实现健康公平，主要健康指标进入高收入国家行列。到2050年，建成与社会主义现代化国家相适应的健康国家”［3］。

根据重庆市卫生健康委公布的数据，截至2020年，重庆市医疗卫生机构20922个，其中医院859个、基层医疗卫生机构19838个、专业公共卫生机构149个。每千人口医疗卫生机构床位数达到6.38张、执业（助理）医师数达到2.77人、注册护士达到3.41人，每万人口全科医生人数达到3.12人。

根据《重庆市医疗卫生服务体系“十四五”规划（2021—2025年）》，到2025年，重庆市每千人口执业（助理）医师数达到3.6人（中医类别达到0.8人）、注册护士达到4.7人、药师（士）数达到0.54人，每万人口全科医生数达到4人，每10万人口精神科执业（助理）医师数达到6人，康复医师数达到8人，每百张床位临床药师数达到0.7人，医疗机构药学专业技术人员不低于本机构卫生专业技术人员总数的8%。合理提高公共卫生人员配置标准，到2025年，每千人口专业公共机构人员数达到0.86人，社区卫生服务中心、乡镇卫生院和二级以上医疗机构配备公共卫生医师数不少于1人［4］。

为顺利完成《重庆市医疗卫生服务体系“十四五”规划（2021—2025年）》，如何确保合理的、可持续发展的健康服务人才的供给与布局，能够相对准确地、科学地进行一个国家或者是一个地区的健康产业人才的需求预测，明晰影响大健康产业人才需求的因素，就成为值得重点研究的问题之一。

一、指标的筛选

（一）资料的获取

本文依据现有的文献指标选择方法，结合各方面收集的资料和专家的意见，在考虑指标体系数据的获得性、适用性，以及不同行业研究对象的差异性，选取了宏观经济因素、社会环境因素、对外经济因素三类共计20个指标进行预测，具体见表1。

表1 重庆市人才需求预测解释变量（自变量）的指标初选

本文初步拟定以上20个指标作为自变量（即X1，…，X20），以重庆市卫生人员总量作为因变量（记为Y1）（表2、表3）。

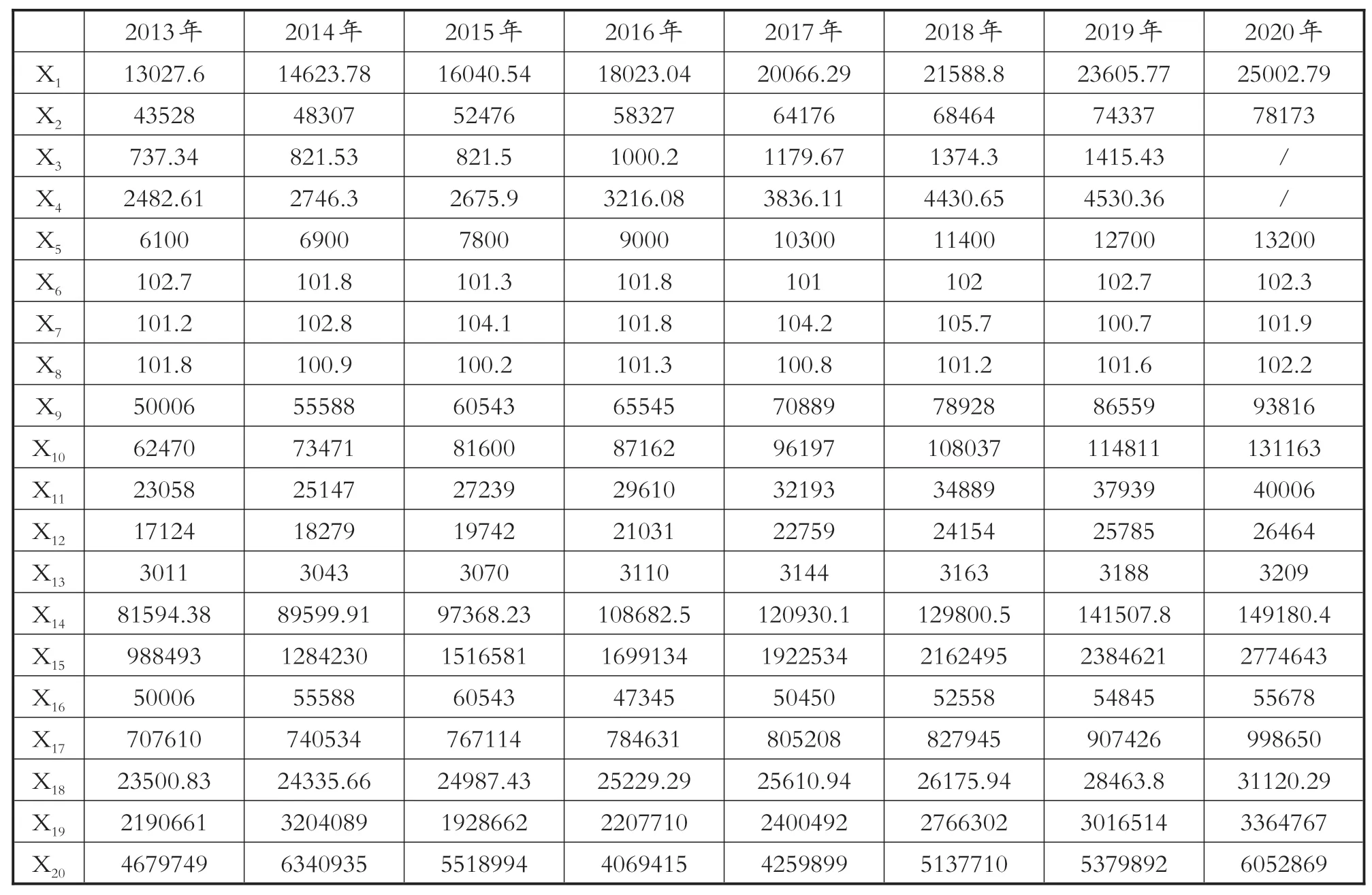
表2 重庆市2013年—2020年20个解释变量（自变量）的相关数据

表3 被解释变量（因变量）初选（单位：人）

（二）指标的筛选

1.剔除重复性指标

在所选的指标中，有总量指标，也有平均指标，而且有些指标是派生的，如全市卫生总费用和人均卫生总费用、全市国内生产总值与人均国内生产总值、全市普通高等教育在校学生数和全市百万人口高等教育学生平均在校生数就是派生关系，必然产生多重共线性。因此，二者只保留其一。由于多数指标是平均指标，因此，保留平均指标，剔除X1、X3、X15、X17，详见表4。

表4 初步筛选后的解释变量（自变量）

X5第三产业增加值除以国内生产总值转换为第三产业比重，得到相对指标。X4人均卫生总费用2020年数据缺失，由于样本量极其有限，因此，以前三期{0.2，0.3，0.5}的权重采取加权移动平均方法将该数据补上，整理后的解释变量的具体数据见表5。

表5 调整后的解释变量（自变量）数据

2.数据修正

为了研究的口径一致，将被解释变量（因变量）也调整为平均指标，将Y1到Y7都除以当年常住人口数，得到每万人拥有各类从事大健康工作的人员数。此时X2（全市人均国内生产总值）与X8（全市商品零售价格指数）重复。且X8与计算结果不符，予以剔除。调整后的数据见表6。

表6 调整后的被解释变量（因变量）数据

3.剔除相关性不显著的指标

对解释变量（自变量）和被解释变量（因变量）应用统计软件SPSS23.0中文版进行相关分析，得到的结果见表7。

从表7相关系数来看，在显著水平0.05的置信水平下，重庆市卫生人员总量与全市居民消费价格指数X6、全市医疗保健消费价格指数X7、全市商品零售价格指数X8、重庆市全员劳动生产率X14以及重庆市进出口总额X19X20的相关系数相关性不显著，予以剔除。其余指标与重庆市卫生人员总量具有极大的相关性，都在0.9以上。于是解释变量（自变量）个数由以前的16个缩减为现在的10个，见表8。

表7 相关分析数据表

4.剔除多重共线的指标

对表8进行共线性检验。需要说明的是，共线性检验是在回归中进行的。而回归要求样本量必须大于变量数+2，而表中的样本量小于变量数，因此，不会算出相关指标计算结果，需要先找出剔除的变量（表9）。

表8 去除相关性不显著变量后的数据表

表9 排除的变量a

检验结果排除X2全市人均国内生产总值、X12城镇居民人均可支配收入、X14全市全员劳动生产率（表10）。

二、主成分分析降维

为了解决自变量之间存在的共线性问题，同时尽可能多地保留人才需求影响因素的变量，本文采取主成分分析法构建回归模型。

由于表10仍不能满足样本量的要求，所以，对解释变量（自变量）进行降维处理（见表11）。

表10 去除共线变量后的数据表

表11 成分矩阵a

经过主成分分析后，分析结果只提取一个成分，即：

公 式（1）：F=0.968x4+0.964x5+0.998x9+0.993x10+x11+0.99x13+0.925x18

由公式（1）预测F的值为：（表12）

表12 重庆市2013年-2020年的F值

三、回归分析

以主成分分析提取的变量F为自变量，变成Y对F的一元回归。

Y1的回归结果如下表13：

表13 结果摘要

结果显示P值=5.03E-07，回归效果显著。即：

同理，可以求出：

根据回归结果，把（1）式F代入（2）—（8）式，预测重庆市2013—2020年每万人口卫生人员和大健康产业管理人员数，见表15。

由表15可以看出回归模型的实际值与预测值比较一致。根据表15，将实际值与预测值绘制成图，得到更直观的图形表示，见后（图1）。

从图1可以直观地看出重庆市卫生人员总量的预测值与实际值的变化趋势基本反映了实际值的变化趋势。由此判断，本文构建的回归预测模型用来预测重庆市卫生人员总量的预测值偏差较小，可靠度较高。

图1 重庆市每万人口卫生人员和大健康产业管理人员预测值与实际值对比

续表7

四、未来五年的预测值

表15预测是Yi分别对F0回归，F0以主成分系数与自变量的实际值的点积得到的。而未来五年没有自变量的实际值，因此，以F0的前8年的预测值为因变量值，以年代的顺序号为自变量，进行一元线性回归。需要说明的是，线性回归不能适用长期预测，因为每万人口健康工作人数不能无限制的增长，但对短期还是可以近似的。尽管如此，随着远离预测变量的平均值，其预测误差越大。

表15 重庆市每万人口卫生人员和大健康产业管理人员预测值与实际值对比

F的预测值及置信区间（表16）：

表16 以年份顺序号为自变量主成分F预测值及置信区间

以F为自变量，Y为因变量回归结果如表14，其置信上下限是两次回归的叠加。预测值以95%的概率置于上下限之间（表17）。

表14 七个因变量（Y）回归结果汇总表

表17 以主成分F预测值为自变量Y的预测值及置信区间

五、研究结论

本文利用主成分分析一元回归方法，构建了重庆市大健康产业的各类人才需求预测模型，经过实际数据计算，构建模型的预测值与实际值比较接近，预测效果较好。

图2 主成分F预测值及5%置信水平区间

图3 每万人口拥有的卫生人员总量预测值

但是需要说明的是，由于重庆统计年鉴（2022年）尚未公布，2021年的统计年鉴只体现了2020年的数据，所以，本文把2021—2022年也列入预测年里。同时，线性回归不能适用长期预测，因为每万人口健康工作人数不能无限制的增长。因此，随着远离预测变量的平均值，其预测误差越大。所以，本文只预测了未来几年的每万人口拥有的卫生人员总量预测值。

从前面研究可以看出，影响重庆市大健康产业的因素主要有城镇常住居民人均年可支配收入、卫生和社会工作人员平均工资、城镇非私营单位就业人员平均工资、第三产业增加值、全市常住人口、人均卫生总费用、全市百万人口高等教育学生平均在校生数，如表18。

表18 每万人口拥有卫生人员总量相关因素相关程度降序排序