摩擦热和夹杂对高速微型球轴承接触亚表面裂纹萌生的影响

方群，李锦棒,，刘凯，王国荣，崔玉国

(1.宁波大学 机械工程与力学学院，浙江 宁波 315211；2.宁波达尔机械科技有限公司，浙江 宁波 315202；

3.西南石油大学 机电工程学院，成都 610500)

随着机械设备向高速重载方向发展，服役轴承面临着重大挑战[1-4]。轴承在高速工况下的实际寿命往往远小于设计寿命，其接触表面通常会出现早期的剥落失效[5-8]。研究发现，球轴承在高速重载条件下亚表面易产生微裂纹形成疲劳源，扩展至表面形成剥落，进而慢慢出现大面积表面剥落[9-12]。高速球轴承接触部位会产生极高的接触应力和摩擦热，循环往复的接触应力是球轴承疲劳失效的主要原因[13-15]。

对于轴承的接触疲劳失效，国内外学者从接触表面剥落，微观结构演化，裂纹萌生及扩展等方面进行了大量研究：文献[16]通过试验研究了接触载荷对滚动接触损伤行为的影响，发现球与沟道接触表面易萌生裂纹并向亚表面进行扩展；文献[17]结合有限元法与断裂力学理论对钢轨滚动接触疲劳裂纹进行应力分析，并利用应力强度因子描述裂缝尖端的应力场；文献[18]在循环载荷作用下建立模拟损伤的模型，得到循环载荷与损伤变量的关系，利用曲线拟合参数验证试验结果；文献[19]采用扩展有限元法与内聚力单元相结合的方法研究了载荷加载方向对复合型裂纹扩展的影响；文献[20-22]基于概念数据模型的方法模拟钢轨滚动接触中材料亚表层裂纹的萌生和扩展。以上皆是在滚动速度较小的工况下进行的数值模拟和试验分析，大多将剪应力视为疲劳寿命预测中起主导作用的失效应力，结合数值计算对亚表面裂纹萌生和扩展进行模拟，并未研究在高速工况下摩擦生热、材料夹杂硬度对数值分析结果的影响。

鉴于此，本文提出一种在高速工况下新的数值分析方法，设置可以热力耦合的内聚力单元，考虑摩擦热和不同硬度的夹杂，并观察其对整个微观结构的影响。首先，应用循环迭代法通过Fortran语言对轴承径向、轴向载荷进行编译，在Visual Studio上运行模拟载荷并加载到有限元仿真软件中，得到联合载荷与应力场的关系；其次，在球轴承与内外圈沟道的接触区域亚表面建立0厚度的内聚区模型，设置具有温度自由度的内聚力单元；最后，编写Python随机插入圆形夹杂并引入摩擦生热的温度场进行热力耦合分析。通过对高速工况下球轴承接触亚表面裂纹萌生的微观研究，基于断裂力学和损伤力学数值分析，将轴承微观温升数值结果与宏观试验结果进行比较，为高速球轴承接触区域微观机理分析提供模型支撑。

1 理论模型的构建

深沟球轴承球与内外圈接触，其赫兹接触状态决定了接触区域各点处的应力、应变状态，且接触应力的分布呈高度的局域性。球与沟道接触区域微观模型如图1所示，模拟了球与沟道接触处的表面下方即亚表面处的接触状态，图中：Fr为径向载荷，Fa为轴向载荷，P为载荷应力。建立赫兹接触状态下的应力应变与内聚力单元中的拉力分离之间的本构关系，为使模型可以忽略黏结处的分层，选用基于拉力-分离(σ-δ)的0厚度内聚力单元，通过自定义Python脚本实现在任意实体单元间对模型全局插入0厚度的内聚力单元，如图2所示。

图1 球与沟道接触区域微观模型图Fig.1 Micro model diagram of contact area between ball and raceway

图2 实体单元间插入内聚力单元Fig.2 Inserting cohesive elements between solid elements

用拉力-分离(σ-δ)方程代替工程中应力-应变(σ-ε)方程，内聚力单元应力传递关系如图3所示，α为裂纹张开角度。

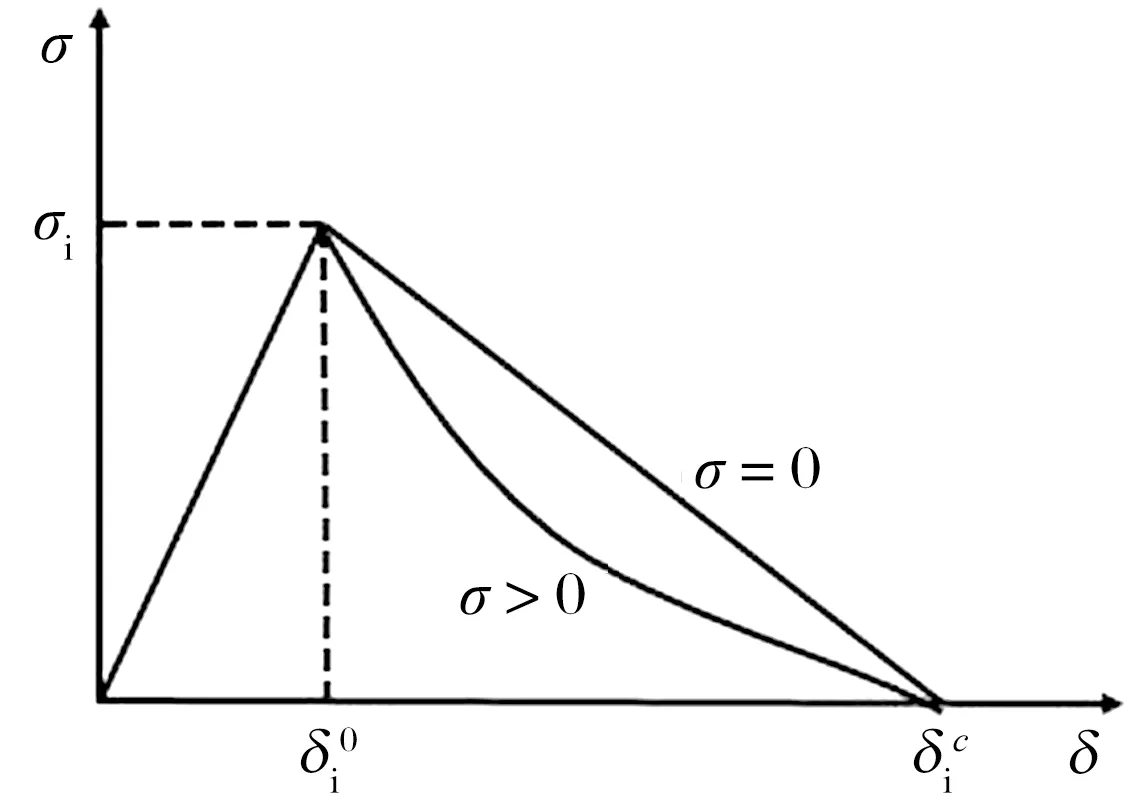
图3 内聚力单元应力传递关系Fig.3 Stress transfer relation of cohesive elements

基于损伤力学与断裂力学公式[23]，应力与分离距离的关系为

σi=Kiδi，

式中：σi为表面应力；Ki为材料刚度；δi为分离距离。

材料刚度与损伤变量的关系为

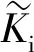
损伤初始准则为

损伤起始后的分离距离为

在ABAQUS中，弹性刚度的退化可以通过损伤变量来表示。损伤变量(退化刚度SDEG)为

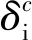
2 数值模拟

2.1 模型的建立

本文使用有限元分析软件ABAQUS模拟高速球轴承接触微观区域，创建长0.2 mm、宽0.1 mm的二维平面表示球与沟道接触区域，在模型几何中心靠近表面处进行分区细化，设定分区长为0.14 mm，宽为0.07 mm。网格类型为双线性四节点的四边形单元(CPE4R)，为提高计算收敛性，采用减缩积分和沙漏控制。中间分区部位网格单元设置为0.5 μm，其他部分网格大小由内向外从0.5 μm到1 μm递增，网格总数为18 207，节点数为36 911。球与沟道接触区域的网格划分如图4所示。

图4 球与沟道接触区域的网格划分Fig.4 Meshing of contact area between ball and raceway

模型材料参数见表1，内聚力单元的材料参数见表2。

表1 模型材料参数Tab.1 Model material parameters

表2 内聚力单元材料参数Tab.2 Material parameters of cohesive elements

2.2 联合载荷下的接触应力

为模拟高速球轴承在接触微观区域的受力情况，首先应用循环迭代法通过Fortran语言对轴承径向、轴向载荷进行编程，接着在Visual Studio中进行模拟计算，最后加载到有限元仿真软件建立的接触区域模型中，即可得到联合载荷作用下球轴承微观接触区的应力场分布。

仿真中的载荷为压力，压力施加的起点为-0.02 mm，每一分析步压力作用区域移动的距离为0.006 mm，即球轴承运转速度为10 000 r/min，径向压力和轴向压力的初始值设为P0=2 GPa。为探究径向压力与轴向压力对亚表面处最大接触应力的影响，轴向压力为初始值时，径向压力分别设置为1，2，3 GPa；径向压力为初始值时，轴向压力分别设置为1，2，3 GPa。径向、轴向压力分别与亚表面最大接触应力之间的关系如图5所示：随着轴承转数的累加，接触应力均略微上升；增大径向压力，接触应力也随之较大幅度增大，增大轴向压力，接触应力先增大后减小；两者对比反映出径向压力对接触应力的影响占主导地位。

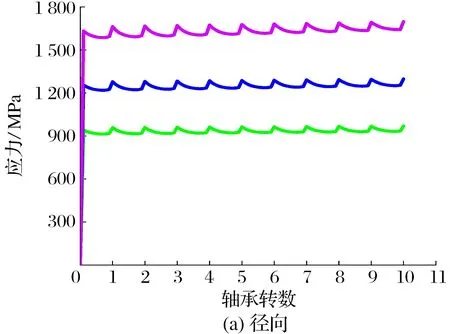
图5 联合载荷与接触应力的关系Fig.5 Relationship between combined load and contact stress

径向压力作用下接触区域的应力场分布如图6所示：在接触区域无损伤的情况下，最大接触应力在接触表面下方即亚表面。这与赫兹接触理论恰好吻合，为后续裂纹分析提供依据。在联合载荷作用下，当亚表面的内部应力大于材料的损伤极限应力时便会产生疲劳损伤累积。

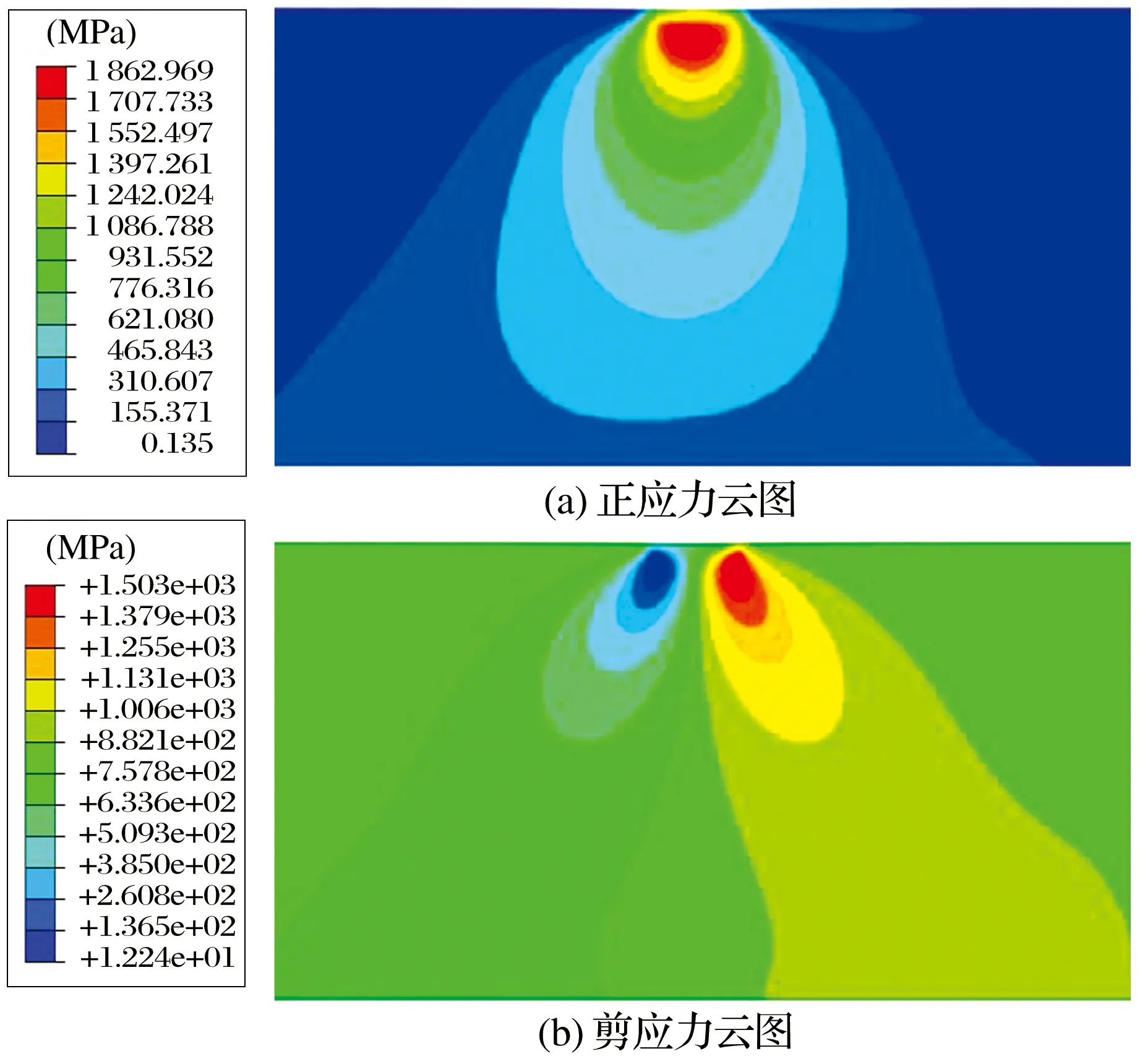
图6 径向压力作用下接触区域的应力场分布Fig.6 Stress field distribution in contact area under radial load

2.3 夹杂与温升对亚表面裂纹的影响

编写Python脚本在微观接触模型亚表面内聚区随机插入半径为r=3 μm、材料为硫化锰和氧化铝的圆形夹杂，如图7所示。硫化锰的弹性模量为138 GPa，泊松比为0.3；氧化铝的弹性模量为375 GPa，泊松比为0.23。在模型上施加载荷进行应力分析，并开发可以进行热力耦合的内聚力单元。在有限元模型文件里定义接触摩擦生热、对流换热、热传导和辐射换热，在接触属性中设置滚动接触的摩擦生热及初始温度，改变模型文件单元类型，设置可实现内聚力单元传热的热单元。

图7 随机插入的圆形夹杂Fig.7 Randomly inserted circular inclusions

当损伤变量达到1时，不同夹杂的应力云图及亚表面处最大应力位置变化如图8所示，氧化铝夹杂边界刚度退化情况如图9所示。

(a) 硫化锰夹杂

图9 氧化铝夹杂边界刚度退化Fig.9 Boundary stiffness degradation of alumina inclusions

由图8可知，引入夹杂后亚表面处的最大接触应力的位置与未引入夹杂时最大接触应力的位置相比更靠近接触表面；对于硫化锰夹杂，亚表面最大接触应力位置距离接触表面7.5 μm，向上偏移4.8 μm；对于氧化铝夹杂，亚表面最大接触应力位置距离接触表面7.7 μm，向上偏移4.6 μm；随着深度的增加，应力减小，夹杂材料对应力值和应力分布有着显著影响。由图9可知，损伤变量已达到1，根据断裂力学此时裂纹开始出现；放大观察夹杂边界的刚度退化可以看出离亚表面越远的区域，裂纹萌生的概率越小；离亚表面越近的区域，裂纹萌生的概率越大。通过对不同材料夹杂的模拟，可看出接触区域裂纹的萌生主要由亚表面最大应力的位置及其向外衰减的趋势所决定。将夹杂材料设为较软的氧化铝后，接触区域的最大应力数值有所下降，与材料较硬的夹杂相比，较软的夹杂边界不易萌生裂纹。

其他条件不变，引入温度场进行热力耦合分析，摩擦生热后的应力云图和热流量云图如图10所示。摩擦生热条件下，最大接触应力位置与接触表面几乎重合，并且夹杂边界出现了一定程度的应力集中。结合图9与图10可以看出，热流与夹杂交汇处的边界易形成裂纹且裂纹大多在夹杂的左右两端。

(a) 热应力云图

引入摩擦前后损伤变量随轴承转数的变化关系如图11所示，在相同的轴承转数下，考虑摩擦生热影响的曲线会更快达到损伤变量1(损伤阈值)，即达到裂纹开裂状态，因此摩擦热对球轴承裂纹的萌生起促进作用。

在联合载荷作用下，接触亚表面裂纹和夹杂附近应力分布如图12所示，接触亚表面的裂纹和夹杂附近出现“蝴蝶”形应力分布，这与已有研究[24]发现的起源于次表面夹杂物的蝶状组织一致，说明了模型的正确性。

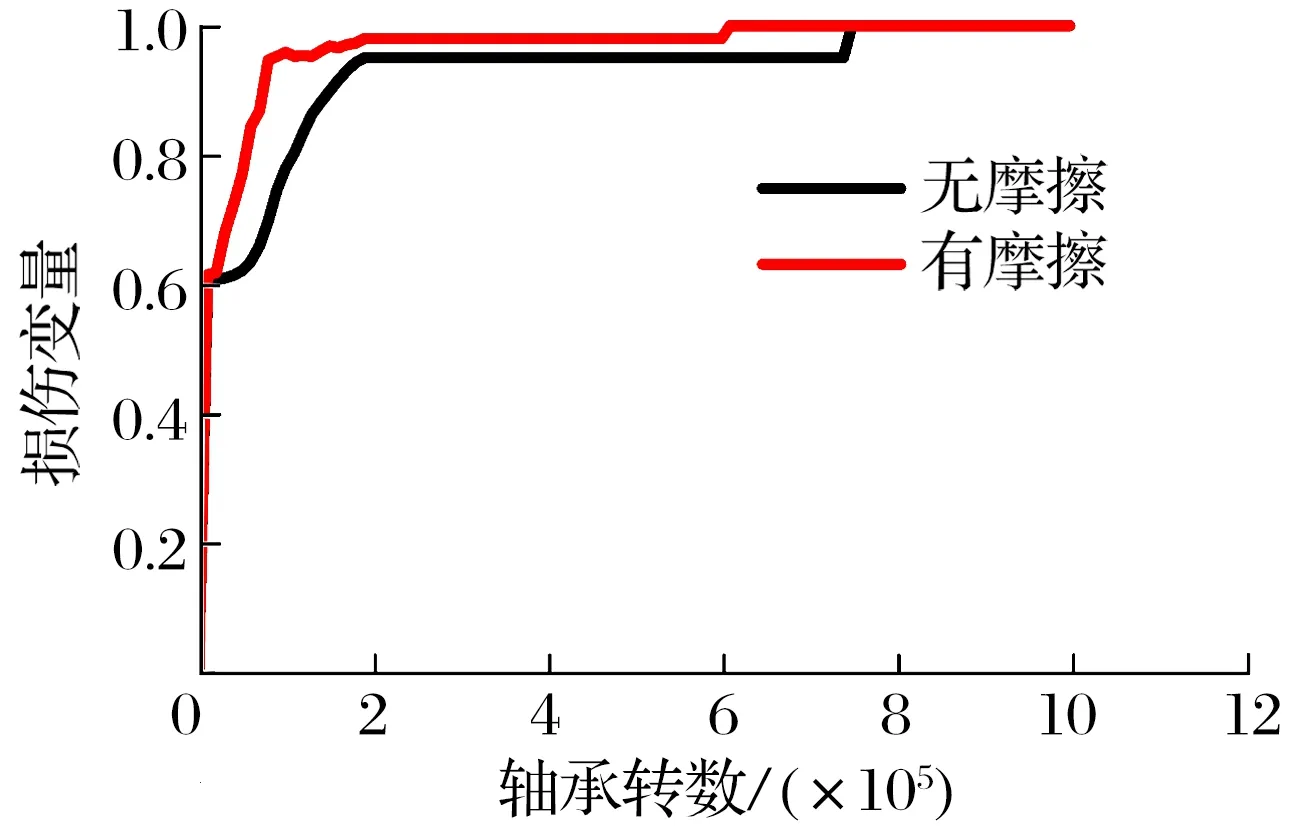
图11 引入摩擦前后损伤变量随轴承转数的变化Fig.11 Variation of damage variable with bearing rotation before and after introducing friction

图12 联合载荷作用下接触亚表面裂纹和夹杂附近应力分布Fig.12 Stress distribution near contact subsurface cracks and inclusions under combined load

3 试验验证

为验证模型的有效性，进行温度试验，使用的T3-8N/2双工位球轴承疲劳寿命试验机如图13所示，主要由试验机主体、动力系统、加载系统、润滑系统、电气控制系统、计算机监控系统等组成。采用608深沟球轴承，通过试验机的加载螺母加载径向载荷和轴向载荷，循环105次。试验机采用计算机自动控制，可自动采样与存储数据。

图13 高速球轴承疲劳寿命试验机Fig.13 High-speed ball bearing fatigue life tester

转速为10 000 r/min时，轴向载荷为25 N，径向载荷分别为50，100，150，200 N，轴承试验温度与数值仿真模型温度的变化如图14a所示。转速为10 000 r/min时，径向载荷为25 N，轴向载荷分别为50，100，150，200 N，轴承试验温度与数值仿真模型温度的变化如图14b所示。

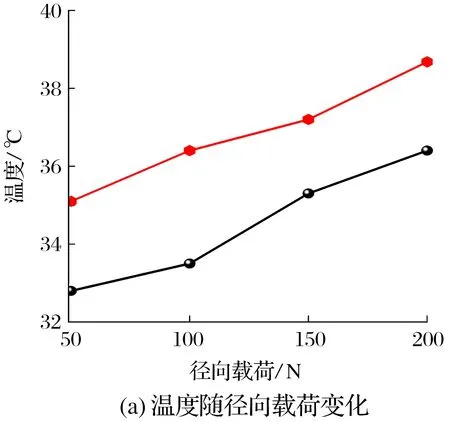
图14 轴承试验温度与数值仿真模型温度随载荷的变化Fig.14 Variation of bearing test temperature and numerical simulation model temperature with load

由图14可知，数值模型温度略大于试验温度。这是因为试验检测到的是轴承外圈温度，无法检测到内圈沟道处温度，故而造成温度偏小。但就总体趋势而言，试验数据与数值模型数据具有较高的一致性，反映出所建高速球轴承接触微观区域数值仿真模型的合理性。

4 结论

本文以高速工况下球轴承接触微观区域为研究对象，将赫兹接触与基于损伤力学的内聚力单元本构关系作为理论基础，建立高速球轴承微观接触区域模型，分析球轴承接触微观区域亚表面应力场的分布、夹杂与温升对裂纹的影响，主要结论如下：

1)高速球轴承接触微观区域在联合载荷作用下，径向载荷对接触应力的影响占主导地位，接触区域裂纹的萌生主要是由亚表面最大接触应力的位置以及其向外衰减的趋势所决定。

2)夹杂使亚表面处最大接触应力的位置向上移动，随着深度的增加，应力减小，刚度退化衰减；距离亚表面越远的区域裂纹萌生的概率较小，距离亚表面越近的区域裂纹萌生的概率较大；与材料较硬的夹杂相比，较软的夹杂边界不易萌生裂纹。

3)在摩擦生热的条件下，夹杂边界出现一定程度的应力集中，热流与夹杂交汇处的边界上易形成裂纹且裂纹大多在夹杂的左右两端，摩擦热对球轴承裂纹的萌生起促进作用。