直升机传动系统离合器支承球轴承微动磨损分析
2023-01-09殷锐杨奉霖陈兴明尹美
殷锐,杨奉霖,陈兴明,尹美
(中国航发湖南动力机械研究所,湖南 株洲 412002)
1 概述
据统计,直升机传动系统工作时离合器大部分时间(约99%)处于接合状态,该工作状态下离合器支承球轴承内、外圈一起转动,内、外圈及球之间无相对转动,在离合器组件重力和振动载荷作用下,球与沟道之间的润滑油膜会破裂,导致球与沟道直接接触,沟道接触区域附近易发生微动磨损[1](图1),进而导致轴承旋转精度下降,振动和噪声增大,严重影响轴承服役性能。
国内外关于轴承微动磨损的研究有:文献[2]通过试验得到了轴承内圈与端盖接触面之间的压力分布;文献[3]认为发生在轴承接触区域的微动磨损分别为微动腐蚀和伪压痕;文献[4]采用接触区域切向力和相对滑动速度的乘积表征轴承微动磨损的损伤程度;文献[5]通过试验分析了载荷、摆动角度和循环次数对角接触球轴承微动磨损的影响,结果表明套圈微动磨损随摆动角度增大而加重,随循环次数增加,其磨损程度增加,磨损速度趋缓;文献[6]基于Archard磨损理论建立球轴承的磨损寿命模型,分析了预载荷和磨损系数的关系,结果表明相同初始预紧力下接触应力与滑动速度的乘积随摩擦因数增大而减小。

图1 离合器支承球轴承沟道磨损痕迹Fig.1 Wear trace on raceway of ball bearing supporting clutch
在上述研究的基础上,本文基于Archard方程的思想建立球轴承微动磨损计算模型,并分析球直径和套圈沟曲率半径系数(fi=fe)对轴承微动磨损的影响。
2 球轴承微动磨损量计算模型及试验验证
2.1 计算模型
由Archard 黏着磨损定律可得[7]
(1)
式中:ΔV为磨损体积;S为磨损距离;ks为黏着磨损常数;F为施加的载荷;δs为软材料的受压屈服极限。
接触面(图2)上任意一点的压应力为[8]
(2)
式中:p0为接触区域最大接触压应力;Q为球与沟道的法向接触载荷;a,b分别为接触椭圆的长、短半轴。

图2 球与沟道的接触椭圆示意图Fig.2 Diagram of contact ellipse between ball and raceway
轴承接触中心压应力最大,滑动量为0。轴承受载后,滚动过程中在接触椭圆上任意一点套圈和球的位移分别为
(3)
(4)
式中:θr,θw分别为套圈和球的转动角度;dr为沟道直径;Dw为球直径;Δd如图3所示。
球与套圈的相对滑动距离为
Sc=Sw-Sr。
(5)

图3 球与沟道的相对移动示意图Fig.3 Diagram of relative displacement between ball and raceway
接触区任意一点单位面积的磨损量ΔV(x,y)为
(6)
对(6)式二重积分可得总磨损体积
(7)
(7)式为球轴承接触椭圆区域上整体磨损量的微动磨损评价公式。通过修正既有的Archard磨损模型,采用FORTRAN语言编写ABAQUS用户子程序UMESHMOTION,提取接触区域的力学响应参数,计算接触区域各单元节点的磨损量,并结合任意拉格朗日-欧拉自适应网格技术,更新接触区域的网格节点,通过重复提取单元节点信息参数进行迭代计算,实现模拟磨损过程。计算流程如图4所示。

图4 球轴承磨损量计算流程图Fig.4 Flow chart for calculation of wear amount of ball bearing
2.2 试验验证
以某深沟球轴承为例分析,其主要结构参数为:内径60 mm,外径95 mm,宽度11 mm,球直径7.144 mm,球数19,套圈沟曲率半径系数0.51,接触角为0°。球和套圈材料均为GCr15轴承钢,材料参数为:弹性模量207 GPa,泊松比0.3,黏着磨损常数5×10-5,材料屈服极限1 500 MPa。
本文利用球/平面微动磨损模型验证轴承磨损量的计算方法,有限元分析中定义一个瞬时动态隐式加载步,选取对应的频率建立分析步时长及最小增量步,切向行为的摩擦因数为0.001。在轴承内表面施加一个幅值为263 N的正弦函数载荷,模拟离合器支承球轴承实际工作中的高频振动。
分别给球加载4,8,12 N的力,模拟高频振动引起的球对套圈的冲击,接触区域磨损形貌如图5所示(红色区域为初始状态,蓝色越深代表磨损深度越大),沿x方向上的磨损深度如图6所示,接触区域及最大接触应力见表1。

(a) 4 N

图6 不同载荷下沿x方向的磨损深度Fig.6 Wear depth along x direction under different loads

表1 不同载荷下接触区域大小及最大接触应力Tab.1 Size of contact area and maximum contact stress under different loads
采用摩擦磨损试验机进行微动磨损试验[9],如图7所示,试样块与直径为7.144 mm的球材料均为GCr15,表面硬度均为60~64 HRC,在装有球的部件上施加法向载荷,控制试样块在水平方向上以频率2 Hz、位移100 μm往复移动50 000次。

图7 摩擦磨损试验机Fig.7 Friction and wear tester
试样块磨损形貌如图8所示,对磨损形貌进行白光干涉[10]可得试样块沿x方向的磨损深度如图9所示,与有限元分析结果一致,说明了本文微动磨损模型的正确性。

(a) 4 N (b) 8 N (c) 12 N图8 不同载荷下试样块的磨损形貌Fig.8 Wear morphology of test block under different loads

图9 不同载荷下试样块沿x方向的磨损深度Fig.9 Wear depth of test block along x direction under different loads
3 结构参数对球轴承微动磨损的影响
3.1 球直径
其他参数不变,仅改变球直径时接触椭圆区域沿x方向(y=0)的接触应力如图10所示,不同球直径时接触区大小及最大接触应力见表2,随球直径增大,接触区域面积增大,最大接触应力减小。通过(7)式可得不同球直径时接触椭圆区域沿x方向的磨损量,如图11所示,随球直径增大,接触区中心应力减小,最大磨损量减小。

图10 不同球直径时接触椭圆区域沿x方向的应力分布Fig.10 Stress distribution of elliptical contact area along x direction under different ball diameters
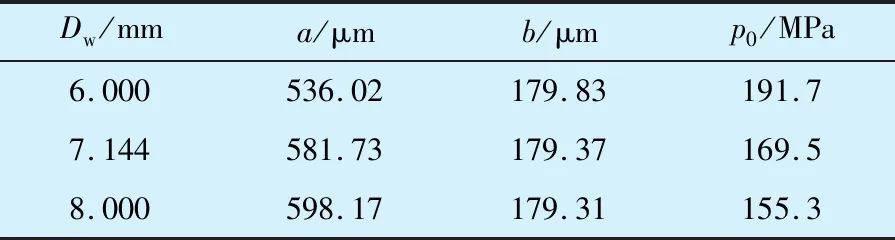
表2 不同球直径时接触区域大小及最大接触应力Tab.2 Size of contact area and maximum contact stress under different ball diameters

图11 不同球直径时接触椭圆区域沿x方向的磨损量Fig.11 Wear amount of elliptical contact area along x direction under different ball diameters
3.2 套圈沟曲率半径系数
其他参数不变,仅改变套圈沟曲率半径系数时接触椭圆区域沿x方向(y=0)的接触应力如图12所示,不同套圈沟曲率半径系数时接触区大小及最大接触应力见表3,沟曲率半径系数增大,接触区最大接触应力增大。通过(7)式可得不同沟曲率半径系数时接触椭圆区域沿x方向的磨损量,如图13所示,随套圈沟曲率半径系数增大,最大磨损量增大。
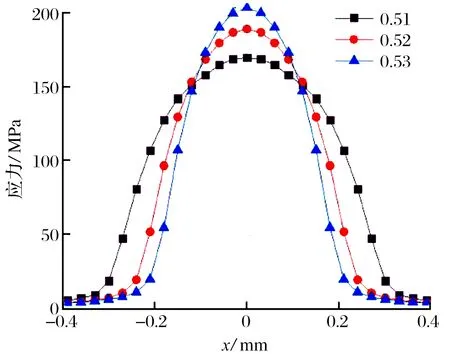
图12 不同套圈沟曲率半径系数时接触椭圆区域沿x方向的应力分布Fig.12 Stress distribution of elliptical contact area along x direction under different ring groove curvature radius coefficients

表3 不同套圈沟曲率半径系数时接触区域大小及 最大接触应力Tab.3 Size of contact area and maximum contact stress under different ring groove curvature radius coefficients

图13 不同套圈沟曲率半径系数时接触椭圆区域沿x方向的磨损量Fig.13 Wear amount of elliptical contact area along x direction under different ring groove curvature radius coefficients
4 结论
建立离合器支承球轴承微动磨损计算模型,分析了球直径和套圈沟曲率半径系数对轴承微动磨损的影响,得到以下结论:
1)随球直径增大,接触区面积增大,最大接触应力减小,微动磨损量减小;
2)随套圈沟曲率半径系数增大,接触区面积减小,接触应力增大,微动磨损量增大。
