中国USLE/RUSLE因子研究
2023-01-09马春玲戈文艳丁文斌刘元昊尚天赦曹乐乐林媛媛
马春玲, 焦 峰,2, 王 飞,2, 戈文艳,2, 丁文斌,刘元昊, 尚天赦, 曹乐乐, 林媛媛
(1.西北农林科技大学 水土保持研究所 黄土高原土壤侵蚀与旱地农业国家重点实验室,陕西 杨凌 712100; 2.中国科学院 水利部 水土保持研究所, 陕西 杨凌 712100)
土壤侵蚀破坏土地资源,进而引起水土流失,导致大量泥沙进入江河湖库,引起洪涝灾害、水体污染等环境问题,造成生态环境退化[1]。认识并了解土壤侵蚀的过程及机理,揭示引起侵蚀的因子与土壤性质之间的关系,并对土壤侵蚀进行准确的评估、监测和预报,有助于识别土壤侵蚀的易发区和水土流失治理的薄弱环节,从而指导水土保持措施配置,优化水土资源利用。利用土壤侵蚀模型对土壤侵蚀进行监测与预报,是土壤侵蚀评估的重要手段之一[2]。通用土壤流失方程(Universal Soil Loss Equation)及其改进版RUSLE,在过去40 a,已在109个国家被应用,是全球应用最为广泛的土壤侵蚀模型[3]。
USLE最初用于定量预报农地或草地坡面多年平均年土壤流失量,后来延伸至其他土地利用类型。美国农业部在80年代对模型进行修改,考虑了细沟和细沟间侵蚀;1997年又出版了修订通用土壤流失方程 RUSLE,改进了各因子的计算方法[4]。然而,它在模型结构上仍然存在局限性,只反映了相乘因子之间有限的相互作用和相互关系[2]。同时,USLE/RUSLE在进行侵蚀热点区识别和侵蚀潜力研究中有较好表现,对于土壤侵蚀过程和精确侵蚀量研究存在较大不确定性。
土壤侵蚀是一个复杂的多因子耦合过程,土壤侵蚀模型存在不确定性,无法解释沉积物输送的所有相互作用。USLE/RUSLE并不能表征所有形式和尺度的土壤侵蚀过程,例如无法解释沟壑侵蚀、河岸侵蚀等[5];另外,USLE/RUSLE系列以年为时间尺度衡量单位面积的土壤流失,无法衡量基于次降雨事件的土壤流失情况[6]。
20世纪末,USLE/RUSLE被引入中国。我国学者在USLE/RUSLE各因子计算方法修订和利用方程进行土壤侵蚀的监测和预报等方面进行了大量研究,有力推动了我国土壤侵蚀研究的进展。有学者根据我国的实测资料,提出了适用于黄土地区、东北地区、滇东北山区以及南方红壤区等区域土壤流失方程[7-9]。刘宝元基于1 841个地块年数据,在考虑中国陡坡水土流失的特点和系统性水土保持措施的基础上,提出了中国土壤流失方程(CSLE),用以预测不同水土保持措施下坡耕地的年平均土壤流失量。其中采用生物、工程和耕作措施因子代替作物覆盖与管理因子和耕作措施因子。但由于方程本身的局限性或研究人员对方程理解上的偏差等,在应用过程中不乏误用、错用等情况[4]。另外,各因子有严格的适用条件,计算方法有明显的区域适用性,加上我国土壤侵蚀的复杂性、基础数据缺失等[2],为方程的区域适用性评价增加了难度。
本文通过CNKI中国学术期刊全文数据库、Web of Science,以各因子的中英文表达、USLE、RUSLE为主题词,检索1965—2020年已公开发表的期刊论文,通过筛选与补充,共获得373篇相关文献。对这些文献进行综合分析,阐明USLE/RUSLE各因子常用计算方法的差异和优缺点,以及不同方法在计算过程中的限制条件,并就中国在各因子的计算及方程应用中存在的问题进行发现、总结,以期为USLE/RUSLE的应用优化及突破提供参考。
1 降雨侵蚀力因子(R)
1.1 标准定义及主要计算方法
降雨侵蚀力是指降雨引起土壤侵蚀的潜在能力,是评价降雨对土壤剥离、搬运侵蚀的动力指标。Wischmeier等[10]基于8 000多个地块的降雨、土壤侵蚀实测资料,回归分析发现降雨动能E和最大30 min雨强I30的乘积与土壤流失量的相关性最好,故用EI30计算多年平均降雨侵蚀力,并在USLE中得到应用。但由于不同地区降雨特性存在差异,EI30并非适用于全球。Hudson研究发现,相比EI30,KE>25法(以雨强I>25 mm/h的降雨总动能代表降雨侵蚀力)更适合热带亚热带地区[11]。Foster等[12]研究显示EI30与PI30(P指次降雨量)有高度线性相关,可以采用PI30来计算年降雨侵蚀力;且包含雨量、雨强和径流量的复合指标比EI30要好,认为径流量少降雨量大时EI30计算的降雨侵蚀力值偏高,反之则偏低,但径流数据获取困难。我国学者研究发现,中国北方地区EI30和EI10预测效果较好,南方地区EI60预测效果较好。王万中等[13]发现,进行全国性或大区域研究时,EI30整体的预报效果优于其他指标,而在降雨资料缺乏时可采用PI30。
以上计算方法均需要降雨过程资料,资料的年限最好为20年以上,很多地区缺乏这些资料。另外,降雨动能计算和断点雨强划分也较为麻烦,推广受到限制,因此有学者提出了降雨侵蚀力的简易算法,即通过建立常规降雨资料(降雨量等)与多年平均降雨侵蚀力之间的数量关系式来估算降雨侵蚀力。章文波等[14]参考Richardson等以日降雨量估算半月降雨侵蚀力的幂函数形式模型,建立了适合中国的半月降雨侵蚀力估算模型。后又基于逐年日雨量、逐年月雨量、逐年年雨量、月平均雨量及年平均雨量建立了其他降雨资料的模型。我国学者根据中国不同区域适宜的经典指标,利用常规降雨资料建立了大量的降雨侵蚀力简易估算模型。目前,我国R因子的简易估算模型主要有基于日降雨量、月降雨量、年降雨量的侵蚀力模型,也有包含雨量和其他降雨指标的复合指标模型,基本覆盖了我国主要水力侵蚀区。在研究全国或者大区域研究时,可引用章文波等[14]建立的日降雨量侵蚀模型;东南地区可参考吴素业[15]、郭新波等[16]]建立的模型;北京地区可参考徐丽等[17]建立的估算模型;西南地区可参考黄凤琴等[18]建立的估算模型;西北地区可参考刘秉正[19]、赵文武[20]等建立的模型。另外,基于不同分辨率降雨数据建立的简易模型所反映的降雨侵蚀力特征不同。研究者可根据研究区域、降雨数据的分辨率以及研究目的进行引用,并进行适用性验证。
1.2 R因子方程在中国的应用
基于对102篇流域或区域尺度土壤侵蚀或R因子文献研究发现,我国一般通过以下两种方法进行降雨侵蚀力的估算。一种是直接对前人建立的估算模型进行引用,其中既有国外模型也有国内模型。如何兴元等[21]研究岷江上游土壤侵蚀动态时,引用了国外普遍适用的R因子模型。章文波等[14]的日雨量模型在我国引用率较高,截至2021年8月底,仅CNKI上的被引量就达 571次。在引用前人建立的模型时,缺少适用性验证的现象普遍存在,梳理的102篇文献中,这类文献占了约88%。因为模型建立过程中均使用的监测数据,除非应用的区域与模型建立的区域降水情况极度相似,否则直接引用很有可能导致误差。Xie等[22]的研究表明,章文波等建立的日雨量模型对站点侵蚀力真值存在一定高估,尤其对于侵蚀力较高的站点。另一种是利用已有资料建立适合当地的估算模型,再进行估算,采用这类方法的研究较少。如高克昌等[23]在重庆主城区,利用已有资料建立简易估算模型,通过与其他模型估算的值比较进行模型验证。戴海伦等[24]研究贵州省时,利用小区资料建立降雨侵蚀力简易模型,再计算站点降雨侵蚀力,但未对模型进行验证。在未来研究中,有必要加强模型的适用性研究,并对模型验证方法进行标准化;此外,对现有模型按照采用降雨数据类型、适用区域分门别类进行归纳也很有意义。
2 坡长坡度因子(LS)
2.1 标准定义及主要计算方法
在USLE中,地形因素对土壤侵蚀的影响由坡长坡度表示。在坡面或地块尺度,坡长坡度因子被定义为在降雨、土壤等其他条件都一致的情况下,某一坡长或坡度的坡面土壤侵蚀量与标准小区(坡长22.13 m、坡度5.14°或9%)土壤侵蚀量的比值,标准径流小区的坡长、坡度数值为1。CSLE中考虑到中国的大部分土壤流失来自陡坡,定义长20 m、宽5 m、坡度15°的小区为标准小区。
LS因子的原始定义和计算方法只适用于坡面尺度,其假设坡面的坡度具有均匀的梯度,任何不规则的斜率都必须被划分为更小的均匀梯度段。随着研究的深入,坡面侵蚀被划分为细沟侵蚀和细沟间侵蚀,Foster等[25]以此为根据提出坡长与细沟侵蚀量和细沟间侵蚀量比值的关系式。Mc Cool等[26]综合考虑了坡度和不同侵蚀类型侵蚀量比值对坡长指数的影响,提出的公式用于RUSLE。Foster和 Wischmeier开发了一种将不规则坡面划分为多个均匀段的方法,从而解释了坡面形状对土壤流失的影响,使得研究范围不再局限于坡面。然而,由于划分坡面难度很高,且用流域代替地块时坡长失去了预测地表水流和土壤侵蚀的意义[27]。故有学者建议用单位等高线长度的上坡排水面积替代坡长,即单位面积贡献法。该方法在研究复杂景观的土壤侵蚀有重要意义。但以上方法均忽略了水流路径和沉积的情况。LS因子计算结果的精度与DEM的分辨率以及研究区的地形起伏有较大关系。Wang等研究发现,在较大地形起伏区,相对于5 m分辨率,采用30 m分辨率估算的LS值普遍高估了20%以上,而在低地形起伏区低估了15%以上。在中等地势地区,这种偏差小于10%[28]。有学者研究指出土壤侵蚀量随着DEM分辨率的降低而降低。
我国学者根据实测数据,建立了坡长坡度的指数型计算公式(表1)。刘宝元等[29]在Mc Cool等公式的基础上,利用绥德、安塞和天水的观测资料,修正了RUSLE模型中10°以上坡地的坡度因子计算公式,该公式提高了10°以上坡地的坡度因子精度,并应用到CSLE中。刘斌涛等[30]在刘宝元算法的基础上,根据西南土石山区地形陡峭的特点细化了10°以上坡度的计算方法。
2.2 LS方程在中国的应用
基于对98篇流域或区域尺度土壤侵蚀或LS因子文献研究发现,80%的文献计算坡长坡度因子时,以栅格为单元提取 DEM得到坡长坡度,直接采用 USLE或修订的坡长坡度公式进行估算。但无论引用国外的计算公式还是国内的计算公式,都较少对公式的适用性进行验证,部分学者根据当地的地形条件选用缓坡或陡坡公式。在流域及以上尺度LS的计算中,坡长的定义和计算公式都与坡面尺度的存在差异,但只有20%左右的文献对坡长定义进行了修订。另外,还有学者对坡度划分等级后对地形因子直接赋值。在未来研究中,可加强高分辨率DEM的利用。有学者研究发现,高分辨率DEM的可用性已经超过了定义贡献区域流算法的方法研究。此外,还应加强坡长对径流和侵蚀的水文过程研究。

表1 中国坡长坡度计算公式
3 作物覆盖与管理因子(C)
3.1 标准定义及主要计算方法
C因子由特定的植被覆盖度、轮作顺序、管理措施的整体功能以及作物不同生长期降雨侵蚀力的分布决定。其定义为一定条件下有植被覆盖或实施田间管理的土地土壤流失总量与同等条件下的连续休闲地土壤流失总量的比值,无量纲,介于0~1之间,其值越大土壤侵蚀越严重。
USLE中先划分农作物生长期,再计算作物不同农作期作物小区与裸露小区的土壤流失比率,然后根据不同气候区降雨侵蚀力指数的季节分布加权平均求年平均C因子。我国学者通过该方法研究了东北[34]、西北[35]、西南[36]地区典型作物及不同管理措施下C因子值。在RUSLE中,对C值的计算采用次因子法,即在土壤流失率计算中考虑前期土地利用次因子(PLU)、冠层覆盖次因子(CC)、地面覆盖次因子(SC)、地表糙度次因子(SR)和土壤水分次因子(SM)等,每个因子都有相应的计算公式,并且不再划分生长期,以半月步长计算半月土壤流失率。但该方法需要大量的观测数据,在流域或区域尺度应用较为困难。随着GIS与RS的发展,通过构建C因子与植被因子之间的线性或非线性模型估算C因子成为主要的方法。用于C因子估计的植被因子包括植被覆盖度、植被指数和影像波段等[37]。除以上方法,利用前人的研究结果对土地利用图直接赋值也是常用方法之一。基于植被因子或者土地利用图估算C值忽略了管理因素,且一般使用遥感数据估计C因子值缺少与实测值的比较,可能对土壤侵蚀预测产生不确定性,但依旧有助于研究流域或区域土壤侵蚀潜力。
3.2 C因子方程在中国的应用
基于对105篇流域或区域尺度土壤侵蚀或C因子文献研究发现,我国学者估算C因子主要通过以下两种方法。一是直接使用已有的估算公式,这样的文献占了50%左右。众多学者利用蔡崇法公式在我国部分地区进行了C值的估算[38~40]。另外一种是根据研究区已有研究取得的C值直接进行赋值,这样的文献占了32%。但使用这两种方法估算的C值都未与当地的实测值进行验证。且林杰等[41]对蔡崇法公式进行实际应用时发现,只有植被盖度(fc)的值大于0.09时,代入公式C=0.6508~0.3436lgfc后C值才不大于1。C因子取决于降雨事件发生时植被和植被覆盖发展的特定阶段,也取决于之前的土地利用条件。例如,作物残茬、整地措施等,这些都会对土壤侵蚀产生不同的影响。因此,需加强系统的实地观测研究。
4 水土保持措施因子(P)
4.1 标准定义及主要计算方法
USLE方程中水土保持措施因子是指其他条件相同时,特定水土保持措施下的土壤流失量与未实施水土保持措施地块顺坡耕作时的土壤流失量之比。P值无量纲,典型的P值范围从反式梯田的0.2到没有水土保持措施的1.0,P值越大说明水土保持措施效果越差。与其他因子相比,P因子的定量化研究尚不充分。第一版USLE中,提供了等高耕作的P值;但研究人员考虑到小沟壑等情况,对P因子值进行了订正。在RUSLE中,P因子的计算采用保土措施的次因子法,增加了其他措施的因子值。上述两种计算方法在应用中有较大限制,前者仅适用于坡面尺度,后者需要详细的水土保持措施信息,包括不同措施的配置、单个措施的规模等,获取难度较大。
大量学者根据P因子的定义,基于径流小区的观测数据研究了不同水土保持措施的P值[9]。McCool等[26]认为,P因子的值是USLE/RUSLE因子中最不可靠的,指出在坡面给定坡度上观测到的数据有效性广泛降低。在流域或更大空间尺度上,通常基于GIS建模实现方程计算,但P因子的空间信息往往是缺乏的,使得在模型运算中忽略了水土保持措施对土壤侵蚀的影响。一些研究仅根据坡度计算P因子值。Wenner方法假设P因子与坡度之间存在线性关系[42]。林素兰等[43]通过对辽北低山丘陵区坡耕地11 a径流小区试验数据的对比研究,得出了P因子与坡度的关系式。但使用坡度计算的P因子值,缺少水土保持措施的信息;而且,在相同的坡度梯度下观察到P因子值具有高度可变性[6]。一些研究根据先前的研究工作得到的P值,按土地覆盖类别赋值[7]。但不同水土保持措施的效用受到气候、地形、土地利用等多种因素的影响,这可能会导致误差。此外,国际上有学者研究了P因子的替代指标,认为P因子的替代指标能够对P因子的值和可能带来的影响进行相对评估,这为我们国家P因子的研究提供了新的思路。
4.2 P因子方程在中国的应用
基于对103篇流域或区域尺度土壤侵蚀或P因子文献研究发现,78%的文献中P因子值都由直接赋值得出。花利忠等[44]根据研究区的实际情况,参照美国农业部手册进行P值的率定。部分学者直接参考相关研究资料对P因子赋值[45]。陆建忠等研究鄱阳湖流域土壤侵蚀变化时,从研究区的DEM中计算出百分比坡度,再将土地利用类型和坡度进行叠置分析,依据坡度和土地利用类型赋值[46]。少量研究通过经验公式直接计算P因子值,中国洛河流域[47]、延河流域[48]的土壤侵蚀评估时利用了林素兰等的公式。直接赋值法的估算精度受主观因素影响较大,经验公式得到的P值少有研究者对其进行验证。以上两种方法一定程度上忽略了因子随时间、管理等变化的情况。在未来研究中,应加强P因子定量化研究。并通过收集坡面的试验数据,建立P因子数据集,为定量化研究提供数据基础。
5 土壤可蚀性因子(K)
5.1 标准定义及主要计算方法
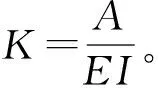
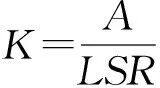
以上计算方法考虑的是长期的、平均的土壤对降雨的响应,忽略了土壤可蚀性的动态变化。冻融、风化、人类管理或踩踏土壤均会影响土壤的可蚀性。然而,现有模型实现土壤可蚀性的动态变化监测还有一定难度,为土壤侵蚀监测增加了不确定性和误差。
5.2 K因子方程在中国的应用
基于对105篇流域或区域尺度土壤侵蚀或K因子文献研究发现,K因子的估算方法主要有两种。一是直接引用国外的经验公式。有研究者通过实验室分析得到的土壤基础数据,直接引用国外的诺谟方程、EPIC模型等方法计算得到K值,这样的文献占了40%;二是基于第二次土壤普查数据或已有的土壤可蚀性资料,直接赋值,这样的文献同样占了40%。但高德武在黑龙江地区比较了实测值和诺谟法求得的值,发现将诺谟法求得的值加30%才可达到实测值水平[54]。张科利[53]、史学正等[55]研究表明,国外公式估算的K值与实测值之间差距较大。张科利等[56]研究中美农用地的K值发现,美国的土壤K值比中国大两到三倍。因此直接引用会造成误差,需要进一步修订才能表示我国的K值。在未来研究中,应加强土壤可蚀性因子的动态变化研究。
6 关于提高侵蚀模型评价质量的两个建议
综上,我国土壤流失方程各因子的研究程度存在明显差异。降雨侵蚀力因子有认可度较高的计算公式,但各公式的区域适用性研究较少,引用公式时也较少利用站点实测数据进行验证;坡长坡度因子计算方法较多,因子值的计算精度与DEM的分辨率有较大关系,同一计算方法和相同分辨率的DEM在不同地形起伏度的区域计算精度不同;作物覆盖与管理因子、水土保持措施因子缺乏完全反映因子影响因素的定量计算公式;土壤可蚀性因子的“标准值”缺乏统一的计算标准,目前的计算公式忽略了很多因素的影响。随着模型和遥感数据的发展,USLE/RUSLE不再仅用于坡面或地块尺度,在尺度上推过程中方程因子的计算方法可能产生不确定性,且计算的结果验证有一定困难。因为USLE/RUSLE估算的是总侵蚀率,而大部分监测得到的是净侵蚀率。由此,提出以下两点建议,促进我国土壤侵蚀评价模型的应用质量。
(1) 通过建设系统化、标准化的地面监测系统,观测和建立土壤侵蚀因子定量方法。根据我国地形地貌实际,综合考虑各类因素,建设系统化、标准化的地面监测系统,通过系列化标准小区监测结果,确定各个侵蚀因子的量化结果,或者通过与相对稳定的土壤参数结合建立估算模型,从而在全国推广应用。同时也可以通过适量的实际监测结果,修正常用的侵蚀因子计算模型,提高这些因子在中国的适宜性。
(2) 明确USLE和RUSLE的应用场景或边界,在与模型产生环境相差太大的环境下,不建议过分使用,从而确保模型的有限应用和高质量应用。如果在一些场合,超过了模型研发的边界条件,需要在结果中明确说明模型结果与实际应用场景的试验差异,为读者判断研究结果实际价值提供客观参考。
