再探2022年的中考数学文化试题*
2023-01-09江苏省徐州市第二十四中学221004
罗 伟 (江苏省徐州市第二十四中学 221004)
吕中学 (江苏师范大学数学与统计学院 221116)
《义务教育数学课程标准(2022年版)》(下称《课标2022》)指出,课程内容的选择要关注数学学科发展前沿与数学文化,继承和弘扬中华优秀传统文化[1]2.对于优秀的外国传统文化,也可以借鉴吸收.对于试题的命制,《课标2022》指出,可以设计合理的生活情境、数学情境和科学情境,适当引入数学文化[1]92.文[2]对2021年中考数学文化试题从基本数学思想、中国古代名著、经典成语故事、趣味数学拼图、著名文化遗产、国际数学视野进行了赏析,本文拟从数学史书、数学名人、数学游戏、数学应用、数学探索、数学交流等方面再探2022年各地中考数学文化试题.
1 数学史书
例1(株洲)中国元代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”.“方田一段,一角圆池占之.”意思是说:“一块正方形田地,在其一角有一个圆形的水池(其中圆与正方形一角的两边均相切,如图2所示).”问题:在此图中,正方形一条对角线AB与⊙O相交于点M,N(点N在点M的右上方),若AB的长度为10丈,⊙O的半径为2丈,则BN的长度为______丈.
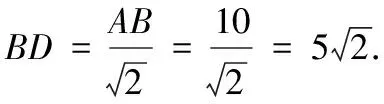
评析本题通过圆、正方形及相似三角形性质解决问题,难度中等,能培养学生几何直观能力.《四元玉鉴》是中国元代数学家朱世杰阐述多年研究成果的一部力著,全书共分3卷,24门,288问,书中所有问题都与求解方程(组)有关.《算学启蒙》也是朱世杰所著,内容由浅入深,循序渐进,自成系统,是一部很好的数学启蒙读物.随州卷考查了书中的追及问题,要求列一元一次方程.
在各地中考中还频频出现了一些其他的名著.
《周髀算经》是中国最古老的天文学和数学著作,约成书于公元前1世纪,在数学上的主要成就是介绍了勾股定理,湘潭卷考查了书中的弦图与三角函数;黄冈卷考查了勾股弦的规律及代数式表示.
《九章算术》是我国汉代的数学名著,在中考中出现的次数最多,多与方程(组)有关,宁波、眉山卷考查的是书中的二元一次方程组;武威卷考查一元一次方程;遵义卷考查“堑堵”的左视图;宜昌卷考查负数.
《孙子算经》是中国南北朝时期重要的数学著作,是一部最具智慧且激发人探寻数学奥妙的书,南充卷考查了书中著名的鸡兔同笼问题,但是要求列一元一次方程;岳阳卷考查百鹿进城,实际上列一元一次方程容易求解.《数书九章》由南宋数学家秦九韶所著.全书采用问题集的形式,共列算题81问,分为9类.宜宾卷考查了书中根据公式由三边求三角形的面积.
《算法统宗》是由明代数学家程大位编著的一部应用数学书,该书曾传入日本、朝鲜、东南亚和欧洲,成为东方古代数学的名著.成都卷考查了书中列二元一次方程组.《御制数理精蕴》于清康熙年间编著而成,是一部介绍包括西方数学知识在内的数学百科全书.毕节、达州卷考查了书中列二元一次方程组.武威卷还考查了清末教科书《最新中学教科书用器画》中的尺规作图、计算及证明问题.
数学史书是数学的瑰宝,反映了古代数学家及劳动人民的智慧,对现在的学生及教师来说,仍有很大的学习价值,我们仍要汲取其中营养,以丰富自己的人文底蕴.
2 数学名人
例2(大庆)函数y=[x]叫做高斯函数,其中x为任意实数,[x]表示不超过x的最大整数.定义{x}=x-[x],则下列说法正确的个数为( ).
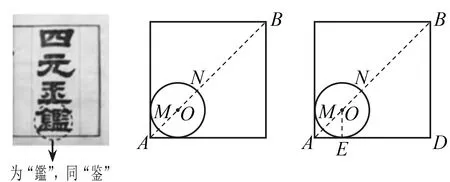
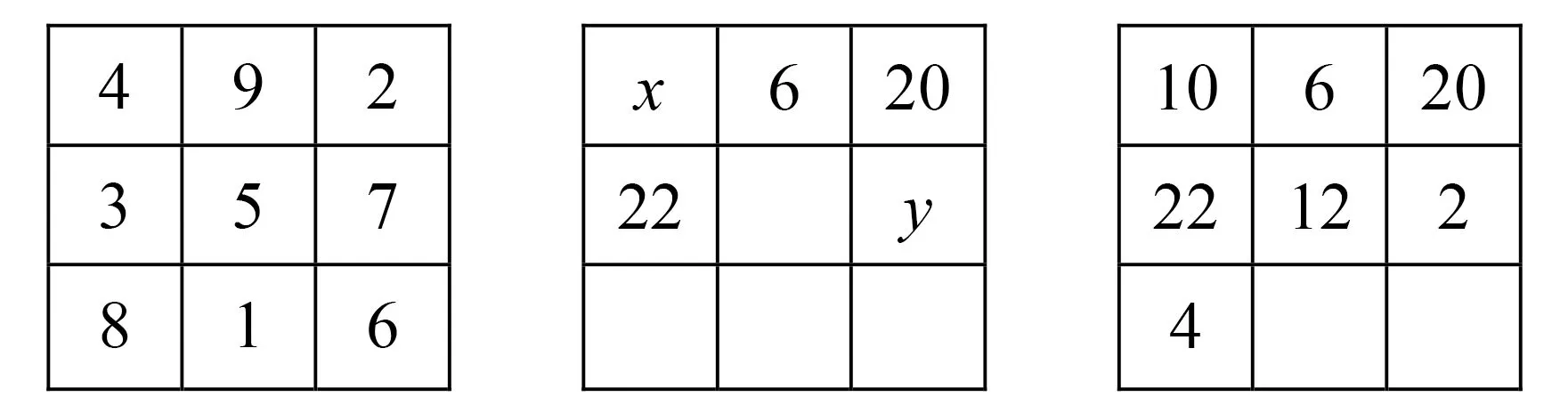
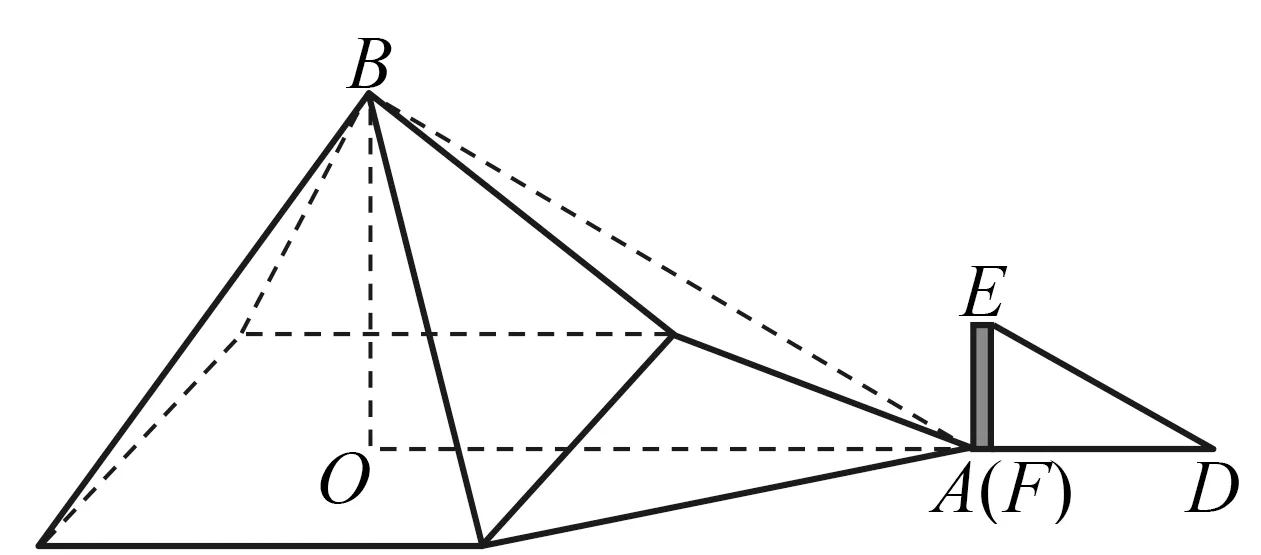
①[-4.1]=-4;② {3.5}=0.5;③高斯函数y=[x]中,当y=-3时,x的取值范围是-3≤x<-2;④函数y={x}中,当2.5 A.0 B.1 C.2 D.3 解根据高斯函数的定义,[-4.1]表示不超过-4.1的最大整数,结果为-5,①错误;{3.5}=3.5-[3.5]=3.5-3=0.5,②正确;当-3≤x<-2时,y=[x]=-3,③正确;y={x}=x-[x],当x=2.5时,y=2.5-[2.5]=2.5-2=0.5,当x=3.5时,y=0.5,当x=3时,y=3-[3]=3-3=0,当x从2越来越大,不断接近于3时,此时y接近于1,④正确,故选D. 评析函数y=[x]称为取整函数,也称高斯函数,它的图象很美,成周期分布.本题能培养学生的符号意识,做到用数学的眼光观察现实世界.高斯是德国著名数学家、物理学家、天文学家、几何学家、大地测量学家,是世界上最重要的数学家之一,享有“数学王子”的美誉. 例3(泸州)菲尔兹奖是国际上享有崇高声誉的一个数学奖项,每四年评选一次,主要授予年轻的数学家.下面数据是部分获奖者获奖时的年龄(单位:岁):29,32,33,35,35,40,这组数据的众数和中位数分别是( ). A.35,35 B.34,33 C.34,35 D.35,34 评析 一方面,这个题目难度不大,能培养学生的数据观念,另一方面从题目中我们看出年轻数学家取得卓越的成果,让我们钦佩.菲尔兹奖,是加拿大数学家菲尔兹倡议设立的国际性数学奖项,于1936年首次颁发.菲尔兹奖是数学领域的国际最高奖项之一.因诺贝尔奖未设置数学奖,故该奖被誉为“数学界的诺贝尔奖”. 数学名人一般指著名的中外数学家,他们解决了数学难题,对数学的发展与传播作出了巨大的贡献.高斯和菲尔兹是外国数学家的代表,中国也有数学家为世人所敬仰,比如程大位和华罗庚等.以数学家为背景命题,能使学生确立学习榜样,树立远大理想,激发学习热情. 例4(武汉)幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及每条对角线上的3个数之和相等,例如图4就是一个幻方.图5是一个未完成的幻方,则x与y的和是( ). 图1 图2 图3 图4 图5 图6 A.9 B.10 C.11 D.12 解幻方的特点是每一横行、每一竖列以及每条对角线上的3个数之和相等,此外,还有一个特点,最中间一个数是包含这个数的每一行、每一列、每条对角线三个数的平均数.包含x的第一行、第一列三个数的和相等,可得第一列最下面一个数是6+20-22=4,4和20的平均数为12,所以最中间一个数是12.对角线上这三个数的和为12×3=36,所以x=36-4-22=10,y=36-22-12=2,x+y=10+2=12,如图6所示. 评析图4中只知道三个数,根据九宫格的本质就可以求出剩下的六个数,实际上是运用方程的思想.九宫格(或者叫三阶幻方)也可以看做数学游戏,在规则下,能培养学生的代数推理能力、模型思想,培养用数学的语言表达现实世界的能力.另外威海卷也考查了三阶幻方;江西卷考查了七巧板拼图及相关的计算. 数学游戏比纯粹的数学有趣,学生都喜欢也更易入手.因此数学游戏可以辅助数学学习.在游戏的过程中,如果走不下去,可以请同学互相帮助,进行点拨,这一过程能培养思维与能力,达到寓教于乐的效果,做到学会学习. 例5(广西北部湾)古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔的影子顶部直立一根木杆,借助太阳光测金字塔的高度.如图7,木杆EF长 2 m,它的影长FD是4 m,同一时刻测得OA是268 m,则金字塔的高度BO是m. 图7 评析我们知道,直接测量金字塔的高度不好办,数学家泰勒斯利用立杆测影的方法通过列比例式巧妙地解决了这个问题.此外,娄底卷的结绳计数也体现了古代劳动人民的智慧,能培养学生的数学应用意识. 数学应用,就是在生活中通过数学知识去解决实际问题,显示了数学的实用价值.对于人们来说,能解决问题才是目的,这也说明了数学是解决实际问题的有效工具,能培养实践创新素养. 例6(德阳)古希腊的毕达哥拉斯学派对整数进行了深入的研究,尤其注意形与数的关系,“多边形数”也称为“形数”,就是形与数的结合物.用点排成的图形如图所示. 其中,图8的点数叫做三角形数,从上至下第一个三角形数是1,第二个三角形数是1+2=3,第三个三角形数是1+2+3=6……图9的点数叫做正方形数,从上至下第一个正方形数是1,第二个正方形数是1+3=4,第三个正方形数是1+ 3+5=9……由此类推,图11中第五个六边形数是. 图8 图9 图10 图11 解我们仔细看题,结合图形寻找规律.图11的点数叫做六边形数,从上至下第一个六边形数是1,第二个六边形数是1+5=6,第三个六边形数是1+5+9=15,第四个六边形数是1+5+ 9+13=28,第五个六边形数是1+5+9+13+ 17=45,故答案为45. 评析毕达哥拉斯学派对整数的研究比较深入,本题的思路就是数形结合的思想,结合图8~10告诉的结论去寻求规律,最后得出结论. 例7(遂宁)“勾股树”是以正方形一边为斜边向外作直角三角形,再以该直角三角形的两条直角边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一颗树而得名.假设如图12所示分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理,第六代勾股树中正方形的个数为. 图12 解第一代勾股树中正方形的个数是1+2+3(或20+21=3),第二代勾股树中正方形的个数是1+2+4=7(或20+21+22=7),第三代勾股树中正方形的个数是1+2+4+8=15(或20+21+22+23=15),猜测第六代勾股树中正方形的个数是1+2+4+8+16+32+64=127(或20+21+22+23+24+25+26=127),故答案为127. 评析通过观察、总结、归纳,可以看出规律,真没想到,勾股树中还有如此美妙的算式.不论是数学家还是教师、学生,都需要数学探索,用数学的思维思考现实世界,过程虽然艰辛,但在追求真理的过程中能感受到数学的力量以及成功后的喜悦感,增强了科学精神. 例8(遵义)图13是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图14所示的四边形OABC.若AB=BC=1,∠AOB=30°,则点B到OC的距离为( ). 图13 图14 图15 评析这个会徽展示的就是勾股定理的连续应用,得到了美丽的图案.在教材中,就是通过此方法不断产生无理数.国际数学教育大会(ICME)正是数学家交流数学成果的会议,大家通过交流,能了解数学的最新成果,互相学习,增进友谊,为攀登数学高峰共同努力. 例9(遂宁)图16中既是轴对称图形又是中心对称图形的是( ). 图16 A.科克曲线 B.笛卡尔心形线 C.阿基米德螺旋线 D.赵爽弦图 解轴对称图形是一个图形沿着一条直线折叠,两旁的部分能完全重合,中心对称图形是一个图形绕着一个点旋转180°,与原来的图形能完全重合,本题选A. 评析轴对称图形和中心对称图形的判断属于基本技能,难度不大,我们还要了解题目中三线一图,科克曲线是一种典型的分形曲线,它是瑞典数学家科克于1904年构造出来的;笛卡尔心形线传说是瑞典的小公主根据法国著名的数学家笛卡尔给她写的信中的一个公式r=a(1-sinθ),画出的图形像心形而得名;阿基米德是古希腊数学家,阿基米德螺旋线是一个点匀速离开一个固定点的同时又以固定的角速度绕该固定点转动而产生的轨迹;三国时期吴国的数学家赵爽为《周髀算经》一书作序时创制了一幅图,以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成,被称为赵爽弦图,它经典而久远,被誉为“中国数学界的图腾”.本题中的四个图形三曲一直背景深厚,数形结合,数学味浓,说明中外数学家的积极贡献得到了国际认同,促进了人类的文明与繁荣. 数学交流不仅是中外交流、古今交流,也可以是师生交流,通过交流,我们去分享、聆听和讨论数学的思想、方法,感受、学习数学中的文化,丰富自己的底蕴,培养责任担当. 通过对2022年的中考数学文化试题分析可以看到,数学史书能开阔视野,数学名人树榜样力量,数学游戏能激发兴趣,数学应用显实用价值,数学探索呈艰辛之路,数学交流促专业成长.在以后的教学中,根据陶行知先生“做中学”的教育思想,教师可以适时开展数学文化讲座,让学生多阅读与赏析数学文化相关书籍,参加数学文化实践活动、数学文化知识竞赛、绘制数学文化手抄报等,不断提高数学文化素养.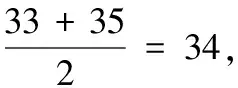
3 数学游戏
4 数学应用

5 数学探索


6 数学交流

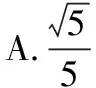



7 结语
