天然气水合物饱和度测井解释模型及方程

李宁，孙文杰，李心童，冯周，武宏亮，王克文

（1. 中国石油勘探开发研究院，北京 100083；2. 北京大学，北京 100871）

0 引言

天然气水合物又称“可燃冰”，是由天然气和水分子在高压低温环境下形成的冰态、结晶状、超分子笼形化合物，主要赋存于大陆永久冻土区、极地地区以及水深大于300 m的海域沉积层[1-3]。水合物分布范围广、资源量巨大、燃烧清洁，被认为是最具开发前景的非常规能源。全球已探明水合物资源总量换算成甲烷气体为（1.8～2.1）×1016m3[1-5]。据测算，中国海域亦具有非常广阔的水合物勘探前景，南海11个潜在水合物赋存区域的资源量保守估计约为680×108t[2]。

水合物储集层具有埋深浅、未成岩、胶结性差的特点，由于其赋存形式复杂，定量评价和安全开采两方面都面临巨大挑战。近些年中国在水合物实验模拟、地球物理探测研究以及开发技术等方面均取得快速发展。青岛海洋地质研究所水合物实验室、中科院广州能源所水合物研究中心建立了水合物地球物理模拟实验装置，较早开展了含水合物沉积物的声学特性及水合物饱和度研究[6-10]。中国海洋石油周守为院士团队研究了南海深水天然气水合物的赋存状态及成藏特点，原创发明了全新的固态流化水合物开采方法[3]，在海底天然气水合物试采方面取得重要突破。

作为重要的地球物理勘探技术之一，测井无疑是定性识别和定量评价水合物储集层的有效手段，国内外许多学者近年来先后对水合物测井解释评价进行了研究探索。Collett等、Tanahashi等研究了水合物在电阻率、声波、自然伽马等测井曲线上的响应特征[11-12]。田贵发等通过对祁连山冻土区水合物科学试验孔的测井资料研究，建立了富冰型、煤层自生自储型、孔隙型、层理型等多种水合物储集模式测井曲线典型特征图[13]。王秀娟等根据电阻率测井利用阿尔奇（Archie）公式计算了神狐海域SH2站位的水合物饱和度，并讨论了电性参数 a、m及 n取不同数值时饱和度的计算误差[14]。Hesse R等、Schulz等提出了利用氯离子质量浓度异常识别水合物储集层、计算水合物饱和度的方法[15-16]。Lee等利用阿拉斯加北部陆坡水合物测井及岩心资料，开展了利用核磁共振、电阻率及地层水盐度等进行水合物饱和度计算的方法研究，并比较了不同方法饱和度计算结果的差异[17]。莫修文等进一步发展了基于氯离子浓度的水合物饱和度计算方法，提出了首先利用Archie公式计算视地层水电阻率，然后利用视地层水电阻率反算地层水氯离子质量浓度，最后根据氯离子浓度计算水合物饱和度的方法[18]。马龙等用数字岩心技术模拟研究了水合物饱和度模型参数的变化规律[19]。陈玉凤等利用广州能源研究所自主设计的水合物合成及电阻率测量系统，通过实验研究了水合物的电学特性，发现水合物沉积物饱和度实验结果呈明显非阿尔奇现象[20]。陈玉凤等进一步利用分形孔隙模型通过数值模拟研究了含天然气水合物沉积物的电阻率特性[21]。唐叶叶选取祁连山冻土区岩石样品和人造岩心，在水合物合成实验基础之上进行了电阻率特性研究。林霖、赵军等探讨了利用声波数据计算天然气饱和度的可靠性[22-23]。Yang等在水合物饱和度定量计算中也采用了相同的方法[24]。Xie等结合核磁共振资料分析了不同孔隙中天然气水合物的形成模式，并选用印度尼西亚公式定量计算水合物饱和度[25]。

分析目前国内外水合物饱和度研究现状，得出 2点认识：①虽然形成了基于氯离子浓度、电阻率及核磁测井等不同的水合物饱和度计算方法，但基于电阻率测井曲线的水合物饱和度评价还是最为基础和应用最多的核心方法；②岩心实验、数值模拟及理论分析均表明，由于水合物在储集层中赋存状态、空间分布的复杂性，其电性特征在多数情况下呈现显著的非Archie特性。因此，充分考虑水合物的非Archie特征，确定更加精确的饱和度计算模型和参数，是提高水合物饱和度测井评价精度的关键。

作者研究团队早在15年前就开展了水合物饱和度测井评价方法的研究，相关研究结果“一种测定天然气水合物储层饱和度的方法及设备”获得了国家发明专利授权（ZL201310512178.X）。同时，本文第1作者在2013年美国石油地质学家协会（AAPG）“细颗粒沉积系统及非常规资源”国际学术研讨会上作了题为“水合物饱和度模型确定及测井定量评价新方法”的报告，并将研究结果以摘要形式发布[26]。为使提出的理论方法更加完善，笔者从水合物储集层导电机理、实验数据分析及解释评价方法等方面又做了进一步深入研究。研究结果不仅给出了适合各类不同赋存方式水合物饱和度的定量评价方法，有效提高了测井解释精度和对水合物储量规模的预测精度；而且通过新公式和Archie等传统公式计算结果的差异分析，可以准确判别水合物的赋存状态，为后期水合物开发方式的确定提供了测井分析依据。

1 实验及数据分析

众所周知，含油气饱和度即油气占孔隙体积的百分比，直接决定油气储量规模，是测井评价的核心参数之一。对于一般沉积岩（碎屑岩、碳酸盐岩和页岩）和岩浆岩（火山岩、火成岩）油气层，确定饱和度的实验过程是：岩心被完全饱和地层水后加压用油气驱替，电阻增大率随油气饱和度增加而增大。实际解释评价饱和度是其反过程，即依据测井得到的地层电阻增大率来计算饱和度。当水合物存在于固结成型的砂岩地层孔隙中时，水合物饱和度即水合物占孔隙体积的百分比，与常规油气饱和度一致。但大多数情况下，尤其在海底地层沉积中形成的水合物一般具有埋深浅、未成岩、胶结性差的特点，并以分散状、层状等多种形态赋存。通过对现场取得的水合物样品进行分析，可以初步判定水合物在储集层中的分布与常规油气有很大不同，主要差异是油气完全赋存在地层岩石孔隙当中，但水合物却可以堆积形成地层的“岩石骨架”。

研究水合物饱和度的最大难点是水合物样品在地面会迅速气化分解，无法用传统的驱替法确定电阻增大率与水合物饱和度之间的实验关系。十余年来，不少学者[10-11,20]先后提出新的实验思路，设计出能够模拟低温高压环境下水合物生成及电阻率变化的测量装置。上述装置一般由反应系统、温度控制系统、压力控制系统和测量系统等构成（见图1）。反应系统主体为高压容器，内置沉积物样品；温度控制系统用于提供水合物实验所需的温度环境；压力控制系统维持反应系统的压力恒定，由压力泵、压力表及安全阀等部件组成；测量系统实时采集含水合物岩样的电阻率及温度、压力等参数，含控制电脑、数字电桥、温压传感器等主要部件。利用此类装置可以测量水合物不同生长阶段的电阻率变化，从而得到不同水合物饱和度下的电阻增大率值。这类装置的意义还在于可清晰地观察到水合物的生成规律、在储集层中的分布形式及其导致的电阻率由小增大的变化过程。

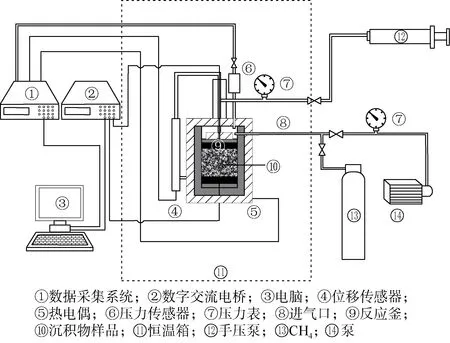
图1 模拟低温高压环境下水合物生成及电阻率测量装置

依据取心观察和相关实验结果的分析发现，不同饱和度情况下水合物在地层中的分布状态如图2所示：①当水合物开始在地层中形成时，由于其饱和度较小，此时水合物像常规油气一样呈分散状充填在孔隙空间中（见图2a）；②随着水合物的不断生成，其饱和度逐渐增大，开始在某些部位以颗粒的形式形成支撑骨架（见图2b）；③当水合物充分生成、饱和度增大到一定程度后，水合物会单独堆积成层，变成地层骨架的一部分，与骨架颗粒一起承担上覆压力（见图2c）。需要特别说明的是，鉴于水合物是固态烃，当它以支撑骨架的颗粒状或成层状存在时，它的体积可等同于相同大小的孔隙体积，因此饱和度的定义依然是水合物在孔隙体积中所占的百分比。当水合物饱和度由小增大时，其电阻率测量值变化的实验规律一般如图3所示，即在双对数坐标下随着水合物饱和度增高呈单调递增形态。为了和传统的表示方法一致，图 3横坐标仍采用含水饱和度Sw，它与水合物饱和度Sho的关系是Sho=1-Sw。

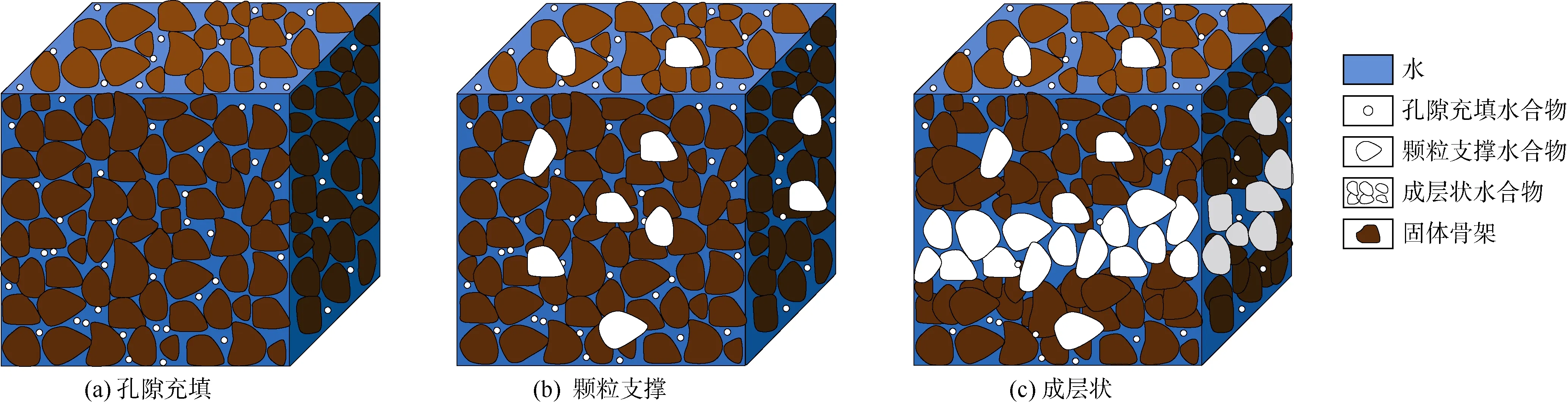
图2 不同饱和度情况下水合物在地层中的分布状态

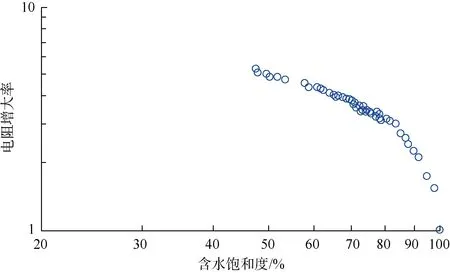
图3 水合物饱和度-电阻增大率实验关系

2 饱和度模型及其物理意义

2.1 饱和度方程的推导

1989年，本文第 1作者首次提出了非均匀各向异性测井解释体积模型[27]（见图4），并据此推导出电阻增大率-含油（气）饱和度的一般形式（见式1）：

图4 非均匀各向异性测井解释体积模型

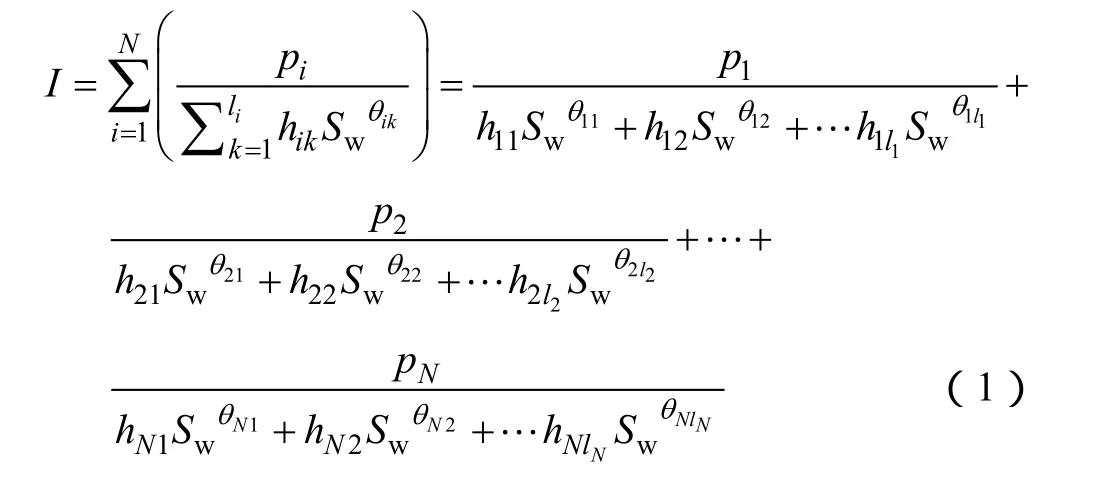
常规砂岩及非均质缝洞储集层饱和度模型均是上述一般形式的特例[28]。

为便于理解，可将上述一般形式视为电阻增大率与含油（气）饱和度的广义“通解方程”，其不同的截短方式可视为“通解方程”的各个“特解”：

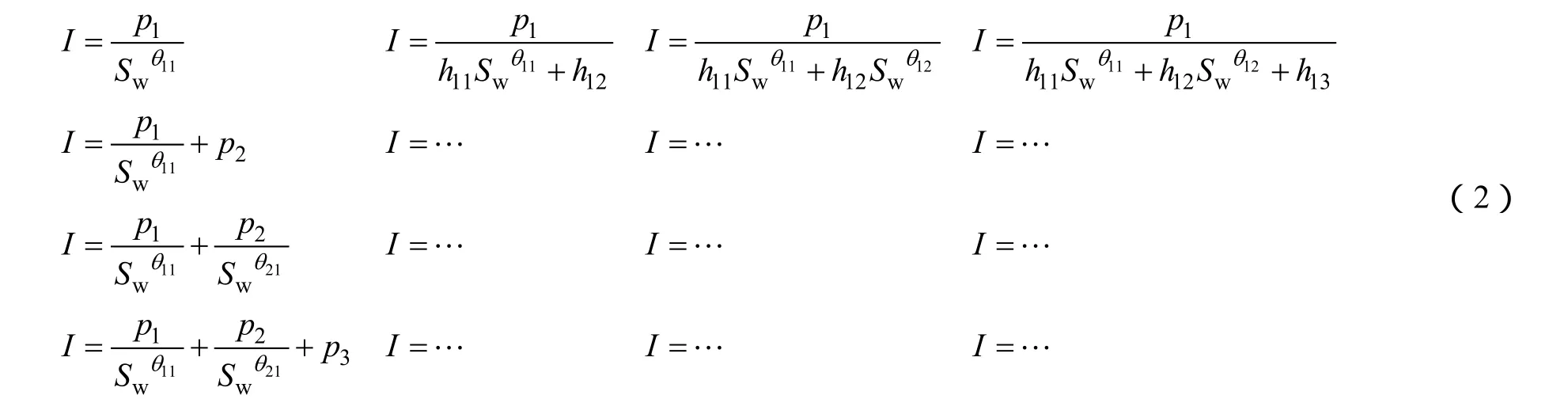
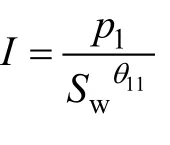
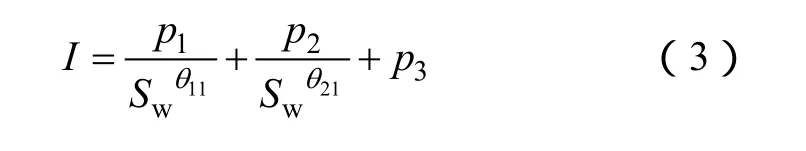
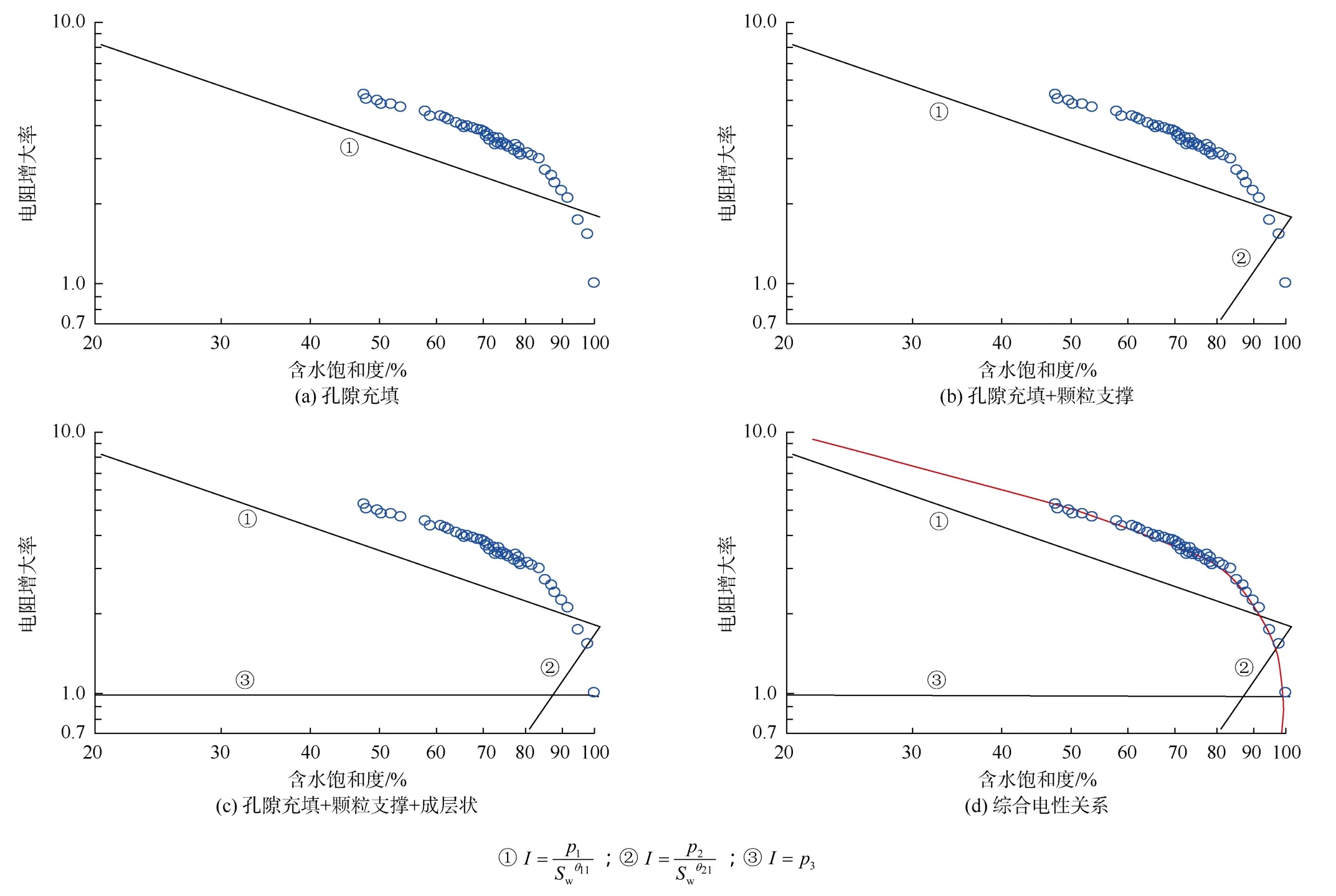
图5 不同赋存状态水合物饱和度与电阻增大率关系

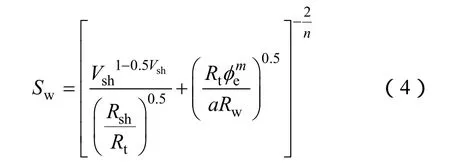
该方程式涵盖了常见水合物赋存形态，可作为用电阻增大率计算水合物饱和度的基本方程。Xie等在水合物饱和度定量计算中采用了以下公式：

此式又可以转化为：

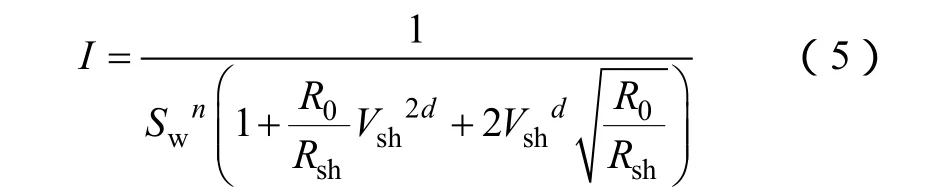
显然这就是Poupon等提出的印度尼西亚公式。

对比前文给出的电阻增大率-含油（气）饱和度一般形式的几种不同截短形式，可以看出式（5）为一般形式右侧分母中取两项的结果，即印度尼西亚公式是一般形式在泥质含量较高时饱和度方程的特例。

2.2 方程（3）的物理意义

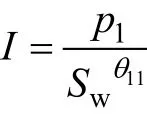
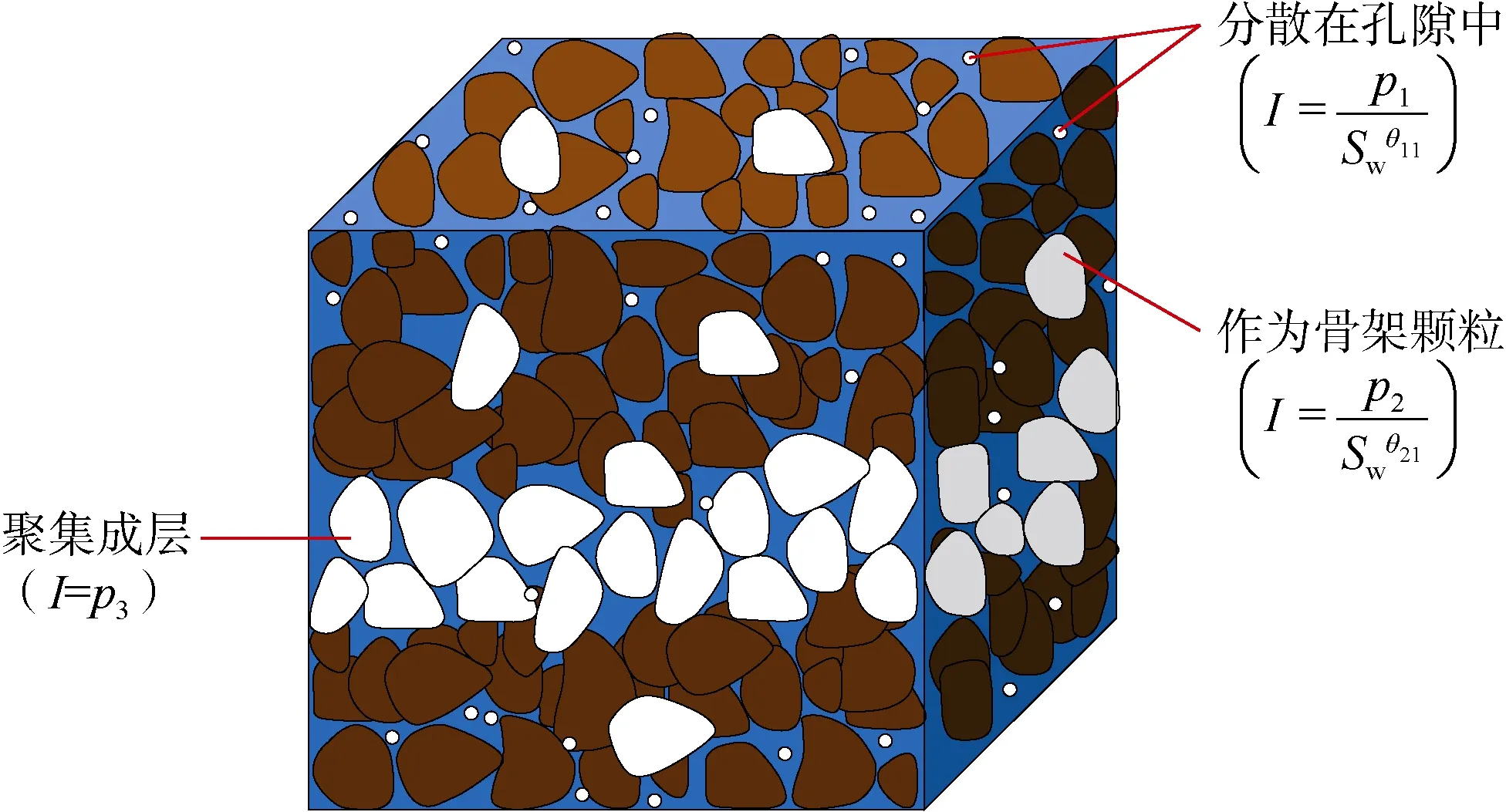
图6 方程（3）的物理意义

水合物储集层类型的精确评价对其高效开发具有重要意义。依据典型的天然气水合物储集层的分类[6]（见图 7），结合本文给出的水合物饱和度计算方程（3），可以用测井方法有效识别水合物沉积储集层的类型，具体分为4种情况：①如果方程（3）中仅保Archie项，就能准确计算水合物饱和度，则此水合物储集层类型应该是“极地砂岩储集层”或“海洋砂岩储集层”；②如果方程（3）中仅保留第3项，就能准确计算水合物饱和度，则此水合物储集层类型应该是“脉状块状水合物”储集层；③如果方程（3）中必须同时用到前两项，才能准确计算水合物饱和度，则此水合物储集层类型应该是“海洋非砂岩储集层”；④如果方程（3）中 3项都必须采用，才能准确计算水合物饱和度，则此水合物储集层类型应该是“细粒沉积物储集层”。

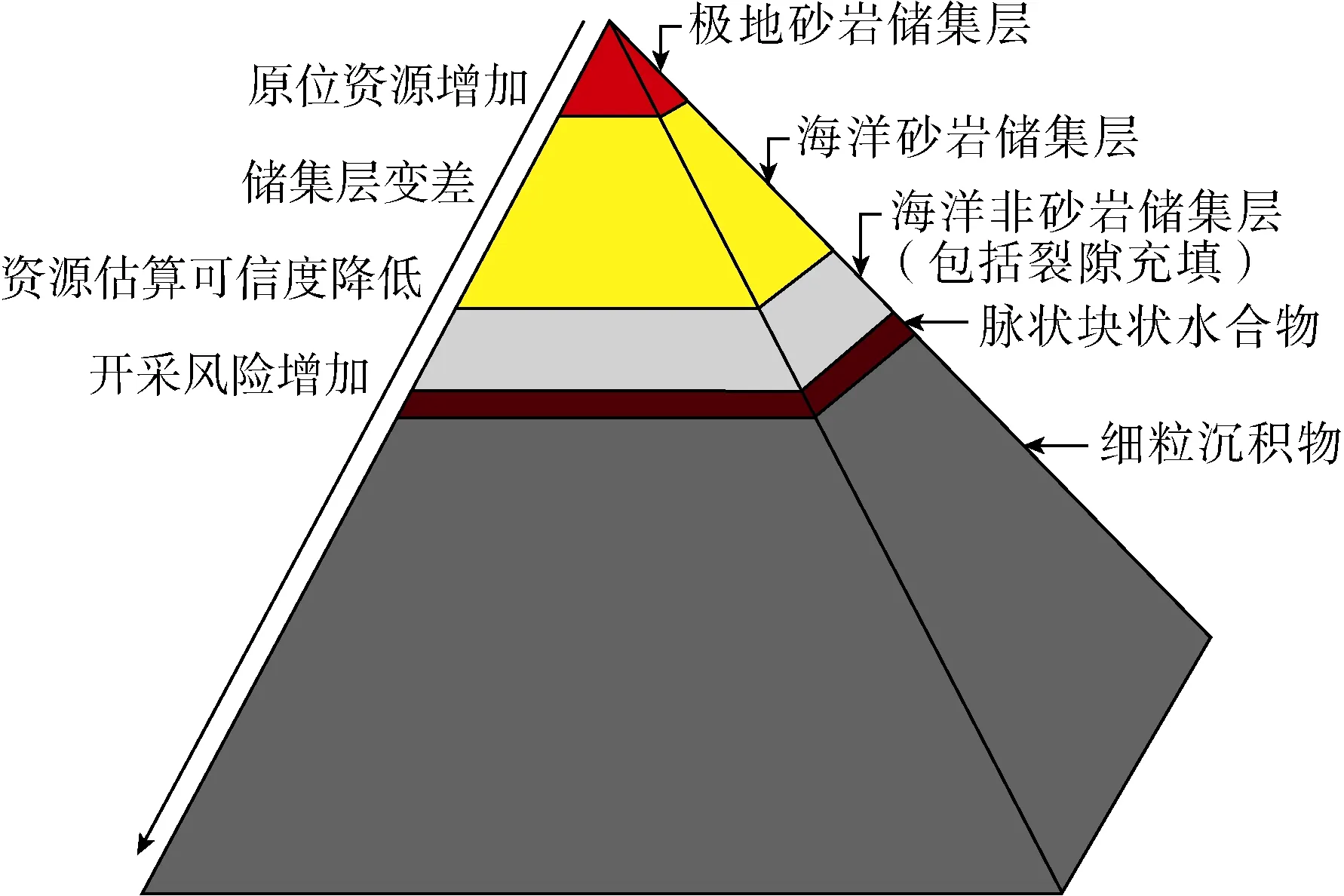
图7 天然气水合物储集层分类

3 应用实例

图 8是南海某井水合物样品实测饱和度和测井计算饱和度结果的对比。图中自左向右第 1道为井眼情况；第2道为井径曲线和自然伽马曲线；第3道是深度；第4道是电阻率曲线；第5道是三孔隙度曲线；第 6道为孔隙度计算结果和岩心分析孔隙度的对比；第7道是传统Archie公式处理得到的地层水合物饱和度、本文方程（3）计算得到的地层水合物饱和度以及与取心测试结果的对比曲线；第8道显示了传统Archie公式处理得到的地层水合物饱和度与本文方程（3）计算得到的地层水合物饱和度的差异。图中各道中横线和圆点符号表示相应的取心测试分析结果。

图8 南海某井水合物饱和度测井计算结果与取心测试结果对比

研究表明，水合物储集层段（300～325 m井段）与正常地层测井响应具有显著差异，随着水合物含量的逐渐增加，地层电阻率逐渐升高，同时由于固态水合物逐渐替代原含水孔隙部分，地层声波速度增大，声波时差值明显降低。从不同方法饱和度计算对比结果可以看到，传统Archie模型处理得到的水合物饱和度值偏低，本文方法处理得到的水合物饱和度与取心测试结果更为吻合，两者计算水合物饱和度相差约10%。通过对比主要深度点的Archie模型饱和度计算结果、最优饱和度模型计算结果及取心测试饱和度分析结果可知，优化模型计算的饱和度数值分布在取心测试饱和度的两侧，相对误差约为10%，而Archie模型计算的饱和度数值均小于取心测试分析的饱和度，相对误差约为45%。

按储集层有效厚度20 m、孔隙度50%计算，假设水合物有利勘探面积为 10 km2，饱和度相差 10%时对应10×106m3水合物储量，饱和度计算结果的可靠性将对整个区域水合物资源评价及开发方案设计产生重要的影响。

4 结论

电阻率-含油（气）饱和度关系一般形式不仅适用于常规含油气储集层，同样适用于天然气水合物饱和度定量计算。

对天然气水合物储集层，一般形式中保留 3项即可满足饱和度准确评价的需要，其物理意义分别对应了水合物颗粒完全分布于地层岩石孔隙中、以颗粒方式支撑和以成层状3种状态存在时的电阻增大率。

针对海洋水合物沉积储集层分类，当方程（3）中仅保留第1项（即Archie公式）时，可用于“极地砂岩”或“海洋砂岩”两类天然气水合物储集层饱和度定量计算；仅保留第3项时，可用于“脉状块状水合物”储集层；同时保留前两项时，可用于“海洋非砂岩”储集层；3项同时保留时，则可用于“细粒沉积物”储集层。这一规律亦可反过来判断天然气水合物储集层类型。

致谢：吉林大学莫修文教授提供了水合物储集层相关研究资料，在此表示感谢！

符号注释：

I——电阻增大率，无因次；N——储集层岩石等价的串连薄片数；li——第i个薄片导电介质总数；k——导电介质编号；Sho——水合物饱和度，f；Sw——含水饱和度，f；pi——待定参数；hik——待定参数；θik——待定参数；Vsh——黏土体积，f；Rsh——泥岩电阻率，Ω·m；Rt——地层电阻率，Ω·m；Rw——地层水电阻率，Ω·m；R0——地层完全含水时的电阻率，Ω·m；Φe——有效孔隙度，f；a——岩性系数，无因次；m——胶结指数，无因次；n——饱和度指数，无因次；d——常数。