基于钻进模拟系统的岩层结构振动反馈信息试验研究
2023-01-09张宏伟
张宏伟
(1.中国中煤能源集团有限公司,北京 100120;2.中煤陕西榆林化工能源有限公司,陕西 榆林 719054)
针对煤矿顶板事故的致灾机理和预防控制方法,国内外学者从采矿、煤田地质、工程地质、工程力学等学科的不同视角,对顶板灾害活动特征及其力学机制、顶板支护结构失稳的灾变与预报分析、预报系统等方面进行了大量探索[1-4]。顶板岩性结构探测的设备开发与数据处理技术不断提升,在研究钻进信号参数响应规律方面取得了极大进步,在岩层识别方面进行了大量的分析,总结了丰富的科研经验,但仍存在着一定的问题:①只考虑单一参数来分析岩层结构及厚度分布,还需要提高精确度,将多种参数与岩石结构特性进行互补与融合分析;②大部分钻探设备庞大,价格高昂,二次开发费用高;③大部分研究均是在数值模拟的基础上进行试验,实际试验时各参数在钻进不同岩石情况下,钻进反馈参数均会发生改变,缺乏在试验室内钻进信号采集分析的成套设备[5-8]。
基于上述问题,团队设计研发了多参数多角度识别顶板隐患的钻进模拟系统,实现了钻进模拟实验的自动化、集成化。钻机机身将推力、位移、扭矩、转速、三轴振动传感器等多个高精度传感器集合于一体,有效解决了单一传感器采集数据不全面的问题,将多传感器信息进行互补融合,分析钻进参数的响应特征[9,10]。自动化测控系统和高频率采集卡保证了数据精确度,同时也提高了钻进过程实时信息的获取、处理及传输技术。开发了一种新型岩石钻进测试系统,建立相似模拟试验台,制作试件简单方便,可进行不同种类岩石试样在多种钻机参数(钻杆推力、钻进速度、推进距离、转速、扭矩、X、Y、Z 三轴振动信号)组合模式下的钻进测试,钻探测试的同时并实时反馈岩层结构的变化。
1 钻进模拟系统
1.1 钻进设备
煤炭生产中面临的主要问题是安全生产问题,顶板事故的累计死亡人数和发生频率都高居首位。大量煤炭企业林立与开采资源需求的增加,使煤炭企业在开采时增加了掘进巷道速度与掘进工程量,并且逐渐向深部的煤炭资源转移,虽然企业加强了安全生产管理,但随着基础工程数量的增多顶板事故仍威胁着矿井的安全生产[11-14]。针对顶板安全隐患问题,为加强灾害预防与治理能力,设计研发了多参数多角度智能识别顶板隐患的钻进设备,主要由多工位试验台、高压加载试验台、钻进系统、测控系统和配套泵站五部分组成,如图1所示。

图1 钻进设备组成结构
该钻进设备实现了智能化、自动化、集成化的目标,钻机机身将推力、位移、扭矩、转速、三轴振动传感器等多个高精度传感器集合于一体,有效解决了单一传感器采集数据不全面的问题。
1.2 系统功能
钻探试验实际由两部分组成,分别是钻孔设备与探测介质,当向巷道顶板钻进锚杆锚固孔时所遇到的岩石种类多种多样,因此了解岩石的组成和构造十分重要。钻探试验以模拟不同强度的岩石为探测介质,研究影响钻孔破岩效率的主要因素和试验设备的破岩做功分析,将采集的钻进参数进行处理达到识别岩层强度变化的目的[15-18]。
多参数多角度智能识别顶板隐患的钻进设备可以将多传感器信息进行互补融合,分析岩石性质与钻进参数的响应规律;自动化测控系统和高频率采集卡保证了数据精确度,同时也提高了钻进过程实时信息的获取、处理及传输技术;研究了钻孔破岩过程中的主要影响因素,基于能量守恒理论分析了钻进过程中的能量损耗问题,推导出岩石的单位体积破碎比功值,以岩石的抗压强度作为识别参数进行拟合,开发了一种新型岩石钻进测试系统,建立相似模拟试验台,可进行不同种类岩石试样在多种参数组合控制模式下的钻进测试,根据测量后的拟合结果判断岩层厚度与软弱岩层位置[19,20]。
2 试验方案
利用随钻探测设备进行试验,试验材料选择抗压强度差异显著的青砖、红砖、青石、花岗岩。设计两次试验方案,首先选用青砖与红砖进行初次试验,再进行青石与花岗岩试验,改变不同力学参数观察效果。
2.1 青砖与红砖试验方案
选用工业规格强度等级为MU15的青砖和MU30的红砖。根据国家标准的烧结普通砖规定,青砖的平均抗压强度为15MPa,红砖的平均抗压强度为30MPa。通过电机分配的液压系统流量控制钻进设备的转速和推力的初始值。具体流程如下:
1)方案一:选取青砖材料,堆积高度38cm左右,四周加固,调整液压系统流量控制初始值推力与转速值,进行第一次钻孔试验,采集推力、推进位移、转速、扭矩、振动等参数。
2)方案二:选取红砖材料,堆积高度38cm左右,同种钻进条件下,采集推力、推进位移、转速、扭矩、振动等参数变化。
3)方案三:改变推力初始值,进行组合岩层试验,保证试验条件相同,红砖堆积高度为38cm,布置在下,青砖堆积高度为38cm。
4)方案四:再次改变推力初始值,进行组合岩层试验保证试验条件相同,红砖堆积高度为38cm,布置在上,青砖堆积高度 38cm,布置在下。
振动变送器接收单轴振动信号,钻机设备只安装了一个振动变送器,通过安装不同位置收集两种材料X、Y、Z方向的振动信号。方案一、二测量Z轴振动信号变化,方案三测Y轴振动信号变化,方案四测X轴振动信号变化。
2.2 青石与花岗岩试验方案
选用青砖和红砖作为初次试验材料,其抗压强度较低,并且堆积材料的间隙较大,对数据分析有明显影响,需要继续丰富试验内容。青砖与红砖模拟软弱岩层,将青石与花岗岩模拟为坚硬岩层。采用18cm×18cm×40cm 的青石和花岗岩材料作为试验模型。其中张后全[21]对不同尺寸青石进行单轴抗压试验后,确定青石的抗压强度范围为105.758~119.690MPa。傅伟斌[22]对不同尺寸花岗岩进行单轴抗压试验后,确定花岗岩的抗压强度范围为 71.5~93.5MPa。
花岗岩与青石作为第二次试验材料,其抗压强度较大与青砖、红砖等材料有明显不同,试验材料的完整性好、颗粒胶结程度较均匀,并且准备了多套高强度钻头、钻杆,优化了试验步骤。增加了两个量程为0~100mm/s振动传感器,可测X、Y、Z三轴振动信号;同时更换为12路采集卡,更新并升级了UMS亚为USB信号采集与记录平台;完善钻机供水系统,高压抽水泵通过软管连接至操作阀,目的是降低钻头与孔底产生的高温影响,提高降尘效果与清理岩石碎屑的能力,减少钻头对岩屑的反复研磨,提高破岩效率和推进速度。增大钻孔试验的水流压力,加快水流速度使清理岩石碎屑的能力增强,对于一些遇水易固结的岩石材料不易造成水眼堵塞,减少卡钻状况的发生。本组试验分为四组,青石组试验、花岗岩下青石上试验、花岗岩组试验、青石下花岗岩上试验,最后组合对比分析其特征规律。操作流程同青砖与红砖一致。试验如图2所示。

图2 试验方案设计
3 钻进反馈信息分析
分析钻进试验的动态参数响应规律,以岩石的抗压强度作为识别参数,根据单位体积的破碎比功值与抗压强度,确定岩石位置及结构差异。
3.1 青砖与红砖试验反馈信息分析
3.1.1 第一次青砖试验
第一次青砖试验如图3所示,初次试验时出现卡钻现象,再次试验时钻机接触试件高度为381.8mm,结束高度为891.1mm,对试件进行钻孔的长度为509.3mm,其中有效段平均速度为141.48mm/s。通过数据对比分析,Z轴振动信号在时间32:38.0激增,有明显的跃迁现象,位移值瞬间增加说明在该时间点,钻头与试件下表面相互接触,振动传感器采集数据的变化也十分明显,振动加速度扩大约3.2倍,平均转速为31r/min,转速信号基本保持稳定。
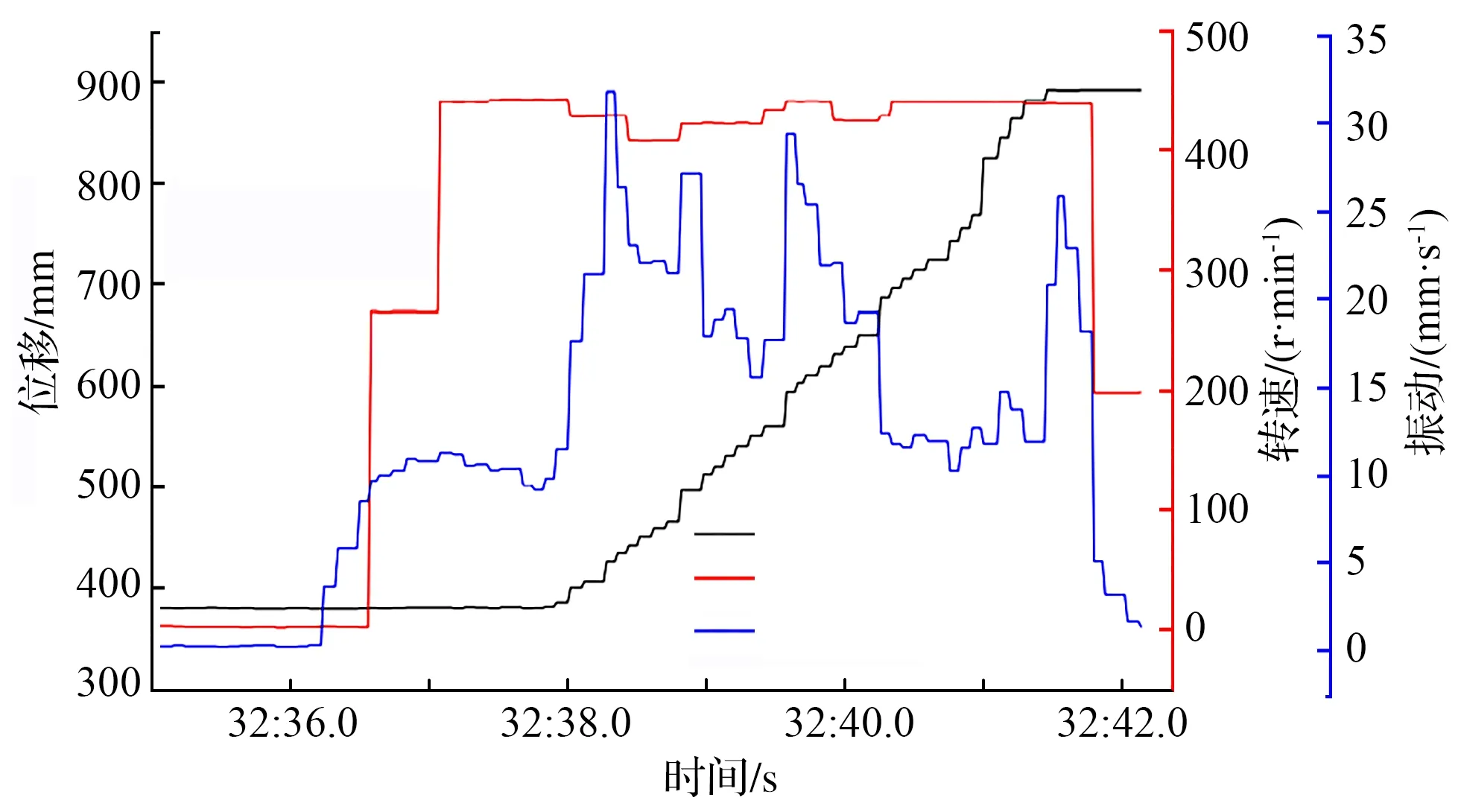
图3 第一次青砖试验
3.1.2 第一次红砖试验
在第一次红砖试验如图4所示,钻机初始高度 295.7mm,钻头与试件间预留上升高度为 20.8mm,钻头与红砖接触时位移计数值为316.5mm,结束高度698.1mm,钻进试件有效长度为381.6mm,平均速度121.78mm/s。将采集的数据提取有效钻进段参数,通过数据对比分析可知,Z轴振动信号在时间58∶56∶8出现激增,有明显的跃迁现象,位移值瞬间增加,振动加速度扩大近6倍,平均转速450r/min,转速信号基本保持稳定。
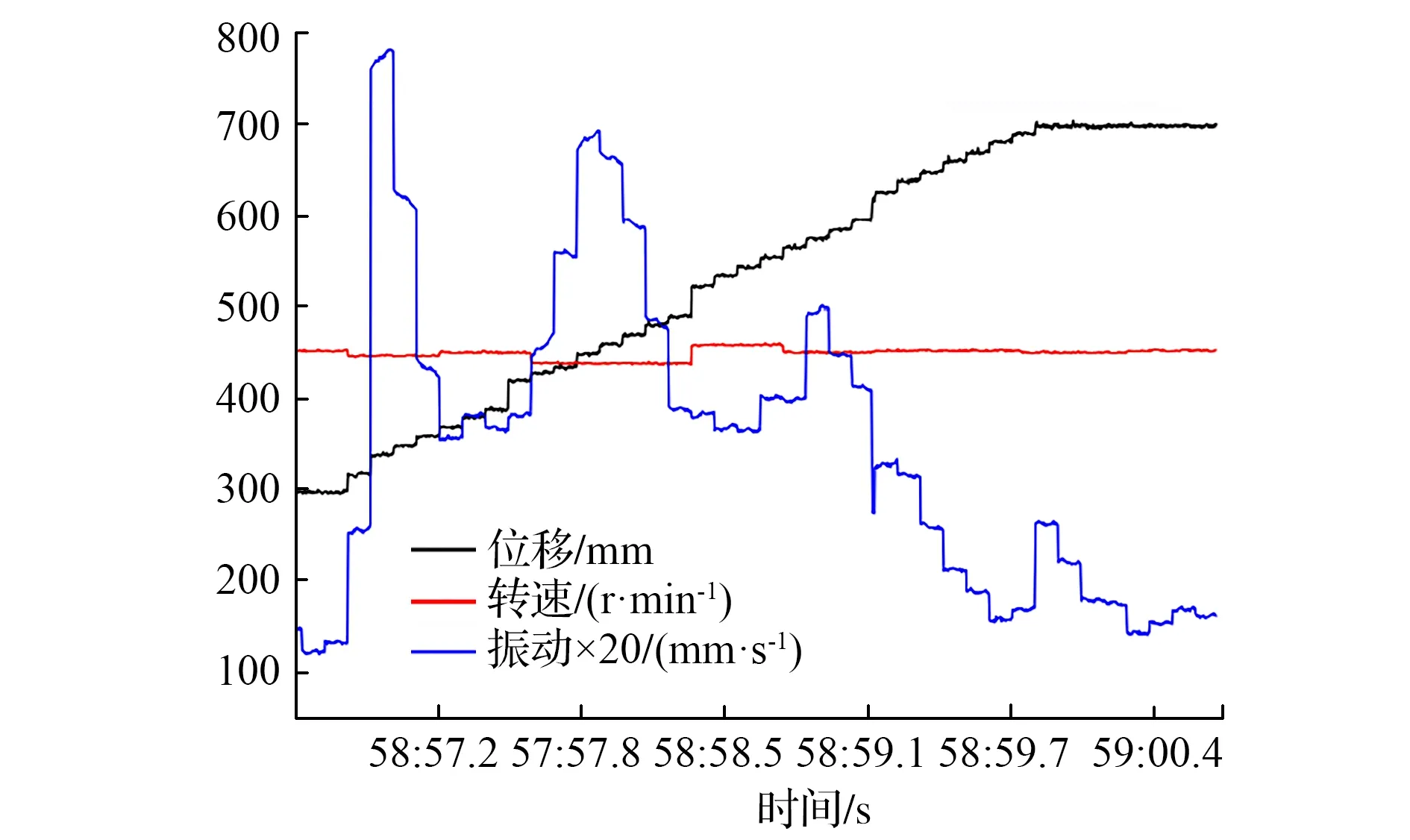
图4 第一次红砖试验
3.1.3 红砖下青砖上试验
红砖下青砖上试验如图5所示,钻机起始高度287.8mm,标注位置为实际钻头与试件接触高度为316.1mm,试验结束钻进试件高度1080.7mm,振动、推力、扭矩信号均出现跃迁现象,数值在短时间内迅速增长,其中扭矩信号上升时间要略晚于推力和振动信号,红砖和青砖堆积高度约为38cm,但砖体之间空隙较大,不能完全贴合,因此振动、推力、扭矩信号呈波浪形式,钻进至交界面处传感器信号迅速下降,通过采集的数据能够有效的确定材料所在位置及红砖与青砖数值大小的信号变化情况。
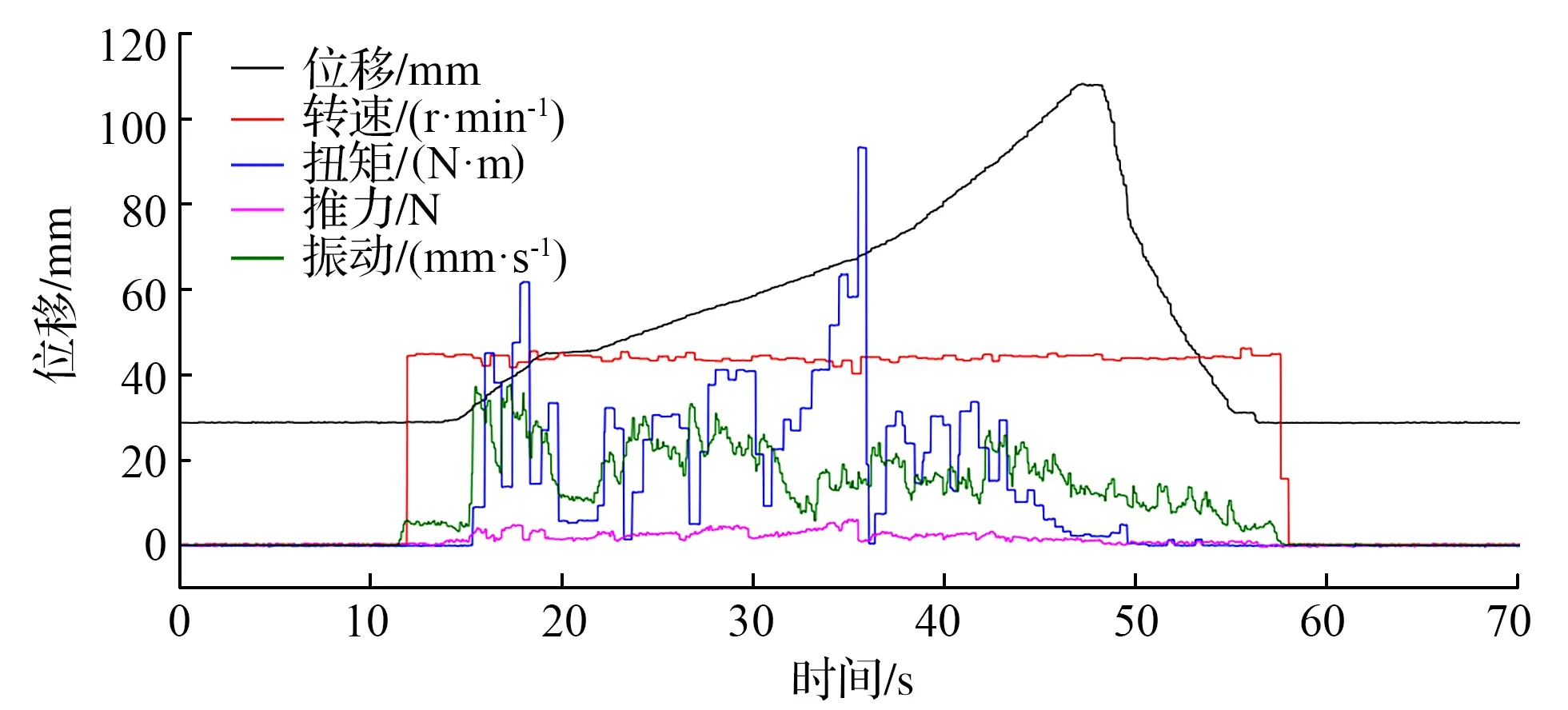
图5 红砖下青砖上试验
高度为451.3mm处,通过推力操作阀改变了初始推力大小,使得轴向推进距离增加,推进速度发生改变,红砖第一段的钻进平均速度为28.15mm/s,二段平均速度为18.13mm/s,青砖的钻进速度为36.99mm/s,是红砖平均速度的2倍。钻头由红砖钻进至青砖处,交界面处数值变化呈明显的阶梯状,从图中可以观察到青砖扭矩范围在33N·m以下,红砖的平均扭矩35.1N·m,平均推力3724.8N,青砖的平均扭矩为30.3N·m,平均推力2757.9N。
3.1.4 青砖下红砖上试验
青砖下红砖上试验如图6所示,钻机初始高度为309.8mm,钻头与试件接触高度为332.0mm,钻进结束高度为1098.5mm,振动信号、推力、扭矩在接触试件后出现明显跃迁现象,扭矩与转速信号呈明显的对称关系,由于钻进的试件不同,此时推力与扭矩数据值增长幅度发生改变,推力超过青砖阶段的最大值2.31kN,扭矩超过青砖阶段的最大值20.6N·m,钻机钻进至红砖材料时,推力和扭矩参数能较明显的反馈青砖进入红砖的过渡阶段。
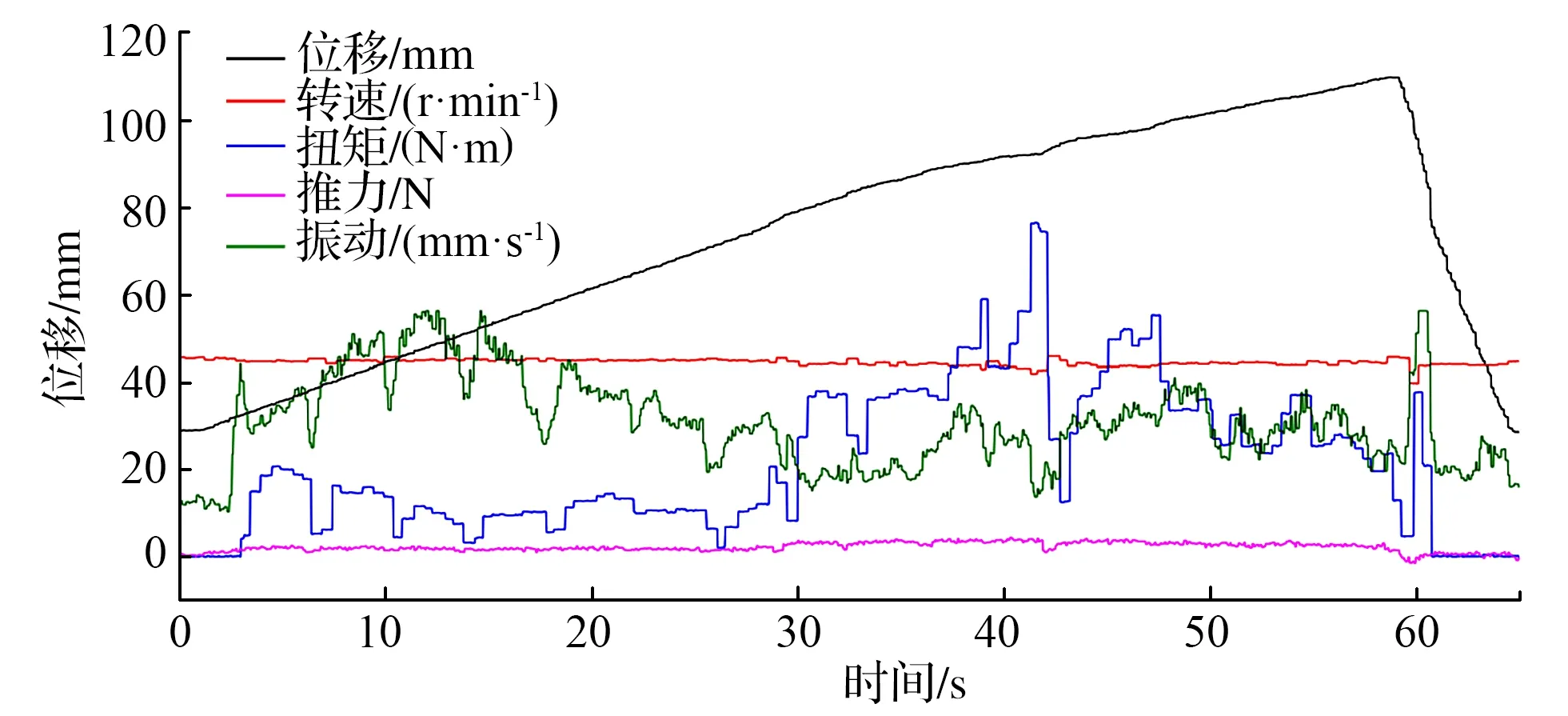
图6 青砖下红砖上试验
红砖的平均速度为15.58mm/s,青砖平均速度为17.28mm/s。青砖的平均扭矩为14.5N·m,平均推力1852.1N;红砖的平均推力3628.1N,近似青砖的2倍,通过扭矩与推力信号的强弱特点也能简单的识别出两种试验材料。
3.2 青石与花岗岩试验反馈信息分析
3.2.1 组合青石对比分析
将所有的青石试验数据提取,同种材料相互对比分析,如图7所示,推力、扭矩、推进速度、转速均是钻进过程中的变量,其中预想通过电机控制转速的大小,保持不变是完全不可能的,初始转速虽然相同,但由于转速-扭矩系统的组合旋切破岩模式,实际试验过程中一般转速随扭矩呈反比关系,当扭矩增加时转速下降,扭矩减小时转速增加。
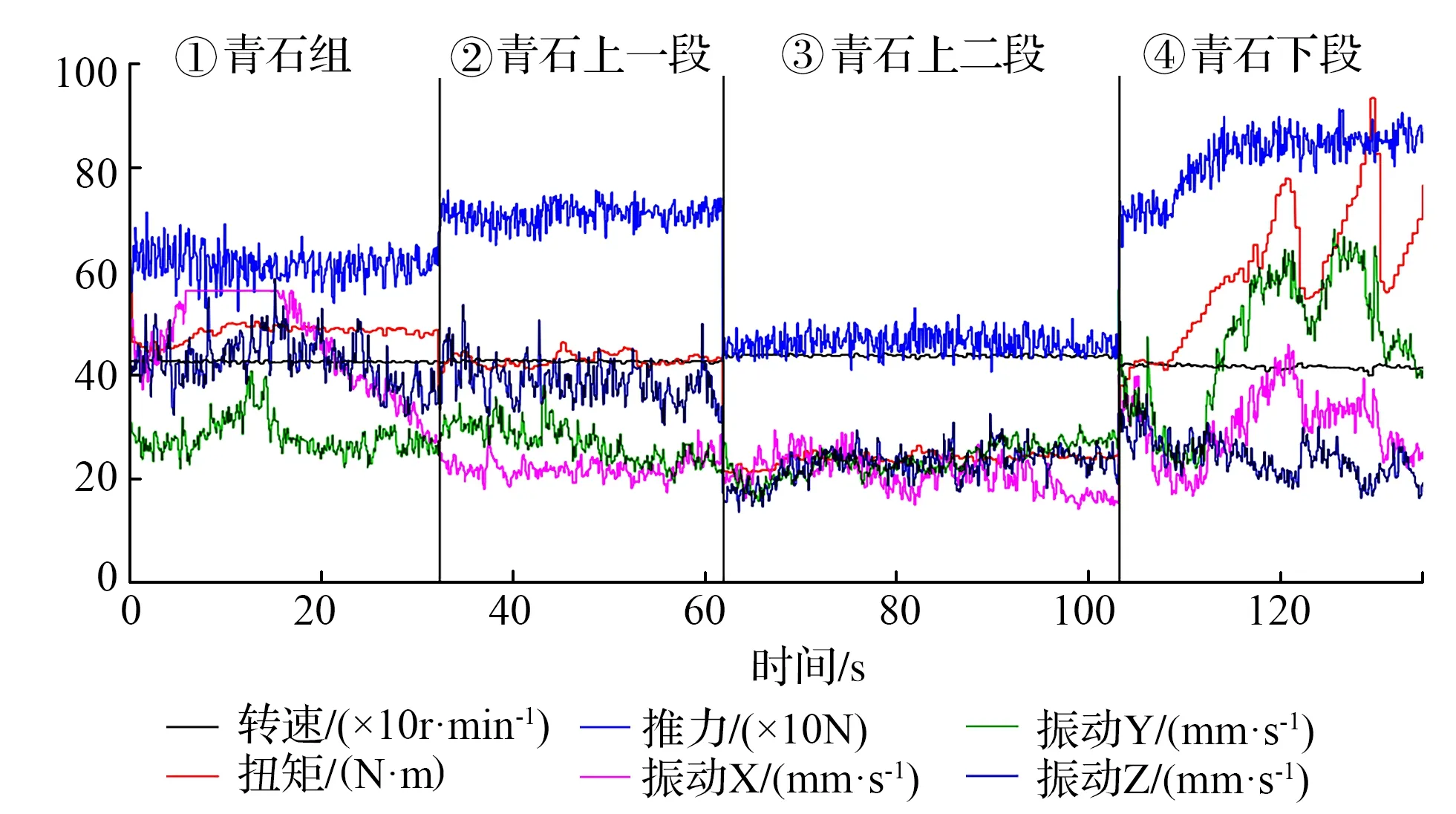
图7 组合青石对比分析
结合表1所示的钻进参数表可知,组合青石的设定为初始转速450r/min,改变推力大小的对比分析试验,①②组试验数据中,当转速相同时,扭矩值对推进速度影响效果明显,扭矩值约为推进速度的5.7倍。试验③中当扭矩缩小约1.9倍,转速下降变化值约为2倍,平均速度降低约2.4倍,说明青石试验中旋切破岩过程的扭矩是主要做功方式,与转速成反比,与推进速度呈一定的线性关系。
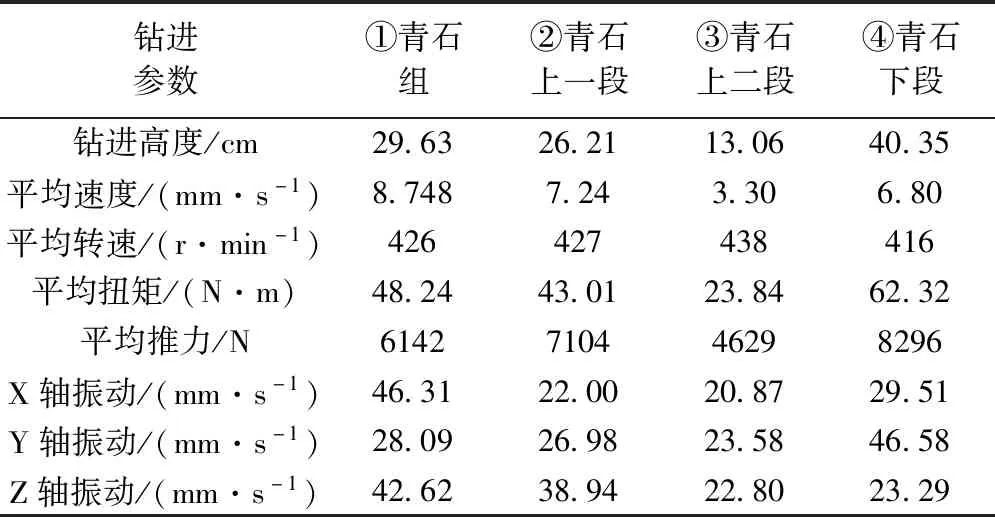
表1 青石钻进参数对比分析
3.2.2 组合花岗岩对比分析
将所有的花岗岩试验数据提取,进行各参数数据的对比分析,如图8所示,结合表1所示的钻进参数表可知,①、②组试验通过推力操作阀改变推力大小;②、③组试验对比,③组试验更换了高强度钻头。
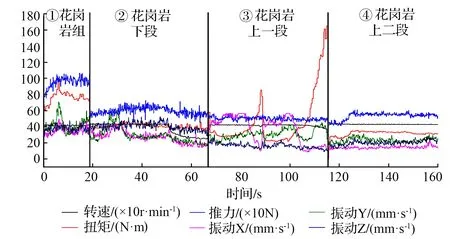
图8 组合花岗岩对比分析
①、②组实验通过改变推力的大小控制钻头轴向推进,在扭矩的作用下完成不同的剪切破坏状态,随着推力增加钻头侵入岩石的速度加快,单位时间内切削破碎岩石的体积增加,扭矩数值的增长说明了扭矩做功的增加,因此推力、推进速度、转速、扭矩等参数之间相互影响具有定量关系,在处于合理的切削岩石钻进过程中,推力与扭矩和推进速度成正比,扭矩与转速成反比。②、③实验数据表明当更换高强度钻头后,钻头的尺寸与切削能力发生改变,因此各参数间的定量关系也会发生变化,试验中要注意设备的统一。
各个传感器采集的数据见表2。
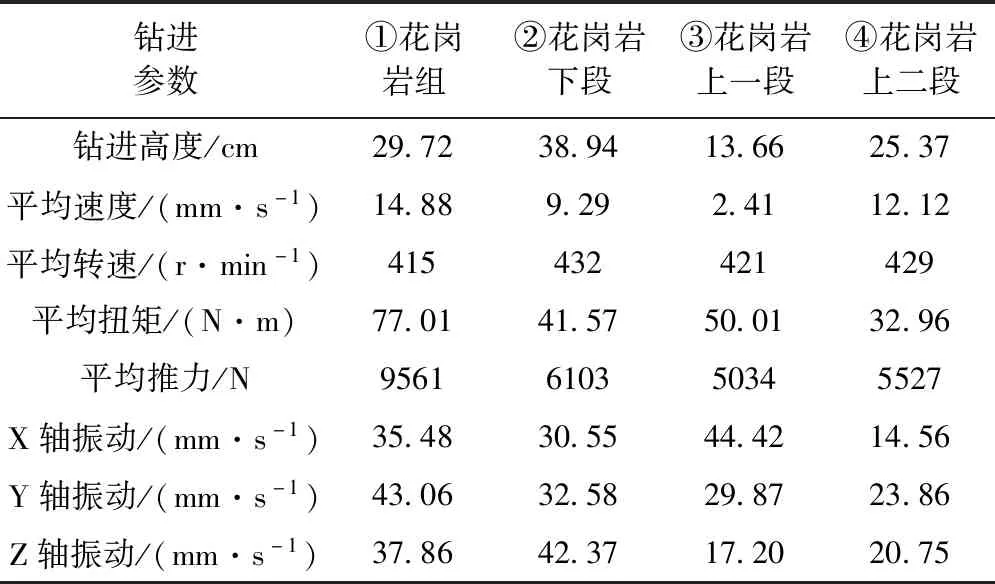
表2 花岗岩钻进参数对比分析
3.2.3 青石与花岗岩钻探试验能量对比分析
将青石与花岗岩的有效段试验数据汇总分析,如图9所示,各参数对应的岩性特征不能直观体现,因此结合单位体积的破碎比功值进行分析。
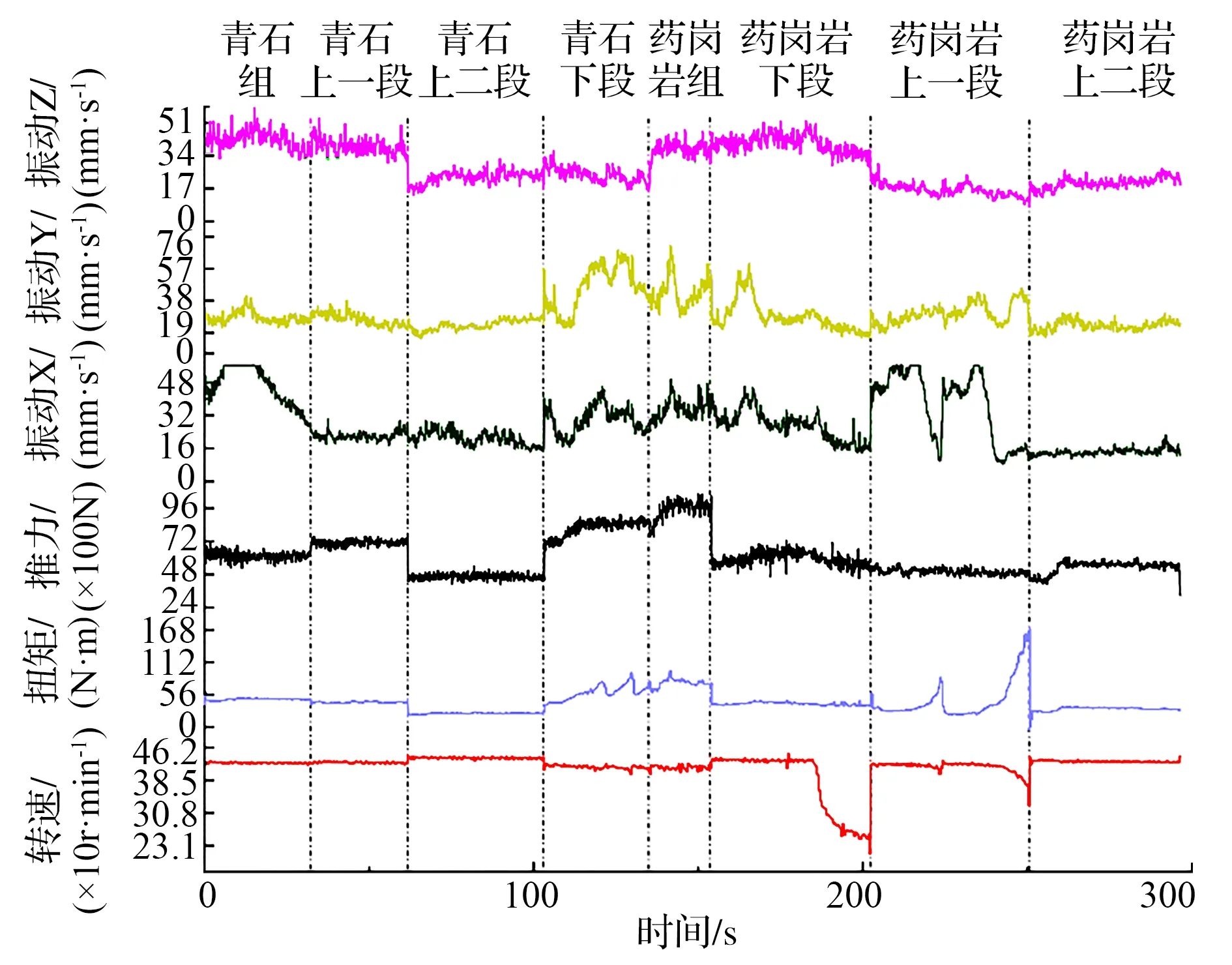
图9 青石与花岗岩钻进参数对比分析
试验条件在转速和推力通过电机分配的液压系统流量控制初始值,但与岩石接触后,转速和推力值都会受到影响,推力由于岩石产生的回弹力出现数值波动。基于能量平衡理论推导出的单位体积破碎比功值可知钻进速度、转速、扭矩、推力等参数相互影响存在定量关系。
钻机向上钻孔旋切破岩时,单位时间内钻机做功主要分为2部分,分别为扭矩-转速系统旋切破岩、剪切破碎所做的功,推力-钻速系统压入岩石,挤压破碎做功。钻机做功产生的能量主要用于切削破碎岩石和与孔底摩擦的损耗能量,如热能、振动、声响等。
试验结果根据能量守恒原理结合钻进能量理论,可推导单位体积的钻进能量比功值,即单位体积破碎比功值η,对比分析可知,青石组单位体积破碎功η值的范围为294.25~315.93,平均值为305.09,抗压强度范围为105.758~119.690MPa,取值110.724MPa;花岗岩组单位破碎功η值的范围为236.21~266.22,平均值为251.11,抗压强度范围71.5~93.5MPa,取值81.775MPa。红砖η值的范围为108.24~100.11,青砖η值的范围为47.39~47.45。
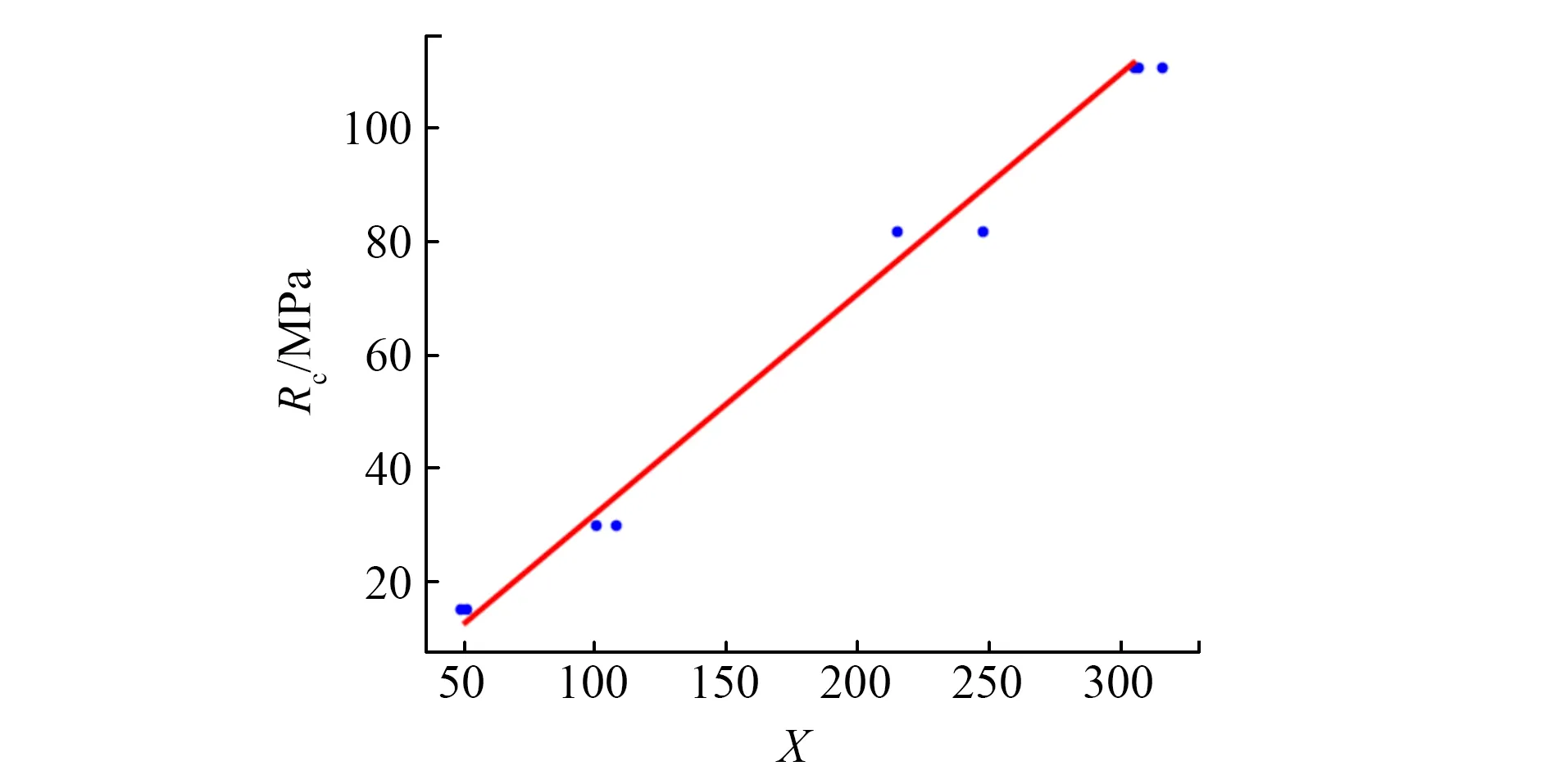
图10 抗压强度与单位体积破碎比功值的拟合曲线
如图10所示,单位体积的破碎比功值η与抗压强度运用多项式拟合的方式,X轴表示η值,Y轴表示抗压强度,拟合优度R2=0.9822,拟合后最优时的函数表达式为:RC=0.3893η-7.2639。
拟合后的单位体积的破碎比功值η与抗压强度关系公式,如图11所示,当X的最高次为1次时拟合结果最优,均方误差为28.4519,权重系数为[0,0.389255],偏置为-7.2639,随着X的最高次项逐渐增加,均方误差越大,拟合程度越差。
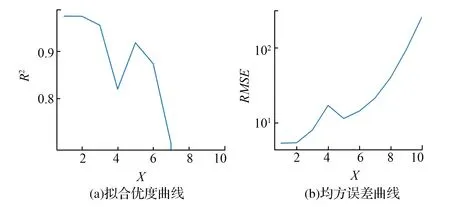
图11 拟合优度介绍
4 结 论
1)青砖与红砖试验说明,钻头与试件表面接触后各参数有明显的跃迁现象,表现为数值巨幅增长并稳定在某一数值范围。扭矩-转速旋切破岩的回转系统中,扭矩增加转速下降,扭矩减小转速增加,扭矩与转速成反比关系。当岩石强度较低、推力较大时,竖直方向钻进系统增加了推进距离,单位时间做功占比增加。
2)试验条件在转速和推力通过电机分配的液压系统流量控制初始值,但与岩石接触后,转速和推力值都会受到影响,推力由于不同岩石产生的回弹力也会导致数值波动的差异。转速信号在遇到岩石后下降量有所差异,但转速数值波动稳定。钻进速度、转速、扭矩、推力等多参量相互影响存在定量关系。
3)因钻进系统的复杂多变的特点,将多个传感器采集的试验结果融合,结果根据能量守恒原理,参照钻进能量理论,可推导出单位体积的钻进能量比功值,将单位体积的破碎比功值η与抗压强度运用多项式进行拟合,拟合优度R2=0.9822,拟合后最优时的函数表达式为:RC=0.3893η-7.2639。
