素养进阶练习设计结构要素与表现形式——以“数与运算”主题为例

浙江宁波市奉化区教师进修学校（315000）宋煜阳

任何一份练习设计，都离不开知识内容、目标指向和表现形式三个基本元素。素养进阶练习设计的关键，取决于课程内容的本质认识、课程内容所指向的核心素养理解和练习表现性任务设计。“数与运算”是《义务教育数学课程标准（2022年版）》中数与代数领域的一个主题课程内容，包括整数、小数和分数的认识及其四则运算。课程标准就“数的认识”所指向的核心素养表述有“数是对数量的抽象，感悟数的概念本质上的一致性，形成数感和符号意识”“学生经历由数量到数的形成过程，理解和掌握数的概念”；就“数的运算”所指向的核心素养表述有“经历算理和算法的探索过程，理解算理，掌握算法”“感悟数的运算以及运算之间的关系，体会数的运算本质上的一致性，形成运算能力和推理意识”。综上所述，“数与运算”主题的核心素养主要指向数感、符号意识、运算能力和推理意识，特别强调了数的概念本质上的一致性、数的运算本质上的一致性。为了凸显“一致性”这条主线，“数与运算”主题素养进阶练习设计需要在结构要素和表现形式上寻求突破。

一、“数的认识”结构要素和表现形式

数的认识，本质上是对数的结构的把握，而数的结构需要用结构要素去表达。无论是整数、小数，还是分数，在数的结构上均保持了一致性，都是对多少个计数单位的表达。比如，314由3个百、1个十和4个一组成，表示为314=3×100+1×10+4×1；3.14由3个一、1个十分之一和4个百分之一组成，表示为3.14=3×1+1×0.1+4×0.01由2个三分之一组成，表示为一个数的结构，需要用十进制计数单位、位值、数位（数级）等结构要素去表达，是“数的认识”练习设计的核心要素。

“数的认识”核心要素的表现形式，一般反映为数量的抽象程度和数的表征方式两个方面。数量的抽象程度，主要表现为“具体—半具体半抽象—抽象”。数的表征方式，主要表现为动作表征、图像表征、语言表征、符号表征、情境表征等。

那么，不同抽象程度的学习材料该如何选择呢？显然，需要根据学生的年龄特征、数的结构复杂程度来综合考虑。比如，“捆”是计数单位“十”的物化材料，经常以实物或实物图呈现，一般供教学“10以 内 数 的 认 识”“11~20各 数 的 认 识”“100以 内数的认识”时使用；一个小方块（一）、一条块（十）、一个面方块（百）、大立方体（千）等实物或实物图，一般在教学“100各数的认识”“1000以内数的认识”时使用，都属于具体的学习材料。计数器和数轴都属于半具体半抽象的学习材料，贯穿于整数、小数的教学；数位顺序表属于抽象的学习材料，常在教学整数和小数时使用。

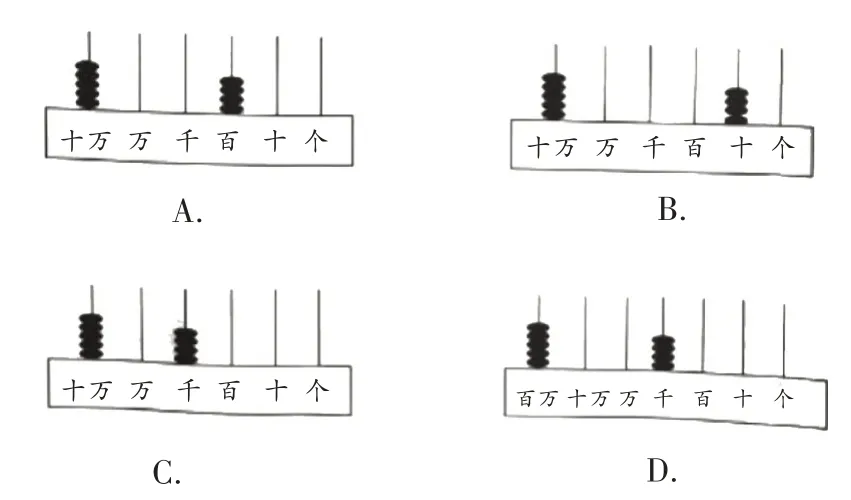
练习1下面表示500 400的数是（）。

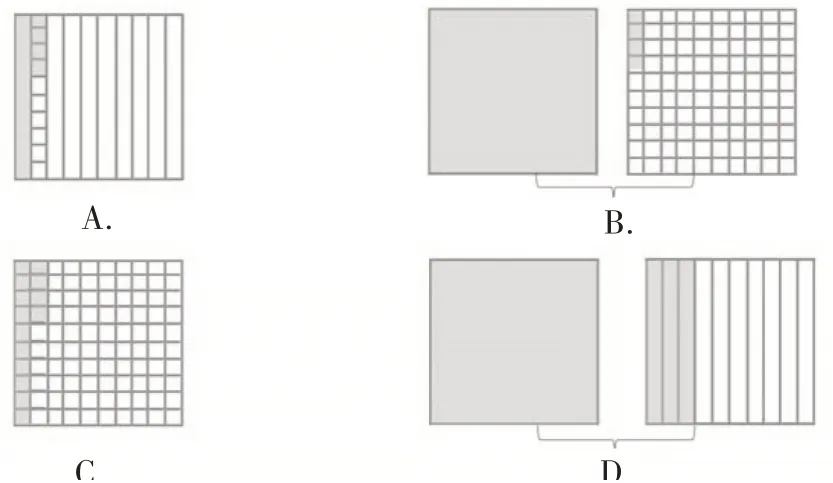
练习2用一个正方形代表1元钱，那么阴影部分表示“1.30元”的图是（）。

练习3数轴上点A用小数表示是（），用分数表示是（），再添上（）个这样的分数单位就能变成最小的质数。数轴上点B表示的数是（）。

练习1至练习3，分别采用计数器图、方格图、数轴来表达数的结构，都属于典型性学习材料，分别随着年级升高而逐步抽象。

练习4在数线上用★表示60 300的位置，正确的是（）。

练习5请根据第1、2幅图的写数规律，写出第三幅图所表示的数。

写作：1 0050 0030

写作：2 0010 0305

写作：（ ）

练习6左图是用台秤称菠萝时台秤显示的菠萝的质量，右图是另一个台秤。请你在右图台秤上用箭头标出菠萝的质量。

练习4至练习6分别围绕计数单位、数位顺序表、进制进行设计。其中练习4采用相同的数线引导学生对计数单位“十”“百”“千”进行辨认；练习5采用水果替代数位顺序表引导学生读数、写数；练习6则在“十进制”与其他进制的对比中引导学生体会计数单位的变化。这些变式练习都能帮助学生理解计数单位的本质，进一步认识数学核心要素。

数的表征方式，重点强调各种表征方式的综合运用以及方式之间的切换，从操作、图像、叙述、解释、举例等维度对数的概念进行具体化和形式化两个层面的表征。

比如，在认识“1000”这个数时，浙教版教材以“大家来说1000”的举例形式实现各种表征方式的综合运用。

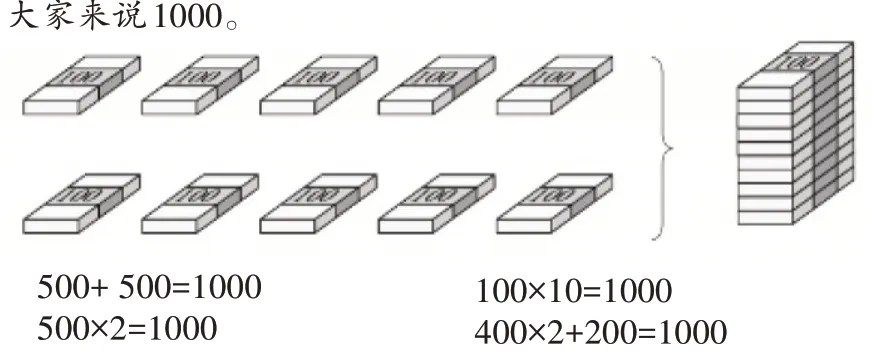
围绕“10个百”的意义，采用了多层次的表征和多元化的结构表达：有操作层面的“10个百”实物图像的情境表征，有加法、乘法、乘加多种方式的符号层面的符号表征和语言表征。

又如，在“1～5的认识”练习中，可以采用画一画、圈一圈、写一写的方式进行表征。

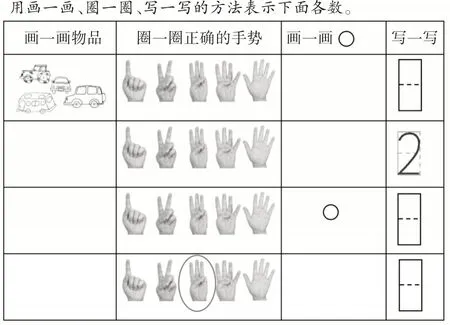
对数进行表征，其中就有动作表征、情境表征、图像表征、符号表征等，这是通过给出某种表征的信息来填充其他表征。这样的练习不仅表征手段丰富，而且重视表征方式之间的切换，能从多个维度帮助学生体会从数量到数的抽象过程。

数概念的一致性体现为计数单位是建构数的基础，认识计数单位是数的认数关键。在设计“数的认识”练习时，要始终把计数单位作为核心，围绕数位顺序表、位值等核心要素对数进行多层次表征和多元化表达，促使学生充分体会数量抽象为数的过程。同时，利用基于数轴等学习材料的填数练习，能够帮助学生体会整数、小数、分数之间的内在联系，体会数与数轴上点的对应性、小数的稠密性和分数的等价性。

二、“数的运算”结构要素和表现形式

算理和算法是数的运算的“双核”，也是练习设计的主要对象。计数单位、运算律和等式的性质是算理和算法的基础。为此，在设计“数的运算”练习时，要围绕计数单位、运算律和等式性质。

整数、小数和分数的加减法运算，在算理上都反映为“相同计数单位个数的加减”，在算法上表现为“相同计数单位上的数字相加减，计数单位不变”。为此，在数的加减运算练习设计中，需要围绕算法上的“相同数位对齐”、算理上的“相同计数单位个数相加减”这条主线，设计看图填空、画图表征、解释说理等题型。

练习1在算31+25=（ ）时，聪聪是这样算的，你知道“3+2=5”表示什么意思吗？请在方框里画一画。

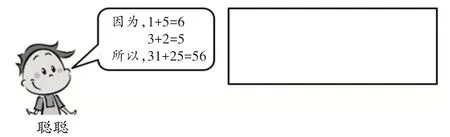
练习2一本练习本和一套三角尺共多少元？下面分别是聪聪和明明的计算方法，你同意哪个？写出你的理由。

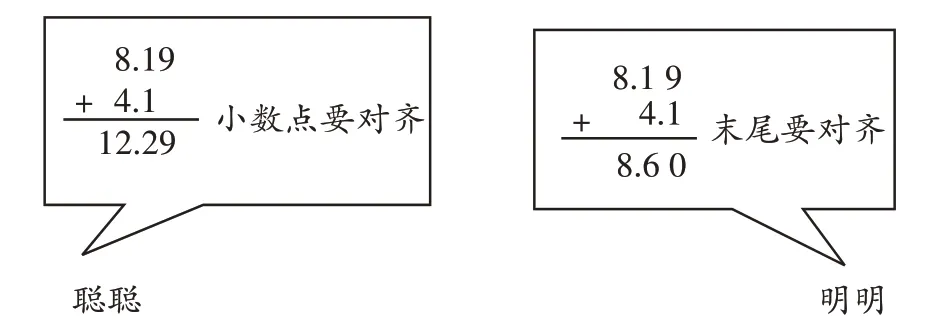
练习1是两位数加两位数的口算，对“相同数位上的数相加”背后的原理进行了表征；练习2是小数加法笔算，围绕“小数点对齐”和“末尾对齐”进行辨析和说理，都指向了理解算理。

乘法和除法运算的一致性体现为计数单位与计数单位相乘或相除、计数单位上的数字与计数单位上的数字相乘或相除。整数乘除法、小数乘除法在算理层面贯穿了计数单位的个数累加或均分的过程，保持了运算之间算理的一致性。比如，整数除法140÷4，运算步骤为“14（十）÷4=3（十）……2（十），2（十）转化为20（一），20（一）÷4=5（一），最后把3（十）、5（一）组合成35”，关键在于把被除数拆分为以不同计数单位为单位的若干部分进行均分。练习设计需要加强这个运算程序的梳理，可以结合小棒操作流程图，让学生填写除法竖式，如“84÷3”就可以采用下图来考查学生对算理和算法的过程性理解。

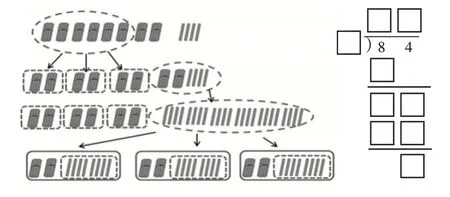
上述列举和讨论的内容都是围绕计数单位，下面将讨论有关运算律的习题设计。与算理、算法关联最紧密的当属乘法分配律，所以乘法分配律的本质属性和运算应用是“数的运算”练习设计的重要考查对象。

因为乘法分配律一般是通过不完全归纳推理得出，所以对规律的理解可以通过解释说理、举例说明的方式进行。下面的题组就充分反映了这一思路。

（1）聪聪计算78×73+78×27时，采用了“78×73+78×27=78×（73+27）”的计算方法。聪聪这样算所依据的运算定律是什么？

（2）将计算下图面积的过程填写完整。

这个图形的面积是16×15+14×15，运用（1）中的规律可以得出：

16×15+14×15=（○）×15=（）（平方厘米）

（3）请举一个可以用（1）中的规律解决问题的生活例子。

该题组在学生回忆运算定律的依据、面积模型的基础上，鼓励学生自己举例说明，在乘法分配律的举例验证活动中对运算定律不完全归纳推理的应用进行了考查。

应用乘法分配律在课程标准的核心素养“运算能力”的主要体现是：提出了“能够清楚运算的对象和意义”“选择合理简洁的运算策略解决问题”等要求。像“计算49+98×48+47”这道题能考查学生能否整体观察数据，能否保持敏锐的数感，能否识别到“49+98×48+47=98×48+96=98×48+48×2=48×（98+2）”这个过程。又如，江苏南京四年级期末调研测试卷就围绕乘法分配律的应用设计了如下题组：

数学课上，李老师让大家比较“9×9+19”与“10×10”的大小，大部分同学根据计算的结果判断出它们相等。爱较真的轩轩激动地说：“我能通过推理说明两个式子相等。”她边说边写（见下图的左框）。

听了轩轩的想法，大家眼前一亮，不禁跃跃欲试。李老师接着出示“99×99+199”，让大家填写：

（1）99×99+199=（ ）×（ ）；

（2）请在右边方框中写出推算的过程。

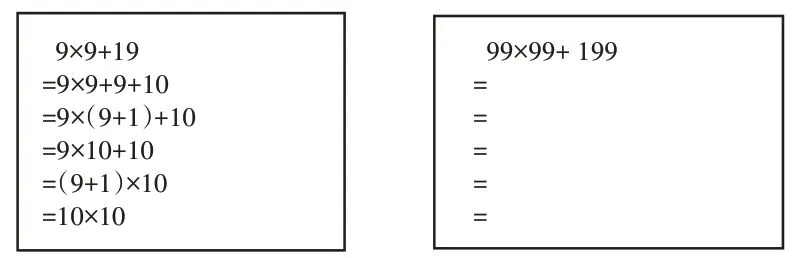
该题是以题组的形式，通过创设数学情境激活学生的探究欲望。学生在自主探究、互动交流中积累了多次运用乘法分配律解题的经验。

上述对“数的认识”“数的运算”结构要素和表现形式进行了讨论，其实“数的认识”“数的运算”本身是同一个主题，联系非常紧密。比如，整数笔算乘法是基于乘法意义的“求和模型”、位值制、计数单位个数、乘法分配律的综合运用，是算理的一次升级，是融数的认识、数的运算为一体的综合活动。在素养进阶练习设计中，教师只有抓核心、悟结构、寻联系、促迁移，才能有效落实核心素养目标。