基于室内地图推演与信号穿墙修正的定位优化方法

孙大洋，石文孝，张定国

（1.吉林大学通信工程学院，吉林 长春 130012；2.巴斯大学自主机器人研究中心，巴斯 BA27AY）

0 引言

室内高精度定位作为一项基础技术在各行各业中发挥着重要作用[1]，如何提高复杂环境下室内定位系统的定位能力是一个重要的研究课题。在众多室内定位技术中，超宽带技术（UWB,ultra wide band）[2]与红外线、蓝牙、超声波、射频识别等技术相比，不仅具有数据传输速率高、抗干扰和穿透能力强等优点，还可以达到更高的定位精度[3]。UWB 技术若采用双边双向测距（DSTWR,double-sided two-way ranging）算法[4]，其测距误差主要来源于测距节点晶体振荡器的频率误差与节点间的时延差，在节点间无显著障碍物阻挡的情况下，测距精度可达厘米级[5]。

然而，“节点间无显著障碍物遮挡”这一场景过于理想，室内空间构成复杂多变，非视距（NLoS,non-line-of-sight）传播的影响普遍存在，并且会产生多径效应，影响定位精度[6]。因此在室内定位中，减小NLoS 传播影响对提高定位精度十分关键。已有学者在很多方面对NLoS 的影响进行了研究[7-8]，如NLoS 识别[9]、NLoS 路径定位[10]及NLoS 消除[11]等。由于NLoS 会带来较大的测量误差，使用NLoS 测量结果进行定位求解必然会影响定位精度，因此可采用简单移除NLoS 测距的方式进行定位算法改进，提高定位精度。NLoS 识别即可用于这种改进，使用NLoS 识别结果移除NLoS 测距，之后使用视距测量集合进行定位。但该方法仅从分类层面对测距误差进行限制，不能最大效率地提高测量信息的利用率，在测距信息较少的情况下也会因为视距测量较少而无法定位。利用NLoS 路径进行定位是基于散射体信息的方法，适合传播路径有可规避障碍物的场景，不适用于信号穿墙传播情形。NLoS 消除的解决思路更多的是将NLoS 的特性与形成机理考虑进来，不单纯以NLoS 识别为目标，因此可以更有效地对测量信息加以利用。在室内NLoS问题的众多成因中，墙体是空间结构中的主要因素，在室内环境中具有普遍性，对于以墙体遮挡为主的NLoS 误差，如能建立可应用于实际测量的信号穿墙模型，即可最大限度地消除非视距误差对定位结果的影响。

由于不同墙体内部材料及结构具有复杂性，对无线信号穿墙折射的真实模型进行建模较为复杂。有学者研究了UWB 信号穿墙单次折射模型下消除NLoS 误差的性能[12]，表明了单次折射模型减小穿墙定位模型中NLoS 误差影响的可行性。在后续的研究中，文献[13]在假设已知室内场地的实际大小的基础上，搭建信号穿墙传播模型，分析模型下定位误差，得到该模型能够有效减小NLoS 误差的结论；文献[14]采用了等效源法[15]进行近似，利用UWB 节点与墙体间几何关系，搭建信号穿墙传播模型，在已知入射角的情况下对穿墙定位进行仿真，由NLoS误差信息对到达时间（ToA,time of arrival）方法的测距结果进行修正，以提高测量精度。

从穿墙传播模型的建立到在定位模型中的使用，不仅某次信号传播是否隔墙需要已知，判定是否使用该模型还涉及穿墙传播模型的无线信号穿墙入射角、墙体介电常数、厚度等参数，这些都会对定位结果的精度产生影响。而且由于墙体施工的不一致性，墙体规格、材料都存在很大差别，甚至无法获得，如空心砖墙体涉及的参数就更多，情况就更为复杂。自无线信号穿墙传播的等效源法[15]提出以来，目前科研人员对于穿墙定位的讨论还是以信号传播模型的研究或定位系统的仿真为主，仍需要已知信号穿墙入射角或墙体厚度、介电常数等信息才能定位。

本文在上述研究的基础上，通过对信号入射角度的合理近似，以及墙体参数的一致化处理，弱化了穿墙传播模型在实际定位模型求解中的约束条件，以飞行时间（ToF,time of flight）测距为基础，提出了一种基于室内地图推演与信号穿墙修正的定位优化方法。该方法采用信号穿墙单次折射模型，结合地图推演的方式对目标进行定位，不需要已知墙体厚度、相对介电常数以及信号穿墙入射角，即可计算出定位坐标，同时具有较高的精确度。

1 无线信号穿墙传播测距模型

视距条件下，经典的ToF 测距[16]需要根据无线信号在节点之间的传播时间Δt和光速c计算出节点之间距离s，即

在墙体阻隔的典型非视距情况下，由于无线信号在墙体内的传播速度和传播方向都会发生改变，若不考虑信号穿墙特性，穿墙测量距离往往大于信号传播的实际距离，就会导致定位偏差。为简化验证，本文仅考虑节点位于同一水平面上的二维穿墙场景，如图1 所示的信号穿墙传播模型中，2 个节点分布在墙体两侧，假设墙的厚度为dwall，墙的相对介电常数为ε，而墙的相对磁导率μ近似为1，信号穿墙入射角为α，在墙体内传播折射角为θ，参考节点的坐标为(a,b)，定位节点的坐标为(x,y)，则2 个节点间的直线距离为

图1 信号穿墙传播模型

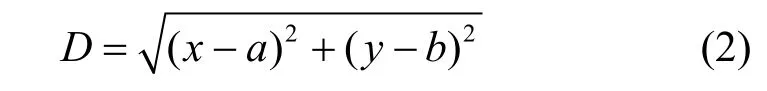
假设光速为c，墙内传播的信号波速可以近似认为满足

根据无线通信原理，仅考虑信号在墙内传播时发生单次折射的情况，信号在墙内的等效传播距离d＇为[17]

结合式(3)和式(4)可得，墙体内传播的额外时延为

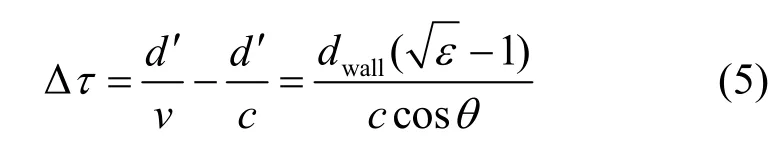
依照图1 的信号穿墙传播模型，由斯涅尔折射定律[18]，有

在实际环境中，α通常是未知的。本文为简化模型计算难度，在模型的构建中采用了近似处理：将α认为是2 个节点间直线与墙体所成角度。在节点间距离远大于墙体厚度的情况下，即D＞＞dwall时，可以认为α和两节点直线与墙所成角度之间的差值对计算的影响可以忽略[19]。经测算，在假设α为45°时，近似角度仅与实际角度偏差0.5°，故该假设在一般锚点间摆放距离足够大的测距场景中是适用的。采用近似方式拟合α，有

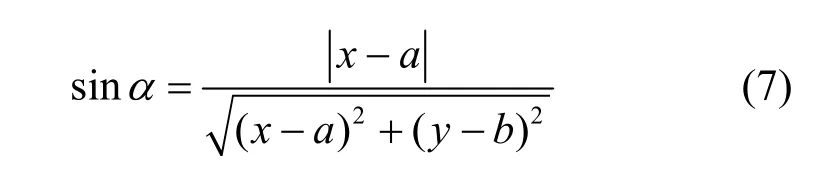
折射模型中，信号传播的等效距离可以利用余弦定理进行求解，由式(2)、式(6)及式(7)整理可得

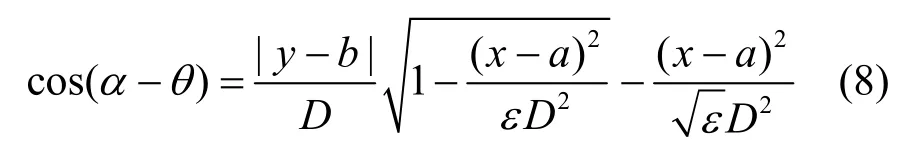
根据图1 模型，结合式(2)和式(8)，利用几何关系可计算出信号传播的几何距离dG-path为

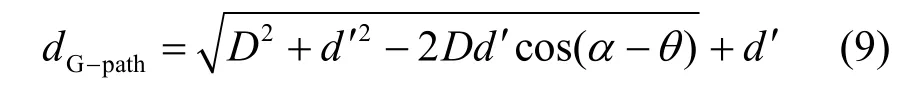
设由节点获得的信号传播时间为δt，满足

将式(4)、式(5)、式(8)和式(10)整理可得

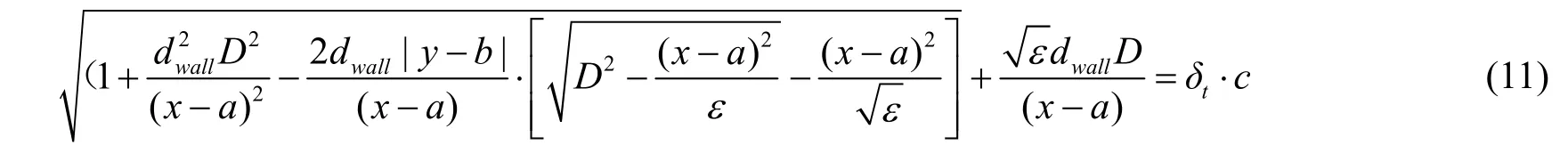
由此，获得了无线信号穿墙传播模型中信号传播时间与节点位置、墙体厚度以及墙体介电常数之间的函数关系。当α=0时，式(11)为

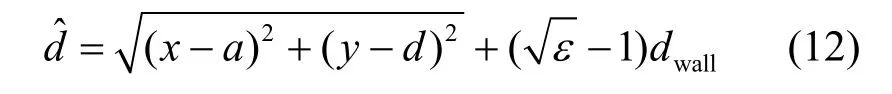
与信号传输路径垂直墙的情况计算所得表达式一致[15]，可视为信号在墙内不发生折射。

2 考虑信号穿墙传播的定位模型

在本文推导的无线信号穿墙传播测距模型的基础上，对室内定位中基于测量的多边定位模型进行了改进，获得本文提出的考虑信号穿墙优化的定位（TWO-L,through-wall optimized localization）模型。锚点与定位节点间的位置关系有2 种：一种是隔墙，另一种是不隔墙。在满足图1 推导模型计算条件D＞＞dwall的情况下，锚点可以随意摆放在墙内或者墙外，与定位节点通信获取定位节点与锚点群间的信号传播时间，如图2 所示。

图2 锚点群与定位节点的分布示意

结合无线信号穿墙传播测距模型，定义一个穿墙标志变量N=｛N1,N2,···,Ni,···,Nn｝，Ni=1表示锚点i与定位节点间使用信号穿墙模型，Ni=0表示锚点i与定位节点之间使用视距传播模型。假设利用UWB 获得的距离信息d=｛d1,d2,d3,···,dn｝，模型求解方程组为

因此在二维空间中，穿墙定位问题转化为在测距信息与锚点坐标已知的情况下按照式(13)求解定位节点坐标的问题，只需锚点个数大于或等于4 即可满足方程组有唯一收敛解的求解条件。据此本文定义目标函数为

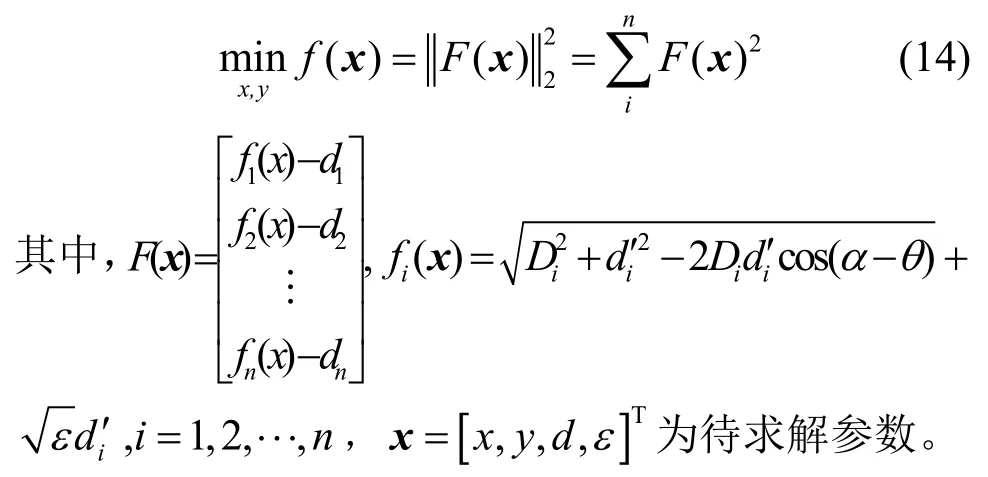
利用Levenberg-Marquardt 方法[20]求解该目标函数，搜索方向可设置为

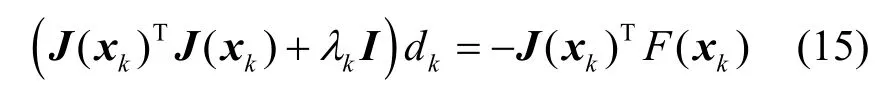
其中，J(x)为F(x)的Jacobian 矩阵，标量λk控制搜索方向dk的幅值和方向，dk为优化函数的下降方向，I为J(xk)TJ(xk)中的对角项矩阵。

由于Levenberg-Marquardt 方法的求解需要设置初值x(0)，故可先利用多边测量方法，忽略墙体厚度影响，获取定位节点近似坐标作为求解初值。当各堵墙的厚度及建造材质近似相同时，可将各堵墙视作一致进行定位求解，这种近似并不会对模型求解定位节点坐标造成太大的偏差。本文对此进行了仿真验证，实验场景如图3 所示。

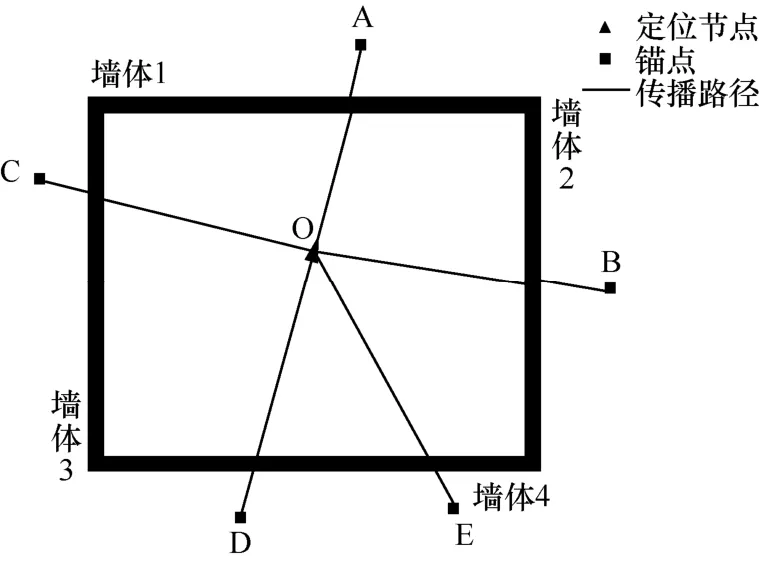
图3 实验场景

假设实验场景中4 堵墙的墙体厚度与相对介电常数设置如表1 所示。

表1 4 堵墙的墙体厚度与相对介电常数设置

本文进行了两组仿真实验，一组墙体参数设置如表1 所示，另一组所有墙体参数均设置为与墙体1 一致。将两组实验的坐标结果采用欧氏距离计算坐标偏差值[21]，仿真中测距方差设置为10，进行了100 次实验，累积分布函数（CDF,cumulative distribution function）曲线如图4 所示。

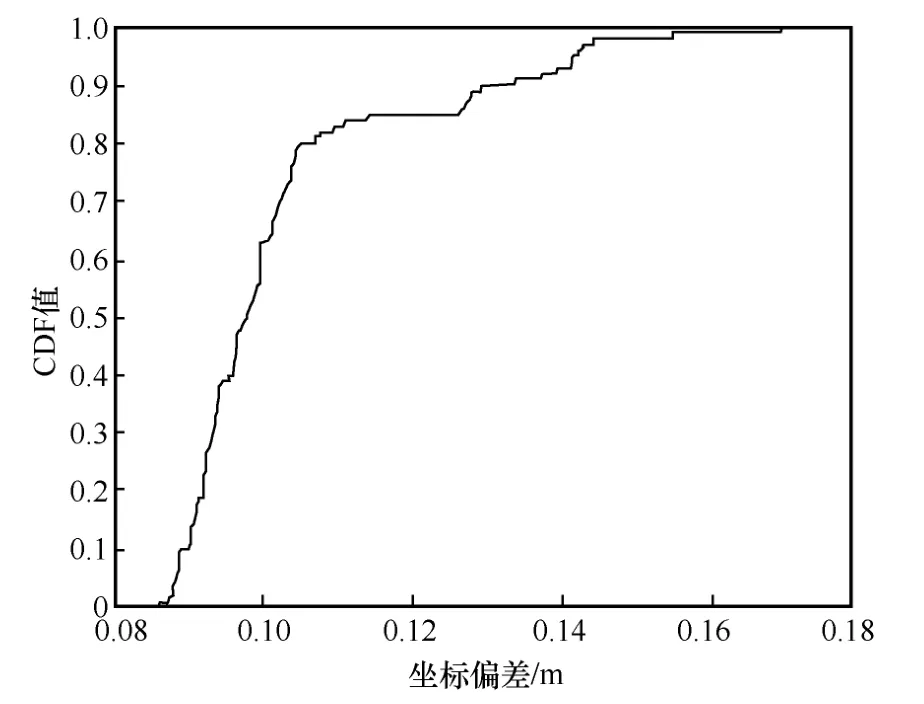
图4 两组仿真实验坐标偏差CDF 曲线

由图4 可知，坐标偏差大概率集中在0.16 m 以内，因此，在墙体厚度与材质相差不大的情况下，对墙体做近似相同处理是可行的。在实际应用中，在同一室内环境下墙的厚度及建造材质的相对介电常数也是近似一致的，因此本文推导的定位模型具有较强的适应能力，可以匹配多种测距定位场景。

3 结合地图推演的穿墙定位模型

第2 节中探讨的模型确定了已知穿墙标志向量条件下定位坐标的求解，但在实际应用中，定位节点与锚点间隔墙的关系可能由于定位节点的移动而改变，因此如何自动获取穿墙标志向量也是值得探讨的问题。利用深度学习的方法对UWB 非视距误差进行识别是一种方式[22]，结合地图推演是另一种方式，本文采用地图推演方式。在图3 建立的模型的基础上，本文考虑利用多边测量方法，搭建一个能够估计定位节点所处位置进而获得穿墙标志向量对定位节点坐标进行求解的模型。

在已知锚点坐标与室内地图的条件下，首先利用定位节点与锚点间的距离信息由多边测量方法计算出定位节点的推演位置；然后根据推演位置与室内地图进行定位节点与锚点之间是否隔墙的判别，如果推演位置与锚点之间的线段与墙体线段相交，设置穿墙标志为1，否则为0；最后根据穿墙标志向量建立穿墙定位模型，使用推演位置迭代计算定位节点的修正位置。地图推演判定穿墙标志向量的流程如图5所示。

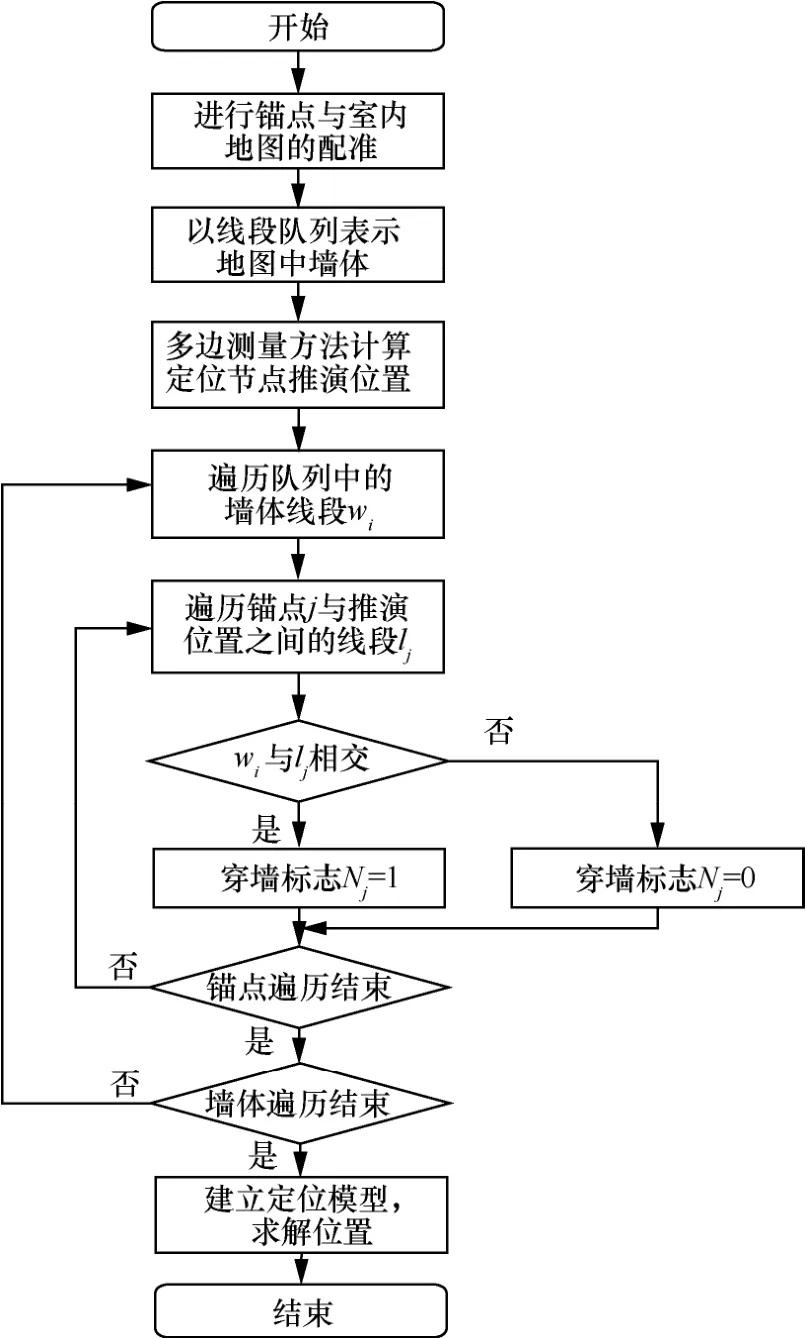
图5 地图推演判定穿墙标志向量的流程

由于在假设无墙的情况下计算推演位置将会引入计算偏差，对于该偏差是否会对穿墙标志向量产生误判的问题，本文进行了实验分析，使用UWB测试了以厚度为30 cm、相对介电常数为4.43 的墙为实验条件的测距偏差，节点分布如图6 所示。

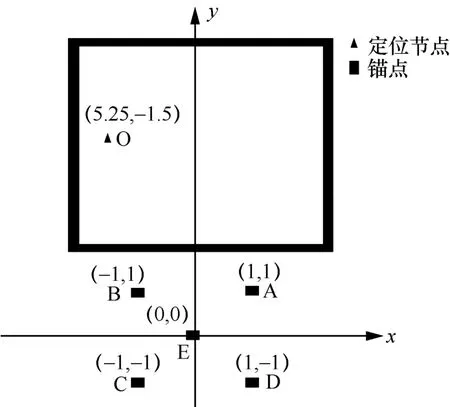
图6 实验场景中节点分布

图6 绘制了各节点的坐标值，对定位节点O 进行测距，将距离值与利用式(2)计算的距离相减，所得测距偏差结果绘制成CDF 曲线，如图7 所示。

图7 信号穿墙传播测距偏差CDF 曲线

由图7 可知，测距偏差随节点位置的不同而呈现出不同的偏差区间。若穿墙标志向量的计算结果出现偏差，则位置偏差应大于0.30 m。因此，在使用地图推演模型时只要定位节点不紧靠墙壁，推演位置就可以相对准确地对隔墙情况进行判别。对于定位节点紧靠墙壁情形，由于信号穿墙、反射等特性较为复杂，本文不进行深入讨论。

考虑到锚点与定位节点的位置关系将对定位误差产生影响，本文在二维平面上对锚点与定位节点的几何分布进行分析，用几何精度因子（GDoP,geometric dilution of precision）作为度量指标。根据图6，在20 m×20 m 的空间内选取定位节点，绘制定位节点内GDoP 分布，如图8 所示。由图8 可知，对于场景内不同的定位位置，锚点分布会对定位结果产生一定的影响。

图8 定位节点内GDoP 分布

4 实验验证与性能分析

为验证地图推演穿墙定位模型的有效性，本节分别通过仿真实验和UWB 实测实验的方式对模型进行了验证。

4.1 仿真实验

依照考虑信号穿墙的定位模型，选择了5 个UWB 节点作为锚点，假设墙体厚度d=30 cm，相对介电常数ε=4.4 3，测距信息模拟UWB 测量，测距误差服从N(0,σ2)正态分布，其中，方差设置为σ2=10。按照无线信号穿越的是否为同一堵墙，本文设定了锚点坐标与墙体结构的2 种仿真场景分别如图9 和图10 所示。

图9 仿真场景1

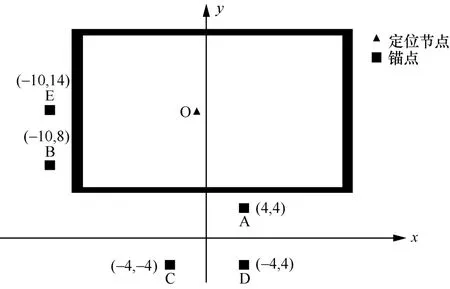
图10 仿真场景2

对于仿真场景1，取定位节点坐标为(-1.83,5.72)以及(2,8)；对于仿真场景2，取定位节点坐标为(-1,11)以及(6,10)。仿真中进行了多组实验，将本文提出的TWO-L 方法与经典的最小二乘（LS,least square）法[23]以及使用加权最小二乘法的平方测距定位（SR-WLS,squared-range and weighted least square）方法[24]的定位误差进行了对比，SR-WLS方法将穿墙测距统一看作NLoS 测距，并对信号穿墙导致的NLoS 测距值进行了修正。2 种场景下不同定位节点处的仿真结果分别如图11～图14 所示。

图11 仿真场景1(-1.83,5.72)处仿真结果

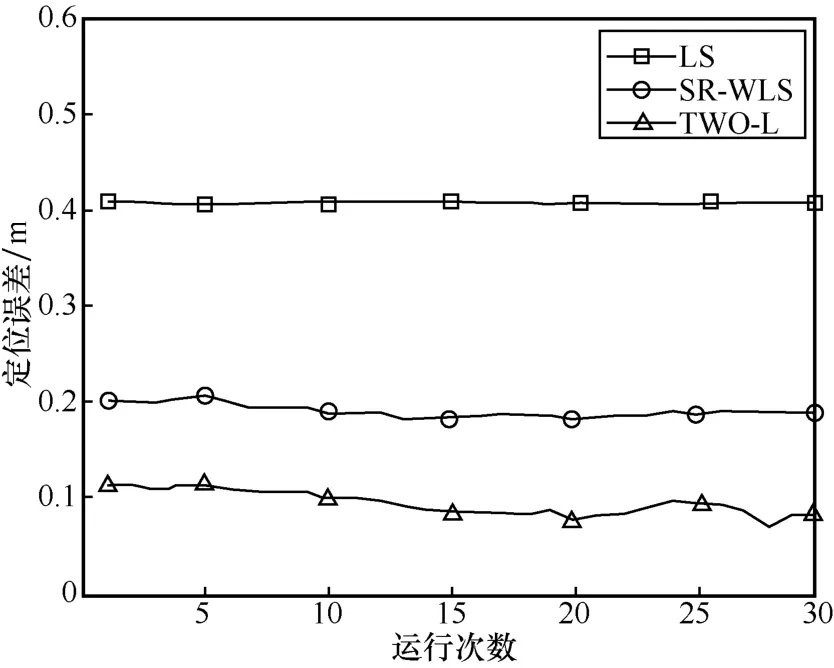
图12 仿真场景1(2,8)处仿真结果

由图11～图14 可知，定位节点在室内典型位置的情况下，本文所搭建的模型均能在一定程度上减小信号穿墙带来的非视距误差，且修正效果优于SR-WLS 方法。实验中，各次仿真结果中采用未考虑修正的多边测量方法计算出的坐标偏差存在不一致的现象是由锚点与定位节点的相对位置导致。对于图 13 所示误差分布，选取的定位坐标为(-1,11)，结合图10 仿真场景2 可以看出，定位坐标几乎位于BE 垂直平分线与CD 垂直平分线的交点处，这导致获取的各次测距信息的偏差都为同样的趋势，各数据之间的偏差相差并不大，在这种情况下，利用多边测量计算出的定位坐标与实际值的偏差也将较小。因此，坐标求解的误差与锚点和定位节点的摆放位置有一定的关系，但对本文考虑信号穿墙传播的定位模型求解定位坐标并没有太大的影响。

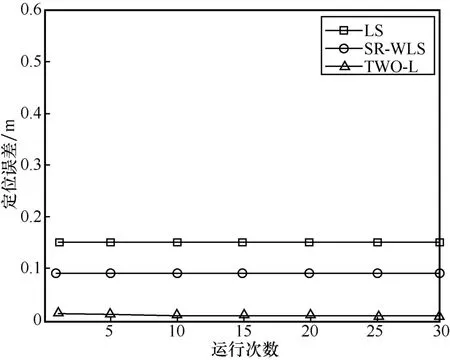
图13 仿真场景2(-1,11)处仿真结果

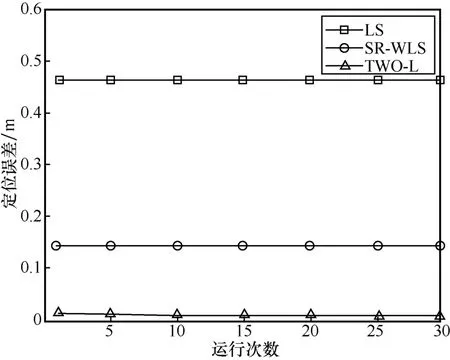
图14 仿真场景2(6,10)处仿真结果

为了验证在室内动态场景下本文方法的适应能力，本节设计了大小为10 m×10 m 的仿真场景，同样选择5 个UWB 节点作为锚点，摆放在墙的一侧，假设墙体厚度d=30cm，相对介电常数ε=4.4 3，在墙的另一侧移动定位节点，进行定点定位，形成一个圆形轨迹，如图15 所示。

图15 室内动态仿真场景

对各定位节点进行仿真测试，分别采用经典最小二乘法、SR-WLS 方法、本文提出的TWO-L 方法计算各定位节点坐标。将各方法计算所得定位节点坐标以及理论坐标绘制成定位节点坐标轨迹，如图16 所示。

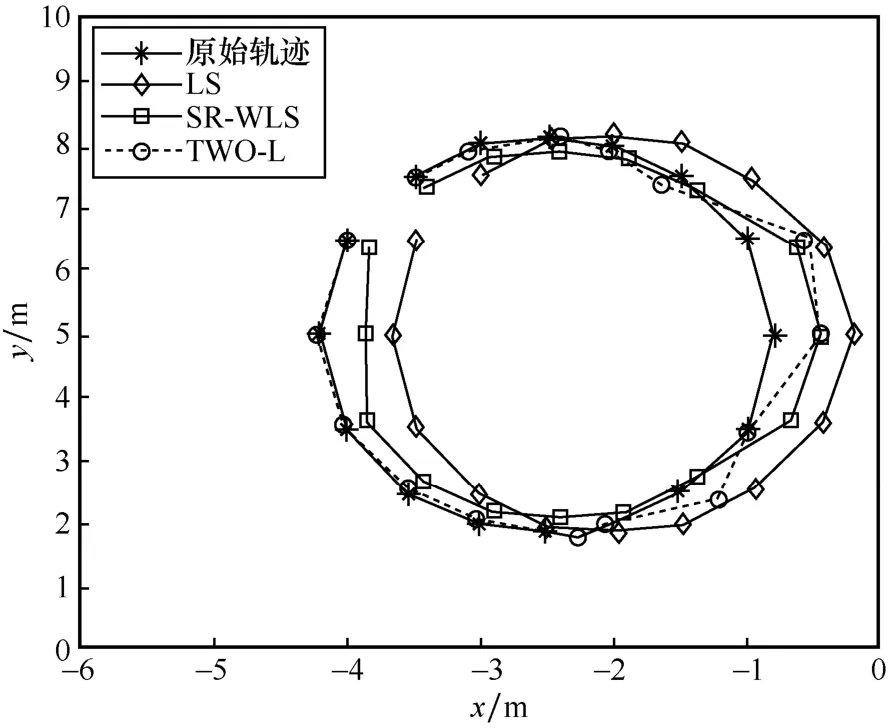
图16 定位节点坐标轨迹

由图16 不难发现，TWO-L 方法与理论坐标拟合得最好，表明了本文模型的有效性。

依据各次仿真实验结果，虽然本文方法对信号穿墙入射角进行了近似，对墙体厚度与介电常数等参数进行了近似处理，但是与未考虑信号穿墙传播模型的最小二乘法以及SR-WLS 方法相比，采用本文方法求解定位坐标仍对定位精度有较大改善。

本文仿真使用的硬件配置为Intel(R) Core(TM)i5-8265U CPU @ 1.60 GHz 1.80 GHz，MATLAB 版本为R2021a，算法开销对比如表2 所示。

表2 算法开销对比

由表2 可知，本文模型虽然较为复杂，但定位算法的开销仍可保证一定的实时性。

4.2 UWB 实测实验

为验证穿墙定位优化模型与实际测量的吻合程度，本文使用如图17 所示的UWB 节点，并在如图18 所示的空心砖墙体隔断的实际室内环境中进行了实测。UWB 节点采用DWM1000 模块DSTWR方式进行测距，经过校准并采用Kalman 滤波算法[25]对多次测量获得的数据进行处理，以减小测距时由多径误差带来的影响。

图17 实验中使用的UWB 节点

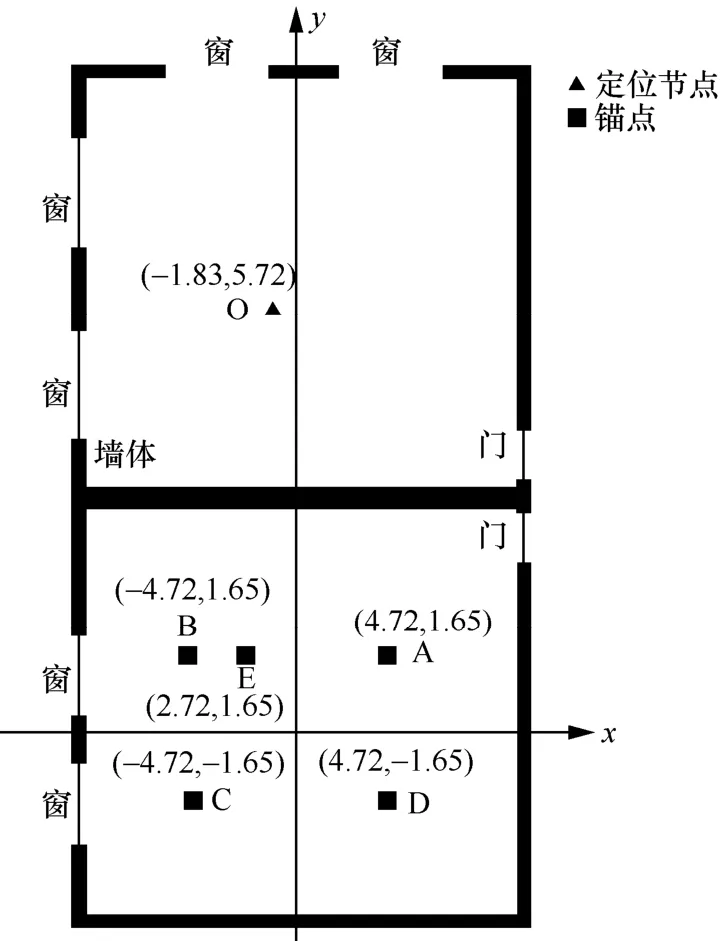
图18 实际室内环境

为与仿真实验相对应，实测实验中，本文利用支架使各节点摆放至同一水平面。

将定位节点置于坐标(-1.83,5.72)处进行测距实验，通过UWB 获取90 次连续测距数据，分别用本文模型计算各次定位所得坐标值，定位误差分布如图19 所示。

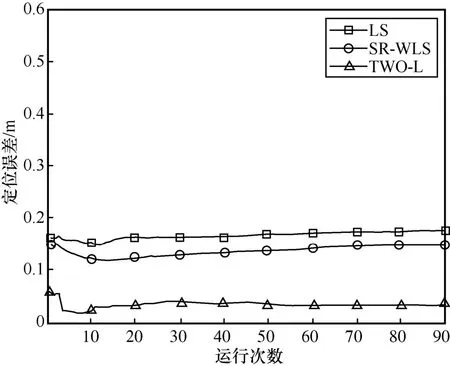
图19 定位节点置于坐标(-1.83,5.72)处的定位误差分布

由图19 可知，实验结果与仿真结果相近，说明考虑信号穿墙传播的定位模型能较好地减小信号穿墙非视距误差。未考虑穿墙的定位误差为16 cm 左右，SR-WLS 方法的定位误差为13 cm 左右，本文模型下的定位误差为5 cm 左右。与SR-WLS 方法相比，TWO-L 方法定位精度提高了61.53%。为直观地表示x与y的坐标偏差，图20 进行了相关的误差CDF 分析，x与y的偏差均为3 cm 左右，表明定位结果较准确。

图20 定位节点置于坐标(-1.83,5.72)处的坐标偏差CDF 曲线

在上述实验的基础上，改变节点位置如图21所示，将其中一个锚点移至(1.65,-1.5)，与定位节点保持视距测量。

图21 实验场景示意（改变一个锚点）

将定位节点置于坐标(5.25,0)处进行实验，定位误差分布如图22 所示。

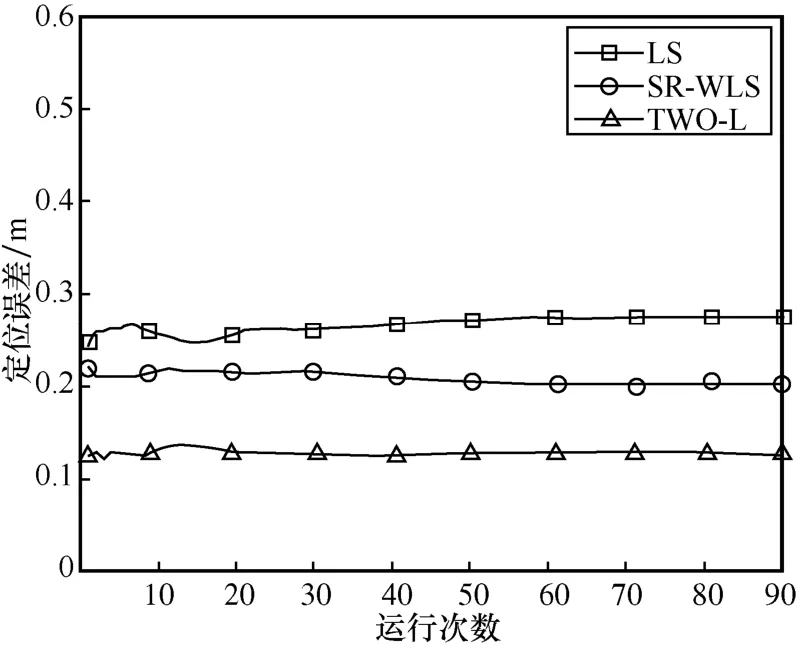
图22 定位节点置于坐标(5.25,0)处的定位误差分布

图22 的实验结果进一步印证了考虑信号穿墙传播的定位模型能较好地减小信号穿墙非视距误差。未考虑穿墙的定位误差为29 cm 左右，SR-WLS方法的定位误差为21 cm 左右，本文模型下的定位误差为13 cm 左右。与SR-WLS 方法相比，TWO-L方法定位精度提高了38.10%。在该实验基础上进行坐标误差累积分析，得到相关的误差CDF 曲线，如图23 所示。

图23 定位节点置于坐标(5.25,0)处的CDF 曲线

图23 所示结果也表明了定位结果的准确性，x坐标偏差约为12 cm，y坐标偏差约为5 cm。

为验证少数锚点与定位节点同时处于非视距测量，而其他锚点为视距测量情形，本文在图21的基础上，改变节点位置，将其中锚点A、B 分别移至(-1.65,0)和(1.65,1)，与定位节点保持视距测量，仅保留2 个锚点与定位节点呈隔墙状态，如图24所示。

图24 实验场景示意（改变2 个锚点）

将定位节点置于坐标(5.25,2)处进行实验，定位误差分布如图25 所示。

由图25 可知，在仅有2 个锚点与定位节点呈隔墙状态下，考虑信号穿墙传播的定位模型也能较好地减小信号穿墙非视距误差。未考虑穿墙的定位误差为45 cm 左右，SR-WLS 方法的定位误差为12 cm左右，本文模型下的定位误差为4 cm 左右。与SR-WLS 方法相比，TWO-L 方法定位精度提高了66.67%。在该实验基础上进行坐标偏差累积分析，得到相关的CDF 曲线如图26 所示。

图26 定位节点置于坐标(5.25,2)处的CDF 曲线

图26 所示结果进一步证明了定位结果的准确性，x坐标偏差接近0，y坐标偏差也仅约为3 cm。总体来说，本文搭建的模型能够较好地修正信号穿墙传播误差，减小非视距影响，提高定位精确度。

5 结束语

针对室内定位中信号穿墙的非视距传播带来的误差问题，本文提出了一种考虑信号穿墙传播结合室内地图推演的定位优化方法。该方法的定位坐标求解不需要已知墙体厚度以及相对介电常数等参数；对于墙体参数不一致的定位环境，在参数间差距较小的情况下，对墙体参数近似一致进行计算对定位结果不会产生显著影响；同时，室内地图推演模型的应用弱化了求解条件，提升了模型对不同测距环境的适应能力。仿真结果表明，与未考虑信号穿墙定位模型相比，本文模型求解得到的定位坐标准确度有较大的提升。基于UWB 的实测实验进一步验证了穿墙定位优化模型的合理性，与仿真实验具有较高的吻合度。本文实验场景下定位精度可显著提高。