集群磁流变抛光加工表面磁轨迹强度建模优化及加工均匀性研究
2023-01-09阎秋生梁智镔潘继生
阎秋生,梁智镔,潘继生
精密与超精密加工
集群磁流变抛光加工表面磁轨迹强度建模优化及加工均匀性研究
阎秋生,梁智镔,潘继生
(广东工业大学 机电工程学院,广州 510006)
探究集群磁流变抛光过程中工艺参数和空间磁场分布特征对加工表面粗糙度不均匀性的影响,通过优化工艺参数,改善加工表面粗糙度的不均匀性。提出一种包含有效加工轨迹和磁轨迹特征的磁轨迹强度数值模型,在数值模型基础上分析转速比、偏心距和往复摆动速度等运动参数对工件不同位置上有效加工轨迹和磁轨迹2种特征的影响,优化不同运动条件下的转速比。在集群磁流变抛光装置上进行硅片的抛光加工实验,利用白光干涉仪检测加工表面粗糙度和表面形貌,总结加工表面粗糙度的分布规律。数值计算结果表明,无理数的转速比能避免出现不同周向位置的周期性波动特征,选用合适的转速比能够减小不同径向位置轨迹长度的差异,提高轨迹特征的均匀性。在无理数转速比条件下,通过改变工件偏心距和增加往复摆动会增大有效加工轨迹的覆盖范围,同时会缩短有效轨迹长度,使得加工效率降低。改变偏心距的运动模式可以改变运动轨迹上磁频数的分布规律,在偏心距为115 mm条件下,工件不同径向位置之间的平均磁场差值可以减小至0.019 T。实验结果表明,通过优化工艺参数后,加工表面粗糙度的变异系数相较于对照组平均下降了约37%。对照组在抛光后的不均匀情况与数值计算结果中的磁轨迹强度径向分布规律相吻合,在小转速比下表现为中心光滑、边缘粗糙的分布规律,在大转速比下表现为边缘光滑、中心粗糙的分布规律。在偏心距为115 mm、转速比为223∶60的优化工艺条件下,抛光硅片的粗糙度变异系数最小达到0.309,平均粗糙度为4.19 nm。对比实验结果与数值模拟结果可知,磁轨迹强度数值模型能有效优化集群磁流变抛光工艺参数,有利于加工轨迹与磁轨迹特征的匹配,改善了工件抛光后的加工不均匀性。
磁流变抛光;数值分析;磁轨迹;表面粗糙度;均匀性
随着半导体技术的应用与发展,对晶片表面的粗糙度、平整度和亚表面损伤等技术要求也越来越高。磁流变抛光作为一种加工力可控的柔性抛光方法,能够在获得纳米级表面粗糙度的同时具有较高效率、无表面损伤的优势,被广泛应用于半导体晶片和光学表面的超精密加工[1-3]。由此,基于磁流变抛光原理发展出了多种用于抛光加工平面的工艺方法,如带式磁流变抛光[4-5]、大抛光模磁流变抛光[6-7]、集群磁流变抛光等[8],相较于传统的轮式磁流变抛光,它通过增大工件加工表面与磁流变抛光介质的接触面积,实现了高效的面域加工。
由于磁场在空间分布的不均匀性,经磁流变抛光后工件表面会出现粗糙度分布不均匀的现象[9-11]。为了实现加工表面粗糙度的一致性,现有研究路线主要有优化运动参数和优化磁场分布。李叶鹏[12]研究了增加工件摆动运动对磁流变抛光加工平整度的影响,结果表明,采用摆动方向为−时,经抛光后工件表面平整度的最高值与最低值的差值PV(Peak Value)最小,加工平整性最好。Luo等[13]建立了分析簇状磁流变的磨料运动轨迹模型,分析了工件装置的运动参数和工件布置形式对轨迹特征的影响。杨杰等[14]研究了定偏心和直线摆动等2种运动方式对轨迹均匀性的影响,结果表明,采用直线摆动加无理数转速比得到的均匀性最好。另一方面,对磁场发生器进行了结构优化设计,改善了梯度磁场在空间中的分布不均的现象,实现了加工的均匀性。Nie等[15]研究了多个圆柱磁极阵列磁通密度分布优化布置,结果表明,采用六边形交叉排列的磁场进行磁流变加工后,工件表面的平面度效果最好,并提出了多个圆柱磁极布置优化的磁轨迹系数评价指标[16]。卢明明等[17]对电磁极磁极头进行了倒角和加工环形槽处理,经优化后梯度磁通密度差异由200 mT减小至80 mT。周琴琴等[18]进行了电磁极发生装置的圆形阵列磁场、扇形磁场和环形磁场数值仿真分析,环形磁场具有较大的有效抛光区域范围,同时满足磁场强度和磁场方向的要求,并在冷却方式上易于实现,是电磁极磁场发生装置的优选方案。
分别研究磁流变抛光运动参数或磁场分布以实现加工均匀性的效果是有限的,因此文中综合集群磁流变平坦化加工过程加工表面运动轨迹与磁场分布强弱变化特征,提出磁轨迹强度模型,用于解决集群磁流变平坦化加工过程的表面粗糙度不均匀性问题。首先依据集群磁流变抛光装置的运动原理和动态磁场变化规律,建立磁轨迹强度理论模型,接着通过数值仿真模拟的方法研究运动参数对运动和磁场特征的影响规律,并优化计算磁轨迹强度的均匀性工艺参数,最后采用优化的工艺参数进行对比实验,分析加工表面的均匀性。
1 集群磁流变平坦化加工
1.1 加工原理
动态磁场集群磁流变平坦化加工装置及原理如图1所示,将1组多个圆柱形永磁极均布在抛光盘内部,并采用偏心机构驱动磁极转动,形成动磁场。抛光工作液中的磁性颗粒沿磁力线形成了磁性链串,约束磨料,构成黏弹性磁流变抛光微磨头,组成了磁流变抛光垫。磨料以半固着状态随机分布在黏弹性抛光垫中,动态磁场的磁力线变化使磁性链串持续重组,以维持抛光垫的活性,保持抛光垫稳定的加工去除能力[11]。在动态磁场集群磁流变平坦化加工过程中,加工表面与抛光盘表面保持一定的间隙,磁流变抛光垫会对加工表面产生法向应力和剪切应力,抛光垫中的磨料对加工表面材料进行塑性微量去除,可以实现表面超精密平坦化加工。
由于集群磁流变平坦化加工的磁极布置间隔性,磁性粒子聚集在磁极上方的磁流变微磨头的面积有限,工件在经过微磨头间的空隙区时存在无效的加工运动轨迹。同时,磁流变微磨头上不同位置的磁通密度不同,当工件在强磁区域被磨料去除时,磨料的去除能力增强。在加工轨迹的占空比和磁场强弱变化等不均匀条件下,加工表面不同位置的表面粗糙度存在差异。
1.2 磁轨迹强度模型
为了研究工件表面加工轨迹与磁场的共同作用,首先需要对工件的平面运动轨迹进行分析。以抛光盘圆心设立笛卡尔坐标系,以工件盘圆心1建立极坐标系,集群磁流变平坦化加工的工件盘运动模型如图2所示。其中,工件盘与抛光盘圆心1之间的距离为偏心距,抛光盘转速为0,工件盘转速为1。当存在往复摆动运动时,工件相对摆动周期为s,摆动距离为[−,+],摆动方向与1之间的角度为摆动角。
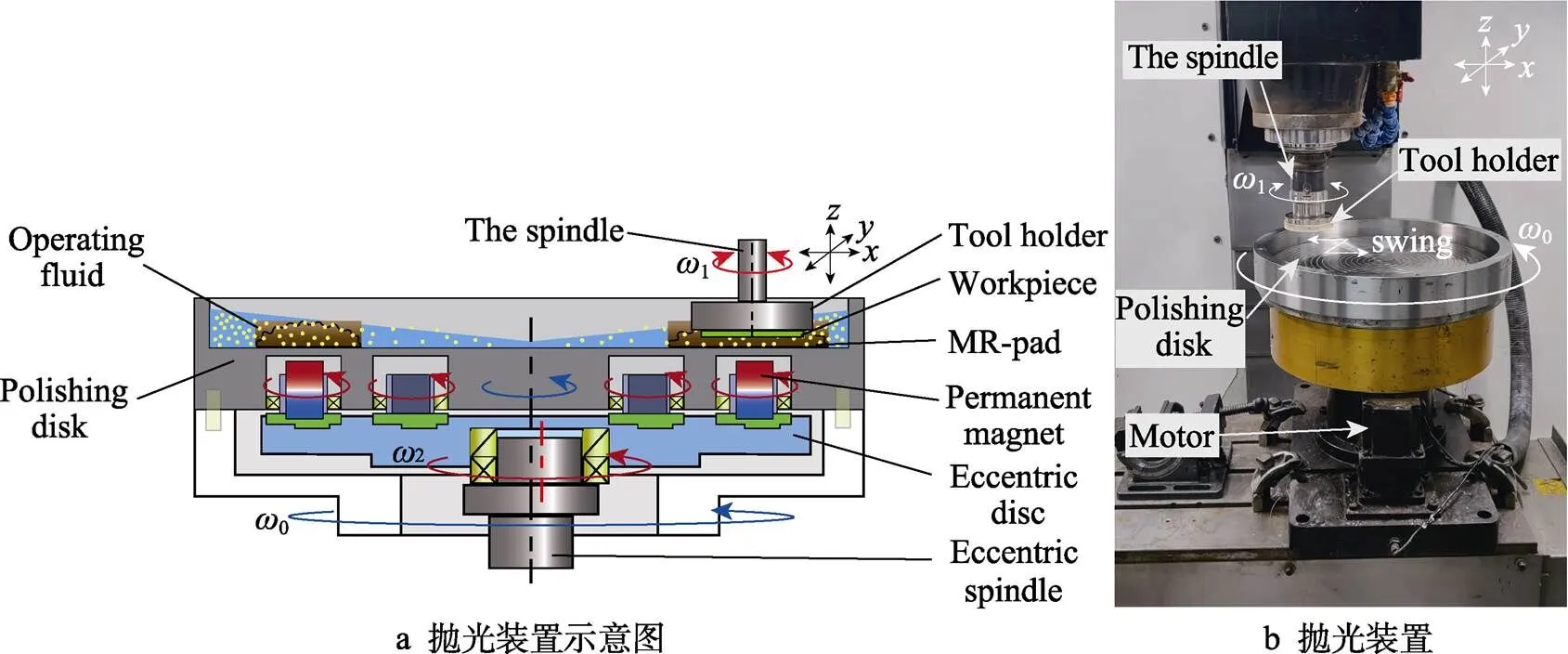
图1 动态磁场集群磁流变平坦化加工实验装置
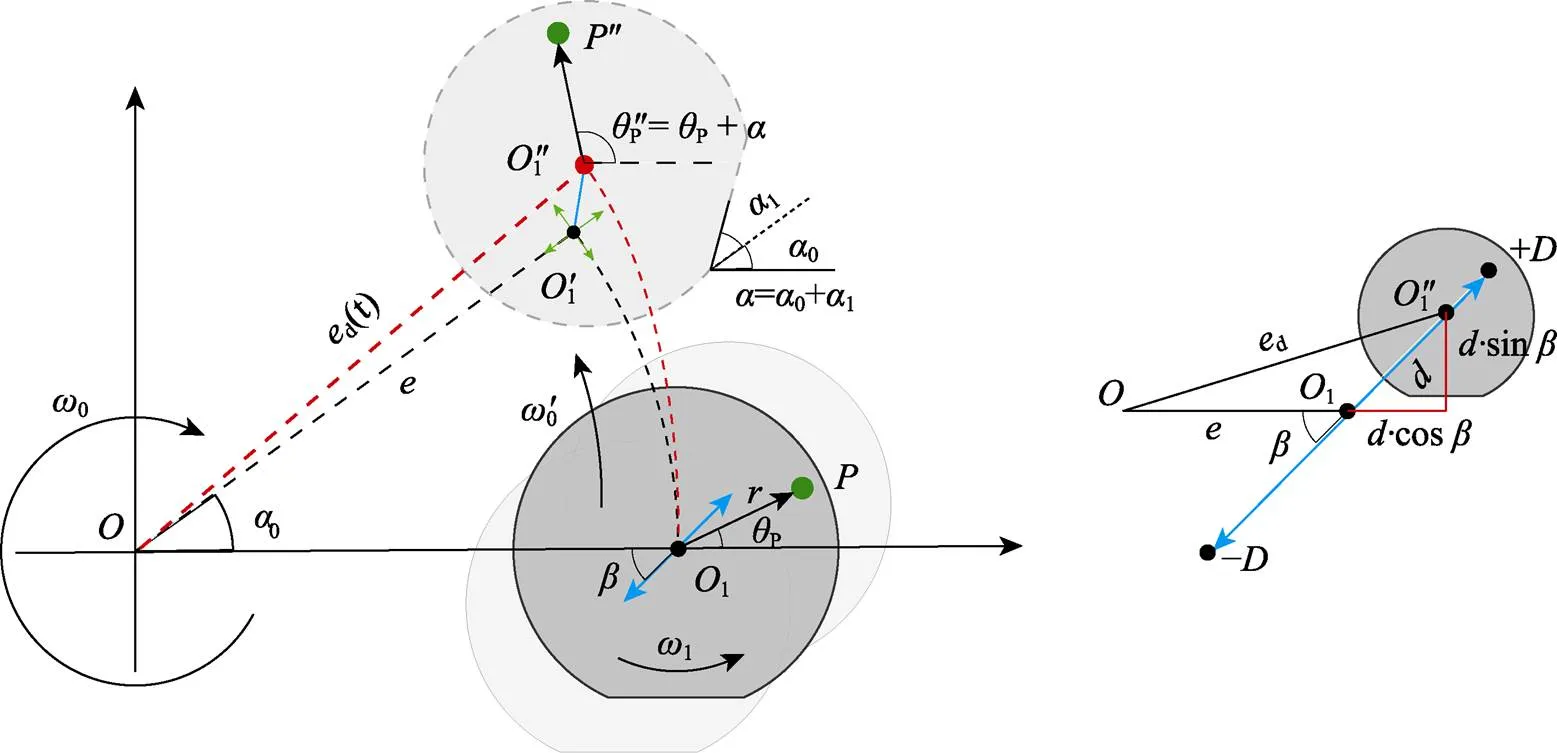
图2 集群磁流变平坦化加工的工件盘平面运动模型
根据上述几何关系和平面运动学原理,工件上任意点(p,p)位置变化的参数方程见式(1)。
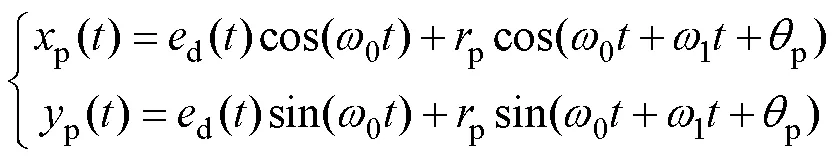
式中:d()是工件偏心距关于时间的参数方程,其变化规律与往复摆动运动参数相关。这里忽略往复运动的加减速阶段,则往复摆动运动可简化成分段匀速直线运动,其参数方程见式(2)—(3)。
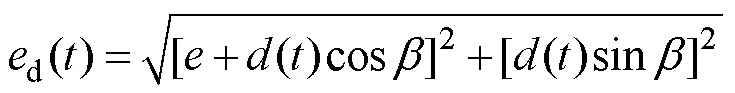
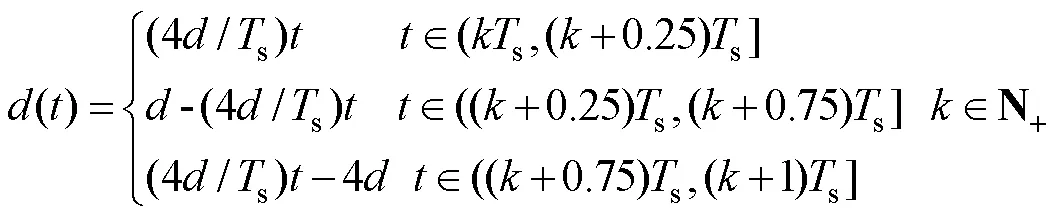
根据速度叠加原则,由位置变化方程式(1)得出了运动速率的变化方程,见式(4)。
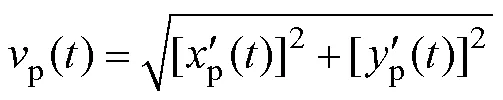
根据磁极的运动规律,求解磁场分布的动态变化过程。在集群磁流变平坦化加工装置中,多个磁极在跟随抛光盘旋以0做旋转运动的同时,每个偏心布置的磁极也绕着各自的轴心2(k)(为磁极序号)以角速度2同步旋转,如图3所示。
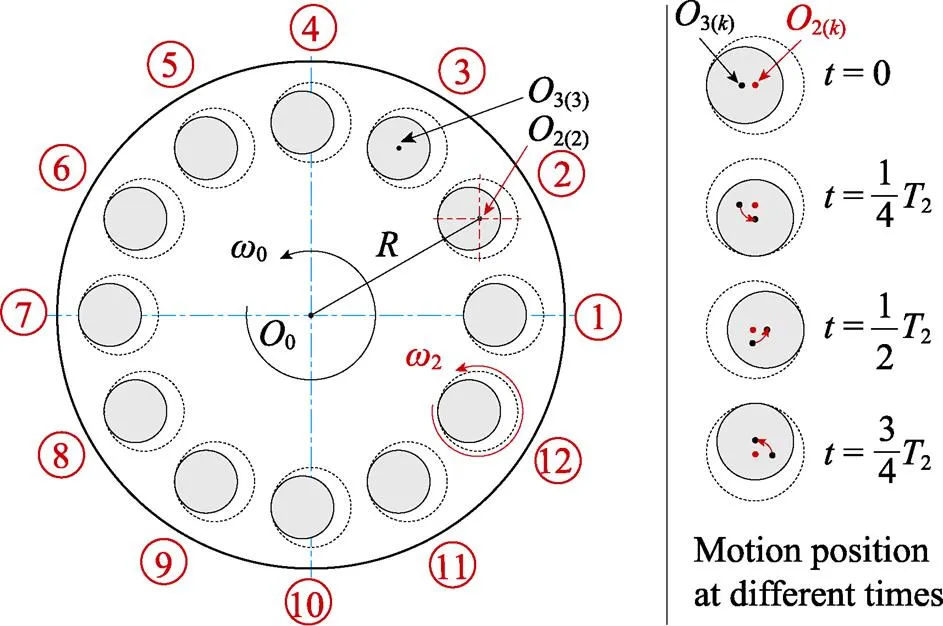
图3 偏心磁极的同步运动示意图
将12个磁极均匀分布在半径=125 mm的圆周上,并以磁极偏心距m=6 mm同步旋转为例,不同序号的磁极对应的旋转轴心2(k)坐标为[125cos(π/12), 125sin(π/12)],圆柱磁极轴心3(k)位置变化的参数方程见式(5)。
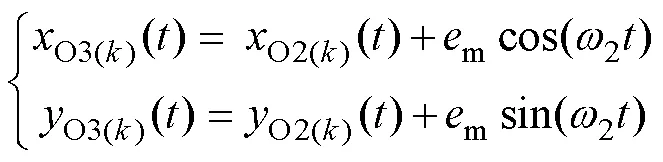
所有磁极轴心同步运动,且初始相位相同,相对位置距离始终一致。由此,可以利用磁极位置相对不变的运动特点,进行12个磁极在磁场仿真求解静态下的磁场分布(,),再根据所有磁极的偏心旋转运动规律对静态磁场进行映射,求解任意时刻=t下的动态磁场分布B(x,y)。坐标i,y的映射变化过程见式(6)。
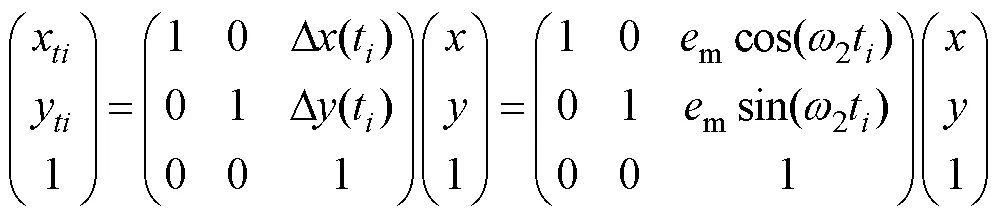
将动点的轨迹位置[p(),p()]带入对应时刻t的动态磁场分布Bi(x,y)中,便得到动点运动轨迹上的磁通密度变化参数方程p(p,p,),即磁轨迹方程,见式(7)。
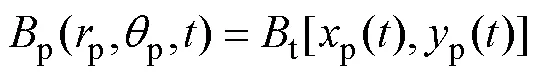
最后,基于磁轨迹强度评估指标表征理论的均匀性。磁流变抛光去除率预测的理论依据为Preston经验公式[19],该公式表明工件的材料去除率与加工速率和应力呈正相关[20]。集群磁流变平坦化加工中的应力包括剪切应力和正应力,这2种应力分布的大小与磁通密度呈正相关[21]。Nie等[16]提出了磁轨迹系数(Coefficient of magnetic trajectory,CMT)的磁场均匀评估方法,用于指导磁场发生装置的优化,磁轨迹系数的定义见式(8)。

式中:为运动时间周期。
为了研究加工轨迹与磁场在加工过程的共同作用,在磁轨迹系数的基础上进一步提出磁轨迹强度模型,以模拟工件加工表面的单点位置在加工过程中的去除量,基本假设如下。
1)将总数一定的磨粒随机分布在集群磁流变抛光垫中,任意区域内存在的磨粒数量与该区域面积呈正相关,服从均匀分布。
2)在均匀分布条件下,任意一段微长度的轨迹经过磨料并发生去除的概率期望相同,轨迹上的总去除频次服从二项分布。
3)当轨迹足够长时,总去除频次正态近似,与磨粒发生作用的有效轨迹长度ep与总去除频次的期望成正比。
4)在材料的去除行为发生时,单次去除量与微端磨料有效轨迹位置上对应的表面磁通密度模呈正相关。
根据以上假设,在时间周期内,工件位置(p,p)上的总材料去除量是轨迹长度变量和磁场强度变量呈正相关的随机值,其期望定义为磁轨迹强度(单位为T·m),见式(9)。
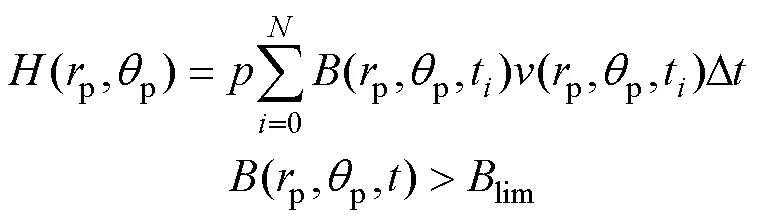
式中:为微段轨迹长度内发生的去除概率;lim为磁流变微磨头边缘处的磁通密度阈值。
磁轨迹强度的定义是数学期望,去除概率对磁轨迹强度的影响是线性的。文中在关注数值的相对差异时,简单取=1。有效加工轨迹是运动轨迹中磁通密度高于阈值lim的磁流变微磨头区域内的部分,如图4所示。
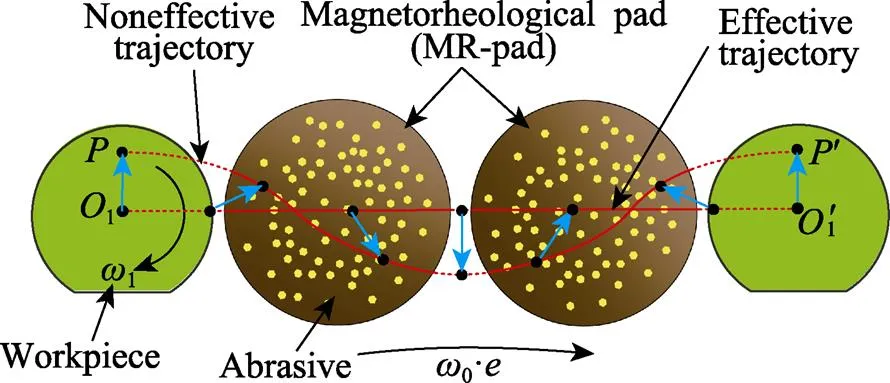
图4 有效加工轨迹示意图
变异系数是一种用于评估数据离散程度的统计学指标,是样本标准差与样本均值的比值,用于表征离散程度的相对性。在数值计算中,以多个位置点的磁轨迹强度变异系数表征去除过程的均匀性,数值越小代表不同位置的去除强度越均匀、越相近,统计指标定义见式(10)。
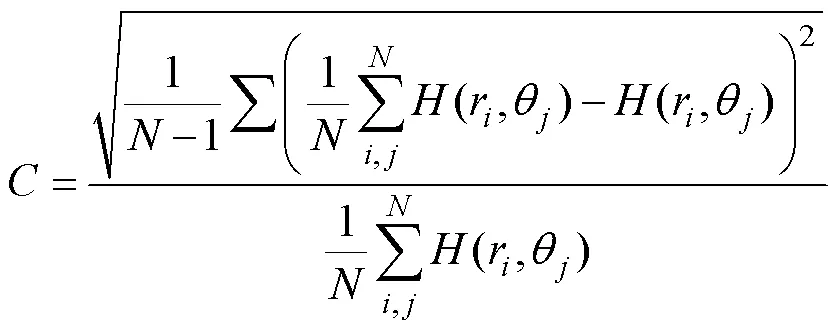
2 有效加工轨迹数值仿真
在集群磁流变平坦化加工过程中,微磨头的非连续性导致工件在加工表面运动过程中径向位置与圆周位置存在不同的运动轨迹特征。探究和分析不同位置的运动特征差异,有利于了解磁轨迹中运动特征对加工不均匀性的影响。
2.1 转速比对磨粒有效轨迹的影响
在平面磨抛运动中,抛光盘与工件转速比=1∶0,它是影响运动轨迹复杂性特征的主要参数[22]。相关研究表明,选用无理数的转速比能够实现永不重复的运动轨迹,可以提高轨迹的均匀性[23-24]。文中根据转速比的类别设置整转速比1/3/7、简单的小数转速比2.4、复杂的小数转速比241∶59(≈4)、无理数转速比π作为有效轨迹仿真的转速比。其中,转速比2.4、3、4与磁极均布数量12存在整倍数关系。设定工件偏心距与磁极圆周分布的半径相同,即工件偏心距=125 mm,抛光盘转速0=60 rad/min,取工件加工表面的一个位置点20(20 mm, 0°),计算运动轨迹在磁流变抛光垫上的有效轨迹长度,不同抛光垫的序号对应图3中的序号排序,结果如图5所示。
由图5a可知,整转速比的轨迹为单条重复轨迹,简单的小数转速比2.4的最小整倍数为5,轨迹循环重复周期为5圈,所以在抛光垫上存在5条轨迹,而复杂的小数转速比241∶59和无理数π的运动轨迹复杂且呈环形包络形状。从图5b可以看出,磨粒加工轨迹的复杂程度能够影响位置点20经过不同磁流变磨头上的磨粒有效加工轨迹长度,复杂的加工轨迹在不同磁流变磨头上的差异小于简单轨迹。不同磁流变微磨头上轨迹长短的不均匀性和周期性变化规律将会影响轨迹的总长度,导致不同位置的去除频次出现较大差别。
由表1可知,在超稀植模式下,对油菜进行覆膜栽培及普通不覆膜栽培,油菜茎粗有较明显的差异,与覆膜对油菜植株高度的影响类似,覆膜稀植油菜较不覆膜种植油菜茎粗在直径上大约2.6 mm。
将计算规模扩大为150×150个栅格化分布点,计算径向位置p=25 mm的有效加工轨迹长度e的分布,其结果以云图形式展现,如图6所示。
通过仿真发现,有效加工轨迹长度的分布表现出2个方向上的差异特征:一种是随着径向位置p变化的径向差异特征;另一种是随着周向位置p变化的周向差异特征,并且主要出现在边缘区域位置。在径向上的数值差异主要与转速比有关,在转速比较小时,中心位置的有效加工轨迹长且边缘短;在转速较大时,边缘位置的有效加工轨迹长度较长,如图6d所示。
周向差异特征与轨迹复杂性和有效加工区域非连续性相关[25]。表现出明显周向差异特征的转速比主要为2.4、3、7,其周向分布上存在周期性波动角度T,T=(/12)2π,其中数值12是非连续加工区域微磨头的均布数量。有理小数转速比241∶59具有较复杂的运动轨迹,但也存在周向差异特征。这是因为该转速比与整转速比4相近,周期性角度T接近2/3π。转速比π在具有复杂运动轨迹的同时,远离了整数值,避免周向位置的加工轨迹长度出现波动现象。
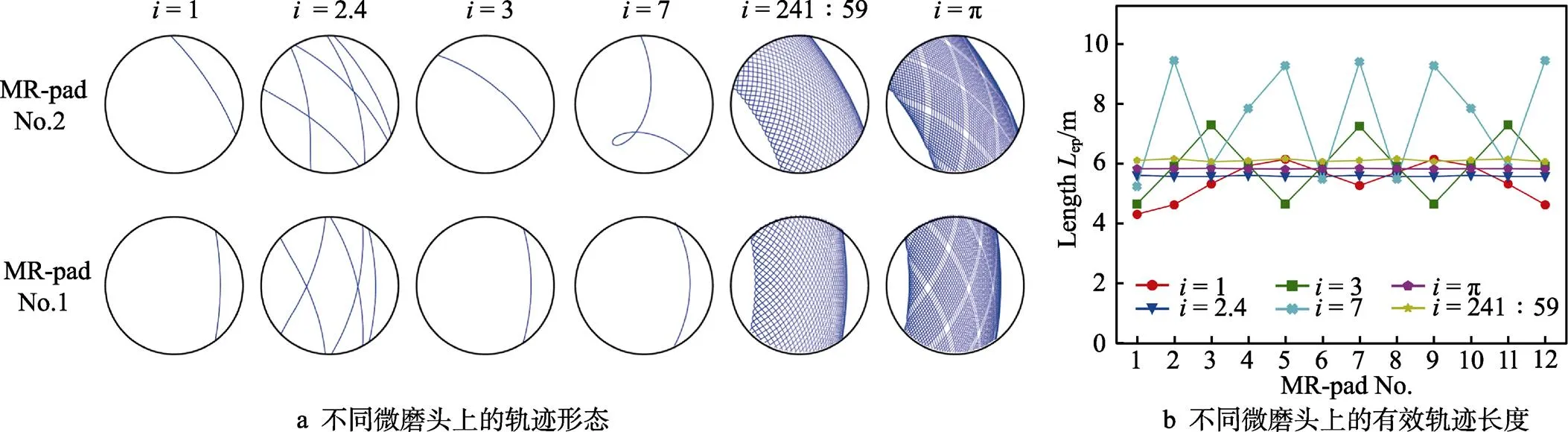
图5 转速比对磨粒有效加工轨迹的影响

图6 磨粒有效加工轨迹长度分布
不同转速比的有效加工轨迹数值分析结果说明,适宜的转速比能够减小工件径向位置的轨迹长度差异,选用无理数和复杂有理小数的转速比能使运动轨迹复杂化,减小工件不同周向位置的轨迹长度差异,提高磁轨迹模型中运动部分的均匀性。
2.2 工件偏心距对有效加工轨迹的影响
工件偏心距的变化能够改变工件有效加工轨迹与磁流变抛光垫的相对位置,同时影响轨迹特征和磁场分布特征。设定偏心距=125 mm,变位偏心距=135 mm。设定摆动运动参数,摆动周期s=2.5 s,摆动距离=10 mm,摆动角度为0°、45°、90°。计算10(10 mm, 0°)在无理数转速比π时增加往复运动的有效加工轨迹形态,其结果如图7所示。
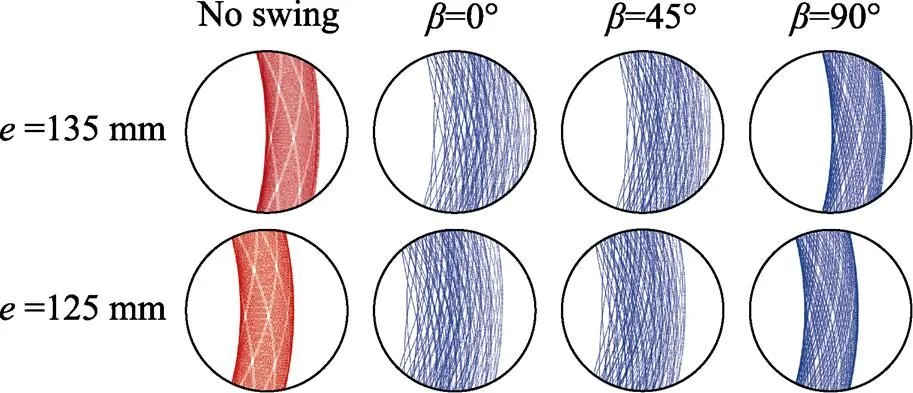
图7 工件不同偏心距和摆动角度的有效加工轨迹形态
通过改变工件偏心距能调整工件相对磁流变磨头的位置及磨料轨迹形态,增加往复摆动则会增加轨迹覆盖范围,在一定程度上也增加了轨迹的重复周期和复杂性。往复运动的角度越小,轨迹的变化范围越大。这是因为增大摆动角度会导致偏心距变位距离减小,见式(2)。
为了探究摆动距离对周向差异的影响,采用=0°的往复摆动和整转速比3,设定不同往复运动距离和摆动周期s,计算工件在p=20 mm处不同周向位置的有效加工轨迹长度,结果如图8所示。
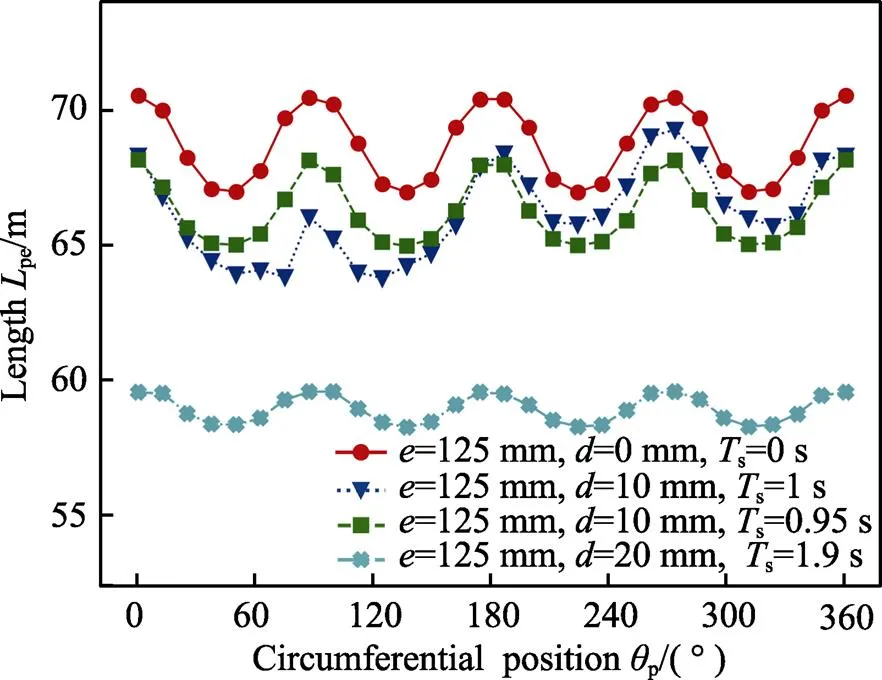
图8 工件在不同摆动运动下的有效加工轨迹长度
由图8可知,在增加工件往复摆动运动后,不同周向位置的有效轨迹长度波动差异减小,但随着周向角度p的变化,周期性波动现象未被消除。当往复摆动参数采用简单的整数摆动周期s=1 s时,工件上(20, 90°)和(20, 270°)位置上的差异增大,采用小数周期s=0.95 s时则不存在该状况,说明摆动周期s与转速比一样,采用小数周期有利于增加轨迹的复杂性,而简单的周期特性会增加局部位置的占空比,致使部分位置的有效轨迹长度变短或变长。增大摆动距离至=20 mm后,轨迹长度的相对波动幅度减小,周向差异特征减弱。同时,工件相对微磨头中心位置的偏离值更大,有效接触面积大大降低,有效加工轨迹长度降低,这影响了整体的去除效率。
3 磁轨迹数值仿真分析
3.1 磁通密度仿真分析
基于动态磁场分布建立磁轨迹方程,动态磁场需要通过静态磁场映射变化得出,因此首先需要通过仿真软件求解静态的磁场分布(,)。通过COMSOL仿真软件进行静态磁场分布求解,简略的仿真步骤:对加工装置建立实体模型,12个相邻磁极以N−S极交互朝上的形式排布在=125 mm的圆周位置上,在磁极上方3 mm处存在直径disk=180 mm、厚度=4 mm的抛光盘。在抛光盘上形成了12个处于挤压状态的直径pad=60 mm、高度=1 mm的磁流变黏弹性磨头,磁极到抛光垫挤压面的总距离为8 mm,如图9a所示。设置磁极材料为N52钕铁硼,剩磁强度为1.48 T,磁流变黏弹性磨头的相对磁导率为8,不锈钢抛光盘与空气部分的相对磁导率为1。将几何模型划分为自由四面体网格后进行有限元求解,通过后处理获取磁流变黏弹性磨头表面高度平面上的磁场感应强度分布,结果如图9b所示。将数据导出后在Python编程软件中按照式(6)进行映射变换,最终获得动态磁场分布t(t,t)。
3.2 磁轨迹数值分析
由上述分析可知,选用无理数的转速比可以大幅减小工件上周向分布特征的差异,因此径向位置p的运动特征分布对均匀性的影响更为关键。当采用无理数的转速比使轨迹足够复杂化时,可以忽略工件的周向位置p,因此只对径向位置p进行数值模拟计算,在保证计算精度的同时大幅减少了计算量。同时,在实际加工过程中装置的运动精度也不可能完全保证整转速比,微小的数值偏离和足够长的加工时间会让轨迹复杂化。
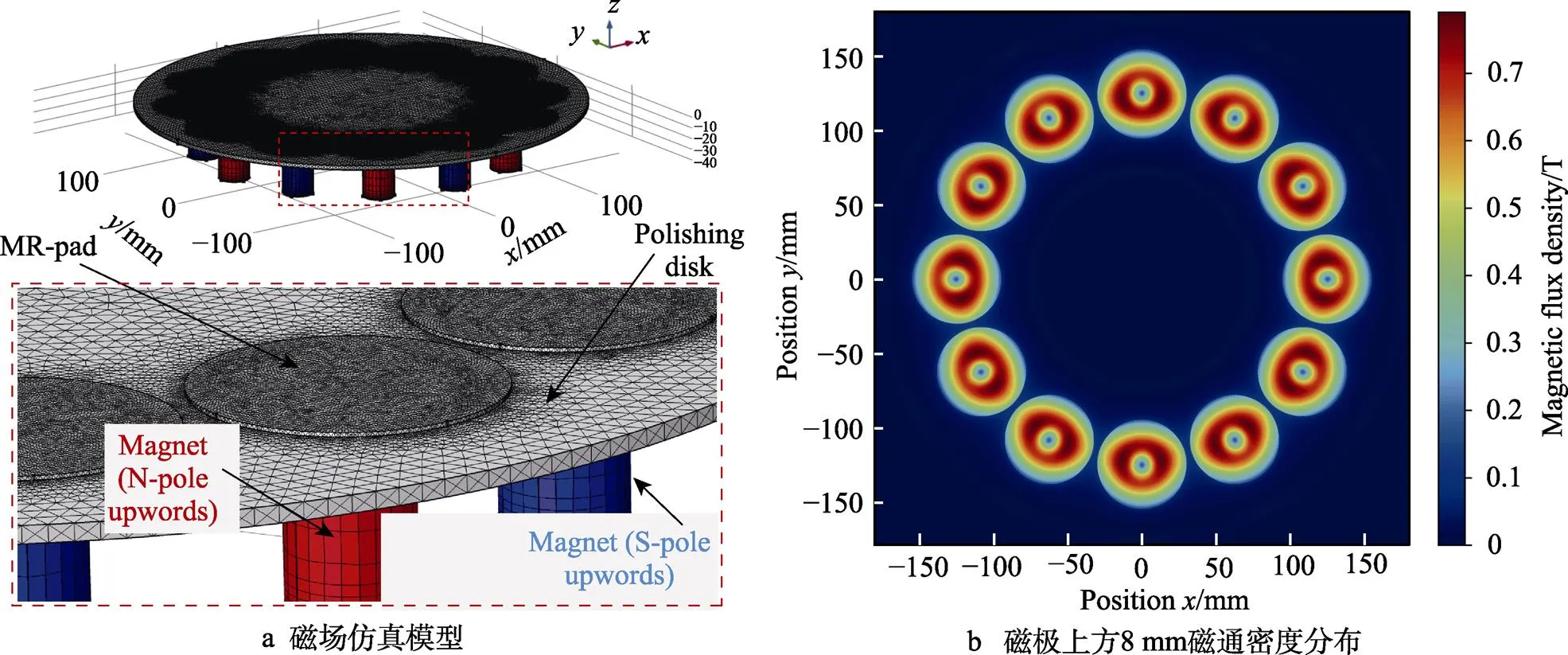
图9 磁通密度仿真
根据偏心距的变化规律,可将加工过程中的运动模式分为定偏心距和变偏心距运动,选取无理转速比π,计算工件上多个径向位置在运动周期=100 s后的有效轨迹上的磁场分布频数,并以小提琴图的形式绘制,如图10所示。
在定位偏心距=125 mm的模式下,中心位置轨迹在强磁区域的频数相对较高,而边缘位置经过强磁和弱磁区域的频数较均衡,2个位置的平均磁场差异为0.079 T。在增加=10 mm往复摆动后,各位置的磁场频数分布规律变化不大,但中心和边缘位置的平均值差异减小。采用偏心距=115 mm时,频数分布规律发生了变化,不同径向位置之间的平均值差异进一步减小至0.019 T,同时最低平均强度的位置由p=24 mm转移至p=16 mm。由此可知,偏摆运动和偏心距变位能够改变轨迹与微磨头的相对位置,从而调整不同径向位置轨迹上的磁场分布特征,使不同位置的磁场特征差异减小。

图10 不同径向位置的磁通密度频数分布
3.3 磁轨迹强度计算与工艺优化
通过对磁轨迹强度的运动特征和磁场特征的研究可知,运动模式对这2种不均匀特征都会产生影响。根据工件偏心距的大小和运动划分为3种方式,分别为定偏心距=125 mm、偏心距变位=115 mm和增加往复摆动的变偏心距=(125±10) mm,将转速比作为数值优化的自变量,对多个工件不同径向位置的磁轨迹强度和变异系数进行了数值计算,结果如图11所示。
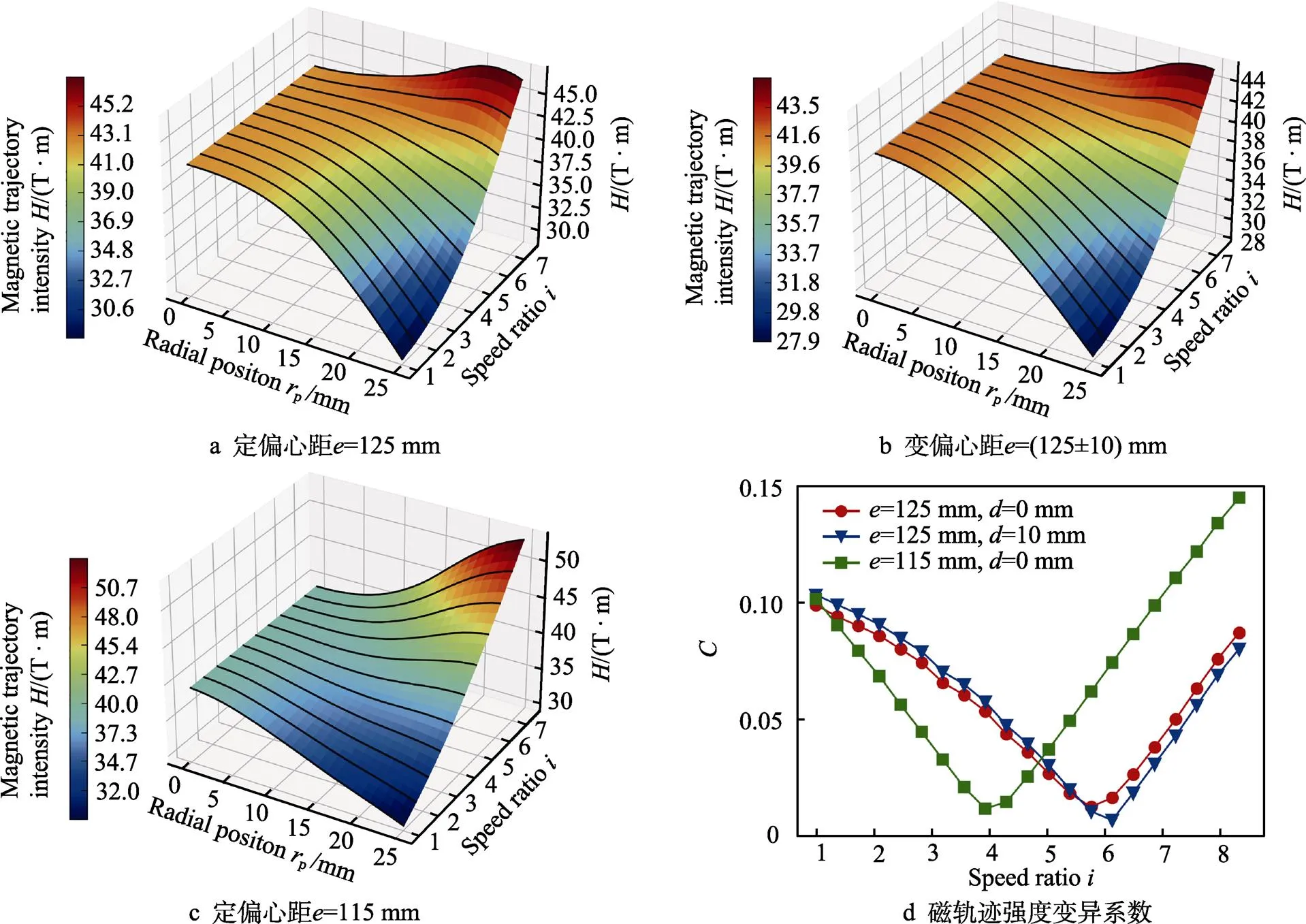
图11 不同转速比的磁轨迹强度和变异系数
随着转速比的增大,工件径向位置的磁轨迹强度分布特征由中心强、边缘弱逐渐变成边缘强、中心弱,磁轨迹强度的变异系数也呈现先降后升的趋势。由图11d可见,不同运动模式的优选转速比区间不同,当转速比数值对应于合适范围时,轨迹特征和磁场特征强弱互补达到平衡的效果最好,磁轨迹强度变异系数最小。由上述分析可知,转速比采用偏心距=115 mm时磁场差异较小,因此优选的转速比数值范围也相对较小。在不同运动模式下计算的优选转速比如表1所示。
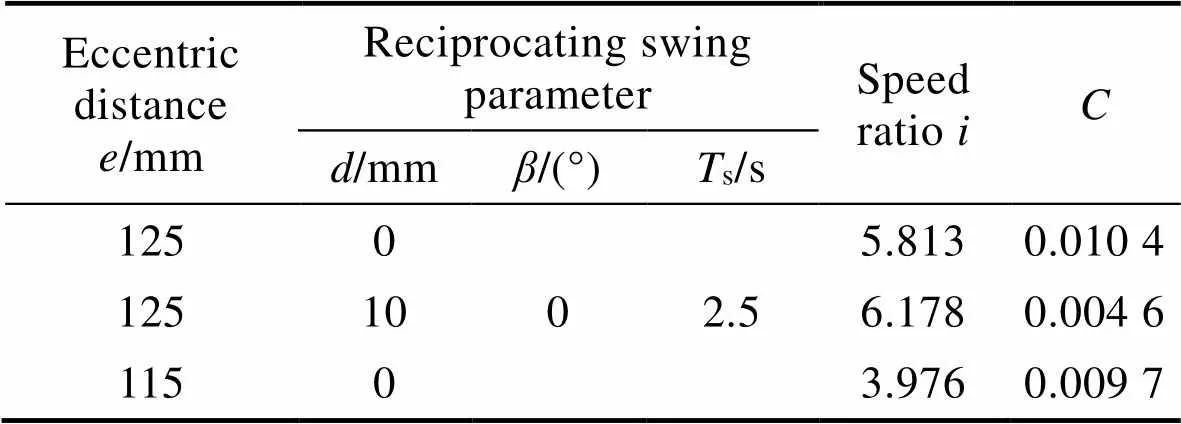
表1 不同运动模式的优选转速比
4 集群磁流变平坦化加工实验及其结果分析
4.1 实验设计
为了更直观体现加工后工件表面不同位置的粗糙度差异,选用2寸硅片作为试件进行集群磁流变平坦化加工,硅片的初始表面粗糙度平均值为0.35 μm。磁流变工作液配方:粒径W3羰基铁粉(质量分数15%)、粒径W1的金刚石磨料(质量分数2%)、去离子水(质量分数80%),其余为少量添加剂(包含分散剂、防锈剂和消泡剂等)。实验在动态磁场集群磁流变平坦化加工实验装置上进行。
实验分为A组、B组(见表2),对照A组在定偏心距=125 mm下选用较大或较小转速比(18、0.33、−1),便于观察粗糙度分布的规律。其中,转速比为−1代表抛光盘转速0与工件盘转速1的大小相同,但旋转方向相反。在运动参数0=−1时,式(1)的类摆线轨迹方程退化成偏心圆轨迹方程,工件上不同位置的运动轨迹长度相等,但边缘的有效轨迹长度最短。B组分别选择定偏心距=125 mm、=115 mm和变偏心距=(125±10) mm等3种运动方式的理论优化工艺参数,其余工艺参数:加工间隙为1 mm、磁极转速2=60 rad/min、摆动角度=0°、摆动周期s=2.5 s、加工时间为120 min。
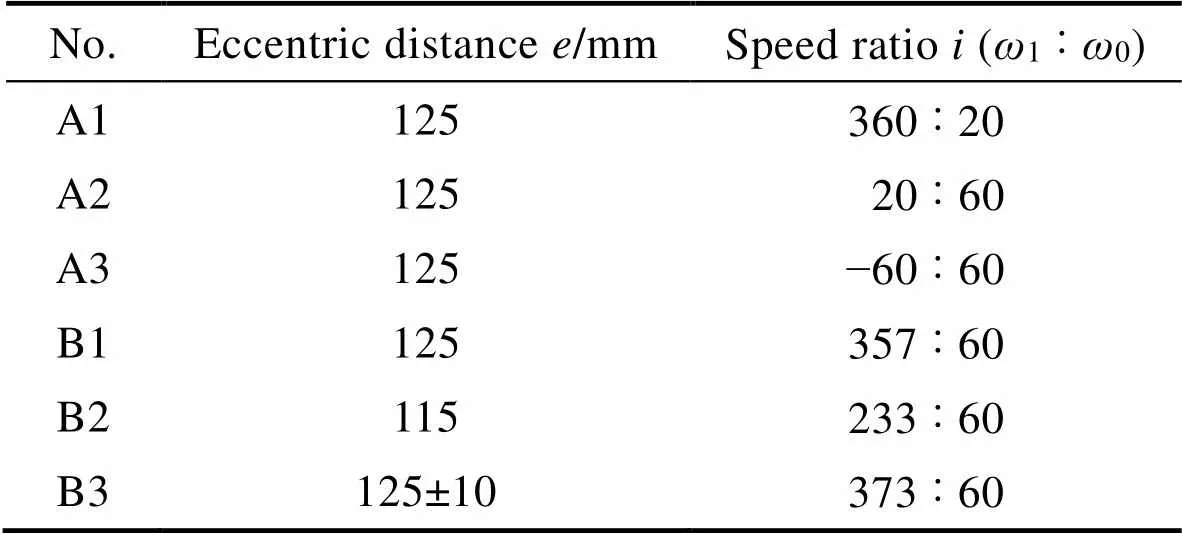
表2 实验分组与参数
4.2 检测评估方法
磁轨迹强度模型评估了不同位置的去除强弱能力,而去除强弱的差异会造成加工后工件表面粗糙度的不均匀分布,可以通过粗糙度的分布间接评估加工均匀性。采用布鲁克GT−X3白光干涉仪检测硅片加工表面上多点的表面粗糙度,采样点范围为120 μm× 94 μm,将采样点尽可能均匀地分布在晶片表面,15个采样点的粗糙度如图12所示。计算所有样本的粗糙度变异系数c,以评估加工后的表面粗糙度均匀性。
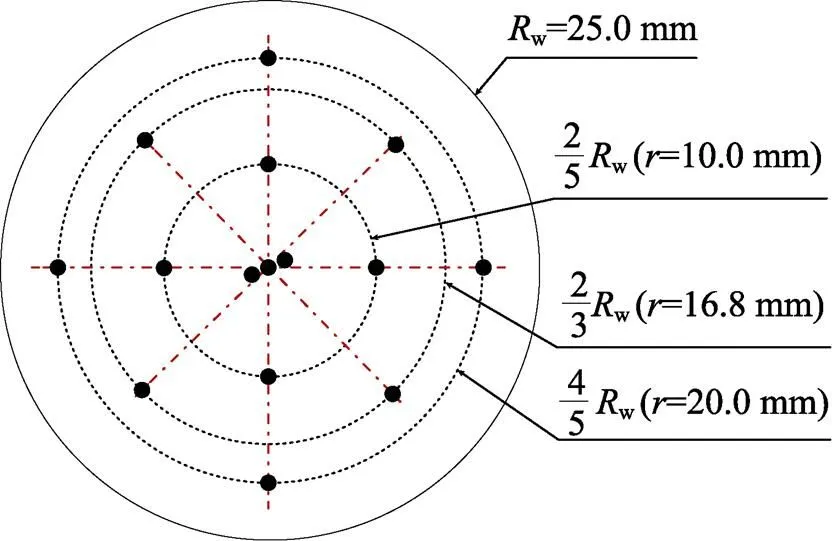
图12 晶片表面粗糙度检测点分布
4.3 加工表面粗糙度及其均匀性
在集群磁流变平坦化加工后多点粗糙度的统计结果如图13所示。A组、B组的变异系数平均值分别为0.746和0.458,B组的变异系数相较于A组平均减小0.288,下降了约38.6%,说明B组工艺的抛光均匀效果优于A组,可见采用优化的工艺参数有利于提高表面质量的均匀性。在偏心距=115 mm、转速比=3.84的无摆动运动工艺下的变异系数最小值为0.309,均匀性最优,同时其平均粗糙度也较好。
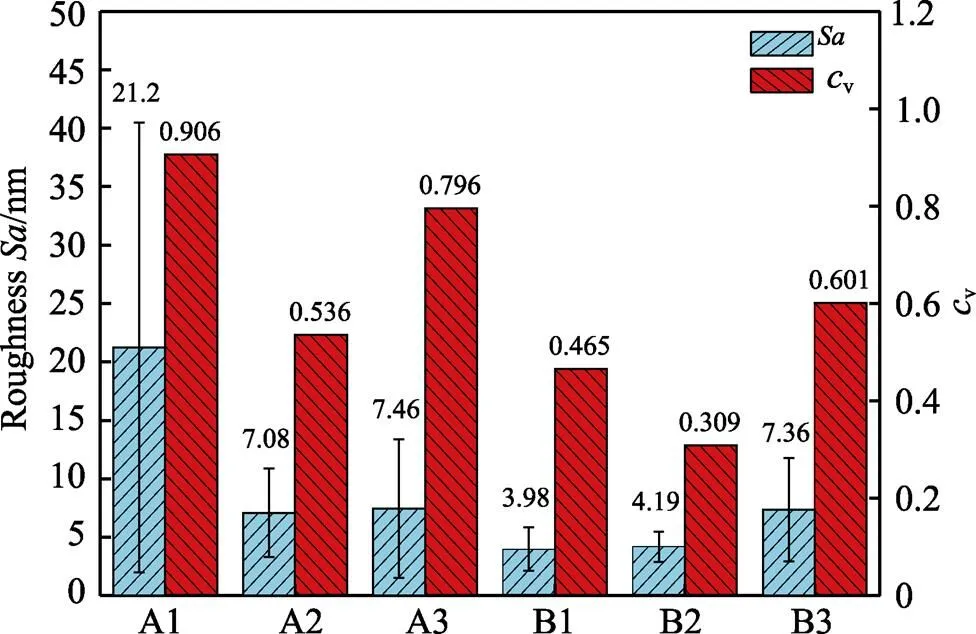
图13 不同实验组试件加工表面粗糙度和变异系数
加工后平均表面粗糙度在径向位置上的分布规律如图14所示。采用大转速比的A1组呈现出中心粗糙、边缘光滑的径向分布规律,采用小转速比的A2组和A3组则与A1组的情况相反,呈现出中心光滑、边缘粗糙的规律。这说明过大或过小的转速比均不利于轨迹长度与磁通密度的匹配,导致径向位置的去除能力差异增大,加工均匀性较差。A3组边缘位置的轨迹长度在理论上短于A2组的,因此在相同公转速度下两者的中心位置的粗糙度基本一致,但在边缘位置上A3组的粗糙度更高,这符合理论预期。均匀组B1和B2在径向位置上的粗糙度分布变化较小。均匀组B3中的平均粗糙度和变异系数较大,其原因可能是过高的自转速度导致磨料在离心力作用下逃逸出抛光垫区域,导致粗糙度整体提高。同时在小转速比下抛光具有运动速率波动小、运动轨迹曲率变化不明显等特点[26],这有利于加工的均匀性。
4.4 加工表面形貌特征
在定偏心距=125 mm运动条件下,抛光后A1组和B1组在不同位置上的表面形貌如图15所示。由于试件的初始表面粗糙度较大,亚表面损伤层较深,在加工120 min后其表面存在较多的坑洞缺陷。去除能力越强的位置,其表面形貌中的坑洞缺陷数量较少,深度也较低。可以看出,由于对照A1组的转速比较大,其边缘位置的磁轨迹更强,因此边缘区域相对于中心区域的去除能力更强,粗糙度相对较低,同时其最大深度相对于中心位置更小。选用合适转速比的B1组仍然存在一定的径向差异,但整体的粗糙度均匀程度相较于A1组得到明显改善。
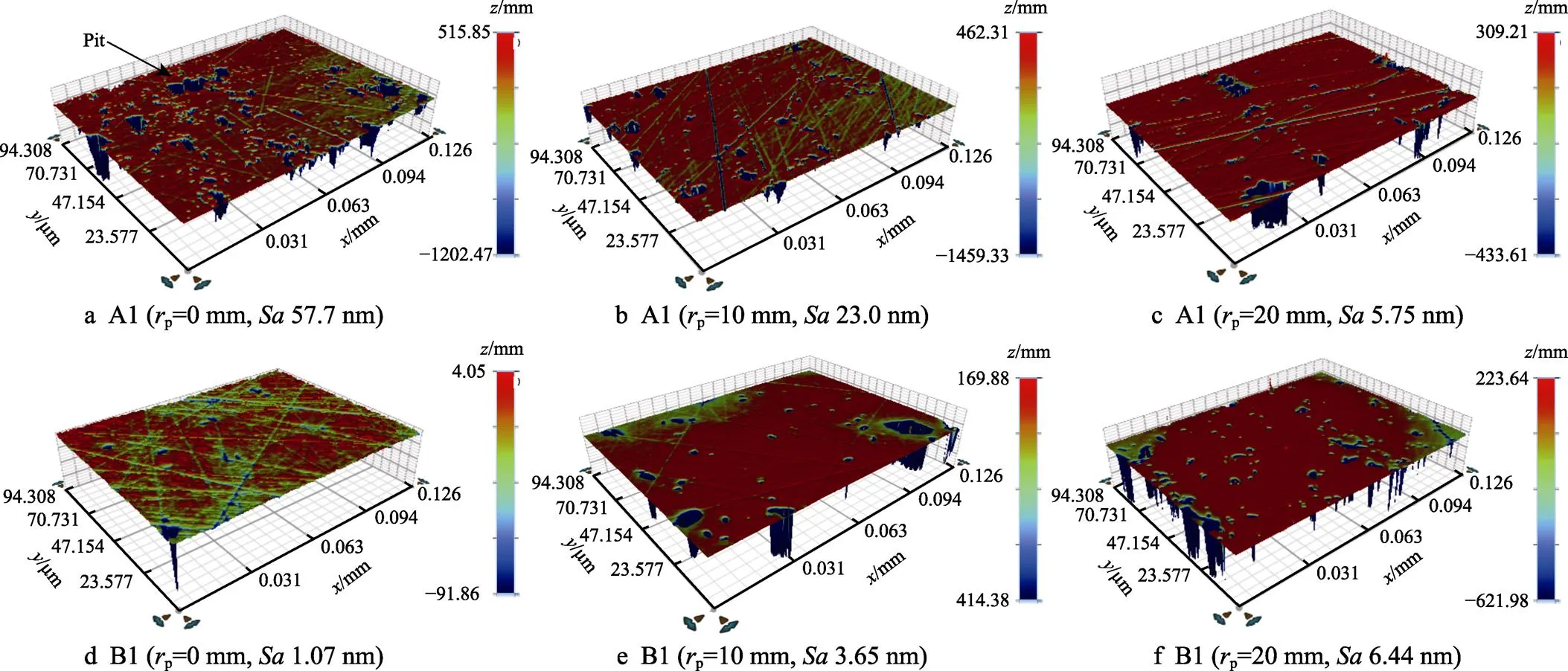
图15 试件加工后不同径向位置表面形貌
5 结论
1)通过集群磁流变加工运动轨迹的数值分析发现,对于存在非连续有效加工区域的集群磁流变平坦化加工,工件与抛光盘的转速比是实现运动均匀的关键参数。选择合适的转速比能够减小工件径向位置的加工轨迹长度差异,选择无理数和复杂有理小数的转速比能够增加轨迹的复杂性,减小周向位置上的轨迹长度差异。
2)通过磁轨迹强度数值分析发现,在工件与抛光盘的偏心距为125 mm时,中心位置的平均磁通密度强于边缘区域,不同的工件偏心距和偏摆运动距离会改变磁场强弱的频数分布。通过优化工件与抛光盘转速比等参数能够使加工表面不同位置的轨迹长度和磁场特征匹配互补,使得加工表面整体磁轨迹强度的变异系数较小,有利于实现加工表面粗糙度的均匀化。
3)以单晶Si片为试件在集群磁流变平坦化加工实验装置上进行加工实验,采用建模仿真优化工艺参数,加工后得到的表面粗糙度变异系数相对于对照组下降了约38.6%,加工表面粗糙度在硅片径向分布均匀性得到有效改善,中心与边缘区域的相对差异大幅减小,加工表面粗糙度均匀化效果明显。
[1] JAIN V K. Magnetic Field Assisted Abrasive Based Micro-/Nano-Finishing[J]. Journal of Materials Processing Technology, 2009, 209(20): 6022-6038.
[2] XU Jin-huan, LI Jian-yong, CAO Jian-guo. Effects of Fumed Silica Weight Fraction on Rheological Properties of Magnetorheological Polishing Fluids[J]. Colloid and Polymer Science, 2018, 296(7): 1145-1156.
[3] 侯晶, 王洪祥, 陈贤华, 等. 大口径平面光学元件的磁流变加工[J]. 光学精密工程, 2016, 24(12): 3054-3060.
HOU Jing, WANG Hong-xiang, CHEN Xian-hua, et al. Magnetorheological Processing for Large Aperture Plane Optical Elements[J]. Optics and Precision Engineering, 2016, 24(12): 3054-3060.
[4] WANG D, HU H, LI L, et al. Effects of the Gap Slope on the Distribution of Removal Rate in Belt-MRF[J]. Optics Express, 2017, 25(22): 26600-26614.
[5] 王德康. 带式磁流变抛光关键技术研究[D]. 北京: 中国科学院大学(中国科学院长春光学精密机械与物理研究所), 2018: 19-20.
WANG De-kang. Study on the Key Technologies of Belt Magnetorheological Finishing[D]. Beijing: Institute of Physics, Chinese Academy of Sciences, 2018: 19-20.
[6] WANG Y Q, YIN S H, HUANG H, et al. Magnetorheological Polishing Using a Permanent Magnetic Yoke with Straight Air Gap for Ultra-Smooth Surface Planarization[J]. Precision Engineering, 2015, 40: 309-317.
[7] 尹韶辉, 邓子默, 郭源帆, 等. 单晶碳化硅的电磁场励磁大抛光模磁流变抛光[J]. 表面技术, 2020, 49(10): 309-315.
YIN Shao-hui, DENG Zi-mo, GUO Yuan-fan, et al. Magnetorheological Polishing Using Large Polishing Tool Excited by Electromagnetic Field for Silicon Carbide Wafer[J]. Surface Technology, 2020, 49(10): 309-315.
[8] 潘继生, 阎秋生, 路家斌, 等. 集群磁流变平面抛光加工技术[J]. 机械工程学报, 2014, 50(1): 205-212.
PAN Ji-sheng, YAN Qiu-sheng, LU Jia-bin, et al. Cluster Magnetorheological Effect Plane Polishing Technology[J]. Journal of Mechanical Engineering, 2014, 50(1): 205-212.
[9] GHOSH G, DALABEHERA R K, SIDPARA A. Parametric Study on Influence Function in Magnetorheological Finishing of Single Crystal Silicon[J]. The International Journal of Advanced Manufacturing Technology, 2019, 100(5): 1043-1054.
[10] PAN Ji-sheng, YU Peng, YAN Qiu-sheng, et al. An Experimental Analysis of Strontium Titanate Ceramic Substrates Polished by Magnetorheological Finishing with Dynamic Magnetic Fields Formed by Rotating Magnetic Poles[J]. Smart Materials and Structures, 2017, 26(5): 055017.
[11] GUO Hui-ru, WU Yong-bo, LU Dong, et al. Effects of Pressure and Shear Stress on Material Removal Rate in Ultra-Fine Polishing of Optical Glass with Magnetic Compound Fluid Slurry[J]. Journal of Materials Processing Technology, 2014, 214(11): 2759-2769.
[12] 李叶鹏. 直线摆动方式磁流变平整加工工艺研究[D]. 长沙: 湖南大学, 2016: 30-32.
LI Ye-peng. Research of Magnetorheological Planarization Technology Based on Linear Oscillation[D]. Changsha: Hunan University, 2016: 30-32.
[13] LUO Bin, YAN Qiu-sheng, PAN Ji-sheng, et al. Uniformity of Cluster Magnetorheological Finishing with Dynamic Magnetic Fields Formed by Multi-Magnetic Rotating Poles Based on the Cluster Principle[J]. The International Journal of Advanced Manufacturing Technology, 2020, 107(1): 919-934.
[14] 杨杰, 洪滔, 文东辉, 等. 研磨驱动方式和转速比对磨粒运动轨迹的影响研究[J]. 机电工程, 2018, 35(5): 453-458.
YANG Jie, HONG Tao, WEN Dong-hui, et al. Influence of Lapping Drive Mode and Rotational Speed Ratio on the Track of Abrasive Particles[J]. Journal of Mechanical & Electrical Engineering, 2018, 35(5): 453-458.
[15] NIE Meng, CAO Jian-guo, LI Jian-yong, et al. Magnet Arrangements in a Magnetic Field Generator for Magnetorheological Finishing[J]. International Journal of Mechanical Sciences, 2019, 161/162: 105018.
[16] NIE Meng, CAO Jian-guo, LIU Yue-ming, et al. Influence of Magnets' Phyllotactic Arrangement in Cluster Magnetorheological Effect Finishing Process[J]. The International Journal of Advanced Manufacturing Technology, 2018, 99(5): 1699-1712.
[17] 卢明明, 庄绪龙, 周家康, 等. 集群磁流变磁场分布模型与优化设计[J]. 制造技术与机床, 2021(10): 45-49.
LU Ming-ming, ZHUANG Xu-long, ZHOU Jia-kang, et al. Distribution Model and Optimization Design of Cluster Magnetorheological Field[J]. Manufacturing Technology & Machine Tool, 2021(10): 45-49.
[18] 周琴琴, 彭可, 陈永福, 等. 磁流变抛光加工中磁场发生装置的设计与实验[J]. 表面技术, 2020, 49(6): 337-344.
ZHOU Qin-qin, PENG Ke, CHEN Yong-fu, et al. Design and Experiment of Magnetic Field Generator in Magnetorheological Polishing Process[J]. Surface Technology, 2020, 49(6): 337-344.
[19] KORDONSKI W, GORODKIN S. Material Removal in Magnetorheological Finishing of Optics[J]. Applied Optics, 2011, 50(14): 1984-1994.
[20] ZHANG Feng. Research Progress of Magnetorheological Finishing Technology at CIOMP[J]. Laser & Optoelectronics Progress, 2015, 52(9): 092202.
[21] LIU Jia-bao, LI Xiao-yuan, ZHANG Yun-fei, et al. Predicting the Material Removal Rate (MRR) in Surface Magnetorheological Finishing (MRF) Based on the Synergistic Effect of Pressure and Shear Stress[J]. Applied Surface Science, 2020, 504: 144492.
[22] WEN Dong-hui, QI Huan, MA Li, et al. Kinematics and Trajectory Analysis of the Fixed Abrasive Lapping Process in Machining of Interdigitated Micro-Channels on Bipolar Plates[J]. Precision Engineering, 2016, 44: 192-202.
[23] 肖燏婷, 吴晓峰, 蔡姚杰, 等. 无理偏摆式平面研磨加工均匀性的数值模拟[J]. 机械工程学报, 2021, 57(13): 232-241.
XIAO Yu-ting, WU Xiao-feng, CAI Yao-jie, et al. Numerical Simulation on Uniformity of Plane Lapping with Irrational Swinging Method[J]. Journal of Mechanical Engineering, 2021, 57(13): 232-241.
[24] 刘清, 张广鹏, 高智学, 等.-平面联动的平面研磨轨迹分析与研磨实验[J]. 机械科学与技术, 2018, 37(6): 903-909.
LIU Qing, ZHANG Guang-peng, GAO Zhi-xue, et al. Experimental Study of-Linkage Plane Lapping Track[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(6): 903-909.
[25] FANG Cong-fu, LIU Chong, ZHAO Zai-xing, et al. Study on Geometrical Patterns of Textured Fixed-Abrasive Pads in Sapphire Lapping Based on Trajectory Analysis[J]. Precision Engineering, 2018, 53: 169-178.
[26] 杨晓京, 李明. 平面光学元件研磨抛光磨粒运动轨迹曲率研究[J]. 光学技术, 2017, 43(4): 289-293.
YANG Xiao-jing, LI Ming. Study on the Curvature of the Particle Motion Trajectory in Ultra-Precision Lapping and Polishing[J]. Optical Technique, 2017, 43(4): 289-293.
Modeling Optimization and Uniformity of Cluster Magnetorheological Polishing via Magnetic Trajectory Intensity in Machining Surface
,,
(School of Electromechanical Engineering, Guangdong University of Technology, Guangzhou 510006, China)
Cluster magnetorheological polishing is an efficient planar processing method, which can obtain nano-scale ultra-smooth surface roughness in the polishing process of photovoltaic wafers. The movement mode of the workpiece and the distribution characteristics of the spatial magnetic field have an important effect on the surface uniformity after polishing. The work aims to explore the effects of motion process parameters and spatial magnetic field distribution characteristics on the unevenness of roughness after processing in cluster magnetorheological polishing, and optimize the process parameters to improve the uniformity of surface roughness after processing. A numerical model of the magnetic trajectory intensity including the effective processing trajectory and magnetic trajectory features was proposed. On the basis of the numerical model, the effects of the three motion parameters, namely the rotational speed ratio, the eccentric distance and the reciprocating oscillation, on the two characteristics of the effective processing trajectory and the magnetic trajectory at different positions of the workpiece were analyzed and the speed ratio values in different motion modes were optimized by the model.The polishing experiments of silicon wafers were carried out on a cluster magnetorheological polishing device, and the surface roughness and surface morphology of multiple positions after processing were detected by a white light interferometer, and the roughness distribution was observed. Numerical analysis results showed that the irrational speed ratio could avoid the periodic fluctuation characteristics of different circumferential positions, and choosing the appropriate speed ratio could reduce the difference in the length of the trajectory at different radial positions and improve the uniformity of the trajectory characteristics. Under the condition of irrational speed ratio, changing the eccentricity of the workpiece and increasing the reciprocating swing increased the coverage of the effective processing trajectory, but increased the duty cycle, which resulted in a decrease in the length of the trajectory and a decrease in processing efficiency.Changing the motion pattern of the eccentricity could change the distribution of the magnetic field frequency on the trajectory. Under the condition of the eccentricity 115 mm, the average magnetic field difference between different radial positions of the workpiece was reduced to 0.019 T.The experimental results showed that the variation coefficient of the processed surface roughness under the optimized process parameters was reduced by an average of 37% compared with the control group. The unevenness after polishing in the control group was consistent with the radial distribution law of the magnetic trajectory intensity in the numerical calculation results. At a small speed ratio, the center was smooth and the edge was rough, and at a large speed ratio, the edge was smooth and the center was rough. Under the optimized process conditions of eccentricity of 115 mm and rotational speed ratio of 223∶60, the roughness variation coefficient of the polished silicon wafer was at least 0.309, and the average roughness was4.19 nm.By comparing the experimental results with the numerical simulation results, the numerical model of the magnetictrajectory intensity can effectively optimize the process parameters of the cluster magnetorheological polishing, which is conducive to the matching of the processing trajectory and the magnetic trajectory characteristics, and improves the unevenness of the workpiece after polishing. The method can further provide guidance for the optimal design of the magnetic field generating device and the structure dimension of the motion part of the cluster magnetorheological polishing device.
magnetorheological polishing; numerical analysis; magnetic trajectory; roughness; evenness
TH161
A
1001-3660(2022)12-0243-12
10.16490/j.cnki.issn.1001-3660.2022.12.025
2022–01–11;
2022–04–11
2022-01-11;
2022-04-11
国家自然科学基金(U1801259,52075102)
National Natural Science Foundation of China (U1801259, 52075102)
阎秋生(1962—),男,博士,教授,主要研究方向为光电子/微电子硬脆材料超精密加工理论与技术、材料节能节材加工技术等。
YAN Qiu-sheng (1962-), Male, Doctor, Professor, Research focus: ultra-precision machining of hard and brittle materials.
潘继生(1980—),男,博士,教授,主要研究方向为超精密加工与制造技术、光电晶片平坦化加工工艺、磁流变抛光技术、智能材料开发与应用。
PAN Ji-sheng (1980-), Male, Doctor, Professor, Research focus: flattening processing of optoelectronic wafers.
阎秋生, 梁智镔, 潘继生. 集群磁流变抛光加工表面磁轨迹强度建模优化及加工均匀性研究[J]. 表面技术, 2022, 51(12): 243-254.
YAN Qiu-sheng, LIANG Zhi-bin, PAN Ji-sheng. Modeling Optimization and Uniformity of Cluster Magnetorheological Polishing via Magnetic Trajectory Intensity in Machining Surface[J]. Surface Technology, 2022, 51(12): 243-254.
责任编辑:彭颋
