Adaptive association analysis of rare variants with an ordinal trait based on Cauchy combination test
2023-01-09LINanxingCHENLiliWEIQianran
LI Nanxing, CHEN Lili, WEI Qianran
(School of Mathematical Sciences, Heilongjiang University, Harbin 150080, China)
Abstract: In large-scale biobanks, ordinal traits are common data types, which are used to reflect the human preference, behavior and condition of disease, so, it is valuable to analyze ordinal traits in association analysis.In addition, rare variants can explain additional disease heritability and play an important role in association studies.Therefore, to test association between rare variants and an ordinal trait, a new adaptive association method(CCT-OR)based on Cauchy combination test is proposed, which defines the weighted sum of transformed P values as test statistic.Finally, to further eliminate the noise caused by non-causal variants, an adaptive test statistic is proposed.Simulation studies show that compared to several comparison methods, our proposed method(CCT-OR)is more powerful and robust to the direction of effect of causal variants, and can guard against the effect of non-causal variants.
Keywords: association analysis; rare variant; ordinal trait; ordinal logistic regression
0 Introduction
Large-scale biobanks contain hundreds of thousands of genotyped and extensively phenotyped subjects, which are valuable to identify genetic mechanism[1].In biobanks, there are many ordinal categorical data from surveys and questionnaires[2].These ordinal data reflect human satisfaction, preferences, and behaviors.For such ordinal traits, because there is not any underlying measurable scale, it is not appropriate to take the ordinal trait as a quantitative variable and use the linear regression model.In addition, it is inappropriate to dichotomize the ordinal trait into two categories and use logistic regression model, that would be just emblematic of the power loss.
Both genetic epidemiology studies and electronic health records provide hundreds of thousands of clinically relevant ordinal traits that are associated with the multiple underlying traits[3].Though multivariate association analysis can be carried out based on multiple underlying traits, this method requires more parameters and it is hard to interpret results.However, many association methods pay more attention to dichotomous and/or quantitative traits, seldom to ordinal traits.
With the development of DNA sequencing technology, rare variants(minor allele frequency(MAF)< 5%)can be detected and play an important role in association studies.Due to low MAFs of rare variants, it is not optimal to test a single rare variant by association methods to test a common variant.Hence, a lot of association methods have been proposed to detect the collective effect of multiple rare variants in a gene or region.For rare-variant association studies, burden tests and non-burden tests are the most widely used, such as the sum test(SUM)[4], the weighted sum test(WSS)[5], and the sequence kernel association test(SKAT)[6].However, these methods have advantages and disadvantages, underlying genetic mechanisms are commonly unknown.To further improve power, Seunggeun et al.put forward a data-adaptive optimal test(SKAT-O)[7], which is a linear combination of burden test and SKAT.
To detect rare variants associated with an ordinal trait, we propose a new association method(termed CCT-OR)based on Cauchy combination test[8], which defines the weighted sum of transformedPvalues as test statistic.
1 Materials and methods
Suppose that there arenunrelated individuals, who are sequenced in a gene or region with C rare variants.For theith individual,Yi∈{0,1,…,J}denotes the ordinal trait value,Gic∈{0,1,2}denotes the genotype score at thecth variant site, andXi=(Xi1,Xi2,…,XiL)Tdenotes covariate vector,c=1,2,…,C,i=1,2,…,n.
To enrich association signals of extremely rare variants(a minor-allele count less than a certain number, e.g.,10), the burden method is first used to aggregate extremely rare variants.Then we test the aggregated rare variants and the other rare variants, respectively.Let genotype scores of the aggregated rare variants and the other rare variants beGi0,Gi1,…,GiS.
To test the significance of single variant, we use the ordinal logistic regression model
whereγjis the intercept with ascending level, andγ0≤γ1≤…≤γJ-1;αsrepresents the genetic effect of thesth variant,s=0,1,…,S;β=(β1,β2,…,βL)Tis the regression coefficient vector for covariates.Thus the likelihood ratio test is used to test the null hypothesisH0:αs=0, and the test statistic is given by
Then,p0,p1,…,pSare respectively transformed to Cauchy variables, and weighted combination of these Cauchy variables is taken as the test statistic
(1)
Because there are some non-causal variants in a gene or region, which may cause the noise and affect the performance of association test, we finally use the adaptive association method to exclude the noise caused by non-causal variants.The detailed procedure is as follows.

2)Use the firstk+1smallestpvaluesp′0,p′1,…,p′kto construct statistic
(2)
and obtainS+1 statistics andPvalues, denoted asTCCT-OR-kandpTCCT-OR-k,k=0,1,…,S.
3)The overall statistic is given by
(3)
and obtainPvalue of the statisticTby permutation process.
Because the smallerPvalue is, the more significant an association test is, the idea of statistic(3)is that more significant variants are combined, and the noise caused by non-causal variants is excluded as much as possible.
2 Simulation studies
2.1 Simulation design
Based on the simulation design of Sha et al.[10], we emerge four genes(ADAMTS4, PDE4B, MSH4, and ELAVL4)of GAW17 into a gene with 100 variants.According to the genotype scores of 697 individuals in the gene, we can generate genotype scores ofnsubjects.
To evaluate type Ⅰ error rates, we use the linear regression model
Y=0.5x1+0.5x2+e
(4)
to generate quantitative traits, wherex1andeare two covariates,x1~b(1,0.5), andx2~N(0,1);eis error term, ande~N(0,1).
To evaluate power, the linear regression model
(5)
is used to generate quantitative traits, wherex1,eandeare the same as equation(4);αiandβjare constants and determined by the heritability and minor allele frequencies of rare causal variants, that is
(6)
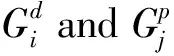
Finally, we use 20%, 40%, 60% and 80% sample percentiles to discretizeYand obtain five categories of ordinal traitYord(= 0,1,2,3,4).In simulation study, we compare CCT-OR with SKAT, SKAT-O, SUM, and WSS.Except for CCT-OR, other methods treat the outcome as dichotomized variable.Specifically, the individual belongs to the control group if the value of ordinal trait is 0; otherwise, the one belongs to the case group.
2.2 Simulation results
To evaluate Type Ⅰ error rates and power,Pvalues are estimated by 1 000 replications, rare variant threshold is set to 0.05, and the sample size is set to 1 000.
For 1 000 replications, the 95% confidence intervals of the estimated type I error rates are(0.003 8, 0.016)and(0.036 2, 0.063 7)at nominal levels 0.01 and 0.05.So, Table 1 shows that all methods can control type I error rates.

Table 1 Type Ⅰ error rates
Table 2 shows that with the increasing of heritability, power of all methods increases, and CCT-OR is more powerful than other methods.The reason for better performance is that CCT-OR uses the ordinal logistic regression model to construct the relationship between an ordinal trait and a rare variant, and makes use of the ordinal feature of traits.Therefore, CCT-OR is an effective method for analyzing ordinal traits.Because only deleterious variants are considered as causal ones in this scenario, WSS is more powerful than SKAT and SKAT-O.From Table 3, we find that CCT-OR is robust to the direction of effect of rare causal variants.In the presence of deleterious and protective variants, SKAT and SKAT-O work better than SUM and WSS.Table 4 presents that power of all methods improves with the increasing of proportion of causal variants.Table 5 shows that by increasing the sample size, the power of all methods can be improved.What’s more, CCT-OR can improve the power rapidly.

Table 2 Power for different heritability

Table 3 Power for different proportions of protective variants

Table 4 Power for different proportions of causal variants

Table 5 Power for different sample sizes
In conclusion, when analyzing ordinal traits, CCT-OR can improve the power of association test and make use of the ordinal feature of traits, compared with methods for dichotomous and/or quantitative traits.
3 Conclusions
In large-scale biobanks, ordinal traits are common data types, which are used to reflect the human behavior and stage of disease.Therefore, it is necessary to develop powerful association methods for analyzing ordinal traits.In this work, we propose an association method(CCT-OR)to detect rare variants associated with an ordinal trait.CCT-OR can guard against the effect of non-causal variants, is robust to the direction of effect of causal variants, and is a powerful association method.So, as an association method for ordinal traits, CCT-OR is valid and feasible.
In view of unknown genetic mechanisms, rare or common variants may be causal in a gene or region, so it is necessary for us to simultaneously detect rare and common causal variants in the future.In addition, ordinal traits are widely observed and sample size distribution for different categories can be unbalanced in biobanks, which can result in inflated type Ⅰ error rates and loss of power.So, we will pay attention to the effect of the unbalanced sample size distribution on association test for analyzing ordinal traits.
Acknowledgments
This research was supported by the Natural Science Foundation of Heilongjiang Province of China(LH2019A020).The Genetic Analysis Workshops are supported by GAW grant R01 GM031575 from the National Institute of General Medical Sciences.Preparation of the Genetic Analysis Workshop 17 Simulated Exome Dataset was supported in part by NIH R01 MH059490 and used sequencing data from the 1 000 Genomes Project(http://www.1000genomes.org).
