基于改进MUSIC 算法的宽带信号DOA 估计

黎昕婷，钟舜聪，钟剑锋

（福州大学机械工程及自动化学院，福州 350108）

0 概述

基于传感器阵列的波达方向（Direction of Arrival，DOA）估计是声纳、雷达、通信、语音处理等领域的研究热点，然而现代化技术发展的需求使DOA 估计不再局限于处理传统窄带信号。在工程实践中，大部分信号是非平稳或谱时变的。在窄带信号源假设条件下，由于源信号的导向矢量具有频率不一致性，因此传统子空间算法，如多重信号分类算法（Multiple Signal Classification，MUSIC）、旋转不变子空间算法（ESPRIT）等，并不适用于工程实践［1-3］。

近年来，研究人员对宽带信号源条件下的DOA估计进行了大量研究［4-6］。宽带信号DOA 估计算法原理上［7］包含非相干信号子空间方法（Incoherent Signals-subspace Method，ISM）［8］与相干信号子空间方 法（Coherent Signals-subspace Method，CSM）［9］。非相干信号子空间方法基于频率分解原理，将宽带源信号分解为一系列窄带信号后进行DOA 估计。相干信号子空间方法基于频率聚焦原理，其中最为典型的是双边相关变换［10］（Two-sided Correlation Transformation，TCT）方法，利用聚焦矩阵将分解得到的子信号变换到参考频率点上，进而使用窄带的处理方法实现DOA 估计。但是该方法需要CSM 预估信号源角度，而聚焦矩阵对预估角度的依赖导致最终DOA 估计结果产生偏差。文献［11］提出一种聚焦的FTOPS 算法，利用参考频点的信号子空间与阵列方向矢量投影矩阵间的正交性对DOA 进行估计。文献［12］对平滑自相关矩阵进行特征分解，再根据特征向量空间之间的过渡性构建聚焦矩阵，从而实现完美聚焦的目的。但是该算法仅针对环境噪声为高斯噪声，并且需要预设参考频率的情况。文献［13］基于压缩感知理论，利用阵列协方差矩阵稀疏迭代估计的方法实现宽带信号DOA 估计，但是该方法在信源数目预估出现错误时，其空间谱结果易产生伪峰。文献［14］对信号子空间聚焦法进行改进，采用奇异值分解重构协方差矩阵，通过Root-正交传播算子实现DOA 估计，改进方法虽然降低了运算量，但是仍需要预估参考频点子频带。文献［15］提出一种频域时延补偿方法，该方法无需对角度进行预估，但是运算复杂度高，难以满足信号实时处理的要求。

针对宽带非平稳信号，研究人员尝试从时频域角度进行研究，根据宽带信号的时频信息获得更准确的DOA 估计结果［16-17］。基于可调窗函数的S 变换和小波变换时频分析方法能进行多分辨率分析。文献［18］构建一种时频域的阵列数据模型，根据信号的时频信息来提高非平稳信号的DOA 估计性能。文献［19］利用小波包变换对信号进行分解，再使用MUSIC 算法对每个子带进行空间谱估计。文献［20］将S 变换应用于MUSIC 算法，并对跳频及交叉chirp 阵列信号进行分析，然而该方法仍存在需要预知信号源个数的问题。文献［21］提出基于小波变换的多重信号分类改进算法，根据信号的时频域特征来提高算法的分辨率。

本文提出一种基于改进MUSIC 算法的宽带信号DOA 估计。通过对接收信号进行S 变换，获得多分辨的时频谱矩阵，同时构建时频域阵列信号模型，根据频率段不同时刻的功率谱矩阵呈联合对角化结构的特点，设计一种新的空间谱，从而实现宽带信号的DOA 估计。

1 基于S 变换的时频阵列数据模型

假设M个阵元等间隔线性排布，阵元间距为d，已知P个宽带信号源sp(t)从不同方向入射，入射角度分别为()θ1，θ2，…，θP，不考虑传播过程中的信号幅值衰减，第m个阵元的接收信号如式（1）所示：

其 中：τmp=(m-1)dsinθp/v为第p个信号到达第m个阵元产生的时延；v为信号的传播速度；nm(t)为第m个阵元的加性噪声。

使用S 变换对信号xm(t)进行处理，变换结果如式（2）所示：

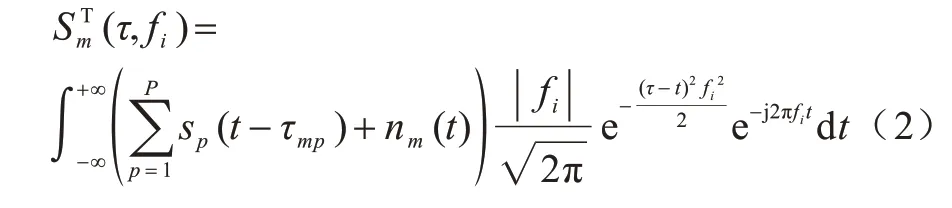
其中：τ为时间因子；fi(i=1，2，…，I)为频率分量。将上式写成傅里叶频谱形式进行推导，如式（3）所示：

其 中：xfi，p(τ-τmp)为信号分量；nfi，m(τ)为噪声分量。假设S 变换的频宽和中心频率满足窄带信号条件，即变换得到的信号分量为窄带信号，如式（4）所示：

在向量形式下，阵列接收信号的时频域模型表示如式（5）所示：

2 ST_MUSIC 算法

2.1 算法原理

根据经典MUSIC 算法原理［22］，ST(τ，fi)的协方差矩阵如式（7）所示：

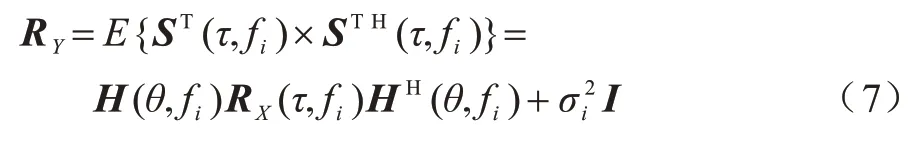
其中：RX(τ，fi)为(τ)的协方差矩阵，由于加性噪声与源信号不相关，且自身互不相关，则变换后的噪声方差可用表示；σi为矩阵奇异值。

由于实际接收数据长度有限，因此数据协方差矩阵取其最大似然估计，如式（8）所示：

对于第n(n=1，2，…，P)个信号源，矢量bn(f)的定义需要满足式（9）：

不考虑噪声项，根据功率谱矩阵的联合对角化结构性质［23］，建立如下等式：

当RY=RY(τk，f)，k=1，2，…，K时，代价函 数［23］的简化结果如式（12）～式（14）所示：

2.2 算法步骤

本文提出的ST_MUSIC 算法主要分为以下5 个步骤：1）根据信号的有效频段设置S 变换的频率分量fi(i=1，2，…，I)；2）利用式（5）对接收信号进行S 变换得ST(τ，fi)，根据式（8）计算得到协方差矩 阵3）根据式（6）构建时频域导向向量h(θ，fi)；4）设置搜索范围和搜索步进Δθ，根据式（15）计算空间谱估计P(θ)；5）通过谱搜索获得P(θ)所有谱峰所在的位置，从而得到DOA 的最大估计值。

2.3 算法分析

根据上述算法原理，ST_MUSIC 算法满足如下条件：

1）本文算法要求符合所有宽带信号的窄带分量互不相关条件；

2）算法可以直接扩展到二维源定位的情况，此时，算法的偏转角表现为方位角与俯仰角的结合，平面范围的谱搜索转变为空间谱搜索，峰值点坐标为DOA 估计结果。

2.4 算法复杂度分析

本文对ST_MUSIC 算法和后续仿真中使用的双边相关变换方法（TCT）、基于压缩感知理论的算法（CS_TCT）［13］及基于小波变换的MUSIC 算 法［21］（CWT_MUSIC）的计算复杂度进行分析。本文设空间谱估计的观测范围的搜索点数为N，信号数据长为L，一个M×M维的数据协方差矩阵做特征分解，其计算量为O(M3)。文献［13］已计算TCT 算法的计算复杂度为O(M3+2N3M3+N2M3)。在k个多频点采用 CS_TCT 算法，其运算复杂度为O(kN3M3+M2)。相 比TCT、CS_TCT 算 法，由 于ST_MUSIC 与CWT_MUSIC 算法中包含的I个尺度参数带来较大的计算量，使算法复杂度显著提升，CWT_MUSIC 算法的总计算量约为O(2IMLlbL+IM3+N)［21］。相 比CWT_MUSIC 算 法，ST_MUSIC算法在谱估计运算中增加了O(IM)的运算量，由于其不需要做特征值分解，总计算量仍小于CWT_MUSIC 算法，为O(2IMLlbL+N+IM)。

3 仿真结果分析

3.1 算法有效性分析

在多声源场景下，本文对ST_MUSIC 算法进行仿真实验，并与TCT、CS_TCT 以及CWT_MUSIC 这3 种算法进行对比。本文采用16 元均匀线性阵列，构建信噪比为0 dB、频率范围为165～300 Hz 的两不相干线性调频信号，设置信号入射角度分别为-20°和20°，采样频率为4 kHz，信号总长度为1 024 个数据点。当阵元数为16 时，CS_TCT、TCT、CWT_MUSIC、ST_MUSIC 算法的空间谱图如图1 所示。从图1 可以看出，4 种算法均可以较准确地估计信号角度，但是估计效果存在差异，当信源数估计不准确时，CS_TCT 算法的伪峰抑制效果受限，而伪峰抑制效果最优的TCT 算法在精度上较其他3 种算法略差，CWT_MUSIC 算法与本文算法具有较优的分辨率和精度。

图1 不同算法的空间谱图对比（阵元数为16）Fig.1 Spatial spectrogram comparison among different algorithms（the number of array elements is 16）

为进一步验证算法的有效性，本文将阵元数减少至12，其他仿真条件不变，进行二次仿真实验。不同算法的空间谱图对比如图2 所示。从图2 可以看出，TCT 算法在阵元数减少后出现多个明显伪峰，结果出现错乱，其他3 种算法对阵元数敏感度低，结果更稳定。CS_TCT 算法估计结果准确度为-20.5°和20.4°。虽然阵元数的减少不影响CS_TCT 算法最终估计结果，但是在算法仿真的零度位置出现较高伪峰。CWT_MUSIC 算法估计结果为-20.8°和20.9°。本文算法估计结果为-20.6°和20.6°，验证了本文算法的有效性。

图2 不同算法的空间谱图对比（阵元数为12）Fig.2 Spatial spectrogram comparison among different algorithms（the number of array elements is 12）

为进一步探究阵元数对算法有效性产生的影响，在同等仿真条件下，ST_MUSIC 算法在不同阵元数下的空间谱图如图3 所示。从图3 可以看出，阵元数的增加使主峰更尖锐，在提高估计精度的同时也会带来更多的旁瓣，但其对估计结果没有影响，而阵元数过少降低估计结果的精度，当阵元数为4 时，DOA 估计结果偏差3°和4°，相比阵元数16，阵元估计结果的误差保持在±0.2°。

图3 在不同阵元数下ST_MUSIC 算法的空间谱图Fig.3 Spatial spectrogram of ST_MUSIC algorithm under different numbers of array elements

3.2 分辨性能对比

本文采用16元均匀线性阵列，信噪比设为-10 dB，分别在信号入射角度相距120°（-45°和75°）、90°（-45°和45°）、60°（-45°和15°）、30°（-20°和10°）、10°（-5°和5°）条件下，进行50 次随机重复实验并计算4 种算法的平均分辨率。分辨率参数采用ρ=[P(θ1)+P(θ2)]/2-min{P(θ1)，P(θ1+Δθ)，…，P(θ2)}［15］，其中θ1、θ2为信号入射角，Δθ为搜索步进，分辨率单位为dB。

在仿真实验中，当信噪比降低为-10 dB 时，TCT算法的仿真结果不稳定，并出现较为严重的伪峰，因此，本节仅对其他3 种算法进行分辨率对比，如表1所示。从表1 可以看出，分辨率随两信号的入射角距增大而增高，基于压缩感知的CS_TCT 算法相较于TCT 算法增大了角度分辨率，且分辨率结果较稳定。本文算法在60°和120°处出现较高的分辨值，但是这3 种算法分辨率差距不大。

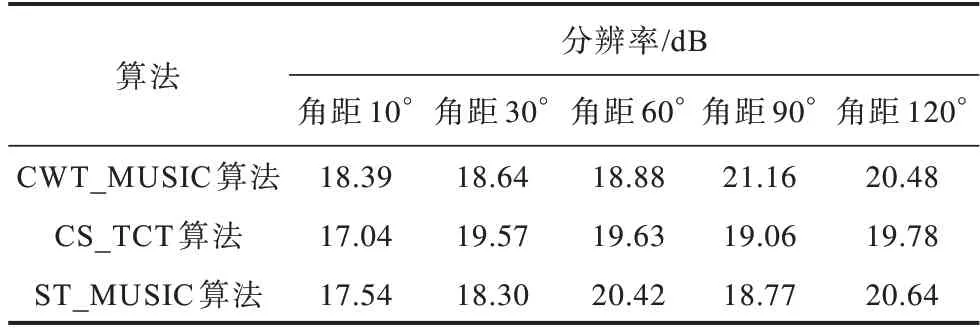
表1 不同算法的分辨率对比Table 1 Resolution comparison among different algorithms

3.3 误差性能对比

本文仿真条件与3.1 节设置一致。本文仿真信号的信噪比范围设置为-15～10 dB，分别通过50 次重复随机实验对比4 种算法DOA 估计结果的均方根误差，如图4 所示。在信噪比为-15 dB 与-10 dB 时，TCT 算法估计的均方根误差大于1°，分别为3.33°、1.60°，因此图4 中未显示其结果，CS_TCT 算法的DOA 估计结果在高信噪比条件下表现更佳。此外，在实验过程中，当信噪比为-15 dB 与-10 dB 时，TCT算法的估计成功率低于50%，而CWT_MUSIC 算法与ST_MUSIC 算法在整个信噪比范围内估计成功率始终保持90%以上。

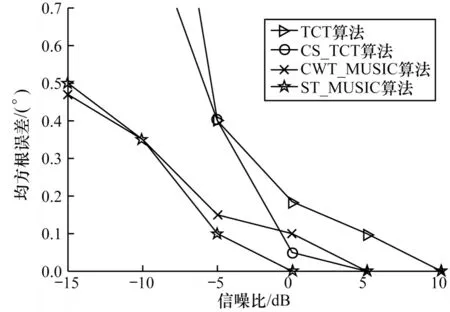
图4 不同算法的均方根误差对比Fig.4 Root mean square error comparison among different algorithms

3.4 计算量对比

本节仿真条件的设置与3.1 节保持一致。本文分别设置2 种仿真情形，分别为2 个信号（-20°和20°）和3 个信号（-60°、-20°和20°），通过50 次随机重复实验对比算法的运算时间。不同算法的平均运算时间如图5 所示，CS_TCT 算法的运算时间最短，与复杂度分析结果对应，基于频率聚焦的TCT 算法明显比基于频率分解的CWT_MUSIC 算法与ST_MUSIC 算法运算时间短，但是这4 种算法的运算时间均在正常可接受范围内，ST_MUSIC 算法略优于CWT_MUSIC 算法。

图5 不同算法的平均运算时间Fig.5 Average computing time of different algorithms

3.5 二维定位仿真实验

本文对所提算法进行二维声源定位仿真实验，其他仿真条件不变，在信噪比为0 dB 条件下，采用真实语音信号进行实验，在不考虑环境混响的情况下，设置2 个语音声源的方位角和俯仰角，分别为40°和40°、40°和-20°，定位结果如图6 所示，从中可以看出，该算法在二维定位中能够得到准确的DOA 估计结果。

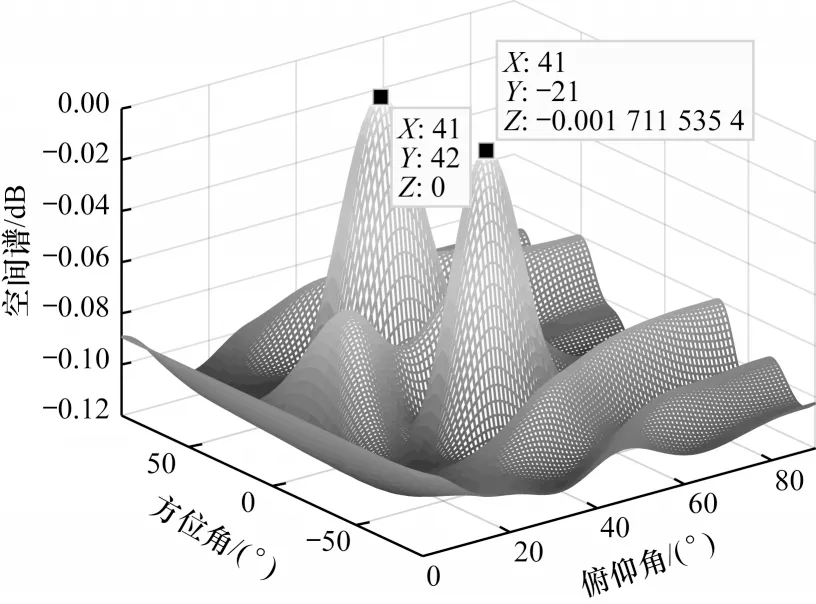
图6 ST_MUSIC 算法的二维DOA 估计谱图Fig.6 Two-dimensional DOA estimation spectrogram of ST_MUSIC algorithm

4 结束语

针对被动探测系统中的宽带信号DOA 估计问题，本文提出一种基于S 变换且无需预估信源数的多重信号分类改进算法。根据S 变换的多分辨率特性，通过构建时频阵列信号模型，提高多源DOA 估计的空间分辨率，利用谱搜索实现DOA 估计，实现多源宽带信号的声源定位。二维语音定位仿真实验验证了该算法的有效性。仿真结果表明，该算法具有较优的分辨率性能和估计性能。后续将从S 变换参数的角度优化本文算法，同时通过增强信号分量、弱化噪声分量，降低算法运算复杂度并提升其在复杂噪声情况下的估计性能。