麻雀搜索算法在路径规划的应用

舒 红

（陕西工业职业技术学院 陕西 咸阳 712000）

0 引言

无论在汽车行业，还是移动机器人行业，路径规划技术都占有核心的地位，且为该行业研究的关键问题。从数学角度出发，路径规划是一个优化问题，但是此问题具有复杂性、约束性等特点。因此，路径规划一直是研究人员的热点问题。

从掌握的环境信息程度不同，可将路径规划分为全局路径规划和局部路径规划。若在已知所有环境信息的情况下完成路径规划，称为全局路径规划。若在只知道局部环境信息或者完全不知道环境信息的情况下完成路径规划，称为局部路径规划。两种路径规划的主要不同点在于：全局路径规划的关键在于规划出全环境的最优路径，而局部路径规划的关键在于利用汽车或者机器人本身的传感器躲避障碍。本文探讨全局路径规划的情况。

在近一个世纪的时间里，国内外研究人员相继提出很多有效路径规划的方法，例如模糊逻辑、人工神经网络、人工势场法等。在设定的环境下，这些方法可以得到较好的效果，但是随着问题越来越复杂，传统方法具有复杂度高、稳定性不好、效率低等缺点，无法满足现阶段对路径规划方面的要求。近些年来，随着人工智能技术的提高，智能优化算法已成为解决路径规划的主要方法，例如蚁群算法、粒子群算法、遗传算法，这些方法都优于传统方法。因为该类算法都可以在规定的具有障碍物空间内搜索最佳路径。

1 蚁群算法

智能优化算法的关键是遗传进化过程，方法是受自然选择和生物进化模型的启发。在路径规划问题中蚁群算法（ACO）应用最为广泛，文献也是最多。MANIEZZO 等[1]学者受在自然界中蚂蚁觅食过程的启发，提出蚂蚁系统，并将其应用到实际寻优路径的环境中得到很好的结果。后来有STUTZLE 等[2]提出了改进的蚁群算法。例如为了防止算法停滞不前，最大最小蚂蚁系统提出了信息素的上下限。BULLNHEIMER[3]提出给不同路径长度设立不同权重的蚂蚁系统，可提高传统蚁群算法的收敛速度。近年来，相关研究人员将传统蚁群算法进行改进并将其应用于不同行业，通过改变自适应变化挥发度的相关参数，来克服蚁群算法易陷入局部最优的问题[4]，以及通过改进启发函数和信息素挥发因子提升蚂蚁搜索的目的性及算法的运算速度[5]。

经过改进之后的蚁群算法解决了路径规划的一些问题，其本身收敛性加快，局部最小问题大幅度减少。但是现实中的路径规划问题有很多类型，且一部分较为复杂。所以，不可能有一种算法可以解决所有类型的问题，也不存在可以解决所有问题的算法。因此，需要不断学习新的算法，且将新算法应用在实际问题中，与已有算法结果进行对比，再进行持续改进。张恩浩[6]在2020年提出麻雀搜索算法（SSA），此算法是受麻雀种群觅食过程和反捕食行为的启发而提出。该算法具有搜索精度高、收敛速度快、高稳定性等明显的优势，很多学者已经对其进行研究并应用在很多行业中。本文将其应用在路径规划的问题中。

2 麻雀搜索算法

麻雀搜索算法的基本思想如下：在算法中，主要有三个类型的个体：发现者、跟随者以及警戒者。发现者是整个种群搜索食物并提供食物方向的个体，而跟随者（加入者）是跟随发现者的方向进行寻找食物的个体，警戒者是负责监视寻找食物的整个区域的个体，一般是处在群体边缘的麻雀，若遇到危险，警戒者则会发布信号，其他个体则会快速向安全地方前进。其中，警戒者一般占种群个数的10%～20%。三种个体通过不断更新自己的位置，最后获得食物[7]。

发现者一般是整个种群中能源储备较高的个体，给加入者提供寻找食物的方向。建立模型的过程中，每个个体的适应度值决定着储备能量的高低。若警戒者意识到危险，则开始发出危险信号。若危险值大于安全值时，发现者将立刻带领加入者到别的安全区域找寻食物。其中发现者和加入者的个体不是固定身份，会动态变化。只要可以找到更好的食物，每个个体都可以转化为发现者身份，但是两类个体在整个种群的比例不会变化。即一个麻雀变为发现者意味着另外一个麻雀成为加入者。且加入者能量储备越低，它们的觅食位置也越差。一些非常饥饿的加入者可能为了获取更多的食物，飞到其他地区寻找食物。

在寻找食物的过程中，加入者不仅可以找到发现者发现最好食物的位置，获得食物，而且能量储备较足的加入者对于发现者也存在危险性，加入者不断监视可找到最好食物的发现者位置，进而抢夺食物资源，提高自身的捕食率。而若遇到危险时，位于群体最外侧的麻雀很快移动到安全地方，处于种群中间位置的麻雀也会随机变动位置。所以种群的每个麻雀位置都会随时变化。本文将每个麻雀的位置用数学符号表示为式（1）。

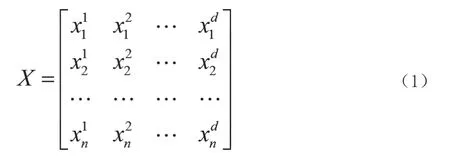
其中，d为未优化问题的变量维度数，n是麻雀的数量。进而所有麻雀的适应度值表示为式（2）。

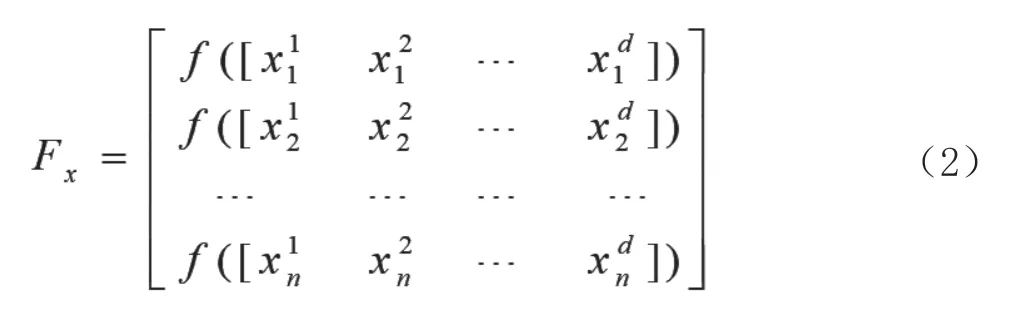
其中，f为适应度值。

在算法中，发现者若有较高的适应度值，则在搜索中会先找到食物。因为发现者需要为整个群体的麻雀觅食，且需要为加入者提供食物的方向。所以，发现者寻找食物的范围比加入者更大。根据式（1）和式（2），发现者在每次迭代的过程中的位置更新表示为式（3）。

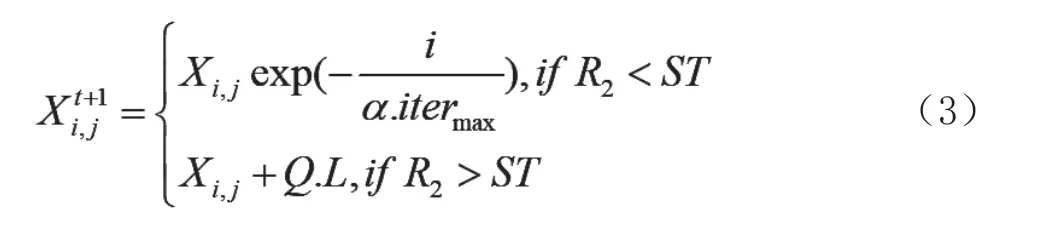
其中，t指当前的迭代数，j=1,2,3…d。itermax指最大迭代次数。指第i个麻雀在第j维的位置信息。a∈[0，1]为随机数。R2∈[0，1]指预警值，ST∈[0.5,1]指安全值。Q为服从正态分布的随机数。L为1×d1×d 的矩阵，该矩阵中每个元素都是1。

式（3）中R2＜ST，指当前的周围环境没有危险，发现者可放心地进行搜索。当R2≥ST时，指群体中的边缘麻雀已经具有危险，并需要向群体的其他麻雀发出警示信号，全部麻雀都需迅速飞到安全区域进行寻找食物。

麻雀群体在寻找食物的过程中，有一些加入者随时盯着发现者。一旦知道发现者找到了更好的食物，就会立刻离开所在位置去争抢食物。如果这些加入者赢了，就可以获得发现者的食物，否则这些加入者继续使用式（4）进行更新位置：

其中，XP指发现者当前占据的最优位置，Xworst指目前全局最差的位置。A为一个1×d的矩阵，将每个元素随机赋值为1 或-1。当i＞n/2 时，说明第i 个加入者处于十分饥饿的状态，适应度值较低，且没有获得食物，需要立即飞向其他地方寻找食物，获得能量。

在仿真实验中，一般假设属于警戒者的麻雀占10%到20%，其初始位置是随机产生的。警戒者的位置更新的数学表达式为式（5）：

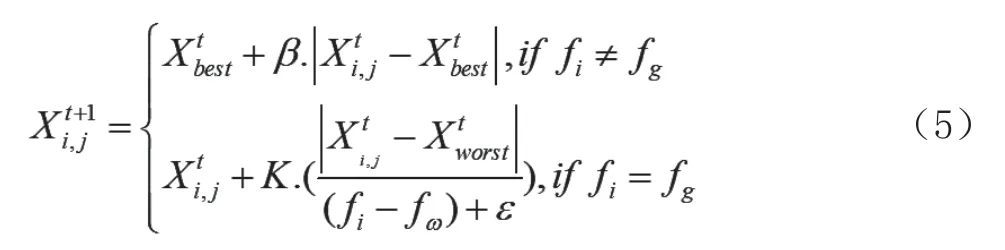
式中，Xbest指目前全局最优位置。β指步长控制参数，一般是服从正态分布的随机数，其均值为0，方差为1。fi指麻雀个体的目前适应度值。fg是当前全局位置最佳适应度值，fw是当前全局位置最差的适应度值。为了避免分母为零，ε为随机一个常数。fi＞fg指麻雀当前正处在群体的边缘，非常容易受到危险者的攻击。Xbest指处在这个位置的麻雀是十分安全的，也是群体中最好的位置。fi=fg指处在群体中间的麻雀感受到了危险，为了减少该类麻雀被害的危险，需要立刻靠近其他麻雀。K∈[-1,1]中的随机数，指步长控制参数[8-10]。

3 算法实现步骤

根据麻雀搜索算法的原理，梳理该算法的流程图见图1。

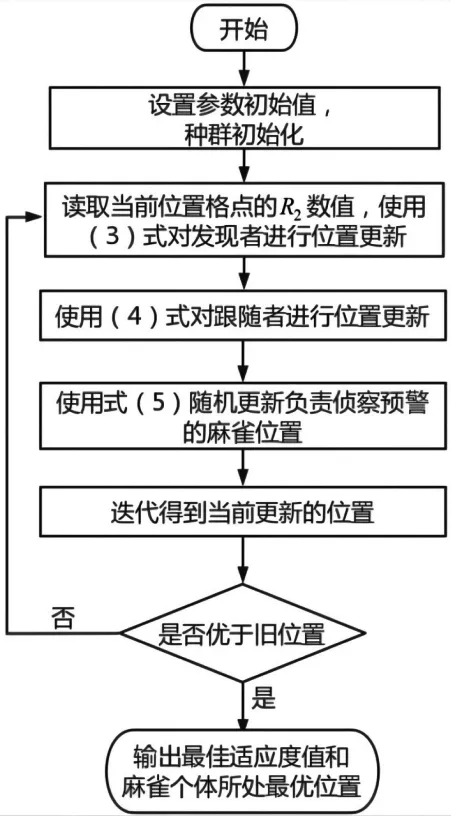
图1 麻雀搜索算法流程图

算法实现步骤主要分为以下9 个步骤：

（1）初始化种群，定义最大迭代次数、种群大小、预警值、安全阈值等基本参数。

（2）设置种群中发现者和加入者的比例，开始进行第一次迭代。

（3）发现者读取当前所在栅格点的R2预警值，使用第（3）式更新发现者的位置。

（4）根据第（4）式更新追随者的位置。

（5）根据式（5）随机更新负责侦察预警的麻雀位置。

（6）迭代结果是当前更新的位置，再判断新位置是否比旧位置更优。

（7）若新位置更优，则替代旧位置。

（8）否则重复进行第（3）步骤到第（7）步骤。

（9）最终输出麻雀个体所处最优位置和最佳适应度数值。

4 仿真实验结果

为了进一步验证麻雀搜索算法的路径规划能力，本文对已知环境使用栅格法建模，使用MATLAB R2018b 仿真软件进行仿真，为了符合更多机器人和更多复杂环境下的路径规划，两种算法都规定种群只在四个方向（上、下、左、右）行走。两种算法的初始种群数量都是20，设置的最大迭代次数都是100。其中麻雀搜索算法的发现者比例为70%，S 为起点，E 为终点。为了验证算法结果不具有偶然性，每个算法在固定参数后都会运行30 次，取平均值。两种算法最终的路径寻优结果及收敛性如图2～图4所示。

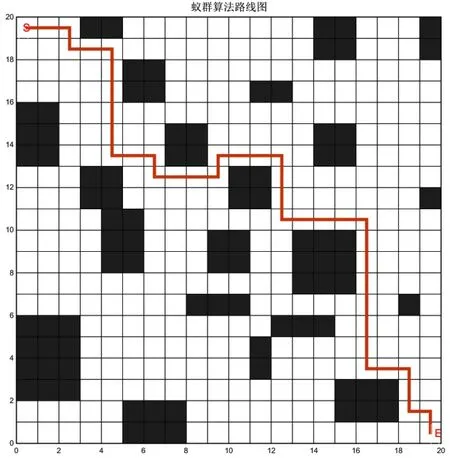
图2 蚁群算法寻优图

图3 麻雀搜索算法寻优图

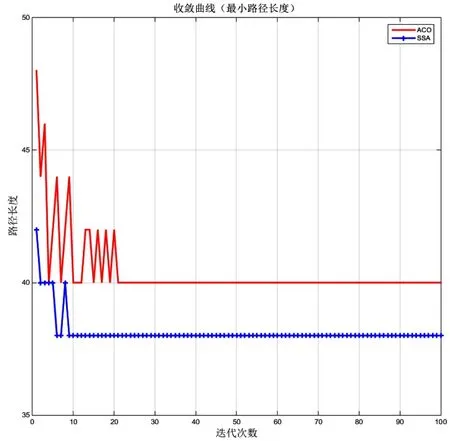
图4 收敛曲线对比图

在30 次的仿真实验后，两种算法在20×20 的栅格地图下的平均最优路径长度、平均最优路径拐点个数以及平均最优路径搜索时间进行汇总对比，见表1所示：

表1 算法寻优结果汇总表

根据以上图表，对仿真结果进行分析，由图2、图3及表1可以明显看出麻雀搜索算法相较于蚁群算法最优路径长度缩短10%，且拐点个数也缩短了35%，完美避开了多障碍物的中心区域，所以麻雀搜索算法的全局搜索能力优于蚁群算法。在最优路径搜索时间方面，麻雀搜索算法运行时间节省约68%。通过图3的收敛曲线对比图，在最大迭代次数相同情况下，麻雀搜索算法在迭代10 次已经趋于稳定，蚁群算法在迭代20 次左右才趋于稳定。通过以上四个角度分析，麻雀搜索算法明显优于蚁群算法的寻优能力，所以麻雀搜索算法更适合在障碍物复杂的环境下找寻最优路径。

5 结论

本文仔细分析了麻雀搜索算法的步骤和算法流程，将算法应用于路径规划问题中，可有效避开复杂障碍物区域，且在路径规划方面有着较好的表现。而且与基本蚁群算法在同一环境下的路径规划结果进行比较，无论是最优路径长短、拐点个数及寻优时间，麻雀搜索算法的结果都明显优于蚁群算法。后续研究将把麻雀搜索算法的局部最优问题进行改进，也将在不同障碍物环境下的搜寻时间进行研究，也尽可能提升此算法的运行速度，节约搜索时间。与此同时，对设置R2预警值与ST安全值与实际环境进行结合，可将此算法应用到更多实际工程优化问题中。