基于组合预测模型的商业银行个人信贷风险预测

戴蓓蓓

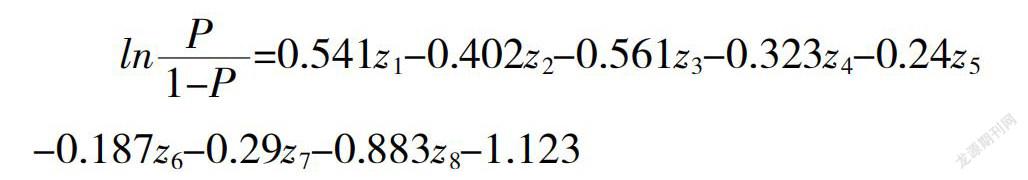
摘   要：商业银行在金融系统中占据举足轻重的位置。提高对个人信贷客户的风险预测能力对降低银行违约坏账、助力金融业健康发展具有积极的现实意义。因此，采用主成分分析法筛选指标，结合多变量判别法和机器学习特点，在误差平方和最小和非负权重约束下，挑选Logistic回归、BP神经网络和决策树构建线性组合预测模型。结果显示，构建的组合模型在个人信用风险预测准确率和第一类误判率表现上优于3种单一模型，并且模型具有较好的泛化稳健性。

关键词：组合预测模型；Logistic回归；BP神经网络；决策树

中图分类号：F832.33      文献标志码：A      文章编号：1673-291X（2022）35-0069-04

商业银行是金融系统的重要组成部分，其信用风险治理能力不仅关系自身运营和大众利益，更影响经济社会健康运转。个人信贷风险是我国商业银行面临的主要风险之一，提升商业银行对个人信贷客户的风险预测能力，是规避银行坏账、避免引发系统性金融风险的重要一环。

个人信用风险预测归根到底是对贷款者按约还款信用“好”和“坏”的分类预测过程。其中预测所选择的方法非常重要。现有研究多采用单一方法对个人信用风险建模分析。根据Bates和Granger提出的组合预测模型的观点，基于多个单项预测方法建立的组合模型会有更高的预测精度。基于此，本文建立一个基于组合预测模型的商业银行个人信用风险预测体系，对商业银行个人客户贷款信用风险量化预测。

一、个人信用评价指标体系构建

本文使用主成分分析法构建个人信用评价指标体系，样本数据来自UCI平台上公开的“German Credit Dataset”真实信息。该数据集共1 000条记录，每条记录中包含20个属性变量和1个类别变量。其中，类别变量是对该条记录的二分类信用评估值。从1 000条记录中随机选择800条数据作为建模样本，200条作为测试样本集1。因样本量有限，另随机选择160条测试样本集2和140条测试样本集3。

主成分分析法是数据降维的常用方法，是将多个相互关联的指标聚合成少数因子，并保留原指标体系绝大部分的信息，达到提高模型处理效能的目的。使用软件SPSS 19.0构建主成分因子。为获得更多的解释信息，挑选前14个方差累计贡献率大于85%的因子作为主成分，通过成分得分系数矩阵，计算出最终的主成分因子得分方程，构建出新的指标体系，如表1所示。

二、单一信用风险预测模型

（一）基于Logistic回歸模型的信用预测

Logistic回归是研究自变量和因变量之间关系的一种非线性回归，它不要求自变量满足正太分布特征，具有较好的判定效果和稳健性。模型中，因变量Y表示个人客户的信用评级。Y=0表示客户具有“好”的信用，贷款违约率低；Y=1表示客户具有“差”的信用，贷款违约率高，银行应拒绝该类客户的贷款申请。对样本建立Y和自变量X的逻辑回归方程：

logit（p）=β0+β1x1+β2x2+β3x3+...+βmxm

在SPSS 19.0中采用后退法（backward conditional）筛选模型自变量，建立Logistic回归模型。每次迭代剔除显著性水平最不明显的变量，直至所有保留变量显著性水平达到建模要求。本文经过7次迭代处理，模型收敛至稳定状态，9个自变量在95%的置信水平下Sig.值均小于0.05，将其引入到Logistic回归模型：

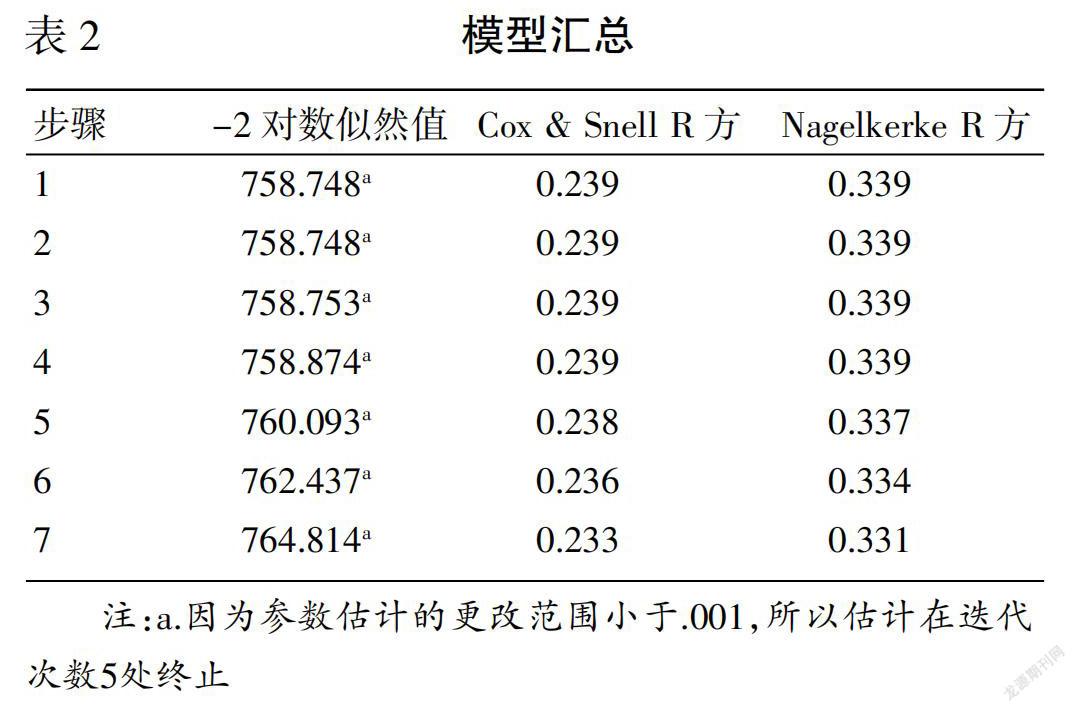
其中，自变量分别代表账户信用影响因子、信用卡状态因子、分期付款占比一般收入、其他分期付款计划、从业年限、性别婚姻状况、是否海外员工、现有账户状态。模型的拟合优度方面，在background conditional的7次运算中，Cox&Snell R方和Nagelkerke R方的值均下降，-2Log likelihood的值不断上升，模型拟合度较好，如表2所示。

使用构建的Logistic 回归模型对建模样本进行预测，发现800条记录中有89条被预测错误，准确率为88.875%。其中，第一类误判率为3.2%，第二类误判率为29.5%。对3组测试样本检验Logistic回归模型的分类预测精度。在最终预测结果中，测试样本1的200条记录中有42条被预测错误，准确率为79%；测试样本2的160条记录中有34条记录被预测错误，准确率为78.75%；测试样本3的140条记录中有22条被预测错误，准确率为84.29%。

（二）基于BP神经网络的信用预测

BP（Back Propagation）神经网络是一种信息正向传播、误差反向修正的多层前馈网络。通过模仿人类大脑神经网络，高效解决数据分类、预测等非线性事务。本文使用MATLB 构建基于BP神经网络的个人信用风险预测模型。模型涉及的数据集是经过主成分分析法处理后的1 000条新数据。使用800条建模样本构建模型，3组测试样本集检验模型的泛化能力。

将原始数据输入到MATLAB阶段需要进行数据的预处理，包括数据编码和归一化处理两步。模型中，BP神经网络的输入数据来自经过主成分分析得到的14个连续数值型的主成分，不需要进行文本数据的编码转换，只需将数据进行归一化处理。

模型结构方面，BP神经网络一般包括1个输入层、1个输出层和1个或多个隐藏层。本文构建3层结构的BP神经网络，输入层的单元数由输入维度决定。每条建模数据具有14个影响模型最终结果的属性变量，即输入层的单元数共有14个。输出层的因变量是1个二分类值，用0表示“好信用”，用1表示“差信用”。此外，隐含层节点数对BP神经网络预测精度有较大的影响。岩节点数太少，神经网络需要增加训练次数，影响预测精度；节点数太多，模型易出现过拟合。本文经过反复试验，确定模型隐藏层单元数为9时具有较好的预测准确率。

将学习率设为0.07、迭代步骤设为700步，为防止数据过度拟合，学习目标即预测值和真实历史值之间的误差平方和设为0.1，开始训练网络。经过700迭代，BP神经网络的误差平方和为0.316。此时模型的预测精度为91.87%，具有较好的训练效果。预测精度方面，800条建模样本中有65条被预测错误，准确率为91.87%。第一类误判率为3.93%；第二类误判率为17.92%。测试样本集中，测试样本1的200条记录中有51条被预测错误，准确率为74.5%；测试样本2的准确率为73.75%；测试样本3的准确率为75.71%。

（三）基于决策树模型的信用预测

决策树由节点和分枝构成，基于样本集推理信息分类规则实现数据预测。对一个数据元组，从根节点自顶向下开始递归，每个内部节点基于某种属性信息完成判断，构成决策树从根节点到叶子节点的分类规则。使用C5.0算法在SPSS Clementine 12.0中构建决策树。输入变量是14个相互独立的主成分因子，输出变量是对客户的信用评级。

决策树是一种“有导师”的学习机制，通过对样本的反复训练，建立分类推理规则，并将其应用在新样本分类预测中。为提高模型对样本的拟合度和预测精度，在C5.0算法中应用Boosting技术。经过6次迭代，共建立6个具有不同预测精度的相关模型。为规避样本过度

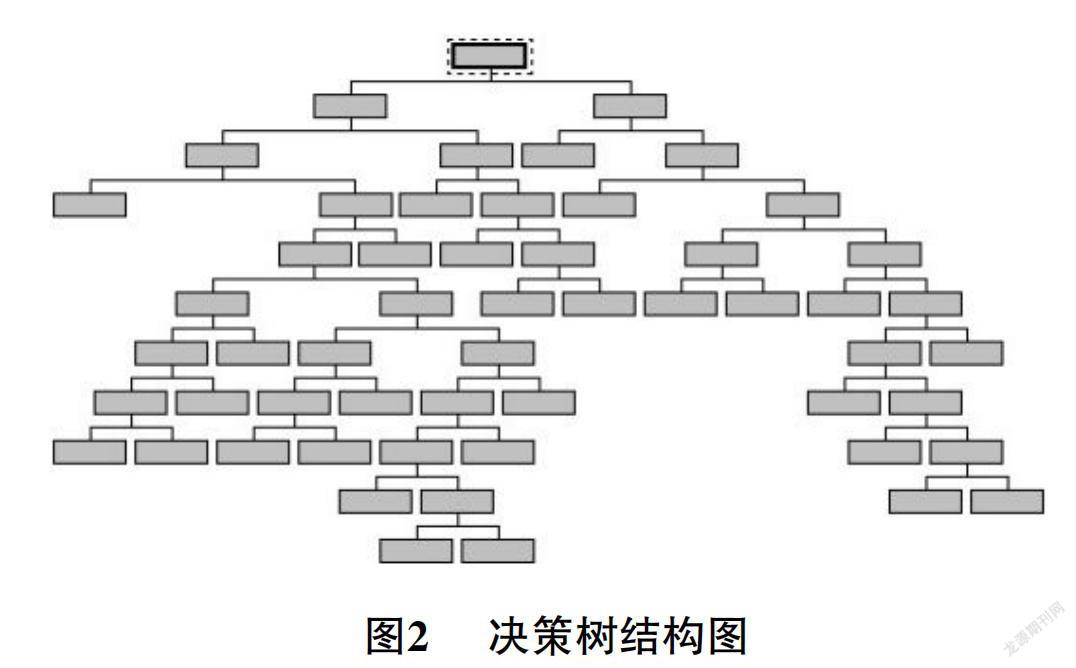
拟合，C5.0算法对决策树采取“后剪枝”处理，本文设定75%的剪枝率，即保留25%的原始决策树信息。得到的决策树分类规则和树状结构图如图2。

在检验样本集中，样本的置信度区间为0.5—1，即样本的预测置信度最小值为0.5，最大值为1。对于正确预测的样本，预测置信度的平均值为0.837，对于错误预测的样本，其预测置信度的平均值为0.625。预测置信度在0.876以上的样本中有38%通常是正确的，预测置信度在0.511以上的样本中有90.12%通常是正确的。

决策树模型基于建模样本集的预测精度为89%，说明800条样本中712条预测正确，88条预测错误。其中，第一类误判率为2.32%，第二类误判率为31.25%。对测试样本集中的3组测试样本检验决策树模型的分类预测精度。在最终预测结果中，测试样本1的准确率为76.5%，测试样本2的准确率为77.5%，测试样本3的准确率为77.86%。

三、个人信用评估组合预测模型

单一预测模型一般过滤掉对结果影响不显著的因子和信息，在数据去噪的同时造成不同程度的信息丢失；且各单一模型的理论逻辑存在差异，过滤的信息维度不同，影响综合维度表征下结果的预测精度。组合预测模型，通过线性或非线性方式聚合单一预测方法，最大化综合各单一模型涵盖的信息，提高预测精度和有效性。本文使用线性方式组合单一预测模型，记组合预测模型的预测值误差平方和为：

基于误差平方和最小的组合预测模型可表示为：

构建拉格朗日函数，极小值存在条件下一阶导为0，MATLAB下使用最小二乘法，求得组合预测模型中各单一模型所占权重：

w1=0.280 3，w2=0.429 5，w3=0.290 2

据此，可构建商业银行个人信用风险预测组合预测模型：

y=0.280 3y1+0.429 5y2+0.290 2y3

四、模型对比分析

比较Logistic回归、BP神經网络、决策树3个单一模型和组合预测模型的分类预测精度和稳定性。

（一）分类预测精度比较

在建模预测分类精度方面，组合预测模型分类精度为92.5%，高于3个单一模型的分类预测准确率。单一模型中，BP神经网络具有最好的数据拟合度，Logistic回归模型预测分类精度低于BP神经网络和决策树模型，决策树模型介于二者中间，分类精度为89%。误判率方面，第二类误判率最低的是BP神经网络模型，组合预测模型的误判率低于决策树和Logistic回归模型，高于BP神经网络。第一类误判率最低的是组合预测模型，为0.36%，它对建模预测样本中所有的“好信用”记录都能较准确地进行分类。

测试样本上，组合预测模型在3组测试样本上的预测精度均值为82.828%，优于单一模型的均值表现；组合预测模型在测试样本1和2上的分类预测准确率高于单一模型，在测试样本3上的分类预测准确率高于BP神经网络和决策树模型，低于Logistic回归模型。说明组合预测模型的预测精度不一定高于单一模型，和测试样本集的选取有很大关系。在误判率的均值表现上，组合预测模型低于单一模型，说明组合预测模型比单一模型具有更好的纠错能力。

（二）模型稳健性比较

稳健性衡量模型的泛化能力。评估当样本数据发生改变时，模型能否正常工作，是否仍能保持较高水平的精度和有效性。统计学上，一般采用标准差衡量模型针对不同样本时的波动性，波动性越小，样本的泛化推广能力越好。在总分类预测精度标准差和第一类误判率标准差上，组合预测模型的值分别为0.002 6和0.005 7，低于3个单一模型，对检验样本的分类预测精度的波动较小；在第二类误判率标准差上，组合预测模型值为0.036 7，高于3个单一模型。总体上，模型的稳健性较单一模型表现好，即训练后的模型对新样本的适应性较好。

五、结论

本文借鉴国内外信用风险预测相关研究，探讨组合预测模型在风险客户分类预测方面的应用。在采用主成分分析法重建信用评估指标的基础上，构建基于Logistic 回归、BP 神经网络和决策树的组合预测模型。三种单一模型分属多变量判别法和机器学习两类方法，运作机理不同，具有一定的信息维度互补作用。且BP 神经网络较Logistic 回归模型具有更好的数据拟合能力，但新样本集上模型预测能力较差。为提升精度，同时平衡组合模型的稳健性，组合模型引入决策树。通过实证对比分析说明，构建的组合模型在个人信用风险预测准确率和第一类误判率表现上优于3种单一模型，并且模型具有较好的泛化稳健性。但本文仅将预测结果做二分类处理，在今后的工作中，将细化客户信用评估级别，对不同的客户信用等级采取不同授信处理。

参考文献：

[1]   方先明，熊鹏.对商业银行信用风险监测评价的新思考[J].中央财经大学学报，2005，（7）：13-18.

[2]   张晨，万相昱.大数据背景下个人信用评估体系建设和评估模型构建[J].征信，2019，37（10）：66-71.

[3]   王丰效.最小机会损失的组合预测模型精度评价[J].统计与决策，2013，（21）：37-39.

[4]   黄亚驹，等.基于混合算法和BP神经网络的网络舆情预测研究[J].情报科学，2018，36（2）：24-29.

[5]   孙铁柱，等.基于CRT分类算法的用户画像分层模型—以银行借贷用户为例[J].情报科学，2020，38（9）：75-81.

[6]   杨胜刚，等.个人信用评估组合模型的构建——基于决策树-神经网络的研究[J].金融论坛，2013，18（2）：57-61，67.

[7]   杨剑锋，等.机器学习分类问题及算法研究综述[J].统计与决策，2019，（6）：36-40.

[8]   邱晗，黄益平，纪洋，等.金融科技对传统银行行为的影响——基于互联网理财的视角[J].金融研究，2018，（11）：17-29.

[责任编辑   妤   文]