罗茨真空泵偏心大圆弧转子型线设计及分析
2023-01-06李正清李小金杨建斌刘筱文韩仙虎蔡宇宏李晓霞
李正清,李小金,杨建斌,刘筱文,韩仙虎,蔡宇宏,王 毅,李晓霞
(兰州空间技术物理研究所,兰州 730000)
0 引言
罗茨泵具有启动快、功耗小、抽速大、效率高、维护费用低等特点,被广泛应用于半导体、冶金、化工、医药等行业中。罗茨泵是一种双转子回转式容积真空泵。工作过程中罗茨泵的一对转子相向转动,将气体由进口端输运至出口端实现抽气,转子在运转过程中相互啮合,以减少气体逆向流动形成的返流。罗茨泵转子型线的啮合设计非常重要,直接关系到真空泵的各项性能指标[1-2]。
常见的转子型线主要分为3类:摆线型、渐开线型和圆弧型[3-11]。在不同的顶圆半径和节圆半径下设计及分析常见转子型线,应用于罗茨泵产品的设计是型线研究的重要内容[3-5]。张帅等[6]应用该方法分析罗茨泵转子外摆线和内摆线,设计了双叶型罗茨泵摆线转子型线;戴映红等[7]采用此方法设计了气冷罗茨真空泵转子的摆线-圆弧型线。上述转子型线的设计均采用几何分析的方法,该方法虽然易于理解,但求解过程复杂,计算分析量大。探索新的转子型线,设计分析新型线的特性是转子型线研究的重要内容之一。标准圆弧型转子型线中,圆弧中心均位于转子型线的对称轴上,形成由圆弧及其共轭曲线共同组成的转子型线[8]。偏心圆弧转子型线由中心位于节圆内的圆弧及顶部密封圆弧构成,能有效提高转子的容积利用率,但在偏心圆弧和顶部密封圆弧间必须采用过渡曲线,使得转子部分位置的间隙偏大[9]。在偏心大圆弧转子型线中,圆弧中心位于节圆内腰部曲线对应的轴上,圆弧半径远大于传统圆弧转子型线半径。本文首先确定转子的偏心大圆弧及对应销齿圆弧,然后应用转子啮合特性,基于偏心大圆弧参数获得其对应的共轭曲线,形成由偏心大圆弧、销齿圆弧及偏心大圆弧共轭曲线构成的光滑连接的转子型线,使得设计及计算过程简化;其次,应用共轭特性,构建基于理论型线的实际型线设计方法,实现转子均匀间隙的设计。最后,以70 L/s抽速的罗茨泵为目标,完成转子型线设计及分析。
1 转子型线分析
如图1所示,罗茨泵转子型线为中心和轴对称曲线,因此仅须求解整个转子型线的1/4即可。偏心大圆弧转子型线中,节圆半径为R1;AE为偏心大圆弧,圆心O1位于x1轴负半轴,半径为R2,F为偏心大圆弧上任一点,半径O1F与节圆相交于D,根据啮合特性,φ角为F点的啮合角;CE为顶部销齿圆弧,圆心位于节圆上P点,半径为R3;腰部曲线AG为偏心大圆弧AE对应的共轭曲线,BG为腰部销齿圆弧,圆心位于节圆上H点,半径为R3;转子的顶圆半径为R4。

图1 罗茨泵偏心大圆弧转子型线Fig.1 Eccentric large arc rotor profile of Roots vacuum pump
1.1 节圆外型线分析
偏心大圆弧转子型线分析如图2所示,连接O1A,在ΔKAH中,AH的长度可表示为:

图2 偏心大圆弧转子型线分析Fig.2 Eccentric large arc rotor profile analyzes

假设O1K的长度为l,则O1H的长度为2R1-l。
在ΔO1AH中,偏心大圆弧AE对应的半径R2由余弦定理可表示为:

圆弧AE的方程可以表示为:

圆弧AE方程中变量α在ΔO1AH中取得最小值,由余弦定理可表示为:

在ΔO1PO中,O1P的长度可以表示为:
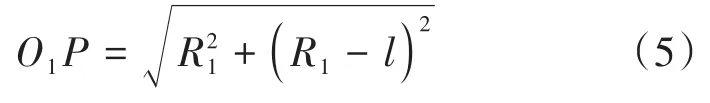

顶部圆弧CE是以P点为圆心,以PE为半径的销齿圆弧,因此,销齿圆弧CE的方程可以表示为:

销齿圆弧的半径R3=R2-O1P。由图2可知,方程(7)中自变量γ的最小值为零,在ΔO1PO中可以确定γ的最大值为:

此时转子顶圆半径R4=R1+R3。
应用啮合特性求解转子共轭曲线对应的型线时,须求解转子的啮合角φ,啮合角为啮合点法线O1F与节圆的交点D和转子中心的连线与坐标轴y1的夹角。
在ΔO1DO中,应用正弦定理,β可以表示为:

啮合角φ可以表示为:

1.2 共轭曲线部分
根据罗茨泵转子的啮合特性,共轭曲线的坐标转换关系可表示为[12]:
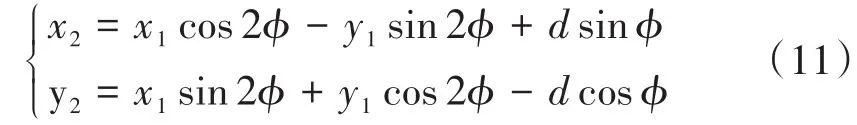
式中:d为两坐标系原点间的距离即为2个转子中心的距离,由式(11)可确定转子偏心大圆弧AE对应的共轭曲线部分,其中变量φ值由式(10)确定,(x1,y1)值由偏心大圆弧线式(3)确定。如图1所示,共轭方程式(11)确定的共轭曲线位于x2O2y2坐标系中(位于转子2中),需将其平移至转子1中,并逆时针旋转π/2。顶部销齿圆弧与腰部销齿圆弧BG互为共轭曲线,其方程可以表示为:

自变量γ的取值范围为(0,π/2-αmax)。
综上,根据式(3)(7)(11)和(12)便可获得整个转子型线的1/4,然后由转子的轴对称性,获得整个转子的型线。
1.3 转子实际型线
转子理论型线的设计间隙为零,转子在每个啮合点接触。在实际的转子型线设计中,由于加工误差、应力变形以及热变形的存在,必须设计适当的间隙,确保转子的正常运行。因此,分析求解转子的实际型线是转子型线设计的重要组成部分[13]。
实际型线求解可分为几何法和解析法。采用几何法,须具体分析建立每种实际型线与理论型线的参数关系;采用解析法仅须对型线方程进行求导计算便可获得实际型线,该方法适用性广,各种型线的求解步骤相同。基于此,采用解析法分析设计偏心大圆弧转子实际型线。
如图3所示,位于节圆外的任一转子型线AC的参数方程可表示为:

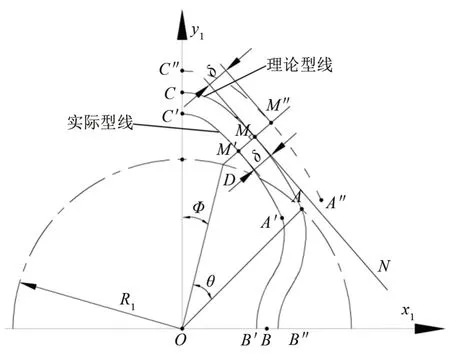
图3 转子理论和实际型线Fig.3 Theoretical and actual profile
设M为型线AC上任一点,过该点转子型线的切线为MN,过M点做切线的垂线,垂线交节圆于D点,设罗茨泵转子间隙为2δ,则对于单个转子实际型线需要在法线方向缩进δ,如图3中,理论型线上M点对应的实际转子型线点为M'。
设M点的坐标为(x1,y1),则过M点转子理论型线的切线MN的斜率kMN可表示为:

法线MD与切线MN垂直,因此法线斜率与切线斜率的乘积为-1,则法线MD的斜率kMD可表示为:
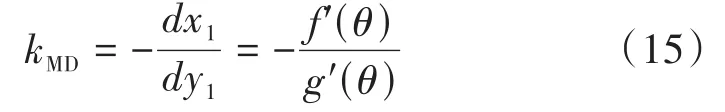
过M点,法线MD方向的单位向量可以表示为:

由于理论型线和实际型线间的距离为δ,因此根据式(14)~(16),图3中已知理论型线AC对应的实际型线A'C'可以表示为:

基于式(15)~(17),采用解析法可获得转子的实际型线。若共轭曲线也采用这种方法,须将已知型线式(13)和啮合角式(10)代入式(11),然后由式(15)~(17)获得实际型线。显然,将式(13)和(10)代入(11)形成的表达式很复杂,不利于实际型线的求解。为了简化求解过程,根据转子共轭啮合特性,可首先将已知曲线AC沿法线向外延长δ,然后求解该段曲线对应的共轭曲线即得到腰部实际型线的对应部分。
如图3所示,将转子理论型线AC部分向外延伸δ得到的曲线A''C''可表示为:

将由式(18)确定的曲线A''C''的参数代入共轭方程式(11),便可获得对应转子2的共轭曲线。根据啮合特性,转子1的型线向外延长,必然导致转子2型线向内收缩δ以保持两者间的啮合关系。然后将其通过平移和旋转移动至转子1中便可获得理论型线AB部分的实际型线A'B'。
综上,已知型线方程求解实际型线可分为2步:(1)根据式(16)求解型线法向单位向量;(2)根据式(17)求解实际型线。已知型线方程求解其共轭曲线对应的实际型线可分为3步:(1)根据式(16)求解单位向量;(2)根据式(18)求解向外偏置型线;(3)将由式(18)计算得到的参数代入共轭方程式(11)获得实际型线。
2 转子型线设计
2.1 转子理论型线
按照上述分析步骤,设计罗茨泵产品实际抽速为70 L/s,转速3 000 r/min,有效抽速为几何抽速的75%,转子节圆半径为R1=34 mm,顶圆半径R4取48~48.5 mm,由式(1)(2)和(5)可得R4与l的关系,如式(19)所示。在转子间隙δ=0.1 mm的条件下,分析计算转子偏心大圆弧圆心位置l、半径R2,顶部销齿圆弧半径R3和转子长度lrotor。

转子1/4部分型线的偏心大圆弧AE由式(3)确定,顶部圆弧CE段由式(7)确定,AE对应的共轭曲线部分AG由共轭方程式(11)确定,腰部销齿圆弧由式(12)确定。当顶圆半径R4取不同值时,首先获得转子1/4型线,然后以坐标轴为对称轴将1/4转子型线取对称,即获得整个转子理论型线。最后,由1.3节中依据理论型线求解实际型线的方法获得转子实际型线。如图4所示(图中为了显示清晰,间隙取值为2 mm)。偏心大圆弧圆心位置l,偏心大圆弧半径R2、销齿圆弧半径R3及转子长度lrotor如表1所列。

图4 偏心大圆弧转子理论及实际型线Fig.4 Theoretical and actual profile of eccentric large arc rotor
由表1可知,当节圆半径R1给定时,随着顶圆半径R4减小,偏心大圆弧圆心与节圆的距离l增加,半径R2减小,销齿圆弧半径R3减小。由于整机设计抽速不变,随着转子顶圆半径R4减小,转子腔室截面积减小,为保持整机抽速恒定,须增加转子长度lrotor,因此转子长度lrotor随转子顶圆半径R4减小而增大。
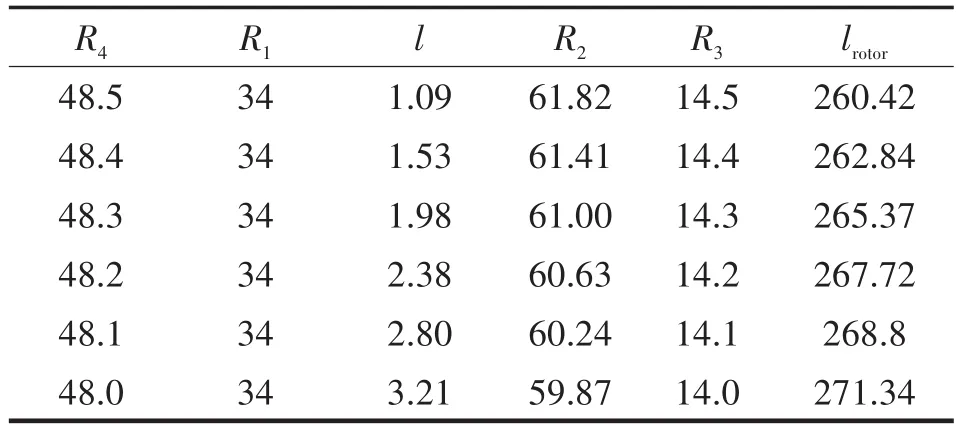
表1 不同的R4值下转子设计参数Tab.1 Design parameters of profile at differentR4单位:mm
2.2 容积利用系数
罗茨泵转子容积利用系数为转子顶圆面积与截面面积的差值与转子顶圆面积的比值,表征罗茨泵转子的空间利用程度。

式中:C为罗茨泵转子容积利用系数;B为罗茨泵转子截面积。
转子参数对应的容积利用系数如图5所示。可以看到,在相同的顶圆半径下,偏心大圆弧转子型线的容积利用系数优于标准圆弧型线的容积利用系数。

图5 转子型线的容积利用系数Fig.5 Volume utilization of profile
2.3 转子型线讨论
从表1可以看出,转子型线上偏心大圆弧的圆心均位于节圆内部。若在节圆半径不变的条件下增加顶圆半径,则偏心大圆弧的圆心将位于节圆外部x1轴上。此时形成的转子型线将出现圆弧线及其共轭曲线的切线斜率不相等的情形,共轭曲线部分变成折线,如图6所示。

图6 罗茨泵转子型线变成折线Fig.6 Rotor profile form undercutting
因此在设计偏心大圆弧转子型线时,偏心大圆弧的圆心不能位于x1轴节圆外。
3 结论
通过将罗茨泵转子型线的圆弧中心设计在腰部曲线对应轴上,进行了偏心大圆弧转子型线设计;同时,基于共轭特性分析了理论型线和实际型线的转化关系,并以实际抽速为70 L/s的罗茨泵为设计目标,完成了罗茨泵偏心大圆弧转子型线的设计及分析,得到以下结论:
(1)偏心大圆弧转子型线由偏心大圆弧、销齿圆弧及偏心大圆弧对应的共轭曲线三部分构成。
(2)构建了基于转子理论型线的实际型线设计方法,特别是在分析共轭曲线的实际型线时,采用将已知型线向外延伸,然后求解获得共轭曲线的实际型线方法,使得求解过程大幅简化。
(3)以实际抽速为70 L/s的罗茨泵为设计目标,分析计算了在节圆半径不变情形下,型线顶圆半径、销齿圆弧半径、转子长度及容积利用系数等参数。
