MC-Q强化学习的PHEV能量管理策略
2023-01-06王惠庆
王惠庆
MC-Q强化学习的PHEV能量管理策略
王惠庆
(长安大学 汽车学院,陕西 西安 710064)
插电式混合动力汽车具有节能的特点,而多动力源之间的能量管理策略对混合动力汽车能耗有很大的影响,故文章以一款在固定线路上运行的串联插电式混合动力城市客车为例,基于以往的行驶工况,根据马尔科夫理论,把需求功率随时间的变化转换为状态转移矩阵,用概率矩阵生成符合实际使用条件的随机功率序列。建立Q强化学习模块,使用得到的随机功率序列进行训练,实现城市客车能量分配的实时优化控制。仿真结果表明,文章所提出的强化学习能量管理算法相比于规则控制算法能明显的优化能耗,对比动态规划全局优化策略总能耗仅轻微增长,控制策略可实现实时应用。
插电式混合动力汽车;能量管理;强化学习;转移概率矩阵
能量管理策略对插电式混合动力汽车(Plug- in hybrid electric vehicle, PHEV)的能耗效率有很大的影响,各国研究人员已经提出了很多的能量管理策略,包括基于规则的消耗-维持(Charge Depletion-Charge Sustaining, CD-CS)策略,基于全局优化的动态规划和庞特里亚金最大化原理(Pontryagin's Maximum Principle, PMP)控制策略,和可实时应用的等效燃油最小化策略等。近年来,针对强化学习的研究越来越多[1],而Q学习算法作为一种用于机器学习,基于数据的与模型无关的强化学习算法,被越来越多用于混合动力汽车的能量管理策略当中[2]。但针对插电式混合动力汽车强化Q学习算法的能量管理策略研究较少,而且强化学习要求的样本量较大,使用实际工况很难训练出较好结果。
针对以上问题,本文基于一款固定路线运行的插电式混合动力城市客车,在传统的Q学习算法的基础上,用实测西安工况得到关于功率的马尔科夫状态转移矩阵,生成随机功率序列训练Q学习矩阵,得到MC-Q能量管理算法。最终实现针对插电式混合动力汽车能量管理的实时控制,并把仿真结果与动态规划(Dynamic Programming, DP)算法和CD-CS算法相比较。
1 整车建模及仿真工况
1.1 整车参数
本文所选取的PHEV动力系统结构如图1所示,发动机和集成式智能启动驱动(Integrated Starter Generator, ISG)电机共同组成发动机驱动型发电机(Engine Generator Unit, EGU)单元,与驱动电机串联,把发动机提供的机械能转换为电能,驱动车辆行驶,车辆可以通过外接电源为磷酸铁锂电池充电,该款车型整备质量为13 500 kg,轮边减速器减速比为13.9,采用双电机驱动,单体电池电压为3.2 V,电池总电压为537.6 V,总容量为180 Ah。
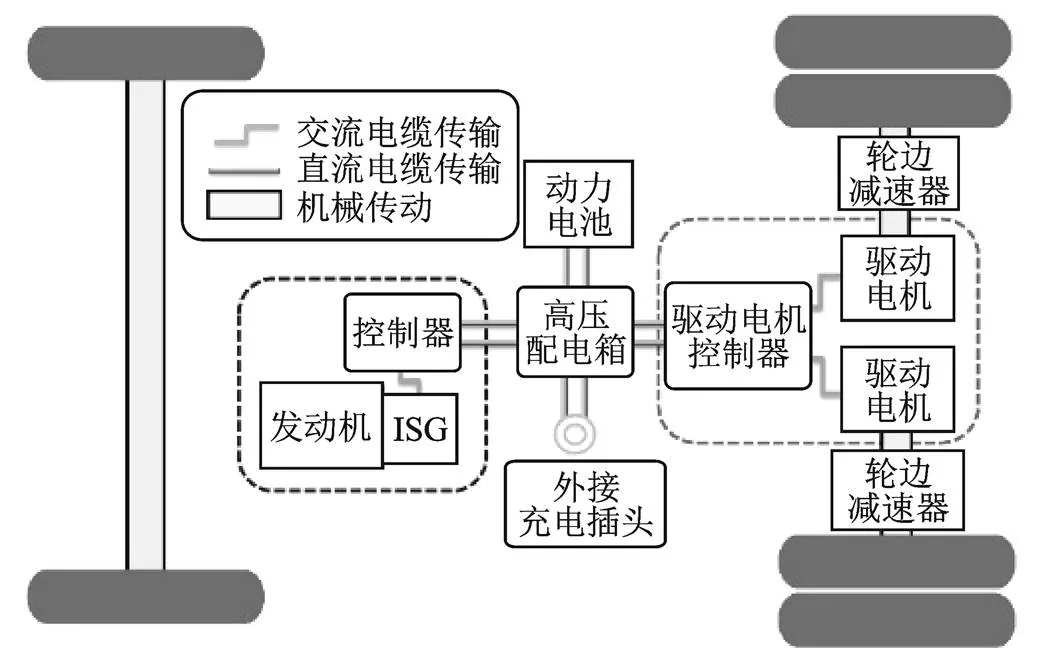
图1 PHEV动力系统结构
1.2 车辆纵向动力学模型
根据汽车理论汽车行驶平衡方程[5],车辆纵向动力学模型可以表示为
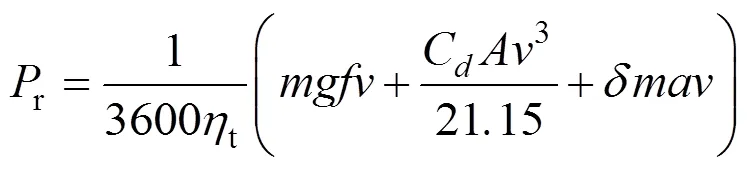
式中,为总质量;为重力加速度;为滚动阻力系数;为车速;d为空气阻力系数;为车辆迎风面积;为汽车旋转质量换算系数;为加速度;t为传动系统机械效率;r为车辆行驶的需求功率。
车辆需求功率和电池输出功率b和EGU输出功率的egu关系为
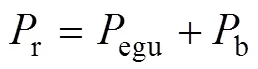
1.3 动力部件模型
对于发动机和驱动电机,根据稳态实验建模数据,可以把它们的效率或者油耗表示为随转矩和转速改变的函数,它们的效率如图2和图3所示。
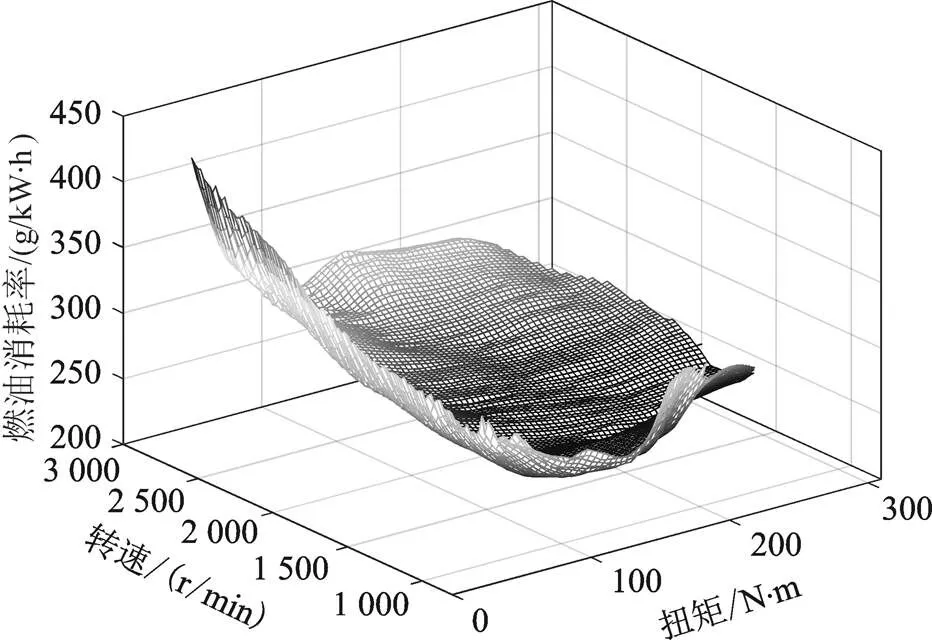
图2 发动机万有特性图
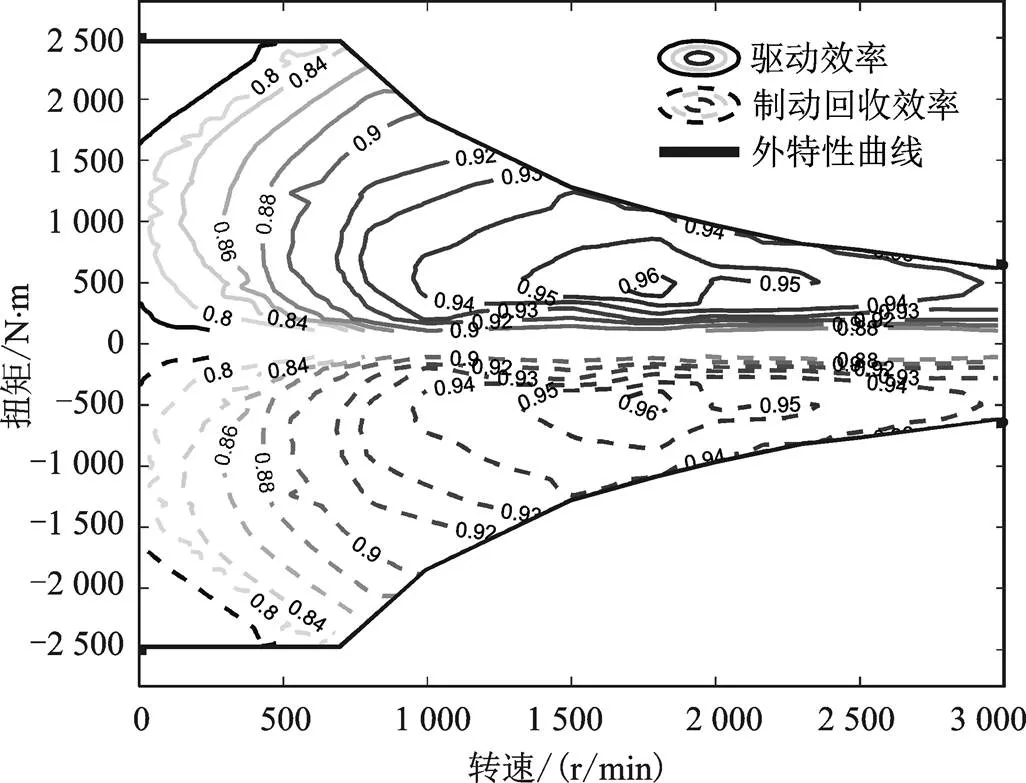
图3 电机效率图
1.4 仿真工况
本文依据实测得到的西安市城市工况,选择了同一公交路线下同一时段不同日期测得的两条速度谱,分别作为训练工况和测试工况,两个工况的总长度都是140.15 km,速度谱如图4所示。
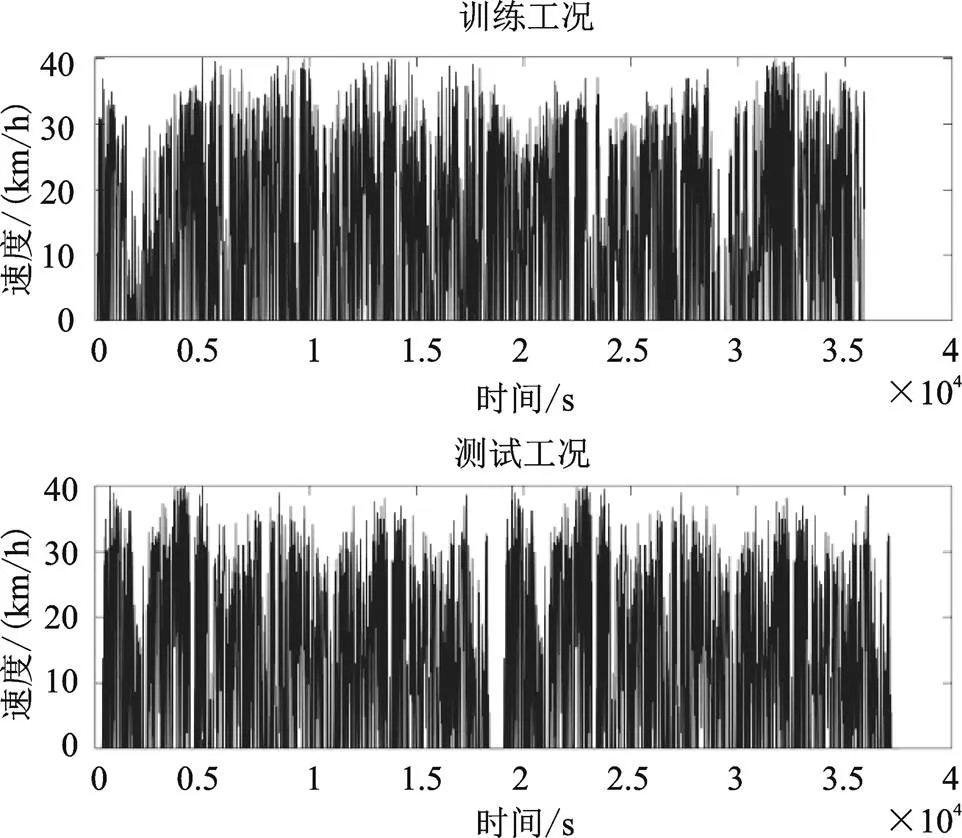
图4 仿真工况
2 MC-Q学习算法能量管理策略构建
相比于传统的基于Q学习算法能量管理策略,本文所提出的MC-Q学习能量管理控制算法,创新点在于训练工况不是直接使用实测工况,而是把实测工况根据马尔科夫理论转换为概率转移矩阵,依据得到的概率矩阵生成随机工况序列,这样可以在每一个训练循环当中,使用符合目标车辆实际使用情况,但又完全不同的需求功率序列进行训练,大大丰富了样本的复杂程度,防止训练结果过早的陷入局部收敛当中。
2.1 需求功率转移概率矩阵
根据选择的测试工况,基于车辆的动力学方程(1),可以计算出需求功率,而需求功率可以看成是一个马尔科夫过程[1],后一时刻的功率只与当前时刻有关,与以往无关。对需求功率进行离散化,用最大似然法和最邻近法求转移概率[2]
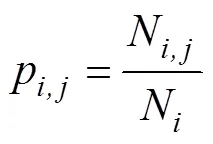
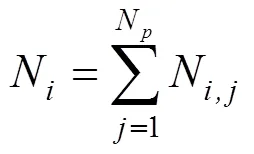
式中,N表示离散的需求功率从P转移到P的次数;而N表示需求功率P出现的总次数;N为下一时刻状态数量;得到的状态转移概率矩阵如图5所示。
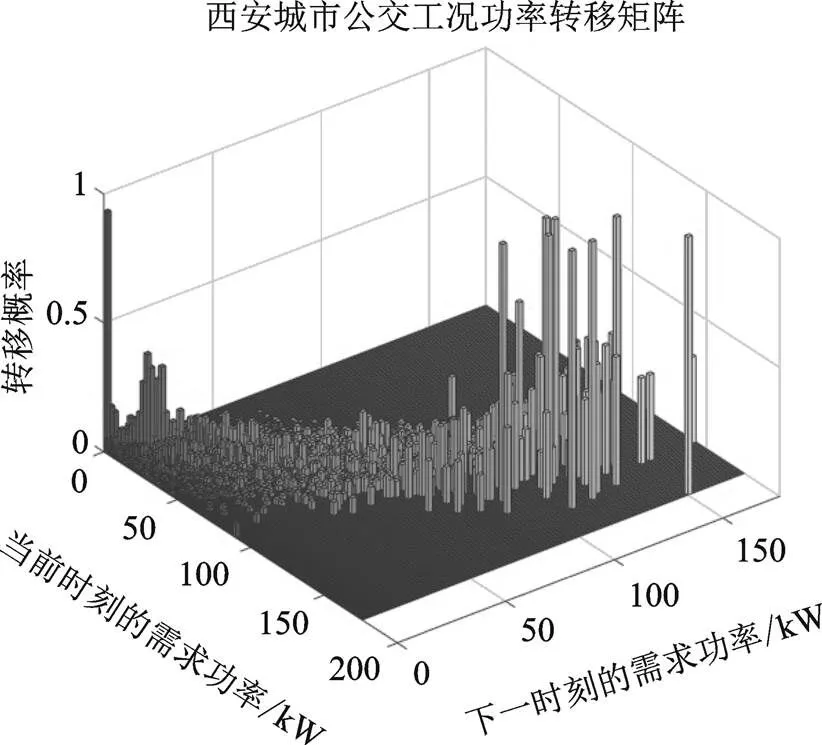
图5 功率转移概率矩阵
利用Matlab使用蒙特卡洛模拟法,基于得到的转移概率矩阵,在每一轮训练之前生成与训练工况长度相等的随机功率序列,用于训练强化学习值函数,从而大大的丰富样本量,改善训练结果。
2.2 Q学习算法模型
Q学习是与环境无关的基于数值迭代的动态规划算法,把被控对象看成智能体,创建表示值函数的表,根据此时的状态,在表中找到所对应最大值的最优动作,并计算得到下一时刻状态s+1和与环境进行交互得到的奖励值,之后对表进行更新。Q学习算法的核心是构建表,本文针对能量管理策略研究,以EGU单元输出功率egu为控制变量,以需求功率r和电池荷电状态为状态变量
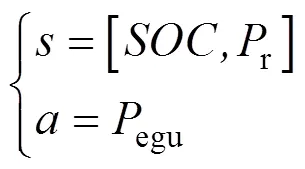
而值函数的更新公式如式(6)所示[4]
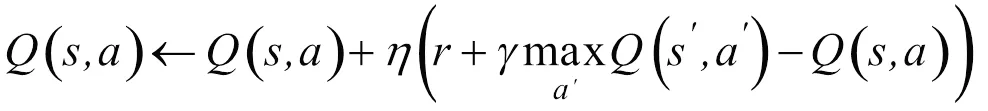
式中,为学习率,决定了此次训练的误差有多少要被学习,本文选择0.012;是未来的奖励对现在的影响因子,越大表示越注重未来的利益,本文选择0.9。
为了防止训练过早的陷入局部最优,使用贪心策略选择动作,智能体以1-的概率选择最大化值的动作,而以的概率选择随机动作,开始训练时较大,之后不断减小直到为0。
奖励函数是衡量每一步动作优劣的关键,PHEV能量管理的目的,是使综合能耗最小化,所以使用的电耗成本和油耗成本组成目标函数,奖励函数为目标函数的倒数[7]
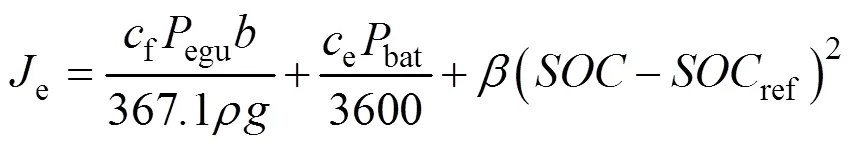
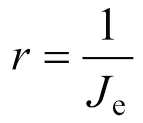
式中,bat为电池实际消耗的功率,因为内阻的存在,实际消耗的功率要大于需求电池功率b;f为燃气价格,取3.7元/m3;e为电价,取0.8元/kWh;为气体密度,取0.717 kg/m3;为重力加速度;ref是期望末值,取0.3;为权重系数,取1。
仿真过程中还要考虑动力系统物理限制,如式(9)所示
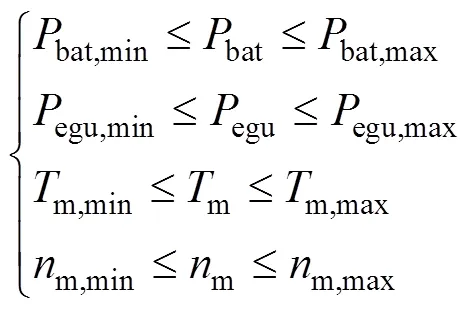
式中,m为电机输出转速;m为电机输出转矩,max和min分别对应了上下边界。
最终,当值平均误差收敛到期望值,或达到最大训练循环后,训练结束,用得到的表对测试工况进行能量分配仿真,得到最优控制序列
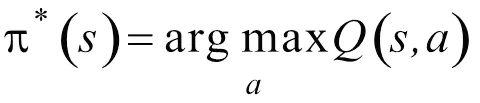
3 CD-CS策略与DP策略构建
3.1 CD-CS策略
CD-CS策略是一种根据工程师经验提出的基于规则的控制策略[8],算法简单,控制速度快,可以实现实时应用,但因为策略过于简单,能耗效果差。
具体的控制过程为,根据电池荷电状态来控制发动机的启动与停止,当较高时,发动机关闭,所有的需求功率均由电池提供,直到电池的降低到最低阈值0.3,为了保证电池不要过放电,发动机启动,按照恒定的70 kW向外输出功率,当上升至设定的阈值上限0.35以后,发动机关闭,功率继续由电池提供。
3.2 DP能量管理策略
动态规划算法理论上能够得到全局最优的控制效果,但是需要预先知道工况,所以无法实时应用,本文使用先逆向求解,在正向寻优的方法来实现。结果用来评估提出的MC-Q算法的优劣。
把电池作为状态变量,离散化之后逆向求解每个时刻不同对应的最优控制变量egu,最后正向获得最优控制序列,逆向递归方程如式(11)所示。
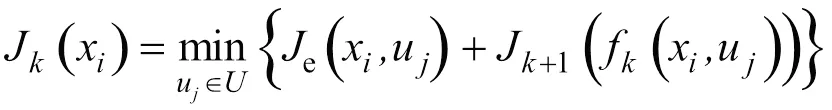
式中,为当前时刻;u为第个EGU功率点;x为第个离散点;为egu的集合;f(x.u)为当前状态变量为x且控制变量为u时得到的第+1步的;e为式(7)所示的目标函数;J(x)是为x时由第步到最后一步的累计最小成本。优化过程同样需要满足如式(9)所示的物理约束。
4 仿真分析
图6是仿真过程中每一轮循环后表与前一轮的偏差值,体现了训练的收敛过程,可以看出在前100轮循环中,表的差值快速下降,即模型快速趋于收敛,又因为训练工况是根据概率矩阵随机生成的,所以表不会完全收敛,而是在较低的水平上下波动,防止了训练过早的陷入局部最优,丰富了训练结果。
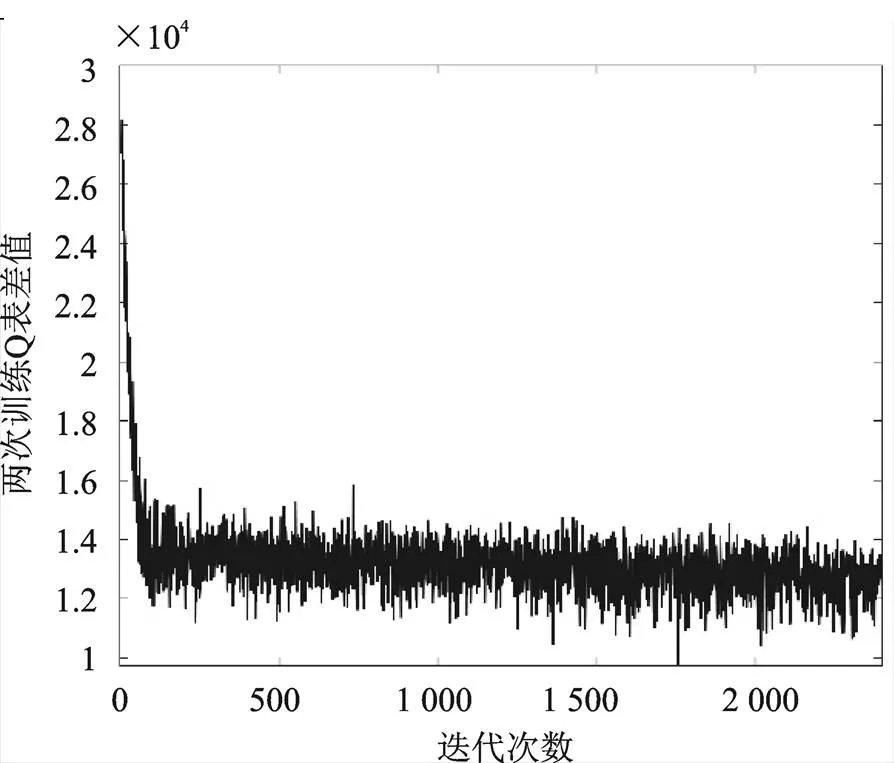
图6 Q表差值
基于前文给出的测试工况,分别使用CD-CS策略、DP策略和所提出的基于马尔科夫链的Q强化学习(MC-Q)策略进行仿真比较,初始值取0.9。变化曲线如图7所示,EGU单元输出功率如图8所示,表1为三种控制策略的成本对比。
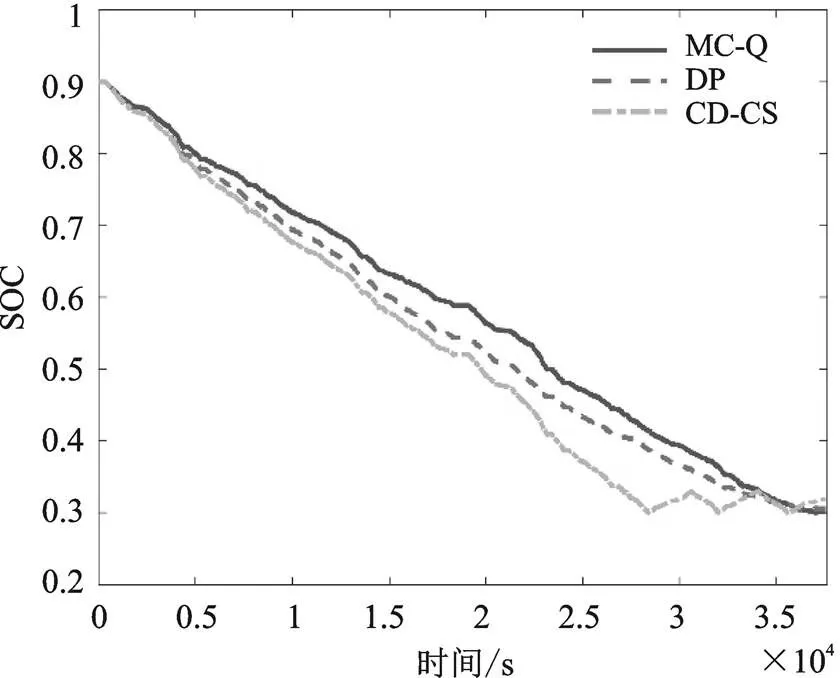
图7 SOC变化曲线对比
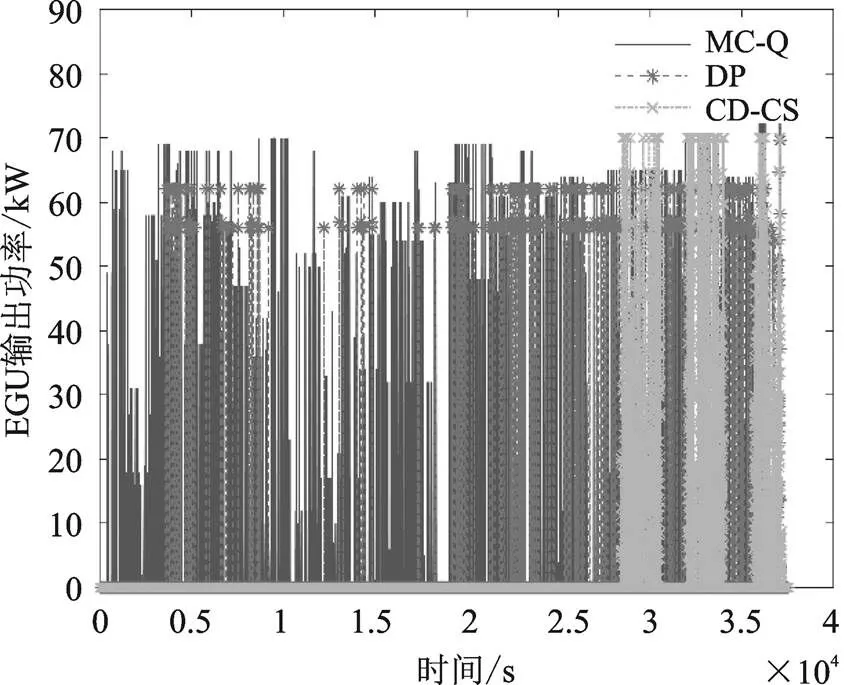
图8 EGU输出功率
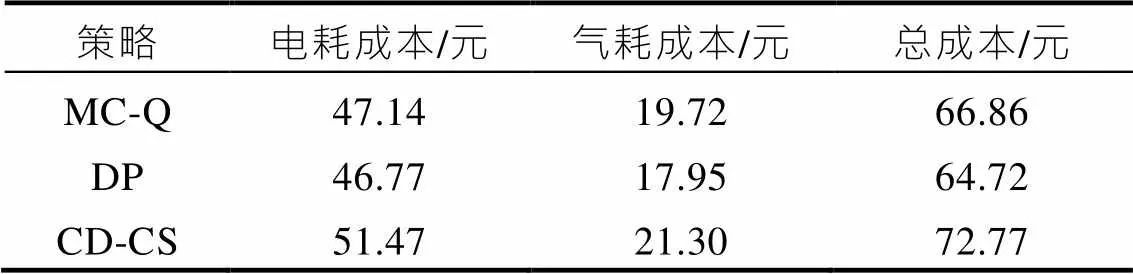
表1 不同策略能耗成本对比
从变化曲线可以看出,三种控制策略最终都达到了期望的最低值0.3左右,但路径不同。结合图5可知,三种控制策略能量的分配过程完全不同,而DP策略因为是全局优化策略,理论上能得到最优的能量分配结果,所以能耗成本最低。而本文所提出的MC-Q策略能耗明显的优于传统的基于规则的CD-CS策略,总成本降低了8.1%,而相比DP策略总成本只略微增长也保持了线性下降,且可实现实时应用。
5 结论
根据仿真结果可知,本文所提出的基于马尔科夫链的Q强化学习能量管理算法,相比传统基于规则的控制策略,在140 km的西安市城市工况下,可以使电耗和能耗组成的总成本降低8元,而相比动态规划得出的全局最优结果,能耗成本只提升了1.9元,且具有一定的鲁棒性,可以根据以往工况训练并且实现在固定线路上实时应用,具有一定的推广意义。
[1] 尹燕莉,张刘锋,周亚伟,等.基于Q学习的纯电动重型商用车智能换挡控制策略研究[J].重庆理工大学学报(自然科学),2021,35(9):73-82.
[2] 解少博,刘通,李会灵,等.基于马尔科夫链的并联PHEB预测型能量管理策略研究[J].汽车工程,2018, 40(8):871-877,911.
[3] LIU T,WANG B,YANG C L.Online Markov Chain- based Energy Management for a Hybrid Tracked Vehicle with Speedy Q-learning[J],Energy,2018(7): 544-555.
[4] 刘腾.混合动力车辆强化学习能量管理研究[D].北京:北京理工大学,2017.
[5] 张刘锋.基于强化学习的混合动力系统智能化控制方法研究[D].重庆:重庆交通大学,2021.
[6] 张盟阳.基于动态规划的PHEV能耗分析[J].汽车实用技术,2021,46(16):130-133.
[7] 解少博,罗慧冉,张乾坤,等.智能网联混合动力车辆速度规划的多目标协同控制研究[J].汽车工程,2021, 43(7):953-961.
[8] 张思雨,史珊珊.PHEV能量管理策略研究[J].汽车实用技术,2022,47(1):186-188.
Energy Management Strategy of PHEV Based on MC-Q Reinforcement Learning
WANG Huiqing
( School of Automotive Engineering, Chang’an University, Xi’an 710064, China )
The plug-in hybrid is energy efficient, and the energy management strategy among multiple power sources has a great impact on the energy consumption of hybrid vehicles.Taking a run on a fixed line series plug-in hybrid city bus as an example, based on the previous cycles, according to markov theory, the demand for power transformation along with the change of time for the state transition matrix, the random power sequence is generated by probability matrix. Module Q reinforcement learning and training, by using the random power sequenceto realize the energy distribution of the city bus real-time optimization control. Simulation results show that the proposed reinforcement learning energy management algorithm can significantly optimize energy consump- tion compared with the rule control algorithm, and can greatly improve the time efficiency compared with dynamic programming and other global optimization strategies, and realize real-time control.
Plug-in hybrid electric vehicle; Energy management; Reinforcement learning; Transition probability matrix
U469.7
A
1671-7988(2022)24-28-05
U469.7
A
1671-7988(2022)24-28-05
10.16638/j.cnki.1671-7988.2022.024.005
王惠庆(1997—),男,硕士研究生,研究方向为新能源汽车能量管理策略与控制算法,E-mail:2421353 871@qq.com。
