660 MW燃煤锅炉屏式过热器壁温特性数值模拟研究

2023-01-06吕俊复吴玉新张天宇马有福

煤炭学报 2022年11期

王涛，周托，吕俊复，吴玉新，张天宇，马有福

(1.上海理工大学能源与动力工程学院，上海 200093；2.清华大学能源与动力工程系，北京 100084)

煤炭在我国能源结构中一直占有很大的比重，2020年我国能源消费中煤炭的占比仍达到56.8%[1]，煤炭作为我国基础能源的地位，在一段时间内无法改变。随着“双碳”目标的提出，我国能源结构正在逐步低碳化，一方面需要提升传统煤炭的利用效率[2]，另一方面要增加可再生能源的比例。因此，我国燃煤火电机组也不断朝着大容量、高参数发展以提升煤炭利用效率；与此同时，燃煤火电机组也被迫全面参与深度调峰，以便更多的消纳可再生能源。燃煤火电机组蒸汽参数的不断提高以及频繁的深度调峰，使得大型燃煤锅炉的安全、稳定运行面临着更大的挑战，而其中由于热偏差而导致的管壁超温问题尤其重要[3-4]。因此，对于大型燃煤锅炉受热面热偏差和壁温的预测以及控制提出了更高的要求。

燃煤锅炉受热面的热偏差和壁温分布是受到烟气侧和工质侧共同影响的结果，主要包括烟气温度分布、烟气流场、工质在管屏间的分配和工质温度分布等。国内外学者常采用数值模拟的方法对热偏差和壁温进行预测，为了简化计算过程，锅炉受热面常设定为均匀壁温[5-7]、均匀工质温度[8]、均匀热流密度[9]、或将受热面简化为多孔介质[10-12]，这些方法都忽略了烟气侧和工质侧相互耦合的影响关系。近年来，考虑将烟气侧与工质侧的流动传热过程进行耦合计算成为主要的研究方法。俞聪等[13-14]利用Fluent和MATLAB对四角切圆锅炉建立了炉内燃烧和高温受热面管内工质流动的耦合模型，详细阐述了烟气和蒸汽的流动耦合传热过程，能够较为准确地得到受热面的温度分布。金东昊等[15]采用类似的方法利用Fluent和Flownex软件对600 MW墙式对冲锅炉的屏式过热器建立了耦合模型，研究发现低负荷下的屏式过热器管壁超温更显著。目前，控制锅炉受热面热偏差和壁温的主要方法分为2类：改变炉膛燃烧方式和优化高温受热面布置。前者是通过优化燃烧使炉膛出口处烟温分布趋于均匀，主要方法有改变各次风比例[16-17]、改变燃烧器和燃尽风喷口的布置方式[18-19]等。后者是在现有的炉膛出口烟温分布下，重新布置高温受热面，例如将超温管屏布置在烟温较低处[20]、根据烟温分布调节管屏流量分布[21-22]等。

为更加准确的预测大型燃煤锅炉的受热面热偏差及壁温分布特性，需同时考虑烟气侧和工质侧的耦合关系。因此，笔者以某660 MW前后墙旋流对冲煤粉锅炉为对象开展数值模拟，并基于Fluent自带的UDF程序建立了屏式过热器管内、外的耦合传热模型，采用按管内工质流动方向的顺序计算方法，实现了烟气侧与工质侧的传热耦合计算。同时，研究了不同外二次风旋流角度对锅炉屏式过热器热偏差及壁温分布的影响，研究结果对相同类型的锅炉燃烧优化具有借鉴意义。

1 锅炉概况

研究对象为一台660 MW的DG2150/25.4-Ⅱ6型前后墙旋流对冲锅炉。炉膛宽度为22.16 m，炉膛深度为15.46 m，炉膛高度为62.00 m。前后墙燃烧器(DBC-OPCC)分3层布置，每层6个，共计36个燃烧器；前后墙燃烧器上方布置一层燃尽风喷口，共计12个；前后墙燃尽风与最上层燃烧器之间各存在2个侧燃尽风口，共计4个，锅炉几何结构和主要参数如图1和表1所示。燃烧器结构如图2所示。锅炉主要运行参数见表2，煤质参数及低位热值(Qnet,ar)见表3。

图1 锅炉结构以及屏式过热器布置示意Fig.1 Schematic of the boiler structure and thearrangement of the platen superheater

表1 锅炉几何结构参数

图2 燃烧器结构示意Fig.2 Schematic of the burners

表2 锅炉主要运行参数

表3 煤质分析

锅炉的屏式过热器分为前分隔屏过热器和后分隔屏过热器，沿炉宽方向各15片屏，共计30片管屏，各管屏之间的距离为1 370 mm。每片管屏由22根并联管圈组成，管圈外径为52.5 mm，管壁厚度为7.5 mm，如图1所示。

2 数值模拟方法和模型介绍

2.1 网格划分

网格划分采用精度高、收敛速度快的多面体网格，整个炉膛的网格间距为0.15～0.40 m，依次对冷灰斗区域、燃烧器区域、屏式过热器区域、末级过热器区域、末级再热器区域划分网格。由于燃烧器区域、屏式过热器、高温过热器区域为主要的燃烧反应和传热计算区域，故对该区域的网格进行加密处理，经网格无关性验证，采用135万多面体网格，炉膛网格划分如图3所示。

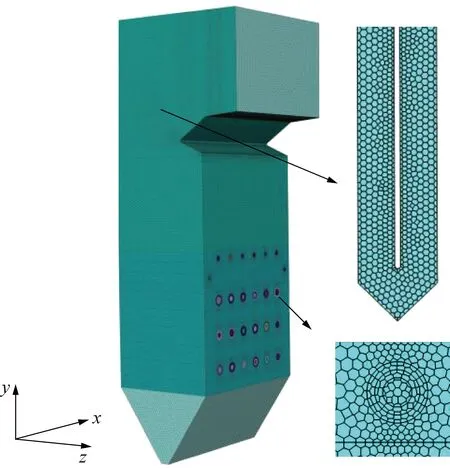
图3 炉膛网格划分Fig.3 Mesh generation of the boiler

2.2 燃烧模型设置

锅炉炉膛内煤粉的燃烧过程非常复杂，涉及湍流流动、化学反应、传热传质等多个方面。本研究中，湍流模型选择带旋流修正的Realizek-ε；燃烧模型采用非预混模型，煤质分析结果见表3；辐射传热模型选择P1模型；挥发分析出模型选择CPD模型；焦炭燃烧模型选择动力学-扩散模型，反应速率参数为0.2 kg/(m2·s·MPa)和79 kJ/mol；气固两相流动模型选择拉格朗日随机轨道模型。煤粉颗粒直径按照Rosin-Rammler方法分布，平均粒径为50 μm，均匀性指数为1.15。

边界条件设置：一次风、内二次风、外二次风、燃尽风均为质量流量入口，具体参数见表4；屏式过热器、末级过热器使用平面代替，初始时设置均匀温度计算，从前到后依次为718，768，818 K；末级再热器由于数量较多，采用多孔介质进行计算；出口为压力出口，设置为-80 Pa。

表4 计算工况运行参数

2.3 受热面计算区域划分以及传热模型

首先需要在屏式过热器划分计算区域，且计算区域的计算方向与蒸汽流动方向一致，本研究将过热器的平面划分为多个正方形的计算区域，每片管屏上3～4根管划分为一个计算区域，共计6个计算区域，如图4所示。以计算区域正中心的坐标代表该计算区域的位置，通过式(1)，(2)进行计算区域坐标的移动。

xi=xi-1+Δxsinθ

(1)

yi=yi-1+Δycosθ

(2)

式中，xi-1和xi分别为第i-1个和第i个计算区域的中心横坐标，m；yi-1和yi分别为第i-1个和第i个计算区域的中心纵坐标，m；Δx和Δy分别为横坐标和纵坐标的变化量，m；θ为计算区域中过热蒸汽的流出方向与y轴正向的夹角。

图4 屏式过热器计算区域划分Fig.4 Schematic of calculation area division

在确定计算区域中心坐标后，通过式(3)～(5)，确定该区域的范围，可根据实际的计算资源进行调节。

xi,L=xi-Δx/2

(3)

xi,R=xi+Δx/2

(4)

yi,down=yi-Δy/2

(5)

yi,up=yi+Δy/2

(6)

式中，下标L，R，down，up分别为计算区域的左边界、右边界、下边界、上边界。

同时，屏式过热器中的蒸汽需满足质量守恒、动量守恒、能量守恒(图5)，计算公式为

m1=m2=…=mi

(7)

(8)

(9)

i=2,3,…,n

(10)

式中，下标i，in，out，G分别为第i个计算区域、计算区域进口、计算区域出口、烟气；m为过热蒸汽质量流量，kg/s；p为压力，Pa；A为管子横截面积，m2；ρ为密度，kg/m3；f为摩擦因数；d为管子内径，m；Δy为计算区域i和i-1的纵坐标距离，m；T为温度，K；K为总传热系数，W/(m2·K)；S为计算区域管子外表面面积，m2；cp为定压比热容，kJ/(kg·K)。

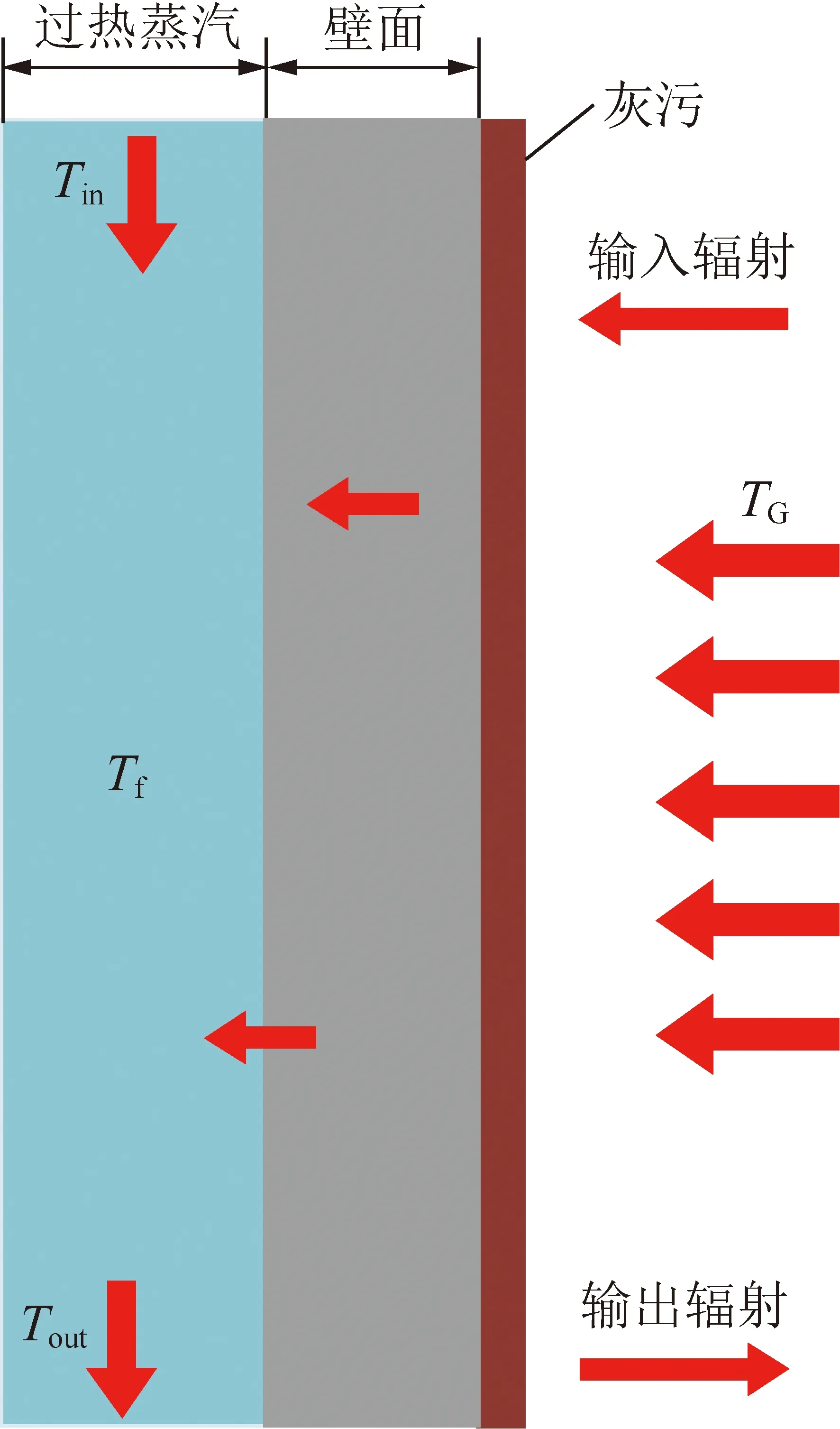
图5 热平衡示意Fig.5 Heat balance of the platen superheater

为了求解能量方程，需得到屏式过热器对流换热量和辐射换热量。因此，分别求得蒸汽对流换热系数hf,i，烟气对流换热系数hG, i，过热器壁面辐射换热系数αi，依次为

(11)

(12)

(13)

式中，下标w，f分别为管子壁面、管内工质；h为对流换热系数，W/(m2·K)；Nu为努塞尔数；λ为导热系数，W/(m2·K)；Re为雷诺数；Pr为普朗特数；D为受热面管子外径，m；α为辐射换热系数，K3；ε为壁面与烟气的系统黑度；σ为Boltzmann常数。

最终计算总换热系数Ki，再通过式(9)计算出第i-1区域的出口温度Tout, i-1，也即第i区域的进口温度Tin, i；然后对进出口温度取算数平均作为该区域的工质温度Tf, i，进而可计算得到外管壁温度Tw, i，即式(15)，(16)。

(14)

Tf,i=(Tin,i+Tout,i)/2

(15)

(16)

式中，δ为壁面厚度，m；R为管外灰污层热阻，m2·K/W。

2.4 耦合方法

在炉膛中，过热器壁面的温度分布主要与烟气的温度分布以及并联管内的流动传热有关。因此，为准确计算过热器受热面壁温，需要准确得到管外烟气的流动参数和管内过热蒸汽的流动参数，具体方法如下：

(1)在Fluent中，将过热器的边界条件先设定为均匀壁温，计算至流场收敛。

(2)在UDF中，首先需确定单元计算区域，由于屏式过热器的网格为多边形，若计算区域与网格完全一致，计算量较大且较难实现。故本研究采用大于多边形的正方形计算区域，并沿x，y方向等距分布，如图4所示。然后改变单元计算区域中心坐标，模拟实现屏式过热器中蒸汽的流动。

(3)在第1个计算区域中，假设入口流量分布是均匀的，把屏过进口温度作为第1个计算区域的入口温度，并假设第1次初始计算的壁面温度，计算屏式过热器管内蒸汽的流动物性参数，即可计算出管内对流换热系数；读取该计算区域的对应网格中的烟气物性，计算出管外对流换热系数和辐射换热系数；最终计算出该计算区域的总换热量。通过能量守恒，可得到管内蒸汽的温度变化，即该单元计算区域的出口温度，该温度作为下一个计算区域的入口温度。

(4)在单元计算区域中，将得到的出口温度与入口温度的平均值作为该计算区域的管内蒸汽温度，写入蒸汽温度文件中。然后，通过管内对流换热系数计算该区域的外管壁温度，写入壁温文件中，同时赋值给Fluent中的过热器网格壁温，计算下一个计算区域。

(5)循环计算步骤2～4，直至屏式过热器出口，然后继续计算燃烧模型。

由于计算量较大，以100步迭代计算一次。当计算至n步后，屏式过热器出口蒸汽温度偏差不超过1 K，即认为达到平衡，停止计算。

整个烟气侧和蒸汽侧传热耦合的计算流程如图6所示。

图6 烟气侧和蒸汽侧传热耦合流程Fig.6 Coupling flow of heat transfer on flue gas and steam

2.5 准确性验证

利用以上模型经初步计算，得到屏式过热器各管屏的出口温度，与实测(旋流角度45°)的各管屏22号管子的测量值进行比较，结果如图7所示。从图7可以看出，测量结果与模拟结果的趋势吻合较好，实测值和模拟值的最大温度差为28 K，相对误差小于4%。

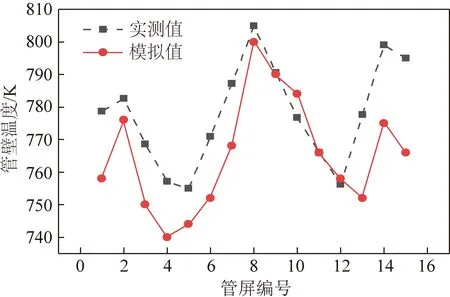
图7 屏式过热器管壁温度实测值和模拟值对比Fig.7 Comparison between test and simulation values ofthe tube wall temperature of the platen superheater

表5为模拟结果与现场测量结果的出口参数对比。现场测量的参数为满负荷运行时的炉膛出口烟温和炉膛出口氧量。由表5可以看出，出口参数的相对误差均小于6%，模拟计算结果在可接受范围内。

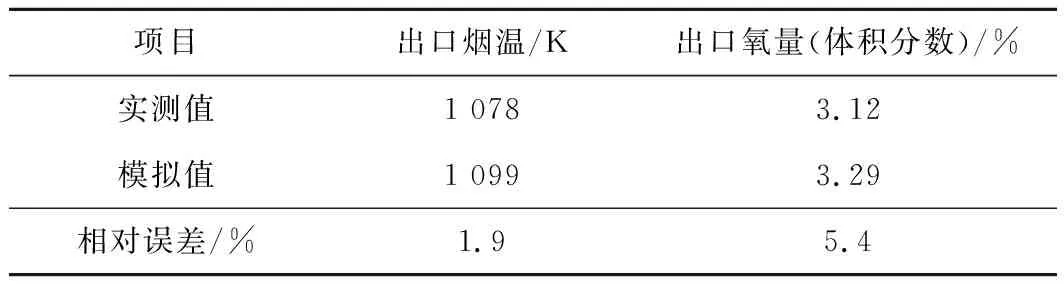
表5 试验结果与模拟结果对比

3 模拟结果与分析

在前后墙旋流对冲锅炉中，旋流燃烧器的旋流角度是影响煤粉燃烧及燃尽的重要因素，旋流角度的改变会显著影响炉膛的烟温分布，进而影响锅炉受热面的传热特性[23-24]。基于此，笔者重点研究了前后墙两侧燃烧器外二风旋流角度的变化(15°～60°)对屏式过热器传热及壁温分布特性的影响(内二次风旋流角度为0°，不做调节)，旋流角度的改变通过改变燃烧器3个流动方向(径向、轴向、切向)的值实现。

3.1 不同旋流角度对炉膛温度分布的影响

不同外二次风旋流角度下炉膛截面的温度分布如图8所示，可以看出，当旋流角度为15°时，旋流角度较小，气流刚性较强，主要向轴向运动，燃烧较为充分。随着旋流角度的增大，气流径向运动增强，轴向运动刚性减弱，并在轴向反向气流的作用下，使燃烧高温区向前后墙扩散，逐渐充满整个炉膛。当旋流角度为60°时，在压力差的作用下，旋流向径向严重扩散，导致炉膛高温区向燃烧器出口和水冷壁靠近，容易发生结渣且存在安全隐患[25]。

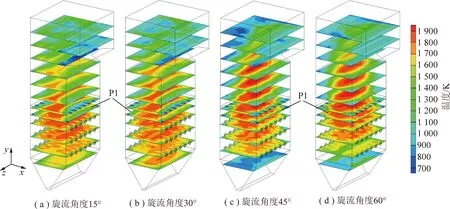
图8 不同外二次风旋流角度下炉膛截面温度分布Fig.8 Temperature distributions of boiler under different external secondary air swirl angles

同时，随着外二次风的旋流角度的增加，炉膛火焰温度略有提升，炉膛火焰高度也略有提高。分析认为这是由于高旋流角度下，燃烧区底部的煤粉扰动较弱，煤粉燃烧不剧烈，外二次风延迟与煤粉气流的混合，燃烧区上移，又由于上层燃烧器和燃尽风中氧量进入炉膛，使煤粉气流剧烈燃烧，温度上升。

3.2 不同旋流角度对受热面热负荷分布的影响

图9为不同旋流角度下屏式过热器的热流密度分布。由图9可知，屏式过热器底部热流密度较高，主要受到复杂烟温的影响，因此与烟温分布基本一致[26]。同时，对比不同外二次风旋流角度的结果，当旋流角度为15°和30°时，热流密度分布呈现“两端高，中间低”的趋势；当旋流角度增大到45°时，热流密度分布呈现“两端低，中间高”的趋势，且随着旋流角度的继续增加，该趋势略有加剧。观察图8中P1处，炉膛截面火焰由“两边宽、中间窄”的沙漏型随旋流角度增大变为“两边窄、中间低”的球形。分析认为，旋流角度较小时，气流刚性强，在侧燃尽风区域，轴向运动的燃尽风与上升运动的煤粉气流混合，2者气流刚性相近，能够较好的混合，燃烧剧烈；但旋流角度变大后，炉膛高度方向上的烟气运动较为缓慢，与刚性较强的侧燃尽风难以混合，侧燃尽风对烟气的降温作用较强，且燃烧不剧烈，故该处温度相对较低。

图9 不同外二次风旋流角度下屏式过热器热流密度分布Fig.9 Heat flux distributions of platen superheater under different external secondary air swirl angles

3.3 不同旋流角度对受热面温度分布的影响

图10为不同旋流角度下受热面的温度分布。可以发现，受热面的高温区域与受热面的高热流密度区域基本一致。由式(16)可知，壁温主要受到热流密度、管内工质温度、管内对流换热系数、管子本身物性参数共同影响。由于受热面底部的热流密度远高于受热面出口，故底部的壁面温度相对较大。对比不同的外二次风旋流角度，随着旋流角度的增大，受热面的温度分布与热流密度分布呈现相同变化趋势，由“两端高、中间低”向“两端低、中间高”变化。

图10 不同外二次风旋流角度下屏式过热器温度分布Fig.10 Temperature distributions of platen superheater under different external secondary air swirl angles

图11为不同外二次风旋流角度屏式过热器每片管屏底部的最高管壁温度。当旋流角度为15°和30°时，屏式过热器的最高管壁温度出现在两端，分别为905，918 K；当旋流角度为45°和60°时，屏式过热器的最高管壁温度出现在中部，分别为945，965 K。而屏式过热器的材料为SA-213TP347H，最大的允许管壁温度为923 K，故旋流角度过大时，管壁存在超温危险，当旋流角度在30°以下时，屏式过热器的管壁温度分布较为安全。

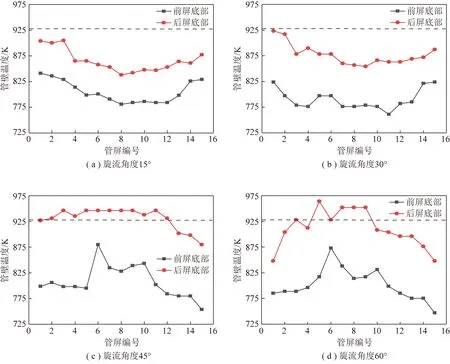
图11 不同外二次风旋流角度下前屏底部和后屏底部温度分布Fig.11 Temperature distributions of the bottom of front platen and rear platen underdifferent external secondary air swirl angles

图12为屏式过热器后屏出口壁温分布。对于不同管屏，出口壁温分布主要受到受热面热流密度的影响，且是温度累积的结果，故温度分布趋势与热流密度分布趋势一致，低旋流角度时“两端高、中间低”，高旋流角度时“两端低、中间高”。不同旋流角度下，屏式过热器出口壁温最大值与最小值相差60～80 K，存在较大的不均匀性。

图12 不同外二次风旋流角度下后屏过热器的出口壁温分布Fig.12 Temperature distributions of the outlet of rear platen superheater under different external secondary air swirl angles

对同一管屏，由于外圈管子长度较长，吸热量大，大部分外部管圈的壁温略大于内部管圈的壁温。