考虑竞争关系的重大工程多主体平行施工资源共享行为研究
2023-01-06刘娜娜周国华
刘娜娜,周国华
(西南交通大学 经济管理学院,四川 成都 610031)
重大基础设施工程指投资规模大、环境复杂、建设与生命周期长、技术先进、主要为社会提供长久性基础构筑物,能够对国家经济、社会、政治、科技等多个领域产生深刻影响的一类工程,简称重大工程[1-2],如港珠澳大桥、三峡工程、青藏铁路等。考虑到建设环境的复杂性以及规模宏大、生命周期长等特征,重大工程建设一般会由多个施工主体进行施工活动[3]。比如在建的郑万高铁兴山隧道工程,就是将一条隧道分为两个标段,由不同的施工单位进行平行施工,以达到缩短施工工期的目的。在复杂环境之下面临众多的不确定性因素,承包商在施工过程中难以避免会出现施工资源短缺的情况,这不仅会拖延施工进度,导致施工总工期延迟,也会增加施工总成本。为了满足工程工期要求,提高资源利用率,承包商之间进行合作是减少项目因资源缺乏而造成工期延误和收益损失的有效途径[4]。
关于共享资源相关研究,多数围绕如何进行共享资源组织与优化设计展开[5]。对于施工资源共享,主要集中在多项目资源冲突协调机制[6-7]和资源联合管理[8-10]等方面。多项目资源冲突问题一般由资源需求方或者业主组织协商来解决,以满足所有项目工期要求。对于资源联合管理,Asgari等[8]发现通过承包商之间的合作能够为各方带来增量收益,并采用Shapley值法对承包商之间资源共享增量收益进行分配。Hafezalkotob等[9]针对重大工程项目中承包商合作过程中时间和多资源管理问题,在文献[8]模型的基础上考虑了资源共享过程中多种成本,提出基于合作博弈论的时间-多资源权衡模型,结果表明通过资源共享承包商可以获得更高的利润,而且Shapley值法、最大-最小核心法和等利润法能够将额外的合作利润公平分配给承包商。王红卫等[10]针对重大工程承包商资源共享问题建立资源需求方为主导者,资源提供方为跟随者的Stackelberg主从博弈模型,并分析业主激励及施工成本对模型均衡解的影响。在实际重大工程中,业主为了促使整个项目更快完成,会委托多个施工主体进行施工,并且不同施工主体之间可能会存在竞争关系,如高速铁路、高速公路等工程建设中,当平行施工主体的一方进度较快,在完成自身标段工程量时可以继续进行施工。考虑到平行施工主体之间的竞争关系,本文在文献[10]相关研究的基础上对重大工程多主体的资源共享行为进行研究,这也是与其他学者相关研究的重点区别。
以往对于竞争与合作的研究偏向于采用二分法进行彻底孤立研究,为了使参与者行为模式更贴近现实,近年来组织间既存在竞争又存在合作关系即“竞合”逐渐引起诸多学者密切关注。郭红莲等[11]为了追求供应链的高效率,研究了M个供应商、1个制造商、N个经销商的三级供应链竞争合作博弈协调模型。王娜等[12]通过构建竞争与合作的博弈模型,分析碳税对制造/再制造决策的影响。Bernstein等[13]对零售商间的竞合博弈策略展开研究。王文杰等[14]研究平台存在不同竞争强度下众包物流配送服务的最优定价策略。许丽霞等[15]应用竞合博弈研究由两个制造商和一个零售商构成供应链的价格契约问题,分析竞争强度对竞争与合作关系的影响。肖旦等[16]在随机需求下讨论库存技术共享零售商联合采购联盟的竞合博弈策略。随后肖旦等[17]通过建立联盟成员间竞合博弈模型研究零售商的改良技术共享下改良品的联合采购问题。以往对于竞合关系的研究主要集中在供应链方面,在整个博弈关系中虽然既有竞争又有合作,但是竞争与合作是分阶段进行分析研究,本文针对重大工程领域施工方之间的工程量竞争与资源共享合作关系进行研究,是一个典型的竞争与合作同时存在的竞合问题。
本文以重大工程多标段平行施工中的不同施工主体为研究对象,引入工程量竞争机制(一方施工完成可以继续施工,直至双方共同将整个工程建设完成),分析施工主体之间工程量不存在竞争关系和工程量存在竞争关系两种模式下施工主体的资源共享行为策略,即资源提供方对资源共享量以及资源需求方对资源价格的最佳反应,得出不同模式均衡状态下各施工主体的利润,并且通过数值模拟形象地展示业主奖惩激励措施、共享资源利用率、施工成本系数等因素对均衡结果的影响,为重大工程平行施工主体资源共享行为策略选择提供指导建议。
1 问题描述与基本假设
1.1 问题描述
对于重大工程而言,尤其是以隧道工程为代表的地下交通建设工程,当面临的工程环境较为复杂时,施工现场资源短缺时常发生,不同施工主体之间通过资源共享合作能够在一定程度上解决资源短缺问题。假设业主将重大工程项目分为两个标段,标段一委托于施工方A、标段二委托于施工方B进行工程建设。如图1所示,当施工过程中出现资源短缺时,资源需求方可以与另外施工方进行资源共享协商,首先由资源需求方A提出共享资源价格P,然后资源提供方B在主体A所提出共享价格的基础上决定资源共享量M。此资源共享合作问题可以用Stackelberg主从博弈模型进行体现[10]。并且,业主采用进度奖惩措施对施工方进行激励,即工期提前的施工方将得到奖金,工期延期的施工方将得到罚金。

图1 业主及施工方之间的关系Figure 1 The relationship among owner and contractors
实际工程项目中,为了使整个项目工期更优,业主有时会在施工主体之间引入工程量竞争机制,即一方先完成所在标段工程量可以继续向前施工,直至双方共同完成工程项目建设。如图2所示,合同中标段一的工程量为OA,标段二的工程量为AD,当按照合同施工速度都没有发生变化时,将在E点完成项目,双方计划工期都为t0。当某一施工方施工速度增加时,即对应图中的F转折点,无竞争机制下项目依然在E点完成,竞争机制下项目将在G点完成,因此通过竞争机制设计能够使项目总工期减少t0-t2,此时两施工方对应的工程量分别为OB、BD。同样地,当某一施工方施工速度降低时,即对应图中的H转折点,无竞争机制下项目将在J点完成,而竞争机制下项目在I点完成,因此通过竞争机制设计能够使项目总工期减少t4-t3,此时两施工方对应的工程量分别为OC、CD。工程进度是实际工程中评价项目效率的一个非常重要的因素[18],这也是实际工程中业主会选择增加竞争机制的原因。

图2 竞争机制下重大工程多标段平行施工关系Figure 2 Multi-bid parallel construction of major projects under competition mechanism
1.2 基本假设
1) 重大工程各标段合同采用单价合同,合同价格=工程量×综合单价。在非竞争机制下,合同价格为常数,而在竞争机制下,由于工程量存在变化,因此合同价不确定,受双方工程进度的影响。假设两标段的单价都为P0,标段一的工程量为Wa,标段二的工程量为Wb(以下标a、b区分两施工方),则非竞争机制下各标段合同价格Ea=P0Wa,Eb=P0Wb;竞争机制下各标段合同价格
2) 假设两个标段平行施工的计划工期相同,记为t0,对施工方A、B来说,租赁前计划工期记为ta1=tb1=t0,资源共享后的工期分别为ta2、tb2(以下标1、2区分资源共享前和资源共享后) 。根据文献[10],施工主体之间设备共享对各自承担工程进度具有影响,假设施工方A、B的计划设备分别为ma、mb台,设备的台班产量都为D,设备资源在共享后其利用率得到提高,台班产量由D变为 λD,其中λ>1,为资源利用率系数。由于设备租赁前后工程量不发生变化,则ta1maD=ta2maD+MλD,可以得出施工方A在资源接收前后工期变化,Δta=ta1-ta2=,承包商A的工期会提前。对于施工方B来说,tb1mbD=tb2mbD-MD,可以得出施工方B在资源共享前后工期的变化,则承包商B的工期会拖延。
3) 线性激励为最为常见的激励方式,当工期提前会获得单位工期奖励,工期延迟则受到罚金处罚。假设施工方所获得的奖惩都与其工期提前或延期的时间呈线性相关,且工期提前和工期延迟受到的单位奖励和罚金相同,即AI=I(t1-t2),其中,I>0为业主激励系数。
4) 项目施工成本是项目工期的分段线性凸函数[19]。本文参考文献[10],利用二次多项式函数C(t)=cγt2+cβt+cα描述成本与工期的关系,cα、cβ、cγ为项目工期成本系数,其中,cα为常数,且cα>0,cβ<0,cγ>0。假设承包商A、B的项目工期成本系数相同,则C(ta)=cγta2+cβta+cα;C(tb)=cγtb2+cβtb+cα。建筑施工中生命成本也是施工成本中重要的一部分[20],由于同一项目资源共享前后生命成本基本不发生变化,因此本文假设其为0。
2 模型构建与求解
2.1 无竞争机制下博弈模型构建与求解
在施工主体A和B资源共享的Stackelberg博弈过程中,首先提出共享资源价格的资源需求方A是博弈过程中的领导者;根据A的决策选择资源共享量的资源提供方B是博弈过程中的追随者。各施工主体都以最大化自身的收益为目标,因此可以构建双方收益函数如下。
施工主体A、B无资源共享的收益函数为
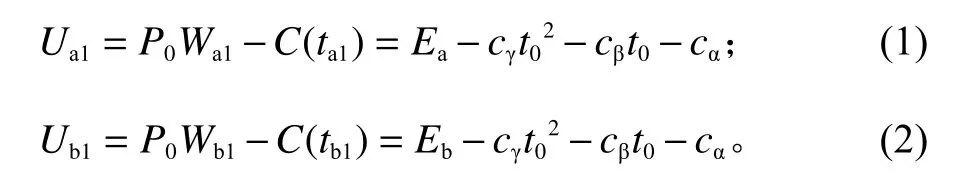
施工主体A、B之间进行资源共享的收益函数为


出于简洁化,令ϕ=I+2cγt0+cβ。为保证共享资源价格为正,此时应满足ϕ=I+2cγt0+aβ>0。
将P*代入式(5),可得
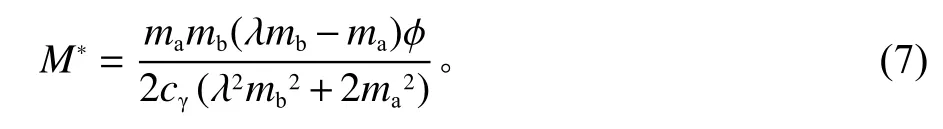
为保证资源共享量为正,此时应满足λmb>ma。
将无资源共享作为参照状态,因此以资源共享与无资源共享收益差值表示通过资源共享获得的收益。进一步可以求得,施工方A、施工方B和整个系统通过资源共享所获得的最优收益差值为

2.2 竞争机制下博弈模型构建与求解

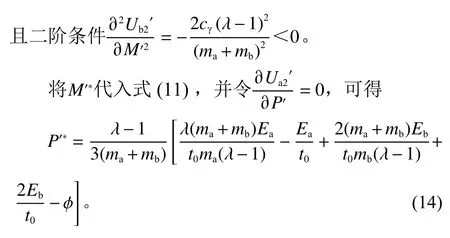
将P*代入式(13),可以求得最优资源共享量为
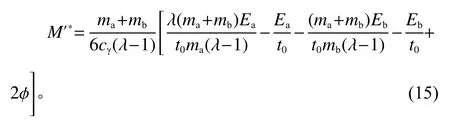
因此可以求出最优策略下重大工程项目工期压缩时间为
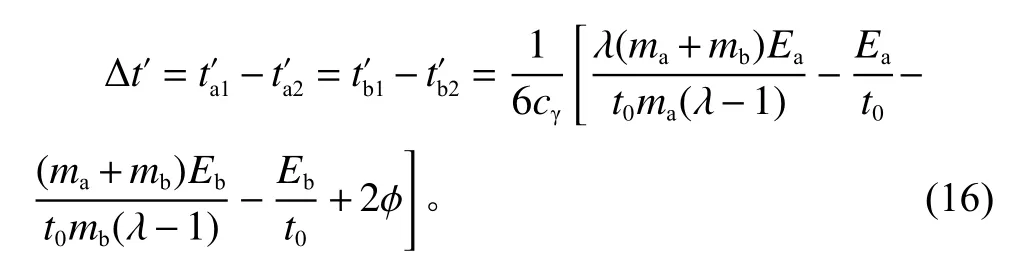
进一步可以求得,竞争机制下施工方A、施工方B、整个系统通过资源共享所获得的最优收益差值为

3 结果讨论与分析
归纳上述无竞争机制和有竞争机制两种情境下的均衡结果,可以得到表1。从表1中结果分析能够得到以下命题。

表1 不同机制下的均衡结果Table 1 Equilibrium results under different mechanisms
命题1不论是竞争机制还是无竞争机制下,施工主体采取资源共享行为都比不采取资源共享行为所获的最优收益大。
证明无竞争机制下施工方A采取资源共享策略比不采取资源共享策略的利益差值为ΔUa=Ua2-因为cγ>0,所以ΔUa>0,同样可得ΔUb>0。
竞争机制下采取资源共享策略比不采取资源共享策略的利益差值为
问题情境教学体现了“教为主导、学为主体”的指导思想。教学活动是师生的双边活动,既要体现教师的主导作用,也要体现学生的主体作用,二者缺一不可。问题情境就是一种较好实现二者有机统一的教学方式,教师通过提出问题,做深入浅出的引导,让教师的“主导”作用充分体现出来。同时,通过提出问题和创设意境,启发学生积极联想和思考,让学生讨论和发言,积极探讨和解决问题。师生地位平等,摒弃了传统师生不平等的关系及教师所讲授内容的“绝对权威”,真正实现了教学上的民主。

同样可得ΔUb′>0。
证毕。
命题1表明,如果施工主体之间能够进行资源共享,各主体的最优战略行为是采取资源共享行为,通过资源共享能够实现协同合作达到互利共赢。
命题2不论是竞争机制还是无竞争机制下,施工主体A作为资源接收者增加的收益都要优于施工主体B作为资源分享者增加的收益,并且无竞争机制下ΔUa=2ΔUb,竞争机制下ΔUa′=3ΔUb′。

证毕。
命题2表明,作为资源需求者的施工主体A始终比作为资源分享者的施工主体B获得更多的收益增加值,这是因为施工主体A在博弈过程中处于主导地位,其具有先动优势。并且,在竞争机制中,施工主体A在获得更多资源后能够加快施工进度进而获得更多的工程量,由于工程量变化使得双方资源共享增加的收益产生更大的差距。
命题3无竞争机制下,施工主体之间进行资源共享能够使资源接收方施工主体的工期压缩,使资源共享方施工主体的工期得到拖延,而总工期将拖延;竞争机制下,施工主体之间进行资源共享能够使双方的工期都得到压缩,总工期将提前
证明无竞争机制下,
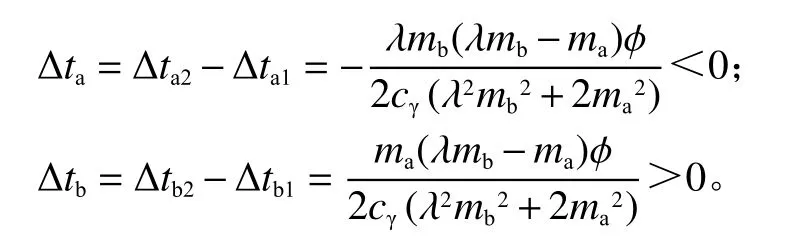
竞争机制下,

证毕。
命题3表明,无竞争机制和有竞争机制两种合同模式下,虽然都能够为各施工主体带来利益增加,但施工主体之间进行的资源共享行为对业主来说会产生不同的效果,无竞争机制下会增加整个项目的工期,竞争机制能够缩短整个项目的工期。
无竞争机制下,各决策变量的影响因素主要有激励系数、共享资源效率系数、施工成本系数等;竞争机制下,各决策变量的影响因素不仅受到激系数、共享资源效率系数、施工成本系数等影响,还受到各方工程量大小的影响。各主要影响因素对决策变量产生什么样的影响,将会通过数值分析进行说明。
4 数值分析
前文已对承包商之间具有工程量竞争和不具有竞争两种机制下的设备资源共享行为进行了理论分析,为了更好地说明不同机制下业主的激励情况、共享资源效率、施工方的成本系数对承包商资源共享行为、承包商收益等的影响,本部分以某一项目为例,进行数值分析。假设某大型隧道工程分为两个标段,由承包商A、B分别负责施工,两标段的计划工期相同t0=2000 d,采用单价合同,标段一的合同价Ea=8000万元,标段二的合同价Eb=10000万元。承包商A拥有某类型工程设备资源ma=80台,承包商B拥有同类设备资源mb=100台。业主对工程进度进行激励,激励系数I=1 万元/d,即提前1 d奖励1万元,延迟一 d惩罚1万元。假设成本系数cγ=0.05,cβ=-200,cα=3000;共享资源效率λ=1.5。
4.1 激励系数对模型均衡解的影响
1) 激励系数对资源共享均衡价格的影响。从图3的数值模拟结果能够发现,无竞争机制下,随着业主激励系数I的增大,平行施工承包商之间资源共享的均衡价格P呈递增趋势;竞争机制下,随着业主激励系数I的增大,平行施工承包商之间资源共享的均衡价格P呈递减趋势;存在一个临界激励系数,当业主激励小于此临界值时,竞争机制下均衡价格大于无竞争机制下均衡价格,当业主激励大于此临界值时,竞争机制下均衡价格小于无竞争机制下均衡价格;无竞争机制下激励系数对均衡价格的影响更敏感。
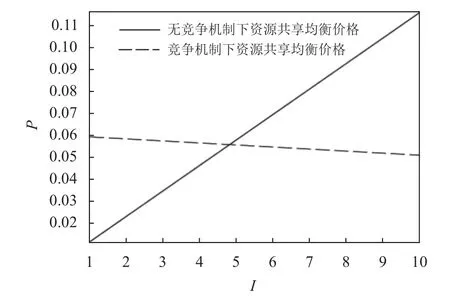
图3 激励系数对资源共享价格的影响Figure 3 The impact of incentive coefficient on the price of resource sharing
2) 激励系数对资源共享量的影响。从图4的数值模拟结果能够发现,随着业主激励系数I的增大,无竞争机制和有竞争机制两种情况下,施工承包商之间资源共享均衡量M都呈递增趋势;竞争机制下的资源共享量始终大于无竞争机制下的资源共享量,并且竞争机制下激励系数对均衡量的影响更大。

图4 激励系数对资源共享量的影响Figure 4 The impact of incentive coefficient on the amount of resource sharing
3) 激励系数对资源共享收益差值的影响。从图5的数值模拟结果能够发现,无竞争机制和有竞争机制两种模式下,随着业主激励系数I的增大,资源提供主体B和资源接收主体A收益差值 ΔU都呈递增趋势;竞争机制下施工方通过资源共享获得的收益差值大于无竞争机制下施工方通过资源共享获得的收益差值;同一种机制下,资源接收主体A的资源共享收益差值始终大于资源提供主体B的资源共享收益差值。

图5 激励系数对资源共享收益差值的影响Figure 5 The impact of incentive coefficient on the profit margin of resource sharing
4.2 共享资源效率对模型均衡解的影响
1) 共享资源效率对资源共享价格的影响。从图6的数值模拟结果能够发现,无竞争机制下,共享资源效率 λ对资源共享均衡价格P的影响不大;竞争机制下,随着共享资源效率 λ的增加,资源共享均衡价格P呈明显递增趋势;随着λ 的增加,竞争机制下资源共享均衡价格始终大于无竞争机制下资源共享均衡价格。

图6 共享资源效率对资源共享价格的影响Figure 6 The impact of resource sharing efficiency on the price of resource sharing
2) 共享资源效率对资源共享量的影响。从图7的数值模拟结果能够发现,无竞争机制下,共享资源效率 λ对资源共享量M的影响不大;竞争机制下,随着共享资源效率 λ的增加,资源共享量M呈递减趋势;随着 λ的增加,竞争机制下资源共享量始终大于无竞争机制下资源共享量。

图7 共享资源效率对资源共享量的影响Figure 7 The impact of resource sharing efficiency on the amount of resource sharing
3) 共享资源效率对资源共享收益差值的影响。从图8的数值模拟结果能够发现,不论施工方之间是否存在竞争机制,共享资源效率 λ对各主体最优资源共享收益差值 ΔU的影响不大。
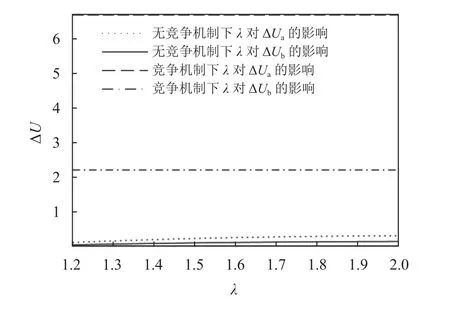
图8 共享资源效率对资源共享收益差值的影响Figure 8 The impact of resource sharing efficiency on the profit margin of resource sharing
4.3 成本系数对模型均衡解的影响
1) 施工成本系数对资源共享价格的影响。从图9的数值模拟结果能够发现,无竞争机制下,成本系数cβ对资源共享的均衡价格P的影响不大,随着成本系数cγ的增大,资源共享的均衡价格P呈递减趋势;竞争机制下,随着成本系数 -cβ减小,cγ增大,资源共享的均衡价格P呈递增趋势;存在临界成本系数函数cγ(cβ),若成本组合(cβ,cγ)满足此函数,两种机制下资源共享均衡价格相同。
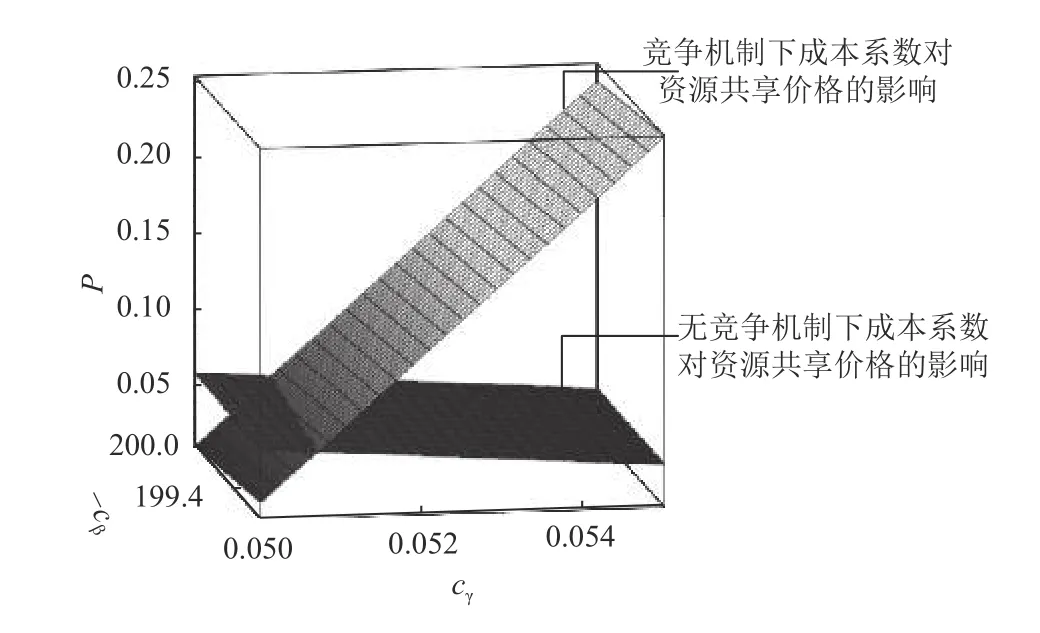
图9 成本系数对资源共享价格的影响Figure 9 The impact of cost factor on the price of resource sharing
2) 施工成本系数对资源量的影响。从图10的数值模拟结果能够发现,无竞争机制下,成本系数cβ对资源共享量M的影响不大,随着成本系数cγ的增大,资源共享量M呈递减趋势;竞争机制下,随着成本系数 -cβ减小,cγ增大,资源共享量M呈递增趋势;随着成本组合(cβ,cγ)的变化,竞争机制下资源共享量始终大于无竞争机制下资源共享量。

图10 成本系数对资源共享量的影响Figure 10 The impact of cost factor on the amount of resource sharing
3) 施工成本系数对资源共享收益差值的影响。从图11的数值模拟结果能够发现,无竞争机制下,成本系数cβ对施工主体资源共享收益差值 ΔU的影响不大,随着成本系数cγ的增大,各主体的资源共享收益差值 ΔU呈递增趋势;竞争机制下,随着成本系数 -cβ减小,cγ增大,各主体资源共享收益差值ΔU呈递增趋势;成本系数变化不改变施工主体资源收益差值大小规律。

图11 成本系数对资源共享收益差值的影响Figure 11 The impact of cost factor on the profit margin of resource sharing
5 结语
重大工程多个主体进行平行施工是业主提高施工效率的一种常见方式,不同主体之间的资源共享行为对整个工程项目建设具有重要的意义,因此受到行业内更多关注。本文在前人研究的基础上引入不同施工主体之间的工程量竞争机制,分别针对重大工程多主体平行施工过程中工程量无竞争机制和有竞争机制两种情境下施工主体间的资源共享行为进行了研究。分别构建了以资源需求方为主导者、资源共享方为跟随者的Stackelberg动态博弈模型,得出两种模式下资源需求方的资源共享价格均衡策略、资源提供方的资源共享量均衡策略以及资源共享为各主体与整个项目带来的收益,通过数值模拟分析业主激励、资源共享效率、成本系数等因素对均衡结果的影响。通过研究得到以下结论。
1) 重大工程平行施工过程中,无论施工主体之间是否存在竞争机制,施工主体之间通过资源共享合作行为都能够获得额外收益;并且资源需求方通过合作所增加的收益大于资源共享方通过资源共享合作所增加的收益。
2) 无竞争机制资源共享均衡状态下,资源接收方的工期得到压缩,资源共享方的工期得到拖延,项目总工期将得到拖延;竞争机制资源共享均衡状态下,各施工方的工期都得到压缩,项目总工期将提前。业主在平行施工的多主体之间引入工程量竞争机制,有利于整个项目工期目标实现。
3) 无竞争机制下,资源共享均衡价格与业主激励系数、共享资源效率呈正相关关系,与成本系数cγ呈负相关关系;资源共享量与业主激励系数呈正相关关系,与施工成本系数cγ呈负相关关系;各主体资源共享收益与业主激励系数、成本系数cγ呈正相关关系。
4) 竞争机制下,资源共享均衡价格与共享资源效率、成本系数cβ、cγ呈正相关关系,与业主激励系数呈负相关关系;资源共享量与业主激励系数、成本系数cβ、cγ呈正相关关系,与共享资源效率呈负相关关系;各主体资源共享收益与业主激励系数、成本系数cγ呈正相关关系。
本文目前将重大工程多主体平行施工过程中所共享的资源限定为施工设备资源,对合作过程中的资源定价以及资源共享量进行了研究,对于其他类型资源,比如人力、资金、知识等资源的共享情况还有待进一步探讨。此外,本文将无资源共享机制作为参考状态,没有考虑项目的不确定性,由于重大工程项目中广泛存在不确定性,下一步可利用鲁棒优化模型或两阶段随机规划等方法对模型进行优化扩展。
