基于工序逻辑关系的关键链缓冲确定方法研究
2023-01-06张俊光武转转
张俊光,武转转
(北京科技大学 经济管理学院,北京 100083)
项目是为创造独特的产品、服务或成果而进行的临时性工作[1],管理者围绕其进度、质量和成本等目标进行项目管理与控制。针对传统管理方法的不足,Goldratt[2]提出一种全新的项目管理方法——关键链项目管理(critical chain project management,CCPM) 。与关键路径法和计划评审技术相比,关键链法能够有效缩短项目工期[3]。
一项针对79个国家的调查显示,CCPM对新产品开发绩效产生的积极影响显著优于传统管理方法[4]。考虑到不确定因素对项目的影响,人们在估计工期时会加入大量的安全时间,但由于不确定因素的存在,安全时间常常被浪费掉。关键链提取安全时间缩短项目工期,并通过引入缓冲吸收项目中的不确定性,提高项目按时完工率,因此缓冲的估计和设置问题是CCPM的核心。CCPM包含3类缓冲:项目缓冲(project buffer,PB)、接驳缓冲(feeding buffer,FB) 以及资源缓冲(resource buffer,RB) 。其中,项目缓冲位于关键链尾部,防止项目完工时间超过计划要求的期限[5];接驳缓冲位于非关键链与关键链的接口处,用来处理非关键链上的不确定性;与前两者不同,资源缓冲通常作为预警标志确保资源按时到位。目前的研究主要集中在项目缓冲部分,本文也围绕项目缓冲进行尺寸确定研究。
1997年,Goldratt[2]提出剪切-粘贴法(cut and paste method,C&PM) 确定缓冲。该方法将关键链上各项工序预计工期的1/2作为安全时间进行提取,并将安全时间的1/2集中在关键链尾部,作为项目缓冲。剪切-粘贴法简单易行,但是可能导致缓冲区设置过大或过小,出现资源浪费或质量问题[6]。基于以上不足,Newbold[7]结合中心极限定理,用根方差法(root square error method,RSEM) 来计算缓冲大小,但是根方差法假设活动之间相互独立,在活动间存在依赖关系的情况下缺乏准确性。
基于两种经典缓冲确定方法,学者们从不同理论角度出发,对关键链缓冲确定方法进行拓展与完善。首先,关键链项目管理在概率论与数理统计理论的基础上,通过分析符合概率分布的各项活动时间,计算缓冲尺寸。褚春超[8]考虑项目的工期分布特点,在工序工期服从对数正态分布的情况下计算项目缓冲。马力等[9]基于根方差方法,提出一种改进型的自适应缓冲设置方法,这种方法不仅有效缩短缓冲长度,而且能避免因缓冲设置不合理产生的资源冲突问题。单汨源等[10]提出一种基于偶然不确定性因素视角的缓冲计算方法,该方法提取因偶然性不确定因素所加入的安全时间来计算缓冲大小。其次,基于模糊理论的项目缓冲计算方法,有利于分析项目中的不确定因素。Long等[11]通过专家估计活动持续时间,基于模糊集的方法来管理非常规项目。翁东风等[12]提出模糊优选理论与动态规划最优化原理相结合的缓冲确定方法,这一方法适用于系统复杂并且专业性强的项目。张俊光等[13]运用熵权法对评价指标进行权重设定,进而确定项目缓冲,这种方法适用于不同项目的进度估计。最后是基于项目属性。Tukel等[14]考虑资源紧张度和网络复杂度因素,但是没有将这两种属性进行综合分析,可能导致缓冲区偏小。Ghoddousi等[15]结合内部风险建立了缓冲确定模型,并考虑多种属性调整缓冲区。黄建文等[16]针对资源柔性因素进行研究,弥补了以往研究在资源约束方面的欠缺。
综上所述,现有的缓冲确定方法基于多种理论出发计算缓冲尺寸,但都是在工序“从结束到开始”的逻辑关系假设条件下进行的研究,没有充分考虑工序间逻辑关系对缓冲确定的影响。因此,本文结合不同工序逻辑关系的特点,进行安全时间的提取和缓冲尺寸的确定,并通过Matlab仿真案例证明本文方法的有效性。本文的创新之处有以下两点。首先,在安全时间的提取部分,考虑因工序逻辑关系产生的工序间时距。根据工艺逻辑关系和组织逻辑关系将时距进行分类,并对具有弹性的时距抽取安全时间,弥补了以往研究假设工序“从结束到开始”相互衔接不考虑时距的缺陷。其次,在缓冲影响因素部分,考虑了不同逻辑关系带来的不同影响,分析了改进资源紧张度、搭接网络复杂度和相邻工序关联度与项目缓冲区大小的联系,对初始安全时间进行调整。
1 缓冲确定模型
1.1 工序逻辑关系分类
相邻工序之间存在不同的逻辑关系,可以分为从开始到开始(STS)、从开始到结束(STF)、从结束到开始(FTS) 和从结束到结束(FTF),如图1~ 4所示。这些逻辑关系按照约束类型不同分为工艺逻辑关系和组织逻辑关系。本文假设相邻两个工序之间只存在以上4种逻辑关系中的一种,不存在两种关系同时存在的混合逻辑关系。
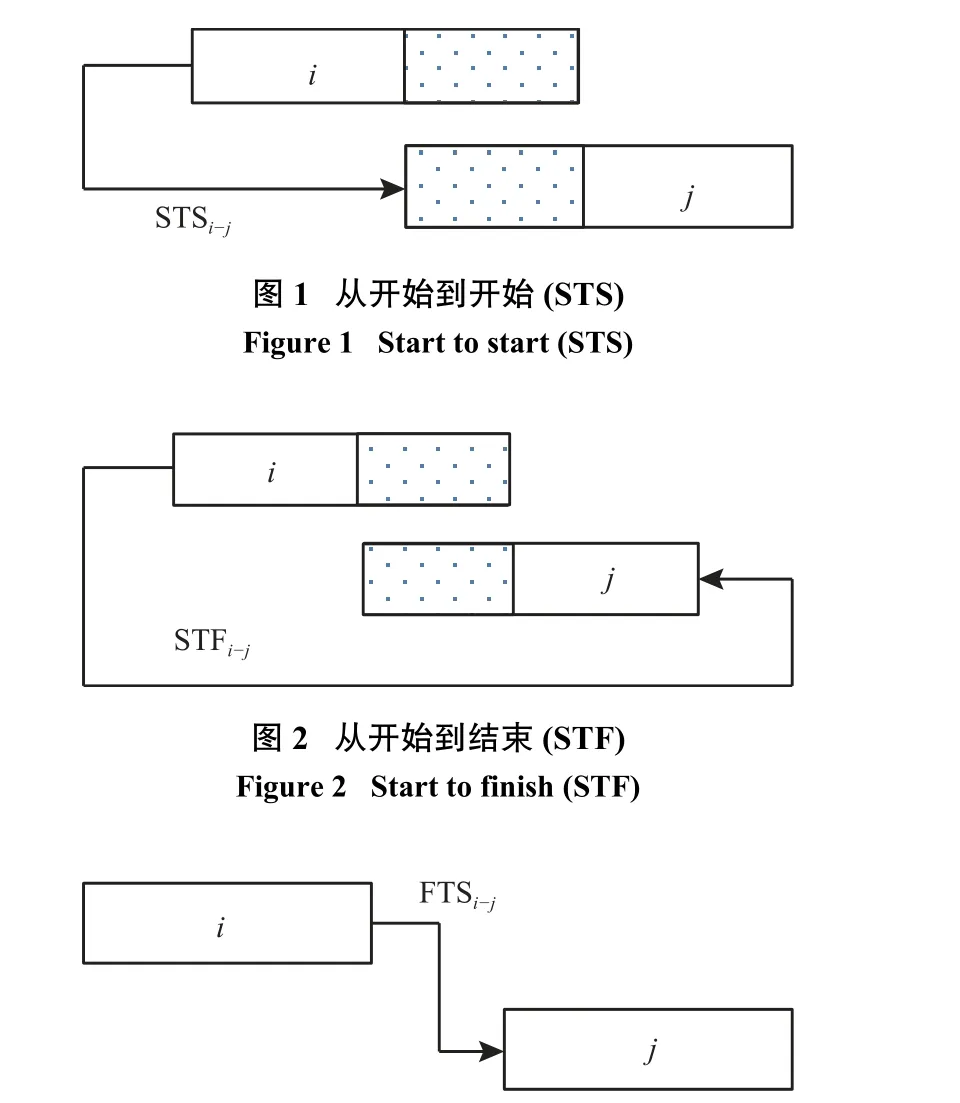
图3 从结束到开始(FTS)Figure 3 Finish to start(FTS)

图4 从结束到结束(FTF)Figure 4 Finish to finish(FTF)
从开始到开始表示工序i开始后至少经过一段间隔时间(STSi-j),工序j才能开始。
从开始到结束表示工序i开始后至少经过一段间隔时间(STFi-j),工序j才能结束。
从结束到开始表示工序i结束后至少经过一段间隔时间(FTSi-j),工序j才能开始。
从结束到结束表示工序i结束后至少经过一段间隔时间(FTFi-j),工序j才能结束。
工艺逻辑关系由工序的工艺确定,只要工艺不变,这种逻辑关系就不会改变。组织逻辑关系则是由实施工序的组织方式决定的。通常情况下,为了保证项目质量水平,工艺逻辑关系不能随便改变;而组织逻辑关系不是由项目本身决定,可以随着工序实施条件和人为组织方式的变化而变化。因此,工艺逻辑关系属于固定逻辑关系,而组织逻辑关系属于软逻辑关系[17]。
1.2 安全时间估计
在预估项目工序工期时,人们通过加入大量的安全时间来吸收不确定性,保障项目能够按时完工。如图5所示,Goldratt[2]将90%的概率完工时间与50%的概率完工时间之间的差值定义为工序安全时间。

图5 工序工期对数正态分布图Figure 5 Lognormal distribution of active duration
本文在以往研究的基础上,考虑工序间不同逻辑关系对项目工期的影响。由逻辑关系产生的工序间时距只消耗时间,不占用资源,类似于项目中的虚工序。由于这些虚工序的存在,工序之间不再只有前后衔接的情况,还包括相互搭接、前后有间隔的情况。显然,在计算项目总工期时,不能直接将关键链上各个工序的工期简单地相加,而要在工序工期总和的基础上加上工序间的间隔时间,减去搭接重叠部分的时间。因此,本文从两方面入手,按照工序工期估计值和逻辑关系特点对工序预期工期以及逻辑时距分别提取安全时间,以提高工作效率,缩短项目总工期。
在传统的PERT项目管理方法中,每个工序给出3个工期估计值,即乐观时间(a)、最可能时间(m) 和悲观时间(b) 。本文采用PERT法中的乐观时间(a) 来估计项目工序时间。因此,bi中应提取的安全时间为

工序间的逻辑关系分为工艺逻辑关系和组织逻辑关系两类,即固定逻辑关系和软逻辑关系。这两类逻辑关系所产生的工序间时距的弹性程度存在差异。
1) 由于固定逻辑关系所产生的工序间时距属于刚性时距,持续时间不可以压缩或延长,只可能按照预定的时间进行。刚性时间没有任何缩短的余地,因此具有刚性约束的时距无法抽取安全时间。
2) 而由软逻辑关系所产生的工序间时距属于弹性时距,可以通过分析与计算合理缩短时距,适当提取安全时间,进一步缩短项目工期。从工序间的柔性时距提取出的安全时间为

1.3 缓冲尺寸影响因素分析
1) 改进资源紧张度。
考虑资源约束对项目工期的影响,是关键链法与其他经典方法相比尤为显著的特点之一。链路中某工序的资源使用量越接近其资源可用量时,项目延误的风险就越大,这时,应该用足够大的缓冲区来吸收这种延迟风险。除了考虑使用量与可提供量之外,本文参考物理学中冲量的定义与表达,对资源紧张度进行改进计算。
经典力学中的冲量I是一个过程量,由作用在物体上的力F与其作用时间t相乘确定,表示作用力在物体上的累积效应。类比冲量,考虑资源在工序上的投入时间,能反映资源对该工序的推动情况。资源“冲量”计算式为

其中,Ir(i,k)表示资源k对工序i产生的“冲量”大小;r(i,k)、tr(i,k)分别表示资源k投入工序i的数量和持续时间。
本文对工序的资源紧张性由该工序使用的资源“冲量”占资源总量与总工期乘积的比例决定,不仅考虑资源使用数量与资源总量的关系,还将资源使用时间计算在内。当工序使用的资源数量越多,使用时间越长时,工序的资源“冲量”随之越大。当某一项工序的资源“冲量”越接近总资源数量与工期的乘积时,该工序资源紧张度越高,因此发生延期的风险就越大。假设项目用到的资源类型有m种,每个工序使用其中的若干种,工序i的资源紧张度为

其中,αi表示工序i的资源紧张度;R(k)表示资源k的总量;T表示项目估计工期。
2) 搭接网络复杂度。
链路网络复杂情况是度量项目缓冲区时不可忽视的关键部分。网络复杂度越高,项目完工的不确定性越高,因此用来吸收不确定性所需的缓冲尺寸越大。目前的研究一般假设项目网络为“结束-开始”衔接网络,从工序个数和工序持续时间两个方面计算网络复杂度,忽略了有多种逻辑关系的搭接网络的情况。
搭接网络中,由于不同逻辑关系的存在,工序之间首尾不相连,出现相互重叠或有时间间隔的现象。特别是当工序间存在相互重叠的部分时,项目管理者必须同时对两个工序的并行部分进行管理,加大了管理难度。因此,将工序的搭接率列为网络复杂度的度量因素之一是必要的,其计算式为

其中,Oi表示工序i的搭接率;ti-1,i表示相邻工序i-1和i同时进行的时间(并行时间) ;ti表示工序i的持续时间。
同时考虑紧前工序持续时间和工序搭接率,搭接网络复杂度为

其中,βi表示工序i的搭接网络复杂度;Np表示关键链上工序的紧前工序数目;表示工序i相应的紧前各项工序持续时间总和;表示工序i与紧前工序i-1的首尾间隔时间;Ti表示关键链活动总工期。
3) 相邻工序联系度。
以往的研究常常假设工序之间相互独立,而在实际情况中工序之间总是通过逻辑关系的存在而相互影响。本文按照工序间逻辑关系的不同,分情况计算相邻工序联系度。由于各种不确定性因素的存在,项目中的各个工序可能出现延迟或提前现象。为了尽量减少项目进程中可能出现的工期延迟传递与资源闲置浪费现象,应该适当增大缓冲尺寸。
在FTS和FTF关系中,紧前工序的结束时间分别影响紧后工序的开始与结束。而在STS和STF关系中,影响紧后工序的开始与结束的是紧前工序的开始时间。因此,本文分ST_ 和FT_ 两种情况进行分析。
在ST_ 情况下,相邻工序间可能产生延迟传递。紧前工序提前完工,会产生资源闲置浪费。以STS关系为例,工序i-1与工序i为关键链上的相邻工序,工序i-1开始后至少经过STSi-1,i时间,工序i才能开始。假设工序i按计划开始,受不确定因素的影响工期延长,分析工序i-1的延迟对i的影响。
当紧前工序i-1完成后续工序i必要的开始条件,且工序i-1不占用工序i的工作空间、人力资源和材料等资源时,它将释放足够的资源让下一个任务提前开始,同时继续推进自己的进程。工序i-1比工序i先开始且先结束,说明工序i-1的进度始终领先于工序i,此时工序间存在重叠关系。此处决定任务进程的是资源的分配策略,即项目工序受到组织逻辑关系的约束。
当工序i-1由于工期延迟占用工序i的资源时,应当考虑工序i所需资源的柔性程度,本文利用资源-技能矩阵(MRS) 来描述项目中所需资源的柔性程度。以人力资源为例,某项目需求的人力资源技能数量有m种,提供的专业人员数量为n,人力资源的资源-技能矩阵[18]为

假设工序i-1按计划开始,受不确定因素的影响使得工期缩短,分析工序i-1的提前完工对i的影响。在STS与STF这两种逻辑关系中,工序i受到紧前工序i-1的开始时间的约束,由于工序i-1的开始时间不变,因此无论工序i的开工柔性如何,都不会因为紧前工序提前完工而改变其开工时间。所以,在ST_情况下,相邻工序联系度λ 由紧后工序的资源柔性程度ρ 来决定,与紧后工序的开工柔性程度无关。
在FT_ 情况下,相邻工序间一定会产生延迟传递。紧前工序提前完工,可能会产生资源闲置浪费。以FTS关系为例,紧前工序的结束时间影响紧后工序的开始时间,因此,当工序i-1发生延期,工序i的开始时间将会延迟。
当紧前工序i-1提前完工时,如果工序i的开工柔性大,那么工序i可以在紧前工序结束后经过FTSi-1,i即可开工;否则,工序i需要等到原计划开工时间才能开始,紧前工序提前完工时间不能为项目周期所利用。因此,在此类关系约束中,紧后工序的开工柔性可以体现相邻工序之间的联系程度。本文引用模糊方法模糊集合 δi(θi)[19]确定开工柔性指数δ,度量工序的开工柔性大小。
0≤θi<a时,表示开工柔性很大,工序可以在紧前工序提前完工的情况下提前执行,此时的开工柔韧性 δi=0。a≤θi<b时,表示开工柔性适中,工序可以在一定程度上利用紧前工序提前完工节约的时间,此时的开工柔韧性 δi=0.5。b≤θi<1时,表示开工柔性很小,只能按照计划时间开工,不能利用紧前工序提前完工的时间,此时的开工柔韧性 δi=1。因此,可知隶属度函数 δi是θi的分段函数,函数表达式与示意图如式(9) 和图6所示。


图6 开工柔韧性隶属度函数示意图Figure 6 Membership function diagram of starting flexibility
其中,a和b的取值由项目所处的环境和项目经理等专家团队的经验、性格等主观因素决定。当以上因素对项目的总体影响倾向于项目的完成方向或有利于项目顺利完成时,参数a和b的取值偏大;反之,就会偏小。
综上,在ST_ 情况下,相邻工序联系度λi=θi;在FT_ 情况下,相邻工序联系度λi=δi。
1.4 项目缓冲确定模型
根据中心极限定理,将关键链工序安全时间集中在项目尾部,形成项目缓冲。缓冲聚合原理如图7所示,用xi表示工序i在50%完工保证率下的估计工期,yi表示工序i的安全时间,Y表示关键链上的项目缓冲。

图7 缓冲聚合原理Figure 7 Buffer polymerization principle
假设各活动的工期是相互独立的,图7中的(1)和(2) 两种情况下完成项目的不确定性程度不同,分别用链路的方差来表示,如式(10)、(11)所示。


如式(12) 所示,当所有工序的安全时间都集中在项目的末端,此时的缓冲量小于工序缓冲量之和,但提供了同等水平的保证。这意味着在项目结束时集中缓冲的做法不仅没有增加项目风险,还缩短了项目的总工期。
综上,基于工序逻辑关系的关键链缓冲确定模型为
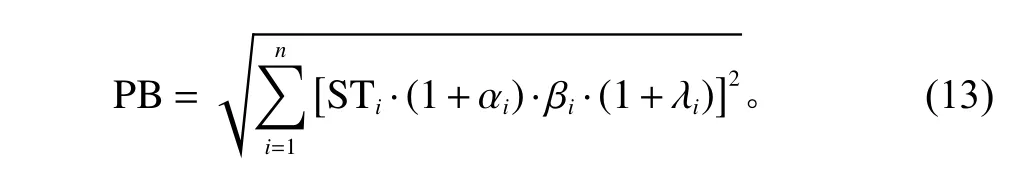
其中,n表示关键链上的工序数量;STi表示工序i的安全时间;αi表示改进后的资源紧张度;βi表示搭接网络复杂度;λi表示相邻工序联系度。
2 案例验证
为了说明本文所提出的项目缓冲确定模型的有效性,本文结合一个实际案例来对此方法进行验证。同时,为了排除外界干扰因素对仿真模拟的影响,保证实验的顺利进行,在案例模拟中提出如下假设。
1) 在项目执行过程中,受限资源的供应总量保持不变;
2) 项目中所有活动一旦开始进行,则必须到执行完成才能开始下一项活动,不可被其他活动中断。
2.1 案例描述
本文以一个软件开发项目为例。该项目从组织团队开始,到软件后期调试结束,共有14道工序,本文已知此项目的关键链表示为A→C→E→F→G→I→K→M→N。项目各工序的基本信息如表1所示,其中,编号里带有“*”的工序为非关键链工序,逻辑关系中“—”表示从结束到开始的衔接关系。所选取项目的网络示意图如图8所示,关键链已用虚线标出。

图8 项目网络图Figure 8 Project network diagram

表1 项目各工序信息Table 1 Information about the activities of the project
2.2 实验模拟
借助Matlab软件对本文提出的缓冲确定方法进行Monte Carlo案例仿真,由此产生1 000次模拟结果。
实验模拟将按照如下步骤进行。
1) 基于对数正态分布生成随机工期。
在Fallah等[20]看来,项目活动工期属于服从于对数正态分布的随机变量。如果Y~N(µ,σ2),则认为X=eY服从对数正态分布,即lnX~N(µ,σ2)。在项目的执行模拟过程中,本文假设σ=ST/2,对于每组µ和σ2,利用Matlab中的对数正态分布随机矩阵函数Ti=lognrnd(mu,sigma),产生1 000次随机工期。
2) 计算安全时间和缓冲影响因素。
由式(1) 和式(2),确定项目中各项工序的安全时间和工序间时距中的安全时间。计算关键链上工序的各项缓冲影响因素,结果如表2所示。

表2 关键工序缓冲影响因素计算Table 2 Calculation of critical activities buffer influence factors
3) 模拟缓冲确定模型。
根据项目的期望和方差,结合以上工序信息的计算结果,在Matlab中模拟本文建立的缓冲确定模型。仿真模拟围绕项目缓冲、实际工期、成本、时间累计概率和时间成本展开,针对不同指标产生仿真结果。
2.3 仿真结果分析
对本文方法和CPM、RSEM法进行实验模拟,比较项目缓冲、工期以及成本等模拟结果,得到的对比结果如表3、图9~ 图11所示。

图11 实际工期和成本对比Figure 11 Actual project duration and cost comparison

表3 本文方法同C&PM和RSEM对比结果Table 3 Results of the proposed method,C&PM and RSEM
根据表3、图9~ 11,可得出以下结论。

图9 3种方法缓冲大小对比图Figure 9 Buffer size contrast of three methods
1) 由表3和图9可知,本文方法所确定的缓冲为42.71 d,小于剪切粘贴法的56.05 d,大于根方差法的37.98 d;这是因为CPM方法采用“对半切”的方法来确定缓冲区,无论涉及多少个工序,都会导致缓冲区随着任务数量和持续时间的增加而线性增加,从而对项目造成过度保护。RSEM法假设项目工序之间相互独立,在中心极限定理的基础上用根方差量确定缓冲,因此导致项目缓冲比较小,模拟结果本文方法波动也比另外两种方法更平缓。此外,RSEM还采用“对半切”的方法来确定预留时间,没有考虑每一项工序各自的特点,因此可能造成不同的问题,如部分工序提取缓冲量大导致工期浪费,而部分工序提取缓冲量太小使之难以完工。不同于传统方法对所有工序都实行统一处理,本文在PERT中的三时估计法基础上确定各项工序的安全时间,所提安全时间更加符合项目实际情况,并基于项目工序间的逻辑关系对缓冲进行调整,因此所确定的缓冲尺寸更加合理。
2) 由表3可知本文方法实际工期为109.26 d,时间累积概率如图10所示,累计概率曲线斜率先增大后减小,项目工期呈正态分布,落在109 d的概率最大,与图11(a) 显示的仿真所得出的实际工期结果相符。

图10 本实验方法时间累计概率图Figure 10 Time-cumulative probability of the proposed method
3) 根据表3和图11显示,本文方法的实际工期是109.26 d,RSEM的实际工期是120.08 d,前者较后者工期相对缩短9.01%;RSEM实际成本356.347千元,本文方法实际成本337.892千元,成本相比减少5.18%。RSEM假设活动之间相互独立,导致安全时间抽取不足,由此活动预留时间增加,此时会由于学生综合症和帕金森定律等因素造成浪费,甚至存在超期完工的可能性。本文方法在安全时间抽取适当的情况下缩短了项目总工期,因此实际工期小于RSEM确定的实际工期。在项目总成本方面,由于本文方法在建立缓冲确定模型时没有过多关注成本指标,因此在项目实际成本的对比中,本文方法略低于经典方法,两者在成本方面的差距小于在项目工期方面的差距。
3 小结
本文提出基于项目工序间逻辑关系来设置关键链项目缓冲,对项目中大量不合理的安全时间进行提取,并结合项目的其他属性确定合理的缓冲尺寸,减少了学生综合征和帕金森定律等人为的因素带来的工期浪费。实验结果表明,本文方法在一定程度上缩减了项目完工所需要耗费的时间,节约了项目的总成本支出,提供了一种较为实用的项目管理新方法。
本文的局限性主要体现在仿真部分只模拟了成本与工期,对项目的其他指标如质量指标考虑不到位;另外,本文未考虑项目的资源缓冲。下一步将项目质量因素进行定量化研究,同时,具体分析不同资源特性,设置相应的资源缓冲。
