基于遗传算法的服装大规模定制生产线平衡优化
2023-01-06李雪飞
陈 莎,修 毅,李雪飞
(北京服装学院 信息中心,北京 100029)
在服装制造业中,互联网技术的应用有效促进了产销端信息平衡,催生出以需求驱动生产的大规模定制生产模式。与传统服装企业相比,服装大规模定制企业的生产订单具有单量小、款式多变、下单时间不确定等新特点,这就要求生产线要更具生产柔性[1]。若企业仍按标准生产线进行生产,势必会引起工位忙闲不均、生产设备利用率低等问题。另外,某些定制项复杂的订单根本无法在标准生产线上完成生产,因此大规模定制生产线平衡问题亟待解决。
在生产车间调度平衡优化的相关研究中,遗传算法(genetic algorithm, GA)及其改进算法的应用已相对成熟。基于GA的车间调度平衡研究主要分为2类:一是对车间调度数学模型不断改进使算法优化结果更切合实际生产需求。当生产方式由标准化大批量生产向多品种小批量生产转变,数学模型也相应转变为多品种混合生产车间调度问题模型。比如:考虑工件序列约束、以最小化最大完工时间为目标,构建动态流水车间制造单元调度问题模型[2];考虑加工质量、最大完工时间和加权成本等优化目标,构建多目标柔性作业车间调度问题模型[3];考虑工件到达时间、加工时间、排队规则出错等影响因素,构建不确定因素扰动的柔性作业车间鲁棒调度问题模型等[4],以上模型呈现出动态性、多目标性、不确定性及约束性等复杂的特性。二是对算法本身的改进以保证寻优效率和结果准确性。虽然GA有隐性并行性和全局解空间搜索能力,善于解决诸如车间调度这种规模大且复杂的非线性问题,但在实际应用时也会出现早熟收敛或收敛缓慢等不足,因此学者们会在基因编码、算法设计以及遗传操作等方面对标准GA进行改进,增加收敛速度。比如,在基因编码方面,采用自然数编码、三元组编码等多种编码方式,扩大了GA的使用领域[5-6];在算法设计方面,将模拟退火、拓扑方法、差异度阈值策略等理论思想嵌入GA框架中,有效提高了可行解的搜索能力[7-9];在遗传操作方面,对交叉、变异及适应度函数等进行自适应改善探究,使其可随迭代次数进行动态调整,避免迭代过程中的早熟收敛[6,10]等。
在服装领域,关于GA在大规模定制混合生产线平衡优化方面的应用探究还较少。目前大都是探讨单品种、工序数少的服装在标准生产线上的平衡优化,且以裤装、衬衫等工艺较为简单的服装品类为例进行算法验证[11-12],对于总工序数较多、包含多组子生产线、工艺更为复杂的西服品类混合车间调度平衡相关问题无法解决。本文基于GA相关理论,综合考虑工序约束、多优化目标、多子生产线以及混合投产等更为复杂的生产特点,对服装混合车间调度平衡问题进行探究,完成混合生产线平衡优化模型构建及满足约束的多目标优化算法设计,采用MatLab软件技术,结合实例进行可行性验证,有效提高服装大规模定制生产车间的工序编制效率,使智能优化算法在服装制造领域得到进一步的推广和使用。
1 生产线平衡模型构建
多品种服装共线定制生产的前提是,同一生产线上生产的通常都是结构、工艺相似,仅规格、部分部件不同的同品类服装。在该服装定制生产线中,个别定制工序存在的差别较大,其公共工序的工艺、工时是完全相同或仅略有差别,因此服装定制生产适合于构建混流生产平衡模型,其模型构建如下。
1)确定混合生产线。在某特定生产计划期内,根据单批次订单内服装产品的工序约束关系将各订单的服装工艺生产线整合为混合生产线。
以图1为例,假设有A、B、C 3个服装产品订单共线生产,工序约束关系及工时数据分别如图1(a)、(b)、(c)所示,依据公共工序合并,定制工序均保留的原则对所有种类服装工序进行整合,合并为图1(d)所示符合工序约束关系的混合产线。
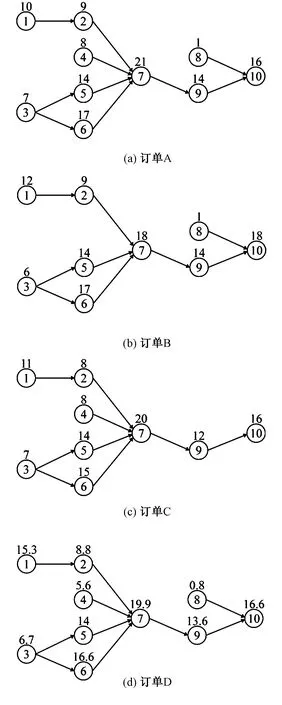
注:圈内数字为工序编号;圈外数字为工序对应的工时,单位为min。
2)确定综合工时。假设订单A、B、C的生产量分别为5、3、2,工时数据如图1(a)、(b)、(c)所示,根据式(1)可求出整合后混合生产线的各工序综合工时,最终形成如图1(d)所示的综合工序图。
(1)
式中:i为产品工序编号;Ti为工序i的综合工时;m为该生产单元内第m个服装定制订单(m=1,2,…,M);M为该生产单元内服装定制订单总数;qm为该生产单元内第m个服装定制订单的生产量;Q为该生产计划期内每个生产单元的投产量;tmi为第m个定制订单内服装产品的第i个生产工序的工时(当订单m内定制服装产品的第i个工序为空时,tmi为0 min)。
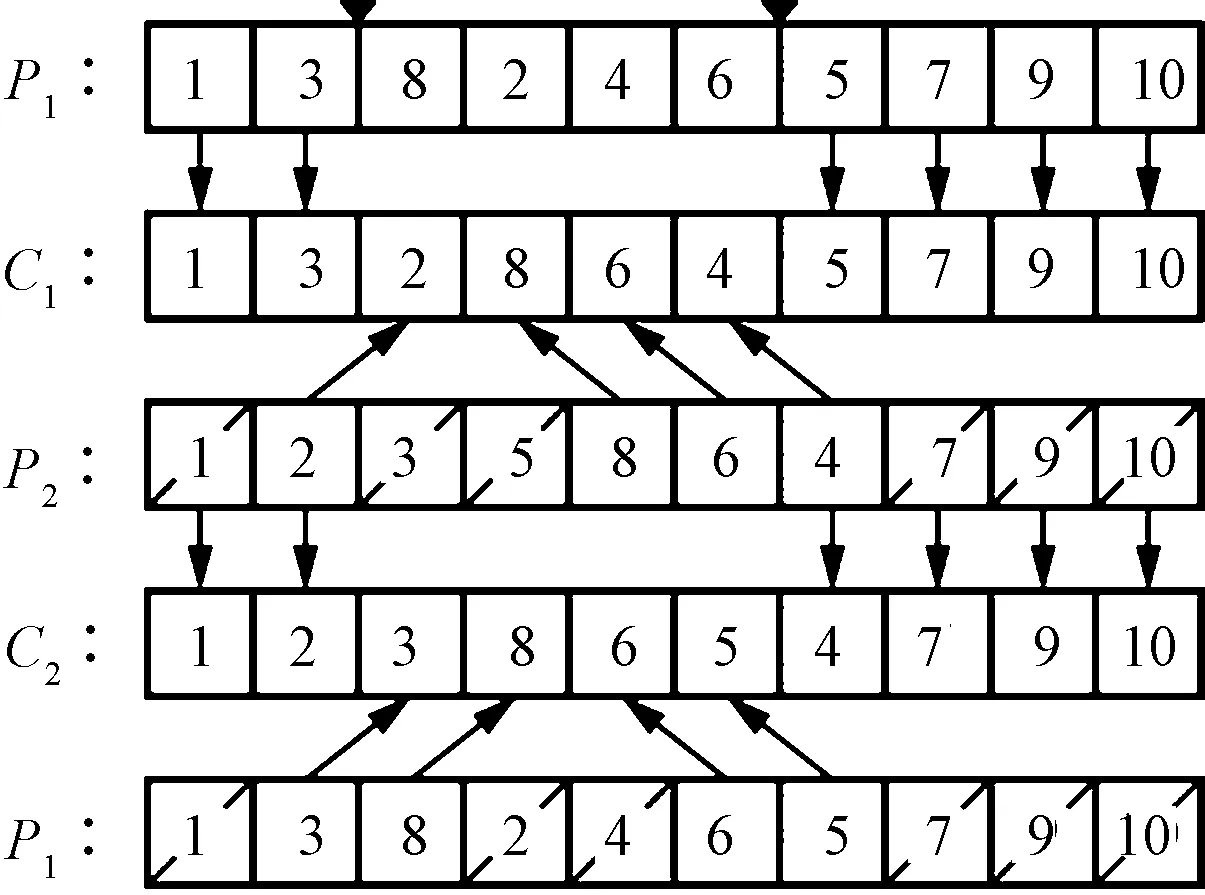
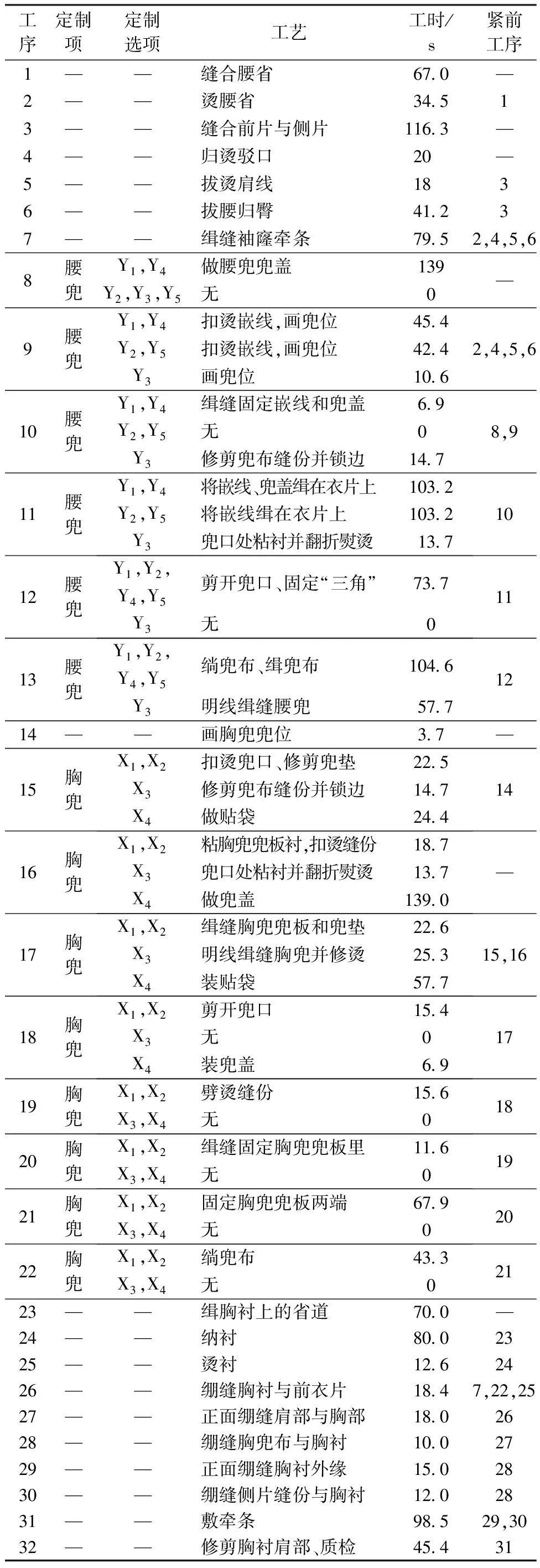
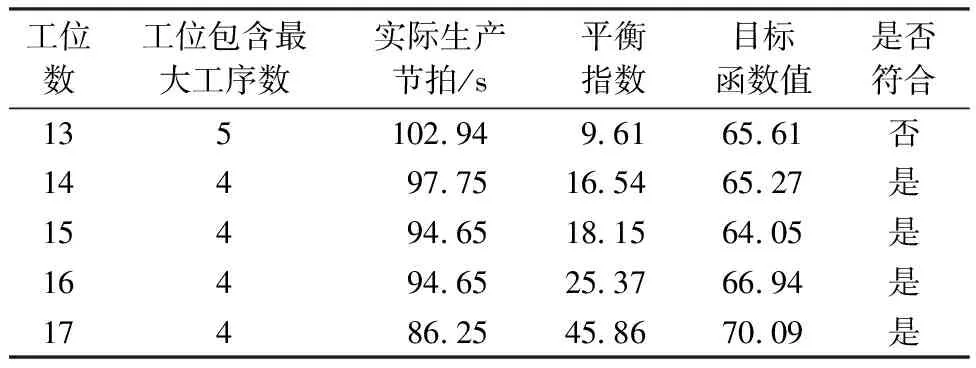
其中,生产单元内订单数M和订单内服装生产量qm的不同状态可衍生出各种生产模式。比如:当该生产单元包含订单数M=Q,qm均为1,即为个性化定制;M 3)确定优化方案。根据图1(d)所确定的生产线满足共线服装的工序约束及工艺要求,符合混合生产基本条件。 基于GA相关理论进行编码、解码及算法设计,完成工序编制方案的寻优操作。并根据式(2),求出该计划期内服装工序编制效率,对寻优结果进行验证,判断是否符合生产线编制效率一般大于85%的生产要求[13]。 (2) 由于GA通常不直接作用于问题解空间,所以需要通过编码设计将生产线平衡问题的可行解空间与GA的码空间相对应,合理的编码机制对算法质量和寻优效率有很大影响。本文主要以矩阵形式对工序、工时、综合约束关系3个部分进行编码设计:工序部分采用自然数编码如式(3)。每行代表1种符合约束关系的工序编制顺序,即1个可行解,s代表第s个可行解(s=1,2,…,S);S为工序编码矩阵中可行解总数;xsr代表第s个可行解的第r个生产顺序的工序号;工时部分采用实数编码,见式(4)每行数值代表1种服装的工时数据,tmi代表订单m内服装产品的第i个工序的具体工时;综合约束关系部分采用二进制编码,见式(5)。根据式(6)将所有工序按紧前约束关系生成N阶方阵A,aij代表工序i对工序j的约束关系。 (3) (4) (5) (6) 式中:i为该生产期内服装产品的工序编号(i=1,2,…,N);紧前工序为紧接某项工序的先行工序。 本文的解码过程不仅是将编码矩阵直译为符合约束关系的工序顺序,还需进一步按工序顺序将服装工序分配到工位,得到具体工序编制方案。 根据GA的码空间与问题的可行解空间的对应关系,种群由S条染色体组成,每条染色体对应一个可行解编码。以1条可行染色体为例,具体实现步骤如下。 (7) 步骤2:在满足式(8)的情况下,按基因编码对应的服装工序依次分配到前(K-1)个工位,剩余的服装工序无论总工时是否大于C,都分配到最后一个工位K上。 Tk≤C,(k=1,2,…,K) (8) 步骤3:判断工序分配是否结束。若此时仍满足Tk≤C,则工序分配结束,该染色体对应工序编制方案的实际节拍为C;否则,进入步骤4。 步骤4:计算各工位时间的潜在最小时间增量Δt1,Δt2,…,Δtk,…,Δt(K-1),其中,Δtk为分配至第(k+1)个工位第1个工序的工时。 步骤5:判断搜索是否停止。令工位实际节拍C=max{Tk|k=1,2,…,K},工位潜在节拍C′=min{Tk+Δtk|k=1,2,…,(K-1)}。若C≤C′,说明改变服装工序分配方案并不能使实际生产节拍更小,搜索停止,该分配方案即为此染色体个体的最优分配方案,实际节拍为C;否则,更新C值,以C=C′为新的实际生产节拍,转向步骤2重新对该染色体个体进行工序分配。 步骤6:步骤1~步骤5为1条可行染色体对应的解码过程。当种群数量为S时,需要将以上解码过程重复S次,生成S个问题可行解。 在满足服装工序约束的情况下,同时考虑工位平顺化和瓶颈节拍最小化2个优化目标,基于GA相关原理进行算法设计。基本框架如图2所示。 图2 GA基本框架 初始种群的设计在一定程度上影响后代染色体的质量与分布。在初始化过程中染色体个体既要随机分散地分布在可行解空间,也要满足工序约束;因此,采用符合工序约束的随机初始化策略来产生初始种群,使染色体都可译码为满足服装工序约束的随机可行解。具体实现步骤如下。 步骤1:令s=1,并根据服装综合工序图,得到综合工序约束矩阵A。 步骤2:根据约束矩阵A搜索无紧前工序或紧前工序已全部分配完毕的服装工序,即约束矩阵中对应列全为0,将其放入备选工序集合R。 步骤3:在集合R中随机选择一个工序,判断该工序编码是否已存在于第s个染色体的基因位中,若已存在,则重新随机选择;否则,分配给该工序1个染色体基因位,并更新约束矩阵A,即将矩阵A中已分配工序的行置0。 步骤4:再次转入步骤2更新备选集合R,当第s个染色体内基因总数与服装工序总数相同时,1条满足工序约束关系的可行染色体生成。 步骤5:更新s值,令s=s+1,重复步骤2~步骤4,直至生成S个染色体。 适应度函数是评价个体优劣的依据,函数设计既要能体现种群内个体差异,也要符合优化目标,另外适应度评价过程还要简洁高效,不然会一定程度影响GA的整体优化性能。本文平衡问题为多目标优化问题,优化目标主要有2个:一是整个计划期内总工作时间最小,表示为工位实际节拍C(瓶颈节拍)最小化(见式(9));二是各工位工作时间相对均衡,使产线运作更顺滑,表示为平衡指数F2最小化(见式(10))。本文结合企业生产实际,利用加权求和法将多目标转化为单目标,得目标函数F(见式(11))。 minC=min{maxTk} (9) (10) F=aC+bF2 (11) 式中,a、b为目标函数权值。 适应度函数f通常是目标函数F变换构成,个体适应度越高,基因越优,被遗传下来的概率也就越大。本文适应度函数为 (12) 3.3.1 选择操作 本文采用轮盘赌法对种群中染色体个体进行选择。具体实现步骤如下。 步骤1:制作轮盘。根据式(12)~(14)计算种群中所有染色体的个体适应度f(x)、选择概率px和累积概率wx。个体适应度越大,被选择的概率越大。 (13) 式中,x,s分别为种群中第x,s个染色体。 (14) 步骤2:转动轮盘。产生随机数r1∈(0,1]。 步骤3:确定轮盘赌结果。依次判断r1与wx的大小,当wx-1 步骤4:重复步骤2~步骤3,并保证迭代过程种群数量不变。 3.3.2 交叉操作 本文采用两点交叉法进行交叉操作设计。为通过交叉操作增加种群多样性的同时,保证交叉后的染色体序列仍满足服装综合工序约束,具体实现步骤如下。 步骤1:首先选取种群内第s、(s+1)个染色体作为一对父代染色体。 步骤2:产生随机数r2∈[0,1],并判断r2与交叉概率pc的大小。若r2 步骤3:交叉操作过程。随机生成2个交叉点,如图3所示。将父代P1除交叉片段以外的基因片段直接复制给子代C1,然后再将P1交叉片段基因编码在父代P2中搜索出来,并按P2中基因顺序赋给子代C1,一条符合工序约束的可行子代染色体便产生了。对于子代C2的产生过程同理。 图3 交叉操作 3.3.3 变异操作 本文在变异操作设计中,采用单点变异法。为保证变异后的染色体序列仍为满足服装综合工序约束的可行编码序列,具体实现步骤如下。 步骤1:产生随机数r3∈[0,1],并判断r3与变异概率pm的大小。若r3 步骤2:变异操作过程。如图4所示,随机产生变异点,变异点之前的染色体片段直接复制给子代,变异点后按照种群初始化的方法重新生成一段可行的染色体片段,一条新的子代染色体便产生了。 图4 变异操作 步骤3:以上变异操作重复S次。 3.3.4 精英保留 本文为保证每代几个较优解不被遗传操作所破坏,对迭代进化过程新增一步精英保留操作。精英保留策略会将每代种群中几个较优个体,即适应度最高的几个可行染色体序列,直接复制到下一代种群,同时为保证种群总体数量不变,将经遗传操作后产生的子代种群中适应度最差的相同数目个体删除。 本文以某西服大规模定制生产企业为例进行实例分析。该企业生产车间混合生产线包括前片、过面、后片、领子、袖子、组装共6组子生产线,保证物料在组内直线传送,无组间交叉,总工序数达103道,单批次投产量最大为25,则以25件服装产品为一个生产单元进行混合批量投产。 以前片子生产线为例,某生产单元内定制订单信息如表1所示。综合工艺信息如表2所示。将该实例中GA相关参数设置如下:目标函数权值分布为a=0.6、b=0.4,初始种群大小S=30,交叉概率Pc=0.8、变异概率Pm=0.3,迭代次数G=300。 表1 西服订单信息表 根据GA算法特点,当G取值过大时,会降低运行速度,过小则无法收敛。本文G值是由具体生产数据多次试运行确定的合理值,运行结果是经G次迭代后保存下来的最优结果。表2中腰兜共包含5个定制选项,具体为:Y1表示直兜带兜盖;Y2表示直兜双牙;Y3表示明贴兜;Y4表示斜兜带兜盖;Y5表示斜兜双牙;胸兜共包含4个定制选项,具体为:X1表示直型;X2表示船型;X3表示明贴兜;X4表示猎装口袋。 表2 西服综合工艺信息表(前片组) 由于各组子生产线工位数未知,在借助MatLab技术进行生产线平衡优化过程中,首先会基于“单工位包含工序数一般不大于4”这一编制原则确定前片组工位区间并进行试优化;然后结合人力成本、设备消耗成本等因素对表3中试优化结果进行综合比较,认为K1=14时前片组优化结果最好。 表3 试优化结果(前片组) 另外,在试优化过程中发现,有些工序会因其综合工时大于平均工位节拍影响到整体生产平衡,比如前片组工序3,本文会将其视为2个子工序(如表4中工序3-1、3-2),默认这样的工序可同时分配到2个工位,相应工时减半。对算法运行出的最优工序编制结果整理后,得前片组工序编制具体方案如表4所示。其他子生产线组同理。 表4 工序编制方案(前片组) 在保证各子生产线组内生产平衡的同时,还要考虑各生产线组之间平均工位节拍是否达到相对均衡。因此,在确定前片组平均节拍后,其他各组潜在工位数Ku分别由K′u进行四舍五入取整所得。 (15) 当Ku≤20时,子生产线u以工位区间[Ku-1,Ku+1]进行试优化,当Ku>20时,则以工位区间[Ku-2,Ku+2]进行试优化。 最终西服各组子生产线综合最优工序编制效率汇总如表5所示。总生产线工位数为56,平均编制效率为85.77%,符合生产线编制要求。 表5 工序编制效率汇总 本文对更为复杂的具有工序约束的混合生产线平衡调度问题进行了深入探究并构建全新模型,该模型不仅适用于服装大规模个性化定制,也适用于多品种小批量生产及单品种标准化生产,具有良好的兼容性。 本文完成了工位实际节拍最小化及平衡指数最小化多目标优化工作。同时,结合实际生产特点,建立了工序约束以保证染色体在迭代过程仍全部有效,提高了算法运算速度和较优解的搜索能力。 在服装大规模定制生产线上,服装种类和投产数量比例相对稳定为宜,服装投产比例或种类发生较大变化时,工位分配方案应随之做出相应调整。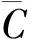
2 编码与解码设计
2.1 编码设计

2.2 解码设计
3 算法设计

3.1 种群初始设计
3.2 适应度函数设计
3.3 遗传操作设计

4 实例分析
4.1 遗传参数设置

4.2 结果分析

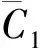
5 结束语
