基于用户时空活动与模糊决策的电动汽车充电需求预测
2023-01-05屈琦凯沈永俊
鲍 琼 谭 旭 屈琦凯 沈永俊
(东南大学交通学院,南京 211189)
随着社会经济与交通运输业的快速发展,以燃油车为主体的现代公路运输带来了日益突出的不可再生能源消耗、碳排放以及大气污染等环境问题,发展新能源汽车成为大势所趋[1-2].在国家政策扶持下,截至2021年底我国新能源汽车保有量已达784万辆,其中纯电动汽车占81.63%,其数量增长迅猛,发展前景广阔.可以预见,电动汽车的规模化应用将引发总量庞大的充电需求.然而,由于对电动汽车充电需求缺乏清晰了解,目前我国的充电设施建设在总体上仍存在较大缺口,而在局部普遍存在时间或空间上供需不匹配等问题,电动汽车用户停车充电难等问题屡见不鲜[3].因此,准确预测电动汽车用户的充电需求时空分布是科学规划充电设施的关键前提,对于进一步发展和推广电动汽车具有重要意义.
电动汽车充电需求受车辆电池、充电设施、充电价格等客观因素以及用户出行与充电行为心理等主观因素影响[4],具有较大随机性.近年来,国内外学者针对电动汽车充电需求的研究由时间分布预测发展到时空分布预测.田立亭等[5]基于美国家庭出行调查(NHTS)数据,考虑用户开始充电时刻、日行驶里程与充电功率等变量,结合蒙特卡洛方法预测了单辆与多辆电动汽车的充电功率需求.Moon等[6]根据消费者对电动汽车的偏好、充电时间和供电设备类型预测充电需求的变化,并提出了电动汽车基础设施建设的注意事项与政策建议.Pareschi等[7]对比分析了不同充电行为场景下的充电需求,并对电池容量、充电功率、运行能耗等模型参数进行了敏感性分析.
电动汽车充电需求的时空分布预测大多按行政区或用地类型进行空间划分.Knapen等[8]应用FEATHERS活动模型计算了比利时弗莱芒区居住区与工作区的电动汽车充电负荷.张洪财等[9]基于停车生成率模型预测了电动汽车充电需求时空分布,对深圳市多个行政区的居住区、工商业用地充电负荷曲线进行了计算分析.温剑锋等[10]、赵书强等[11]、Wang等[12]基于出行链理论深入挖掘了NHTS数据中的用户出行规律,通过蒙特卡洛方法模拟了住宅区、工作区、休息区、商业区等用地的电动汽车充电负荷.还有少数研究结合交通模型分析了道路网中路段或节点的充电需求分布.其中,李磊等[13]考虑了动态交通信息对电动汽车用户出行与充电行为的影响.Yang等[14]考虑了电动汽车用户出行选择的有限理性,描述了各活动链上电动汽车的时空转移规律和充电需求.然而上述研究普遍存在充电需求空间分布预测颗粒度较大的问题.
除此之外,现有研究大多假设电动汽车与燃油车出行特性相同,从而根据居民出行调查或燃油车运行数据估算充电需求,然而对用户充电行为考虑较为单一、缺乏数据支撑,譬如考虑用户在电量低于某一阈值时充电.实际上,用户对于电量高低的判断并非有统一、明确的标准,其充电决策也并非仅考虑电量因素.此时,模糊逻辑为用户充电决策建模提供了新方法,通过隶属度函数处理不确定性问题,能够模仿人脑思维方式进行推理和综合判断,对于模拟用户充电决策有较高的契合度[15].
综上所述,尽管现有研究关注不同的影响因素、从不同角度出发提出了多种电动汽车充电需求时间和空间分布的预测方法,但普遍存在对用户行为考虑不够完善,预测精细度不足的问题,并且局限于对影响因素的定性分析.本文基于电动汽车实际运行数据,构建用户出行-充电行为链,结合交通模型充分描述用户时空转移规律,并结合模糊逻辑刻画用户充电行为,应用蒙特卡洛方法对电动汽车用户群体的出行与充电行为进行模拟,以此建立电动汽车充电需求时空分布的精细化预测方法,并对其中关键影响因素的作用效果进行了定量化分析.
1 用户出行-充电行为链构建
出行链是个人为了完成日常活动按时间顺序先后到达不同目的地全过程的连接形式,包括时间链与空间链,包含出发时间、行程时间、停驻时间、目的地位置、行程距离等关键时空变量信息.本文以日常通勤者为研究对象,其出行链主要包括2种形式:① 从家出发到工作单位再返程,记为H-W-H链;② 从家出发到达工作单位,结束工作后前往休闲场所进行购物、娱乐等活动,最后回到家,记为H-W-C-H链.对于电动汽车用户而言,每次出行到达目的地后在停驻时间内存在潜在的充电机会,由用户对充电与否进行判断决策.用户出行行为与潜在充电机会在时空上构成了用户出行-充电行为链,如图1所示.
本文研究数据源自上海市新能源汽车公共数据采集与监测研究中心采集的50辆荣威E50纯电动汽车的使用数据,包括采集时间、累计行驶里程、荷电状态(SOC)、经度、纬度、启动时间、熄火时间、车辆状态等数据.该样本数据时间跨度为2015-06—2016-06,各车辆被记录的时长为3~12个月,最短记录时长为85 d,而最长为340 d,每车平均记录时长为214 d.最终从原始数据中识别提取出15 137次出行行程信息与8 498次充电行为信息,其中出行行程信息包括出发时间、行程时间、行程里程、行程速度、行程耗电量、停车时长等,充电行为信息包括充电开始时间、充电时长、充电前SOC、充电量、充电后SOC等.本文基于蒙特卡洛方法对用户出行的空间转移、路径选择、行程特征等相关时空变量以及用户充电决策进行随机概率建模与抽样,以模拟电动汽车用户群体的出行与充电行为.
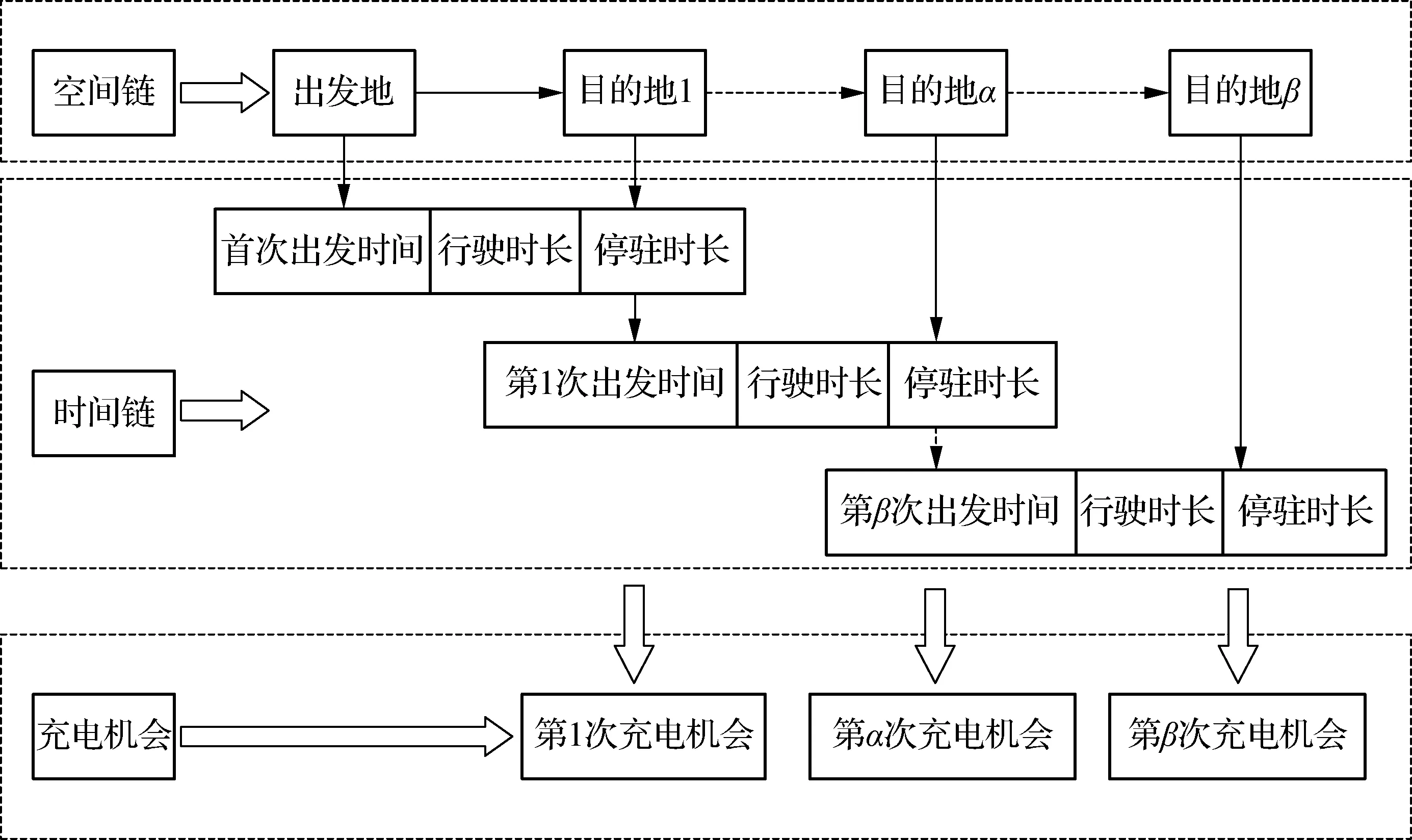
图1 用户出行-充电行为链示意图
1.1 出行行为建模
1.1.1 空间转移模型
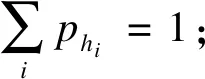
1.1.2 路径选择模型
预测模型考虑用户确定出发地与目的地后在城市道路网中的路径选择行为,类比多路径交通分配方法,假设用户的路径选择行为具有随机性,且其概率与满足用户出行目的的各条有效路径的长度有关.
有效路径是用户出发地与目的地之间由有效路段连接而成的路径,用户沿着有效路径行驶一定会距目的地越来越近.各条有效路径被用户选择的概率采用Logit型离散选择模型计算,如下式所示:
(1)
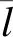
1.1.3 行程特征模型
在用户出行空间链基础上确定首次出行时间、行程速度、停车时长等行程特征量,即可得到用户出行时间链.在MATLAB中拟合行程特征的概率分布,对比正态分布、对数正态分布、指数分布、广义极值分布等连续随机变量分布模型,将loglikelihood值最大的作为最优分布,建立概率模型如下.
用户首次出行时间存在多峰特征,采用混合高斯分布(GMM)拟合,其概率密度函数如下式所示:
(2)
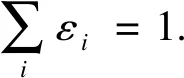
用户行程速度在低速区间较为集中,行程速度越高则频率越低.经比选,用户行程速度分布以广义极值分布拟合最佳,其概率密度函数如下式所示:
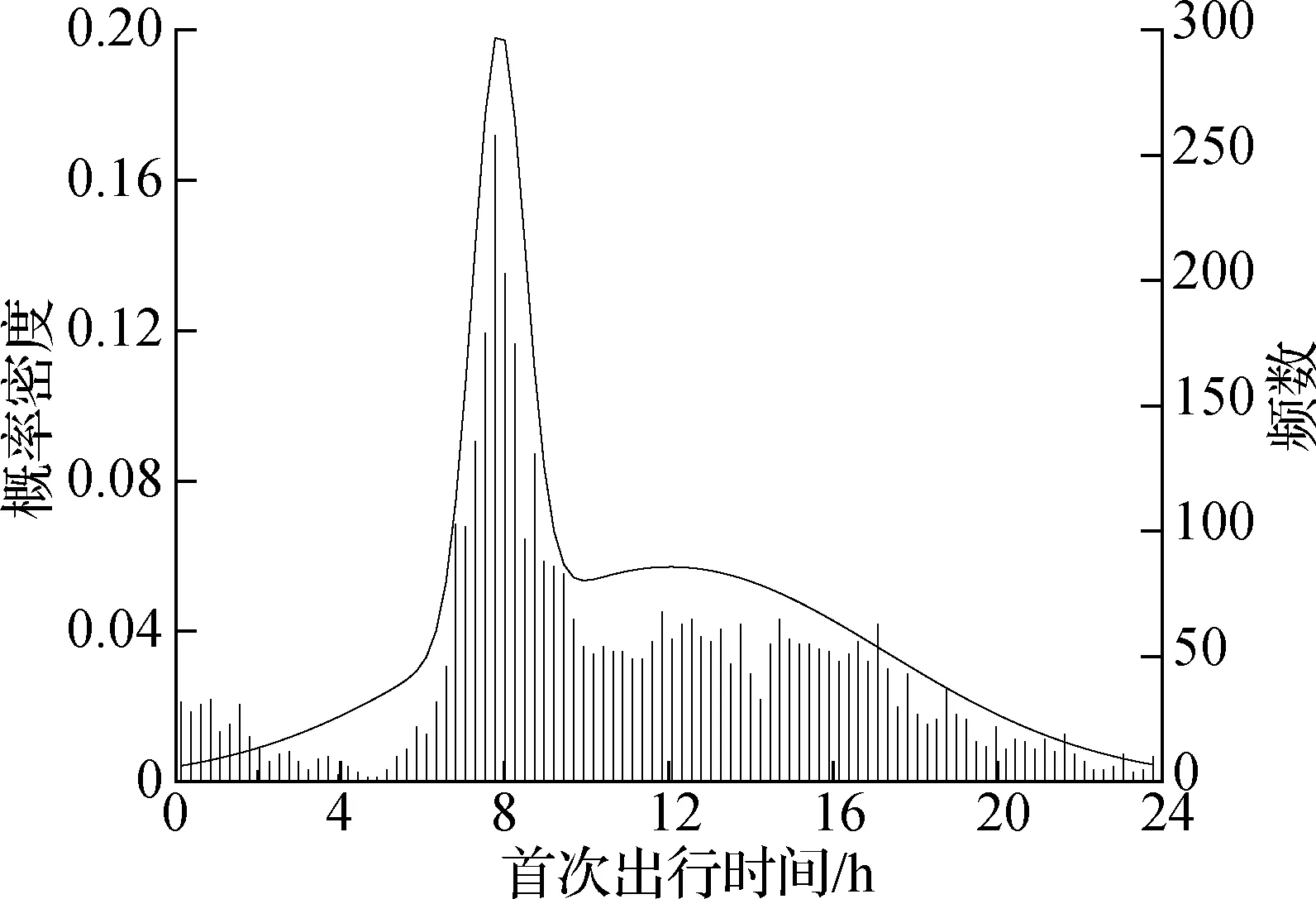
图2 用户首次出行时间概率分布拟合
(3)
式中,μ为位置参数;σ为尺度参数;λ为形状参数且λ≠0.拟合结果显示,μ=16.290,σ=5.882,λ=0.337.用户行程速度的频数分布与概率密度曲线拟合结果如图3所示.
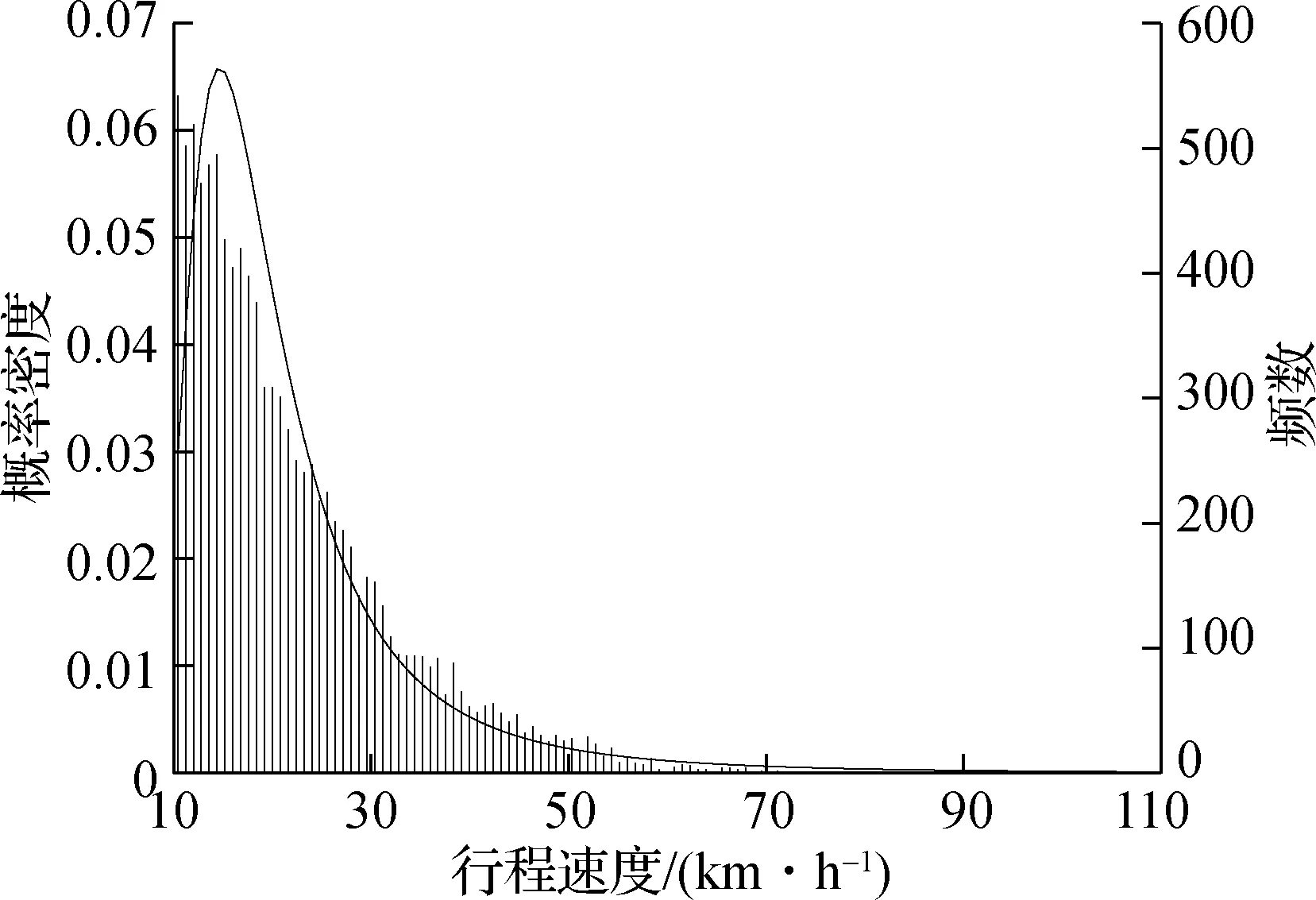
图3 用户行程速度概率分布拟合
用户停车时长的分布特征与行程速度分布特征相似.经比选,用户停车时长分布以对数正态分布拟合效果最佳,其概率密度函数如下式所示:
(4)
参数标定结果为μ=5.097,σ=1.568,用户停车时长的频数分布与概率密度曲线拟合结果如图4所示.
1.2 用电行为建模
1.2.1 运行耗电
电动汽车的出行能耗主要受行驶距离影响,假设耗电量与行驶里程成正比,建立电池荷电状态消耗与行驶里程关系如下式所示:
(5)
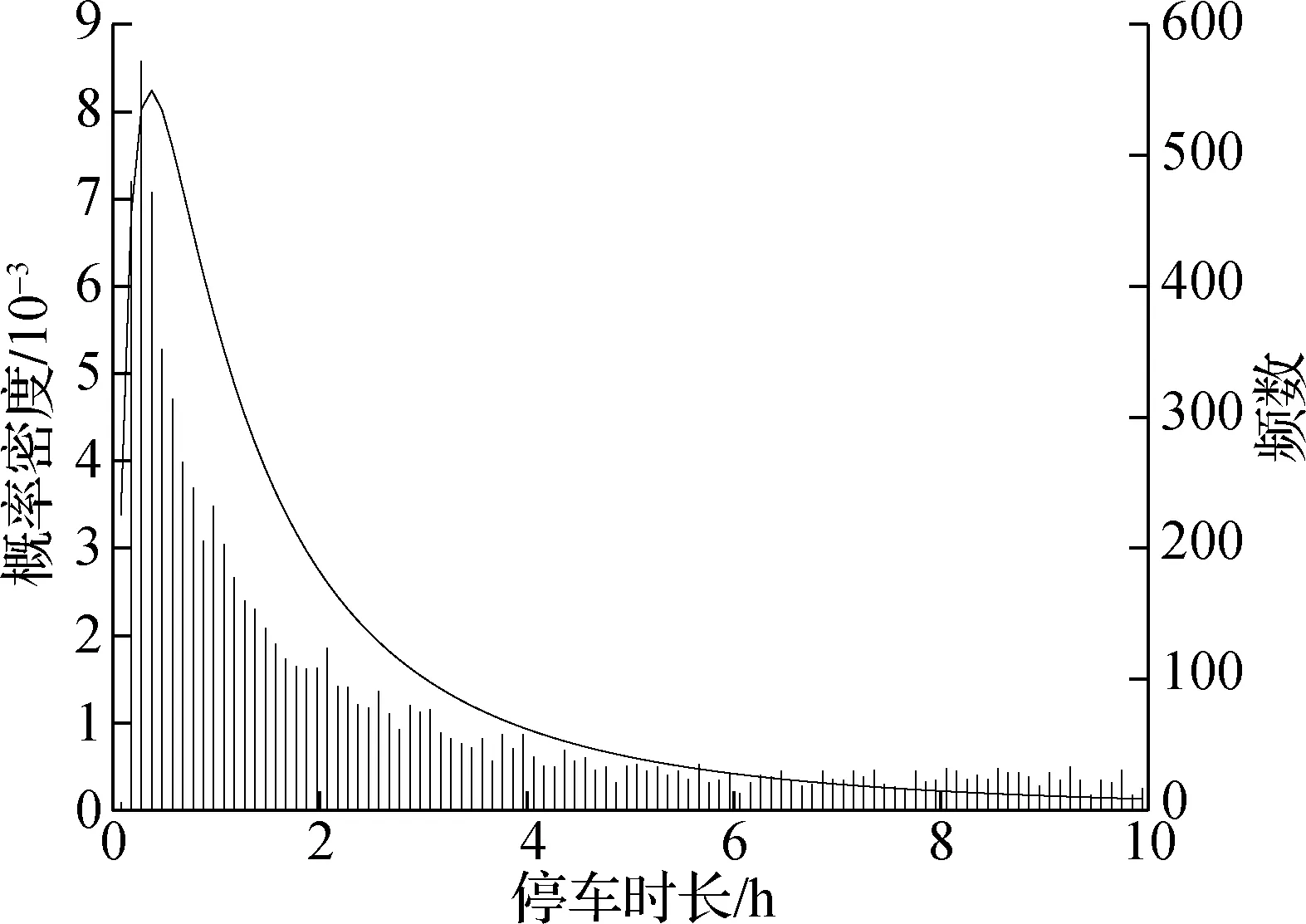
图4 用户停车时长概率分布拟合
式中,ΔS-为行程耗电量,%;l为行驶里程,km;E100为车辆每100 km耗电量,kW·h;C为电池容量,kW·h.其中,荣威E50车型的电池容量为22.4 kW·h,经线性拟合可得其每100 km耗电量为20.4 kW·h.
1.2.2 充电功率
根据用户每次充电的充电量与时长可推算其充电功率,如下式所示:
(6)
式中,P为充电功率,kW;ΔS+为充电量,%;T为充电时间,h.根据数据统计,用户充电功率主要集中在3.5~4.5 kW的区间内,平均充电功率为3.8 kW;为简化模型、减少计算量,设该值为用户充电实际功率.
1.2.3 充电决策
本文定义用户在当前电量不足以满足下次出行耗电时所必须进行的充电为刚性充电;反之,则为弹性充电.对于刚性充电,若用户在计划停车时长内无法满足充电需求,则延长停车时长并充电至能够完成下次出行为止;对于弹性充电,考虑用户在停车时长内的最大可充电量与充电价格等因素,建立模糊逻辑推理系统模拟用户充电决策,确定用户选择充电的概率.
停车时长内最大可充电量与停车时长、电池当前荷电状态有关,由下式表示:
(7)
式中,ΔSmax为停车时长内最大可充电量,%;Tpark为停车时长,h;S为当前荷电状态,%.
充电价格c(t)分为峰时电价与谷时电价.以上海市居民用电收费为参考,06:00—22:00电价为0.617元/(kW·h),其余时段价格为0.307元/(kW·h).
建立模糊逻辑推理系统的关键在于定义输入输出变量的模糊隶属度与推理规则.在用户弹性充电决策模糊推理系统中,ΔSmax与c(t)为输入变量,用户充电概率为输出变量.对ΔSmax定义较低、中等、较高等3个模糊集合作为用户对ΔSmax的判断,c(t)属于谷时电价cvalley或峰时电价cpeak,对充电概率定义低、较低、中等、较高、高等5个模糊集合反映用户充电概率.本文定义弹性充电决策系统中输入输出变量的模糊隶属度函数如图5所示.
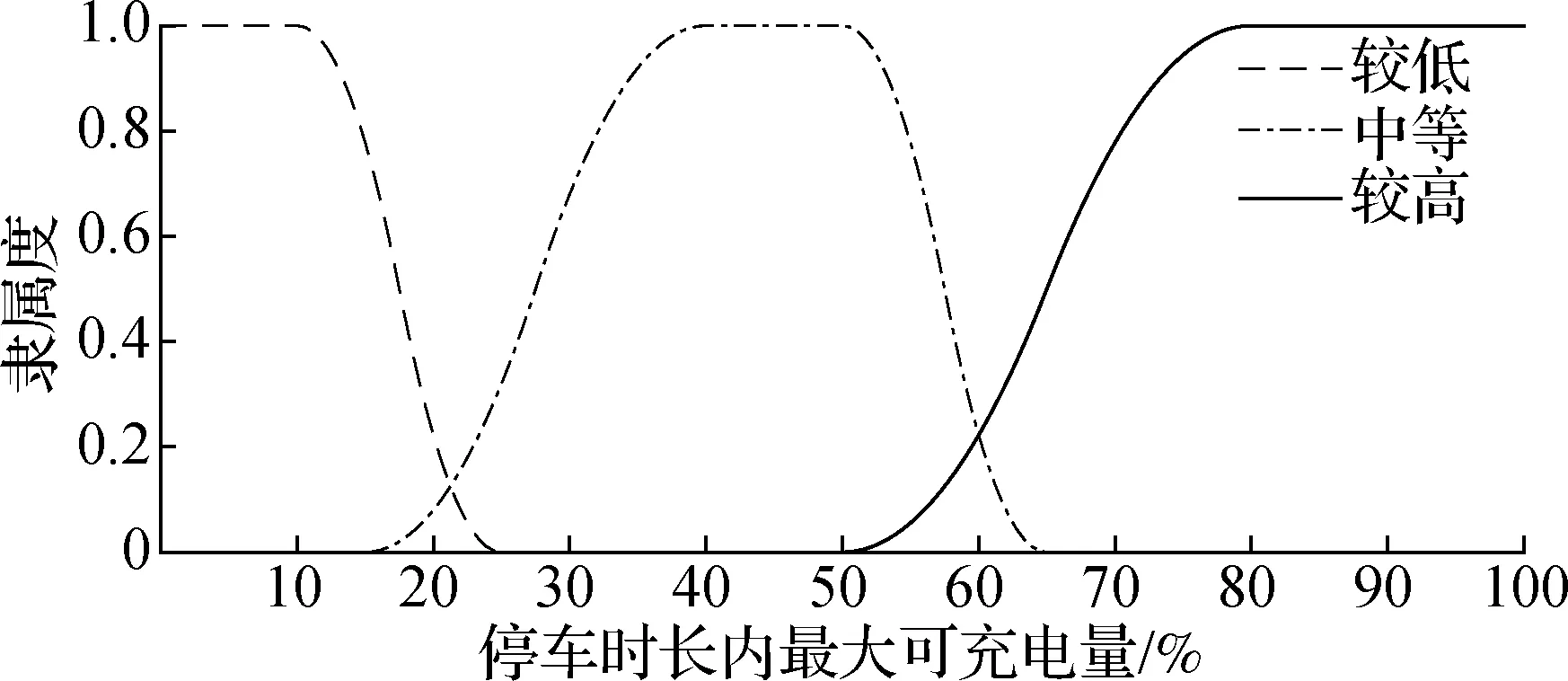
(a) 停车时长内可充电量模糊隶属度
结合用户实际充电行为特征,定义6条模糊推理规则,如表1所示.

表1 充电决策模糊推理规则
该系统运用取最小值方法进行“且”运算,通过求解质心对输出进行去模糊化,求得用户弹性充电的概率.
2 充电需求时空分布模拟计算方法
基于用户出行-充电行为链,采用蒙特卡洛方法模拟用户群体的出行与充电行为.对某一用户个体,首先应根据其出行链类别与空间转移特征在空间链上随机生成其居住区、工作区以及休闲区(若有)的空间位置,并对每一次出行的路径进行选择以确定行程距离;在时间链上,应根据用户行程特征首先抽取其首次出行出发时间,对于每次出行过程抽取行程速度以计算行程时间,并在其中途行程结束后抽取停车时长,每次行程与停车结束后及时更新当前时间.
时刻关注电动汽车电池荷电状态,并在用户每次耗电和充电行为发生后及时更新.假设所有用户每天从家出发时的电量服从80%~100%的均匀分布,用户行程途中每经过一个节点时根据当前电量是否支持行驶到下一邻近节点判断是否需要充电,若需要则充电至电量足以到达目的地或充满为止;用户每到达一个中途目的地时根据当前电量、停车时长与到下一目的地的距离进行充电决策,最后用户回到家中停车充电直至第2天同一首次出行时间出发.
若模拟过程中用户发生充电行为,记录其充电地点、充电量、充电功率与开始时间,并计算充电持续时长,最终对所有用户的充电功率在空间节点与24 h时间轴上进行叠加,得到电动汽车用户群体的充电需求时空分布特征.
3 算例分析
3.1 仿真场景与参数设置
以Nguyen-Dupuis路网[16]为仿真场景,该路网共有13个节点、19个路段,假设所有节点均有充电设施且所有路段双向均可通行,其拓扑结构如图6所示.其中节点1、4、5、12为居住区,节点2、3、8、13为工作区,节点6、7、9、10、11为休闲区,相邻节点间的距离如表2所示.
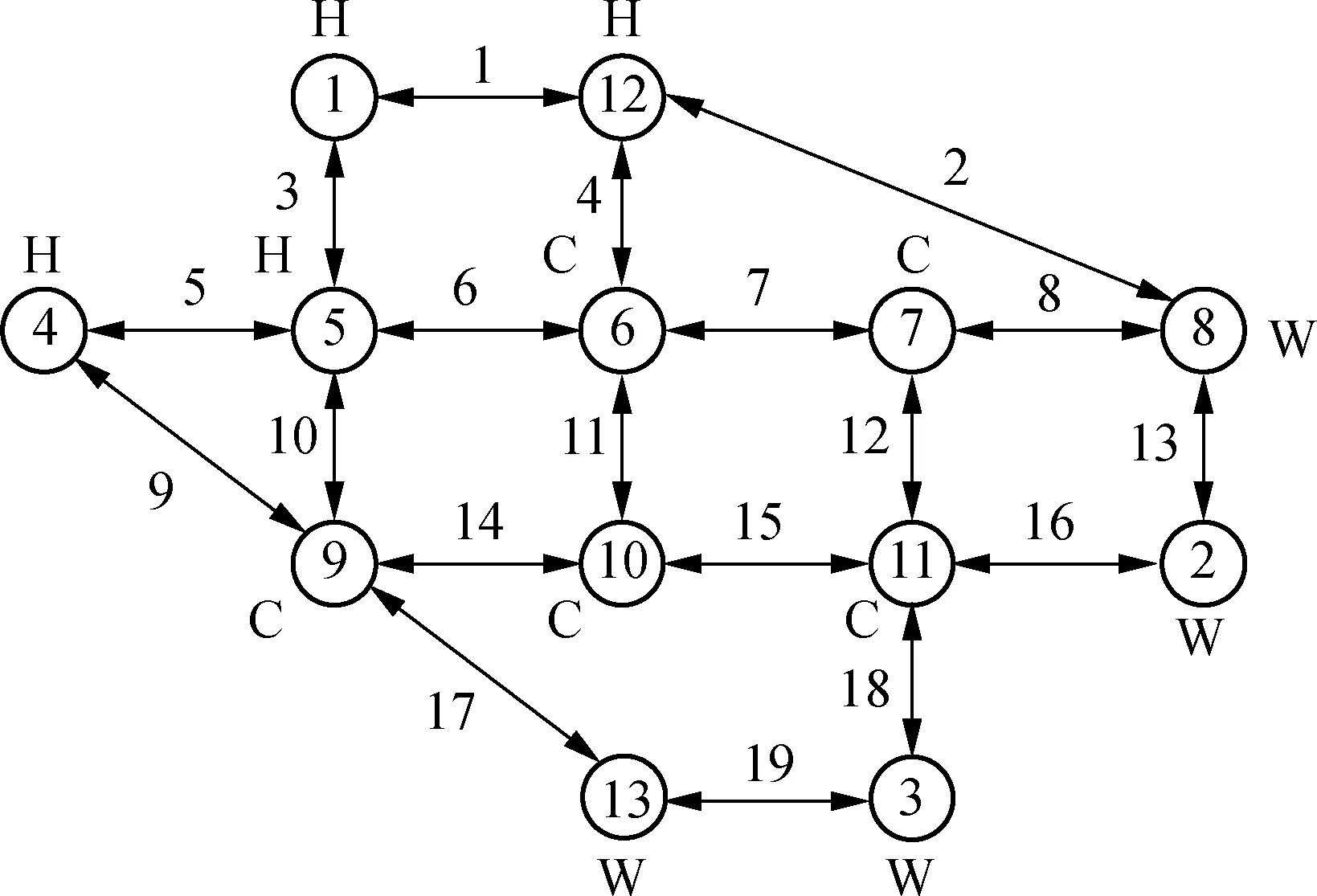
图6 Nguyen-Dupuis路网拓扑结构
设研究区域内某一工作日有2 000个用户出行,且H-W-H与H-W-C-H出行链各占50%;用户居住在节点1、4、5、12的比例为0.4∶0.3∶0.2∶0.1;用户由居住节点转移到工作节点,以及由工作节点转移到休闲节点的概率矩阵分别如表3和表4所示.基于上述环境条件对荣威E50用户的出行与充电行为进行模拟.
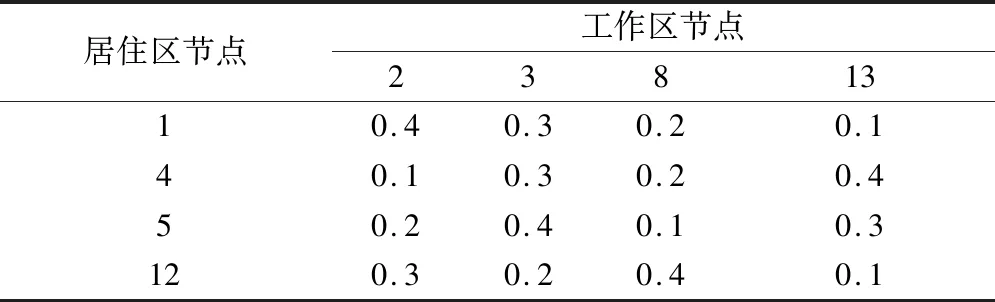
表3 用户由居住节点转移到工作节点的概率矩阵
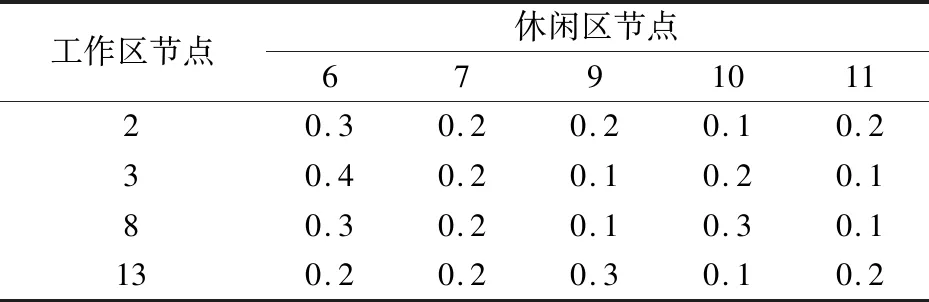
表4 用户由工作节点转移到休闲节点的概率矩阵
3.2 充电需求时空分布仿真预测结果
2 000个用户经过一个工作日的模拟运行,共产生3 673次充电需求,其中在行程途中发生充电15次,充电需求总量为42 511 kW·h.图7(a)显示,用户工作日充电功率存在2个峰值,在晚上21:00达到最高峰5 232.6 kW,于上午10:27到达次高峰4 316.8 kW,同一时刻最多有1 377辆车(占68.9%)在同时进行充电.
在空间分布上,不同用地类型的充电需求负荷曲线如图7(b)所示.居住区充电量占需求总量的59.8%,充电负荷从下午16:00左右开始逐渐累积,直至21:00达到最高峰4 993.2 kW,而后逐渐衰减并且于凌晨04:43归零,此时所有用户夜间充电完成.工作区是用户出行-充电行为链中首次充电机会的所在地,其充电需求量占比为35.7%,充电高峰时刻为上午10:27,峰值功率为4 316.8 kW,结合图7(a)可知,区域总负荷的次高峰完全由工作区充电需求产生;工作区充电由早上06:36持续至下午15:32.休闲区充电需求最少,占比为4.5%,其充电高峰时刻为18:50,对应负荷为623.2 kW.充电需求的预测结果符合用户使用电动汽车出行和充电的基本时空规律.
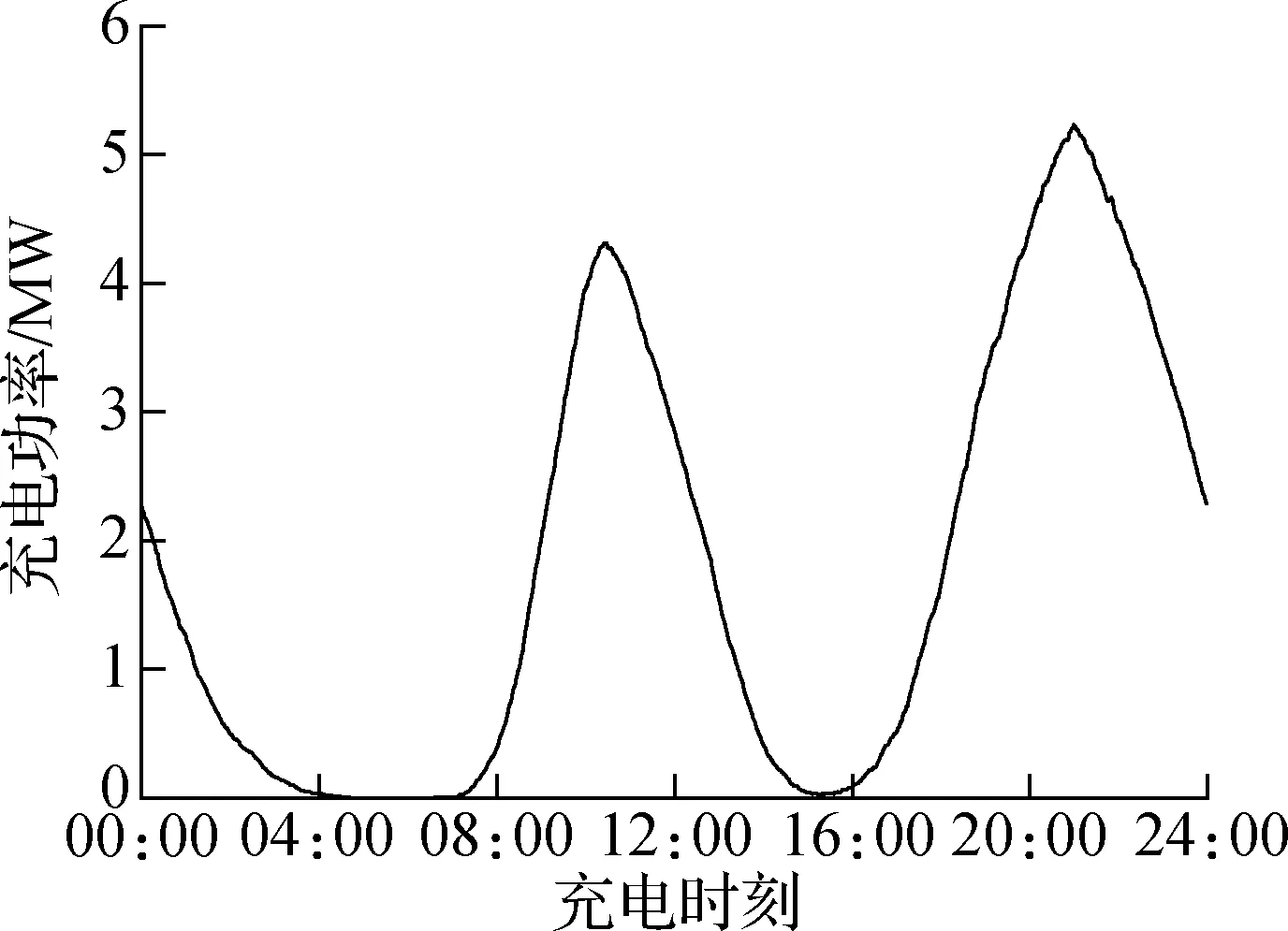
(a) 工作日区域充电需求总负荷曲线
各功能区电动汽车用电高峰时刻区域路网充电需求的空间分布如图8所示.受用户居住区分布不同影响,当居住区总体充电功率处于最高峰时,充电需求更多分布在节点1、4,节点5次之,节点12相对最少;受空间转移分布影响,当工作区充电负荷处于最高峰时,节点2、3承担的充电需求更多,节点8、13的用户充电需求相对较少;在休闲区充电高峰时刻,居住区节点仍有较多充电需求,休闲区节点充电负荷较少,工作区节点几乎不存在充电需求.
3.3 充电需求影响因素敏感性分析
现有研究主要从用电角度出发,考虑不同的价格引导方式、充电行为模式、充电设备条件下的充电需求变化,而普遍忽略了用户交通行为造成的影响.
本文综合考虑影响充电需求的交通因素与用电因素,通过对用户规模、出行链比例、用户首次出行时间、行程速度、停车时长、电池容量、百公里耗电与充电功率等充电需求预测变量在上述仿真条件基础上分别进行10%的上下浮动[7],研究用户在居住区与非居住区充电需求总量、峰值时刻、峰值功率等关键指标的变化,以进行影响因素的敏感性分析,结果如表5和表6所示.
当用户规模上下浮动10%时,充电需求总量与峰值功率在居住区均有超过10%幅度的变化,在非居住区变化幅度接近10%,而对于峰值时刻无影响.
用户出行链占比变化仅对各区域充电功率峰值有轻微影响,当H-W-H链比例提升10%时,峰值功率在居住区有轻微下降,而非居住区有微幅上升,这是由于用户总体出行次数减少,出行耗电与回家后充电相应减少;同时,由于中途充电机会减少,用户更倾向于把握在工作区仅有的充电机会.
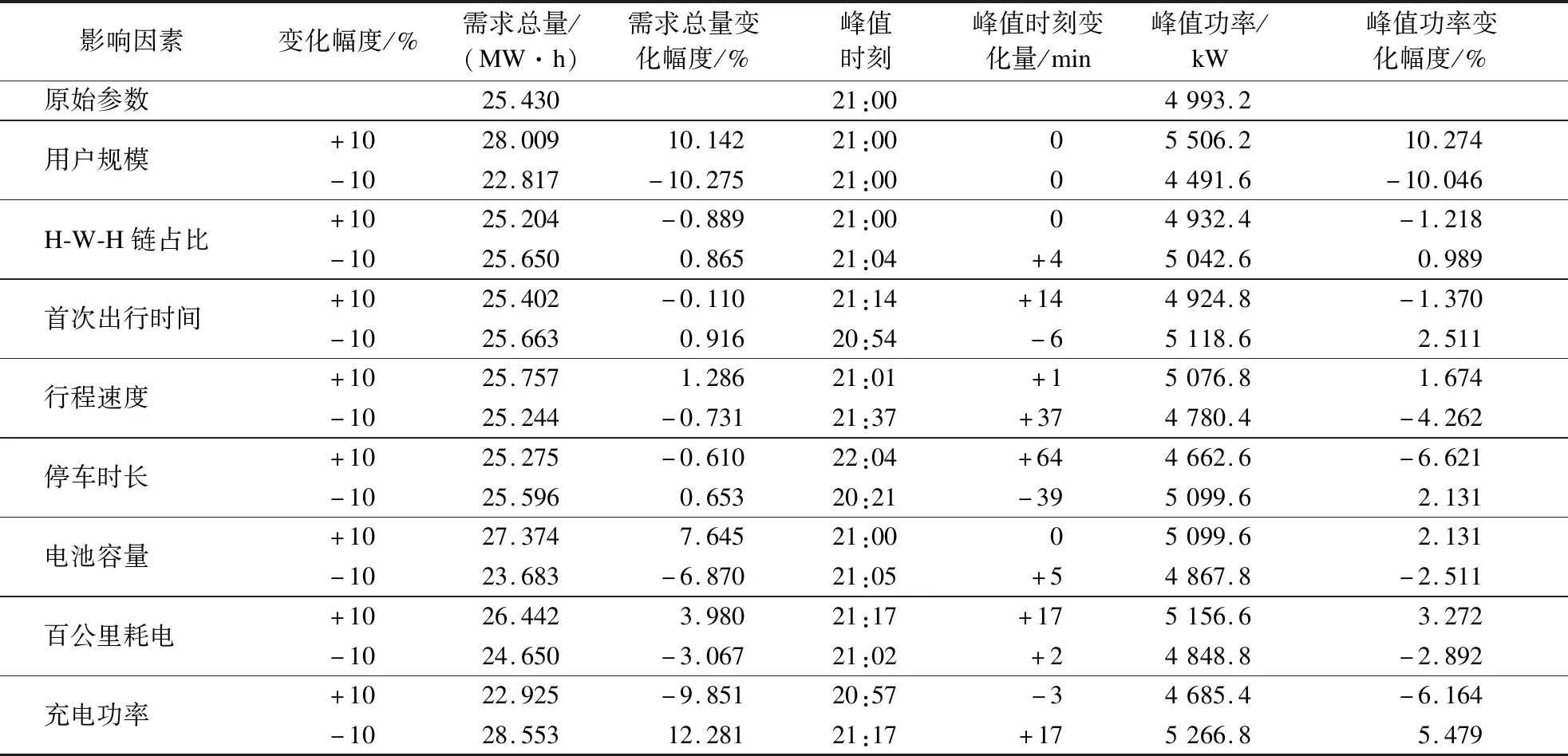
表5 居住区充电需求影响因素敏感性分析结果
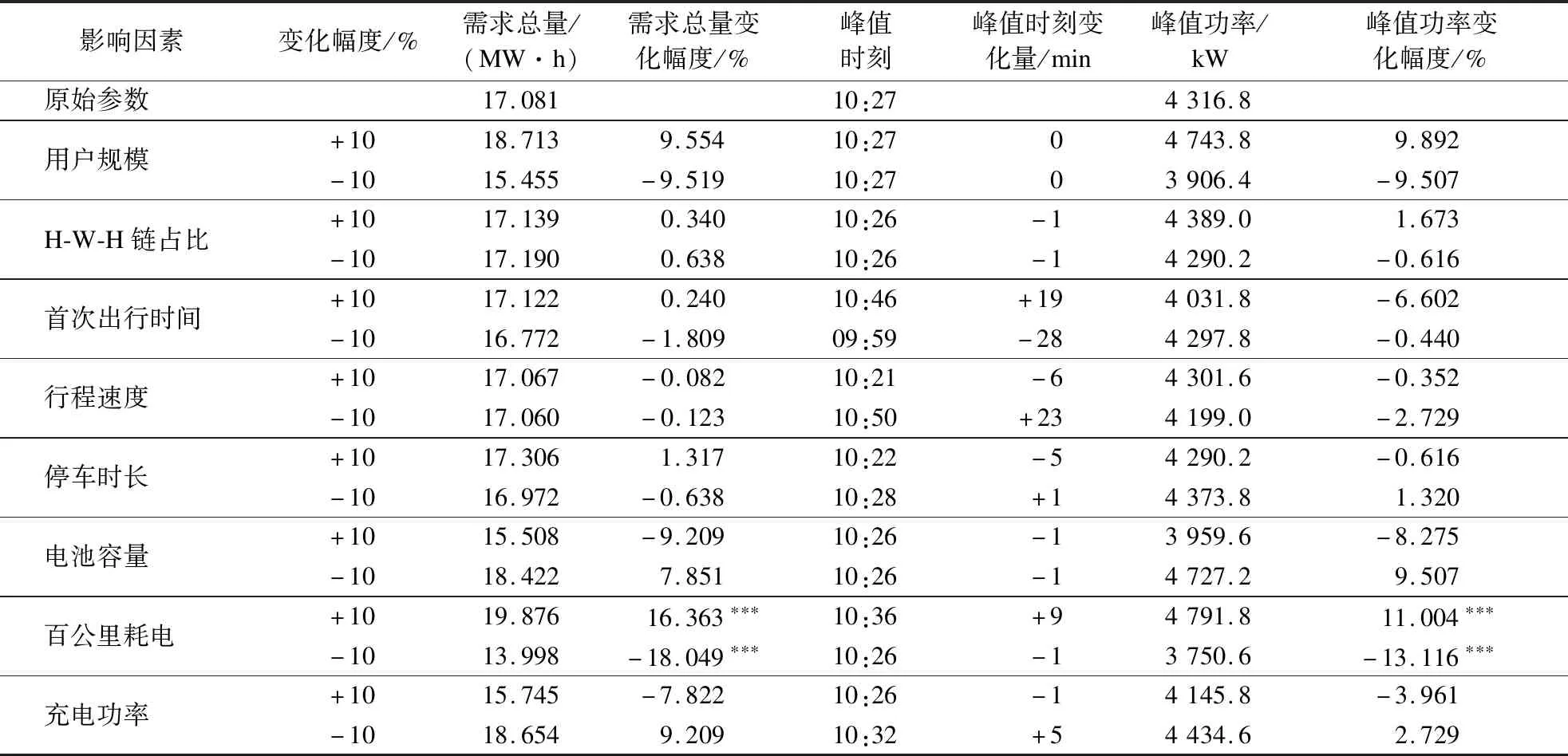
表6 非居住区充电需求影响因素敏感性分析结果
首次出行时间、行程速度、停车时长的变化对于各区域充电需求与峰值功率有轻微影响,而主要影响的是充电高峰出现的时间.用户在各区域的充电高峰时刻随首次出行时间提前而相应提前,随其延后而延后.行程速度提高对充电高峰时刻影响不大,而行程速度变缓会使各区域充电高峰时刻显著延迟.当停车时长延长时,非居住区用户充电意愿增强,导致其充电需求总量有所上升,但对峰值时刻影响不大;在居住区,由于其充电需求更多转移到非居住区,其峰值功率明显下降,又由于返程时间延后而充电高峰时刻延后;反之则变化情况相反.
当电池容量提升10%时,用户充电需求总量与峰值功率在居住区会显著上升,而在非居住区会显著下降,而各区域高峰时刻几乎不变.这是由于车辆续驶里程提升,用户更少产生刚性与弹性充电需求,因此在出行链中间目的地的充电需求减少,回家后要充更多电才能充满;而电池容量降低时,情况则完全相反.
百公里耗电量的增加会导致用户在各区域的充电需求总量、峰值功率相应升高,反之亦反.此外,百公里耗电量的增加还会使充电高峰时刻略微延后,这是由于耗电量提升导致用户充电次数增多、充电时间延长;然而,相比之下百公里耗电量减少对于充电功率峰值时刻几乎没有影响.
最后,充电功率的提升可以缩短充电时长,使用户集中于某一时刻充电的比率降低,从而使得各区域峰值功率有一定幅度降低,用户的充电需求总量也有显著减少,而对峰值时刻几乎无影响.而充电功率降低会导致用户充电需求总量与峰值功率显著上升,且居住区充电高峰时刻显著延后.
综上所述,用户规模、出行链占比、电池容量、百公里耗电、充电功率主要影响充电需求量与峰值功率,而首次出行时间、行程速度、停车时长主要影响充电高峰时刻.其中,对于居住区的充电需求总量与峰值功率而言,影响最显著的是用户规模,对居住区峰值时刻影响最显著的因素是停车时长;对于非居住区充电需求总量与峰值功率而言,影响最为显著的因素是百公里耗电,而对非居住区峰值时刻影响最显著的是首次出行时间.
3.4 考虑不同车型的充电需求变化分析
本文提出的充电需求预测方法在假设用户出行链相对固定、行程特征不变的条件下可适用于不同的车型.考虑到荣威E50是较早期研发的新能源车型,与目前电动汽车电池技术水平差距较大,为分析不同车型用户的充电需求时空分布变化,现以荣威Ei5车型(电池容量61.1 kW·h,每百公里耗电13.3 kW·h,充电功率6.4 kW)进行模拟仿真,并将结果与E50用户进行对比,结果如图9所示.
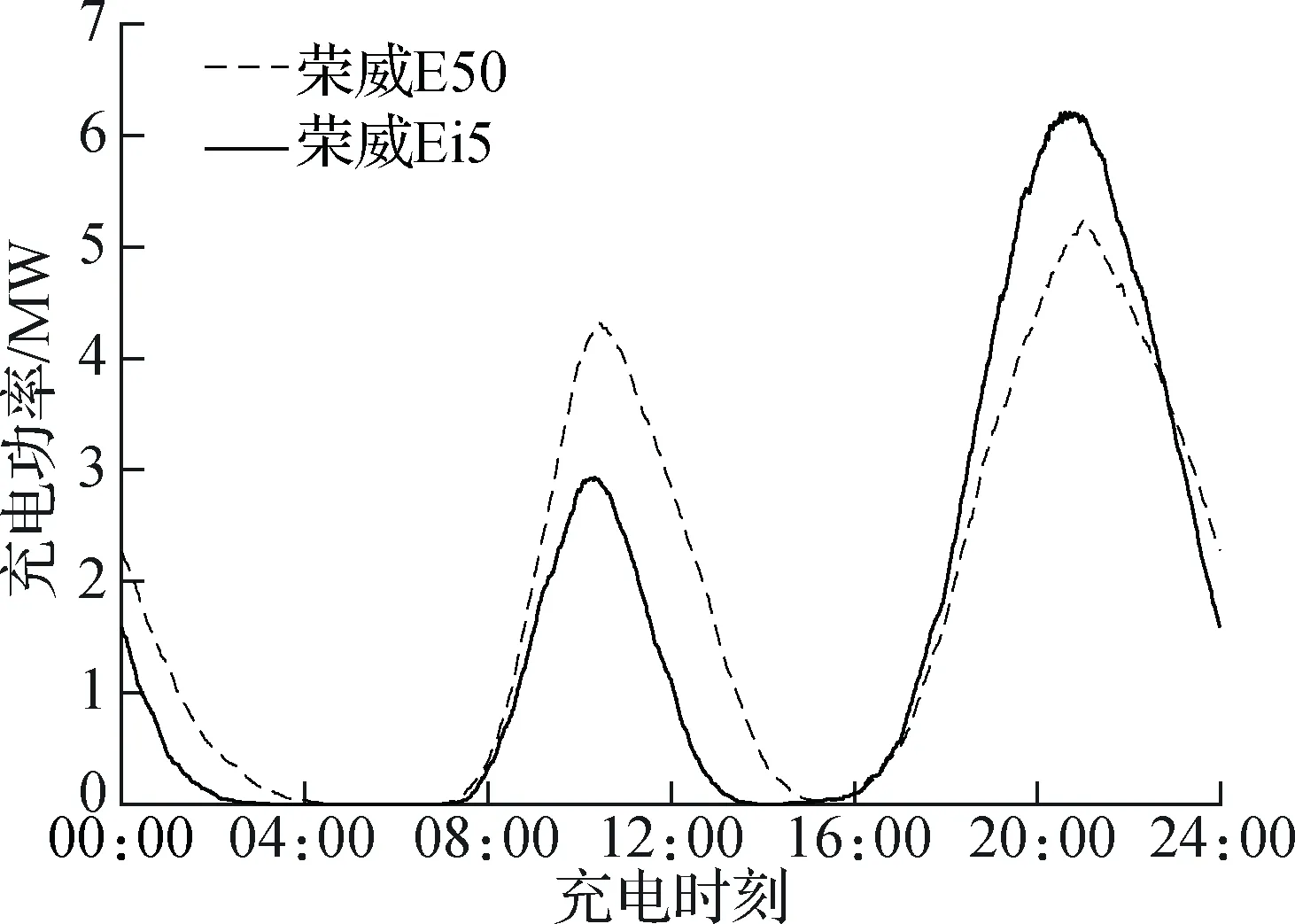
(a) 工作日区域充电需求总负荷曲线
结果显示,Ei5用户在仿真过程中共产生充电需求2 651次,行程途中充电次数为零,充分体现了其续驶里程长、电耗低的优势,2种车型用户在区域内的充电需求曲线如图9(a)所示.Ei5用户的充电需求总量为37 503 kW·h,相比E50用户减少了11.8%;由于假设用户遵循相同的出行行为与充电决策模式,因此2种车型充电需求曲线的变化趋势相似,Ei5用户充电需求在晚上20:48达到最高峰6 205 kW,于上午10:21到达次高峰2 932.1 kW,最多有965辆车同时充电.
2种车型用户在不同用地类型的充电需求如图9(b)所示.在居住区,Ei5用户的峰值充电功率为6 134.2 kW,而最大同时充电用户数仅为954;相比之下,由于Ei5用户充电需求较少且充电功率更大,因此夜间充电的用户数较少、持续时间较短,所有用户于凌晨03:15完成充电,比E50用户提前了约1.5 h.Ei5用户在工作区的最高需求功率为2 932.1 kW;相比于Ei5车型,E50车型电池容量更低、运行耗电更大,用户更容易产生刚性充电需求或有更大概率选择弹性充电,因此其充电用户数更多、需求总量更大、功率负荷更高.休闲区Ei5用户充电功率高峰为192.9 kW,仅最多30辆车同时充电;Ei5用户在休闲区的充电需求曲线相比E50用户具有峰值功率低、持续时长短等特点.
Ei5用户各功能区高峰时刻区域路网充电需求的空间分布如图10所示,其分布特征与E50用户基本相似,区别在于其工作区高峰时刻充电功率相对较小.
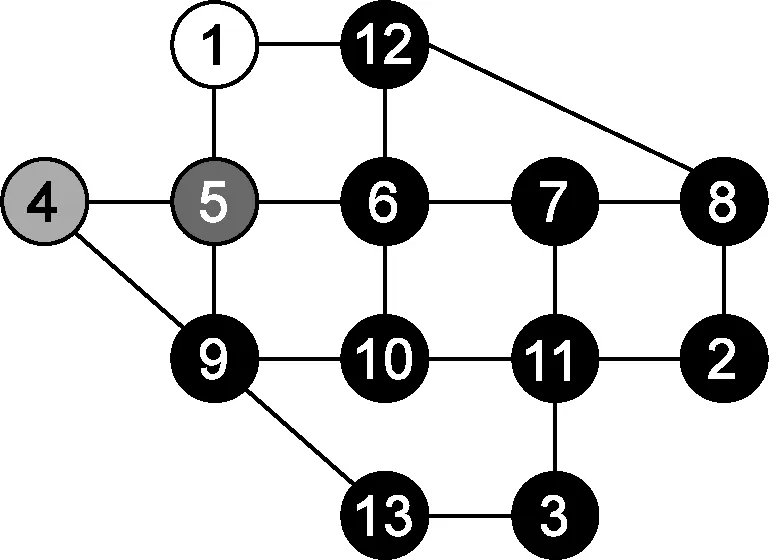
(a) 居住区高峰20:48
经对比发现,随着电动汽车电池技术水平的提高,用户在出行链中间目的地产生的充电需求将减少,充电持续时间将缩短,能够缓解其里程与充电焦虑.
4 结论
1) 本文依据电动汽车使用数据,基于用户出行-充电行为链构建了其出行时空转移与模糊充电决策模型,建立了电动汽车充电需求时空分布的精细化预测方法,其时间分布预测精确到分钟,空间需求预测精确到路网节点.
2) 算例分析结果表明,居住区充电量占需求总量的59.8%,并于21:00达到功率最高峰;工作区充电需求量占比为35.7%,充电高峰时刻为上午10:27;休闲区充电需求最少,占比为4.5%,充电高峰时刻为18:50.预测结果符合用户使用电动汽车出行和充电的基本时空规律.
3) 影响因素敏感性分析发现,在居住区,用户规模对充电需求总量与峰值功率影响最显著,停车时长对峰值时刻影响最显著;而在非居住区,百公里耗电对充电需求总量与峰值功率影响最显著,首次出行时间对峰值时刻影响最显著.
4) 不同车型充电需求变化分析发现,Ei5用户相比于E50用户充电需求总量减少11.8%,夜间充电完成时间提前1.5 h,电池技术水平的提高使用户在出行链中间目的地产生的充电需求减少,充电持续时间缩短.
5) 后续研究可以进一步考虑通过软硬件结合的方式提升模型的适用性匹配更多的路网规模.进一步探讨多样化的车型、充电设施与充电模式,以及用户群体与其行为模式异质性,建立内涵更丰富、更具针对性的充电需求分析模型,并对预测模型的有效性进行验证.
