基于复合降噪的LSTM综合模型的股指预测研究

杨亚男,叶善力

(浙江科技学院 理学院,杭州 310023)

由于股票市场的数据具有非线性且不稳定的特点,其数据预测比较困难。传统时间序列模型和机器学习方法是当前金融市场股票价格预测最常用的两类方法,其中,传统时间序列模型的预测方法主要有自回归移动平均模型、广义自回归条件异方差模型等[1-2]。常月等[3-4]证明传统组合模型比单一模型的预测精度更高、预测误差更低。如今,机器学习方法在金融领域备受关注且被广泛应用,主要包括支持向量机回归、卷积神经网络、循环神经网络(recurrent neural network,RNN)和长短期记忆神经网络(long-short-term memory neural network,LSTM)等[5-7]。其中最受青睐的还是LSTM模型,杨青等[8-9]验证了通过改变LSTM模型的参数可以达到比其他模型更优的预测精度。

随着人们对股市建模精度要求的提高,单一预测模型已经无法通过改进模型本身提高预测精度。1998年,Huang等[10]提出经验模态分解(empirical mode decomposition,EMD),将其应用于处理非线性、非平稳时间序列的方法。为了改进EMD分解后模态混叠问题,Wu等[11-13]相继提出了集成经验模态分解(ensemble empirical mode decomposition,EEMD)、互补集成经验模态分解(complementary ensemble empirical mode decomposition,CEEMD)和自适应噪声完备经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN)等分解方法,这样既提高了分解效率,又降低了计算误差。在分解算法的基础上,姚洪刚等[14-15]提出了EMD-LSTM和CEEMDAN-LSTM混合模型,证明其比单一LSTM模型预测误差更低。张培玲等[16-17]针对单一分解方法,提出了CEEMDAN-小波阈值(wavelet threshold,WT)和小波变换-EEMD混合分解方法,证明其比单一分解方法去噪更优。为了进一步提高股票市场的预测精度,我们提出了基于CEEMDAN-WT去噪的复合降噪的LSTM综合预测模型。

1 相关模型与方法

1.1 EMD模态分解

EMD适合于非平稳信号的分析,将原始信号分解成不同本征模态函数(intrinsic mode function,IMF)。IMF分量的确定需要满足以下两点要求:一是极值点要求,即至少包括一个极大值点和一个极小值点;二是局部最大和局部最小的上下包络线均值为零。EMD的具体分解方法如下:

1) 对原始信号X(t)确定局部最大值点和局部最小值点。

2) 利用3次样条函数对这些局部极大值点进行插值得到X(t)的上包络线,同理得到局部极小值点下包络线,并求出上下包络线的均值

(1)

式(1)中:u(t)为上包络线;l(t)为下包络线。

3) 分量h1(t)=X(t)-m(t),检查h1(t)是否满足IMF的条件,如果满足,h1(t)则为第一个IMF,否则对h1(t)按照X(t)做同样处理。重复上述迭代过程直到hk(t)符合IMF的条件或达到停止标准,停止标准的计算值为

(2)

式(2)中:hk-1(t)为第k-1个IMF分量;hk(t)为第k个IMF分量。当ySD小于某一特定值即达到停止标准,其中特定值一般在[0.2,0.3]选取。

1.2 CEEMDAN模态分解

EMD虽然可以分解任意信号,但模态混叠,针对这个问题,Wu等[11]提出加入白噪声的EEMD改进方法。虽然模态混叠得到改善,但是出现了新的问题,EEMD分解后会包含残余噪声,从而大大降低了重构信号的预测精度。因此Torres等[13]提出来CEEMDAN方法,通过在原序列加入自适应白噪声,使EEMD方法得到了进一步的完善,提高了分解的速度,重构误差几乎趋向于零。CEEMDAN具体算法步骤[18]如下:

1) 产生含噪声的原序列:

Si(t)=S(t)+ε0ωi(t)。

(3)

式(3)中:S(t)为原始时间序列;ωi(t)为服从正态分布N(0,1)的高斯白噪声;ε0为噪声标准差;i为添加噪声的次数。

2) 利用EMD对Si(t)=S(t)+ε0ωi(t)进行分解,得到第一个IMF:

(4)

式(4)中:yIMF1为EMD分解后第一个IMF分量;yIMFi为EMD分解后多个一阶分量。

3) 计算第一阶段残差:

r1(t)=S(t)-yIMF1。

(5)

式(5)中:r(t)为残差;r1(t)为第一阶段残差。

4) 对序列r1(t)+ε1E1(ωi(t))进行分解,得到第二个IMF:

(6)

式(6)中:yIMF2为第二个IMF分量;Ei(·)为EMD分解后第i个分量IMF;εi为噪声标准差。

5) 重复上述步骤,直到最后的残余分量不再进行分解,则为最后的残差,公式如下:

(7)

式(7)中:yIMFj为原始时间序列分解后得到的不同尺度分量。

1.3 小波阈值去噪

小波阈值去噪是通过小波对原始信号分解得到小波系数,采用恰当的阈值后,分别对系数和阈值的大小做对比处理及小波重构,最终达到降噪的目的。硬、软阈值函数是小波阈值去噪方法中最常见的两种阈值函数。硬阈值去噪方法是如果给定的阈值大于小波系数的绝对值,则为零;否则系数不变。硬阈值计算公式如下:

(8)

软阈值去噪方法是如果给定阈值不大于小波系数的绝对值,则令其都减去阈值;否则,为零。软阈值计算公式如下:

(9)

式(8)～(9)中:ω为小波系数;λ为给定的阈值。

1.4 长短期记忆神经网络

LSTM模型是一种特殊的RNN模型,不仅拥有了RNN模型的大部分特性,同时还解决了RNN梯度爆炸问题,即对远距离梯度形成依赖关系。LSTM模型采用控制门的方式让信息选择性通过,而信息的更新和维持则需要依靠输入门、遗忘门和输出门来完成。LSTM结构如图1所示。

图1 LSTM结构

xt是LSTM单元在的输入值,ht和ht-1分别是LSTM在时刻t和时刻t-1的输出值,而ct是LSTM记忆单元时刻t的值。LSTM模型具体算法步骤如下：

1) 计算遗忘门ft的值。

ft=σ(Wf·[ht-1,xt]+bf)。

(10)

式(10)中:Wf为遗忘门对应的权重矩阵;bf为遗忘门对应的偏置项。

2) 计算输入门it的值。

it=σ(Wi·[ht-1,xt]+bi)。

(11)

式(11)中:Wi为输入门对应的权重矩阵;bi为遗忘门对应的偏置项;σ为sigmoid函数。

(12)

式(12)中:Wc为候选记忆单元对应的权重矩阵;bc为候选记忆单元对应的偏置项;tanh为双曲正切函数,起激活作用。

4) 计算记忆单元ct当前时刻的值。

(13)

式(13)中:ct-1为LSTM上一单元的状态值。

5) 计算输出门ot的值。

ot=σ(Wo·[ht-1,xt]+bo)。

(14)

式(14)中:Wo为输出门对应的权重矩阵;bo为输出门对应的偏置项。

6) 最后计算LSTM的输出值ht。

ht=ot×tanh(ct)。

(15)

2 面向股市的建模思路

从上述分析我们可以看出CEEMDAN在数据分解上有较大的优势,而分解后的高频分量,可以利用小波阈值去噪进一步降噪,从而降低原序列的误差,并且LSTM在时间序列预测中对长期依赖性的学习能力非常突出。基于此,试验构建了CEEMDAN和小波阈值复合降噪的LSTM混合预测模型。CEEMDAN-WT-LSTM建构流程如图2所示,其基本框架分为四个阶段:原始股指分解、高频分量优化、各序列预测和集成预测结果。具体步骤如下:

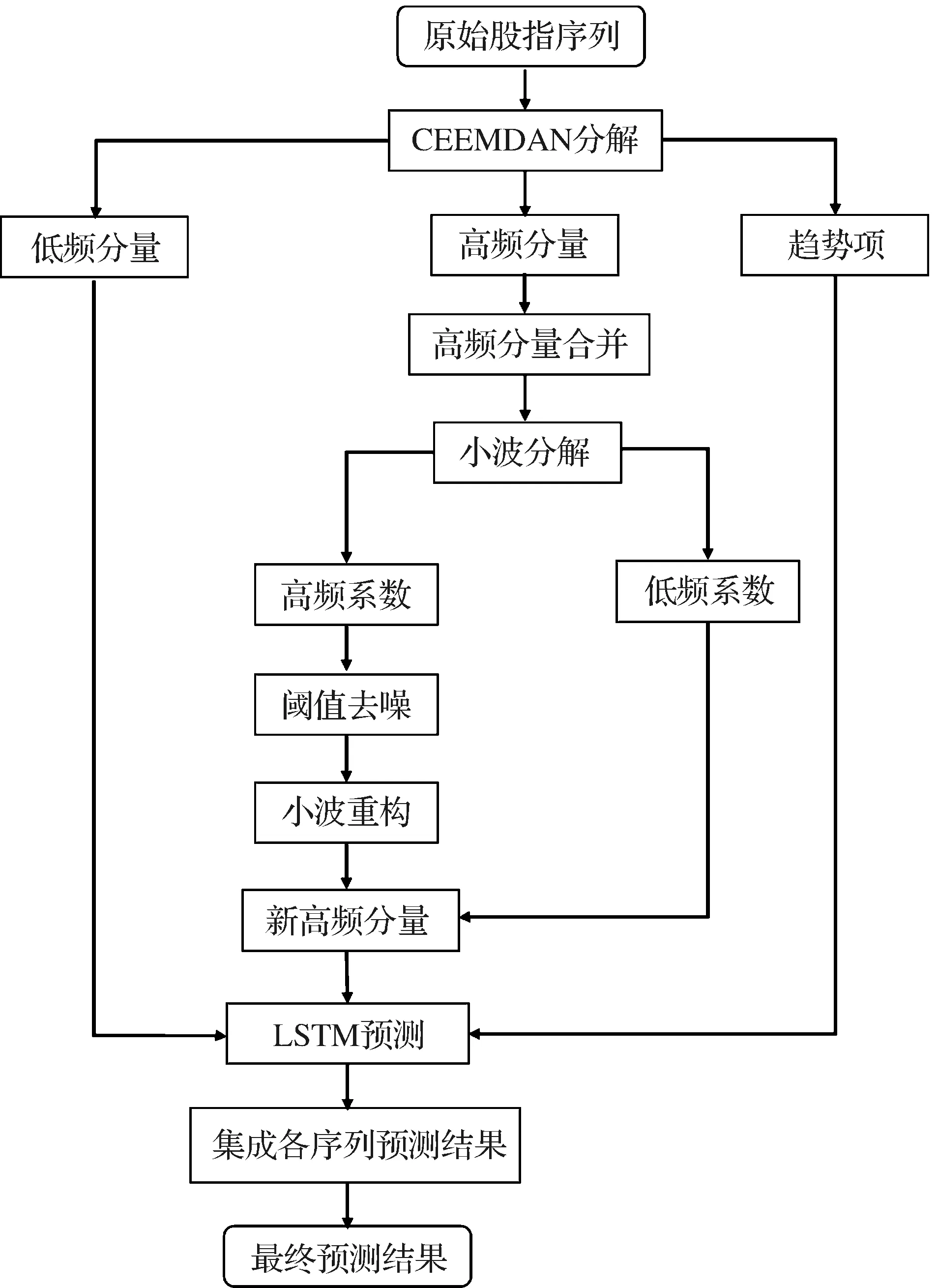
图2 CEEMDAN-WT-LSTM建构流程

1) 基于CEEMDAN将原始股指S(t)分解成res(residual,趋势项)与多个IMF分量；

2) 将所获的IMF通过单样本t检验的方法来确定高频分量和低频分量,将检验过的高频分量合并为一个新分量,记为IMFS；

3) 利用小波阈值对高频分量IMFS去噪,得到新高频分量,记为IMFH；

4) 利用LSTM模型分别对高频分量IMFH、低频分量和趋势项进行建模预测,得到各分量的预测值,最后求和即为最终预测值。

3 试验分析

3.1 样本数据

选取上海证券交易所股价综合指数(Shanghai Stock Exchange Composite Index,SSEC,简称上证指数)、深圳证券交易所成份股价指数(Shenzhen securities component index,SZI,简称深证成指)为数据建模基础,因上证指数和深证成指对投资者具有重要的参考价值,即通过对上证指数和深证成指的预测来判断股票市场变化的趋势。由于这两种股票指数的模型构建方法相似,故仅以上证指数为代表进行研究分析,深证成指不再具体介绍,只在最后试验结果中体现。

选取2015年1月5日至2021年5月31日之间上证指数的收盘价(来源为网易财经),对数据进行剔除空值,重新排序等预处理,共计1 560个样本作为预测模型的原始数据。2020年10月20日之前共1 410个数据作为训练集,2020年10月20日至2021年5月31日之间共150个数据作为测试集,以此分析预测的效果。

3.2 复合降噪分析

对原始股指序列添加20 dB的高斯白噪声,合成新的加噪股指序列。对此加噪合成股指序列分别采用小波阈值去噪和CEEMDAN-WT去噪这两种不同的算法进行去噪。这两种算法的优劣主要通过信噪比(signal-to-noise ratio,SNR)和均方误差(mean-square error,MSE)来进行标准评价,SNR和MSE的计算公式分别如下:

(16)

(17)

式(16)～(17)中:x(i)为去噪后的数据;y(i)为原始序列数据;n为数据的长度。

根据SNR和MSE的评判标准,SNR值越大,MSE值越小,则评价结果越优。表1为SSEC在不同噪声强度下去噪性能指标数据,从数据对比可以看出,CEEMDAN-WT去噪的效果要优于单一小波阈值去噪。噪声强度从6 dB增加到20 dB,两者的信噪比都呈增加趋势,均方误差都呈下降趋势;但是对于同一噪声强度,CEEMDAN+WT去噪的信噪比明显高于小波阈值去噪,均方误差也明显小于小波阈值去噪。比如当噪声强度为20 dB时,CEEMDAN+WT去噪的信噪比和均方误差分别为21.091 5和0.051 3,比小波阈值去噪的信噪比提高了4.93%,比其均方误差下降了22.51%。因此,CEEMDAN-WT去噪算法的去噪效果更好一点。

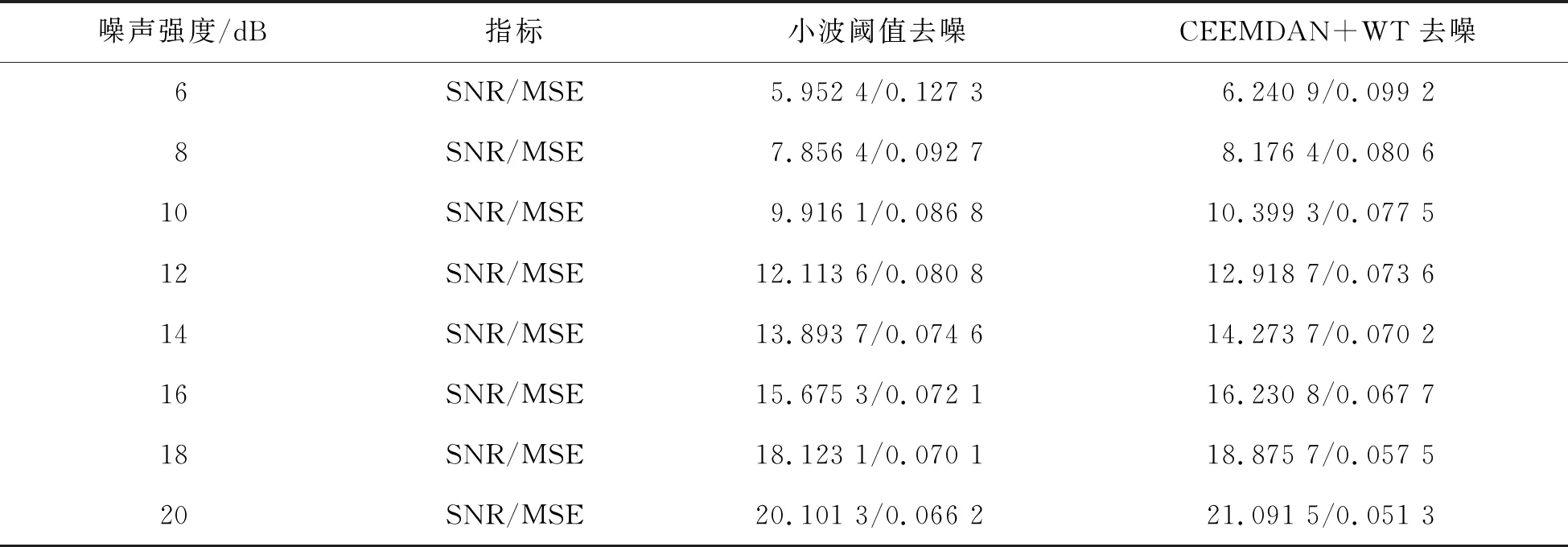
表1 SSEC在不同噪声强度下去噪性能指标数据

3.3 CEEMDAN分解

3.3.1 基于CEEMDAN的股票指数的序列分解

上证指数的CEEMDAN分解结果,如图3所示。上证指数的股票原始序列通过CEEMDAN算法可以分解为一个趋势项和7个IMF分量。将IMF1至IMF7从高频分量到低频分量依次排列,其波动的频率逐渐降低;对于高频分量,随着频率的降低,它对原始数据的影响逐渐增强。

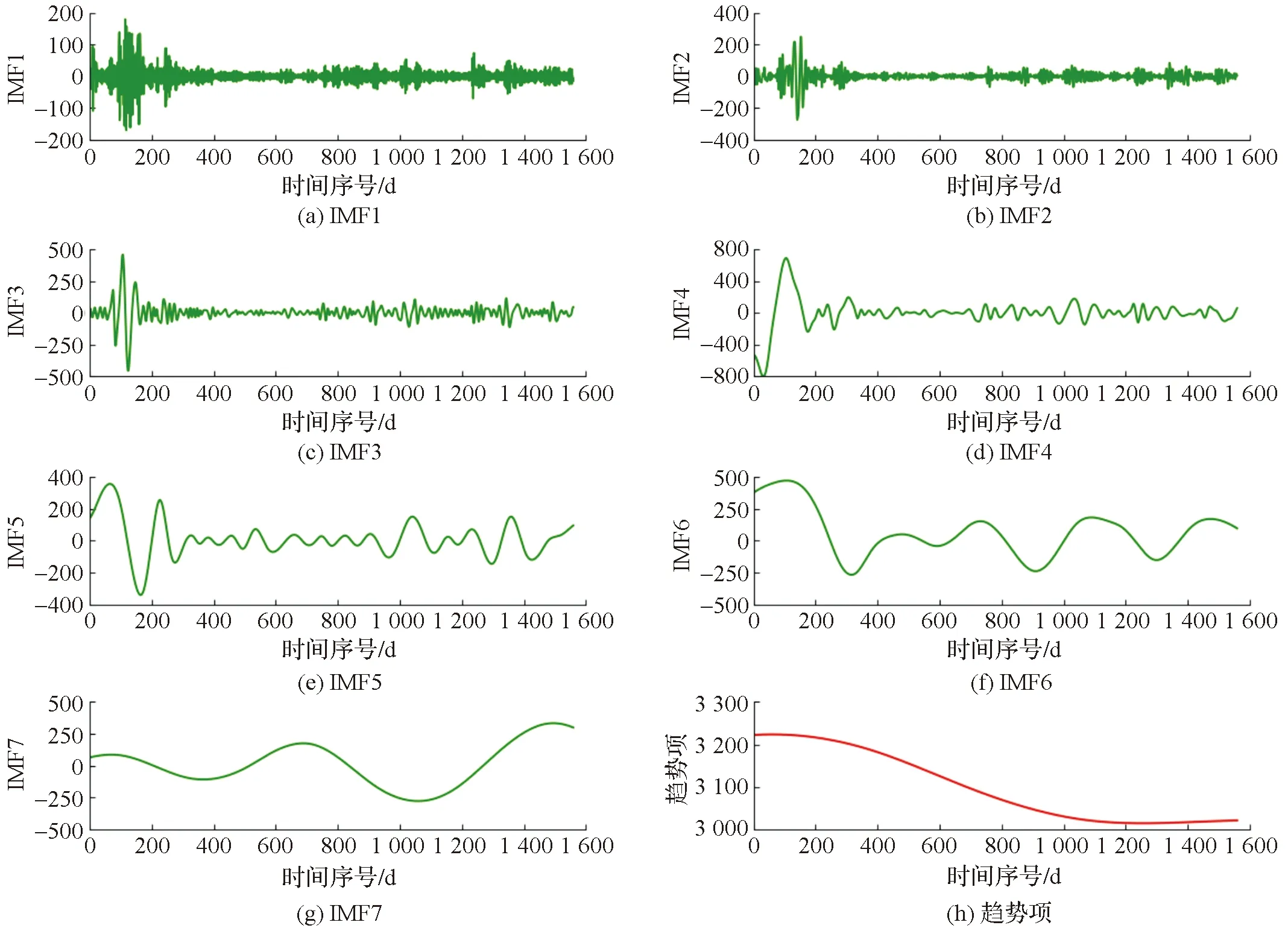
图3 上证指数的CEEMDAN分解结果

3.3.2 高低频的确定

高频分量和低频分量的确定主要通过统计学中单样本t检验来判断。SSEC训练集序列基于CEEMDAN分解的各分量单样本t检验见表2。从表2中可知,单样本t检验,IMF1的t检验值为0.942,显著性(双尾)的数值为0.346大于0.05,在95%的置信区间下,不拒绝原假设,即IMF1均值与0没有差异。同理可以判断IMF2、IMF3、IMF4与IMF1一样,其显著性(双尾)的数值均大于0.05,即均值与0没有差异,从而确定IMF1至IMF4均为高频分量,其主要反映随机波动对股票指数造成的影响。类比IMF1的分析过程,IMF5的t检验值为4.536,显著性(双尾)的数值为0.00小于0.05,在95%的置信区间下,拒绝原假设,即IMF5的均值与0存在显著差异;同理IMF6和IMF7与IMF5判断一样,其显著性(双尾)的数值均小于0.05,即均值与0存在明显差异且都不相同,因此把IMF5、IMF6、IMF7视为低频分量,其主要体现不同的周期性波动对股票指数的影响。趋势项则主要代表股票指数的长期趋势。

表2 SSEC训练集序列基于CEEMDAN分解的各分量单样本t检验

3.4 小波阈值去噪

从图3上证指数CEEMDAN分解结果中可以看出高频分量仍然存有噪声,因此先对IMF1至IMF4进行求和得到高频分量之和IMFS,再利用小波阈值去噪对高频分量IMFS进行去噪处理。选取消失矩为3的Daubechies小波基函数,并采用3层分解结构对IMFS进行分解,选择启发式软阈值进行小波重构。小波阈值去噪前后的高频分量对比见图4。从图4可看出,高频分量经小波阈值去噪后,降噪效果较好。

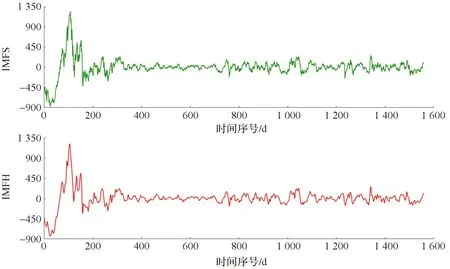
图4 小波阈值去噪前后的高频分量对比

3.5 基于LSTM建模

正如前文所述,CEEMDAN将SSEC分解为4个高频分量,3个低频分量和一个趋势项,这4个高频分量合并后通过小波阈值去噪优化形成新分量IMFH;然后利用LSTM模型对各序列进行预测建模,主要采用两层LSTM结构层,其中还设置了一个随机失活层,防止数据出现过度拟合的问题。经过反复试验后,模型的参数设置最终确定为:每层神经元的个数为64,每轮训练样本的个数为64,迭代次数为500,损失函数为平均绝对误差,优化器为adam,时间步长为10。

模型搭建完成后,我们开始用训练好的模型进行预测,同时为了消除模型的偶然性,分别对各分量进行10次预测试验,并取10次预测结果的平均值,最终的试验结果即为各分量的预测结果,其计算公式如下:

(18)

3.6 评价指标

模型评价指标[19]包括平均绝对误差(mean absolute error,MAE)、均方根误差(root mean square error,RMSE)及决定系数R2,计算公式分别如下:

(19)

(20)

(21)

由于深证成指的建模预测过程与上证指数的构建完全相似,因此只展示最终的预测结果。为了验证CEEMDAN-WT-LSTM模型的性能,将其与LSTM模型、EMD-LSTM模型、CEEMDAN-LSTM模型和WT-LSTM模型进行试验对比,观察不同模型对上证指数和深证成指的预测效果。各模型对SSEC和SZI的预测效果比较分别见表3和表4,由表可知CEEMDAN-WT-LSTM模型在上证指数和深证成指上试验测试集上得到的MAE和RMSE均小于其他模型,R2分别为0.996 2和0.988 3,更趋于1;并且与其他模型对比后可知,CEEMDAN-WT-LSTM模型的拟合效果更好,预测误差更低。

表3 各模型对SSEC的预测效果比较

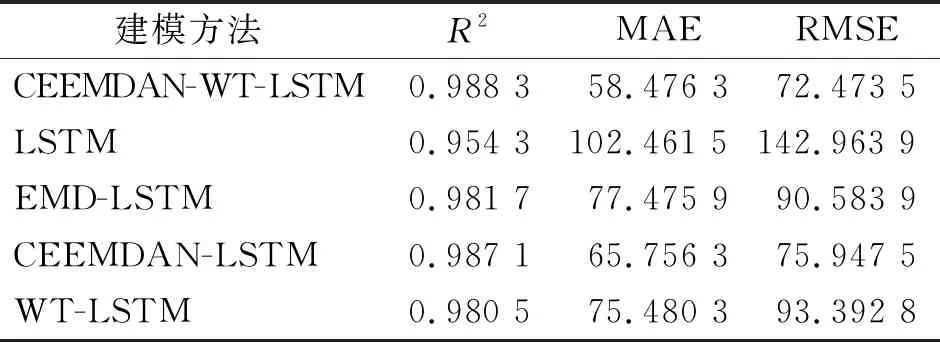
表4 各模型对SZI的预测效果比较

以上证指数为例,表现最优的CEEMDAN-WT-LSTM模型的MAE和RMSE值分别为13.187 1和16.252 3;表现第二的为CEEMDAN-LSTM模型,MAE值和RMSE值分别为16.347 9和19.976 1。相比CEEMDAN-LSTM模型,CEEMDAN-WT-LSTM模型的MAE和RMSE误差指标分别下降了19.33%和18.64%;与EMD-LSTM模型相比,该误差的下降幅度分别为39.42%和42.93%,改善效果明显;与WT-LSTM模型相比,该误差则分别下降了48.48%和48.65%,改善效果突出;与单一LSTM模型相比,该误差的下降幅度分别为49.47%和54.64%,改善效果颇为显著。这些数据证明原始数据经CEEMDAN分解和小波阈值复合降噪后的LSTM预测效果更佳,预测误差更小。

4 结 语

股票指数由于具有非稳定性、非线性的特点,传统预测模型已无法提高预测精度。本研究提出了CEEMDAN与小波阈值复合降噪的LSTM神经网络综合预测模型——CEEMDAN-WT-LSTM。首先通过引入CEEMDAN分解方法,提取序列波动信息;然后利用小波阈值去噪进一步降噪处理;最后再运用LSTM建立预测模型,求和即得最终预测结果。研究结果表明,在上证指数和深证成指的试验分析中,与其他模型相比,本研究提出的CEEMDAN-WT-LSTM模型对股票指数的预测具有更高的精度和稳定性,从而为金融时间序列数据预测提供了一种新方法。