跳跃机器人能量转换的主动控制与试验测试

王 建 缪 龙 张文祥 王树坤

南京工程学院机械工程学院，南京，211167

0 引言

跳跃机器人是智能机器人发展的重要组成部分，具有机动性能强、移动速度快、越障能力强等优点。目前，仿生跳跃机器人的结构大多为刚性结构，与生物的生理特性存在较大差异，因此它的能量转换效率和爆发力都无法与生物的真实肌肉系统相媲美[1]。对于利用简单机构(如弹簧)产生弹力进行弹跳的跳跃机器人而言，当线性弹簧尚未完全弹开即弹性势能尚未完全转换为动能时，机构已经提前开始离开地面，导致能量转换效率低。另外，电机最大输出转矩取决于弹簧最大限度压缩时的弹力，因此电机输出转矩无需达到最大值，即电机利用率低[2]。

利用仿生材料和新型驱动、新型机械结构可以提高跳跃机器人的能量转换效率。弹性驱动器是在传统的刚性驱动器中加入弹性元件以实现变刚度控制的驱动器,应用于机器人中可以为运动关节提供所需要的能量，并且可以实现能量调节，提高能量效率。文献[3-6]和文献[7-8]分别研究了串联弹性驱动器和并联弹性驱动器在跳跃机器人上的应用情况。此外，采用材料与驱动一体化的设计思路，利用智能材料的变形实现驱动已成为一个新的研究方向。相较于弹性驱动，智能材料驱动是利用材料在特定刺激下的刚度变化直接实现变刚度功能的，诸多新型材料，如形状记忆合金[9]、介电型EAP(电活性聚合物)[10]、硅树脂橡胶带[11]等都引起了学者的广泛关注，并已在跳跃机器人中得以应用，取得了不错的效果。在新型机械结构方面，主要是利用刚柔混合结构[12-14]、变结构的复合仿生机构[15]等改变储能大小、调整姿态角和缓解落地冲击，进而提高能量转换效率、改善弹跳性能、提高环境适应能力。相关研究资料表明，利用新型机械结构提高能量转换效率是跳跃机器人的发展趋势之一[1-2]。

对于跳跃机器人而言，主动控制其能量转换可以更有效地提高能量转换效率。所谓主动控制是指将能量转换曲线中的关键参数作为设计变量，反过来去构建跳跃机器人模型，以实现通过选择合理的能量转换曲线控制弹性势能和动能之间的转换。非圆齿轮可以实现复杂的非线性传动关系，它不仅可以用来调节转动速度和改变旋转方向，还可以调节工作机构的循环时间或周期，实现工作行程的等速运动和空回行程的急回运动，或在行程中增减速度[16]。如在心肺手术用供血泵中，由多段节曲线组成的非圆齿轮可以使滑块具有两个运动行程，一个是对应着心肺收缩期的快速前进行程，另一个是对应着心肺舒张期的慢速返回行程[17]。根据茶叶的加工工艺，牛石从等[18]设计的非圆齿轮可以实现在运动的初始阶段，速度在尽量短的时间内加速，然后进入一个相对较平缓的运动，最后在尽量短的时间内让茶叶停止运动。根据干草压捆机的压捆特性，雷昌毅等[19]设计的非圆齿轮可以实现小阻力阶段快速压缩、大阻力阶段以恒定的速度低速压缩。具有特殊运动规律的非圆齿轮应用于平流泵中，可以实现滑块机构的等速快退运动特性[20]。另外，学者在善于跳跃的伊苏斯虫(Issus)的后腿上发现了一种天然的非圆齿轮结构，尽管目前无法解释这种齿形奇怪的齿轮存在的原因，但至少证明了齿轮在跳跃昆虫的自然行为中起着一种功能性的作用[21]。这就促使人们探索利用特殊形状的非圆齿轮控制跳跃机器人能量的有效存储和释放的可行性，进而提高能量转换效率。鉴于此，本文拟建立一种跳跃机器人新构型，以实现利用非圆齿轮的啮合主动控制能量的有效存储和释放，进而控制弹簧的线性动力与非线性递增的弹跳动力之间的转换。

1 机构组成及运动原理

1.1 整体结构

图1所示为跳跃机器人整体结构模型，主要由前肢、后肢、主体支架和尾杆等部件组成。前肢用来支撑和连接，后肢提供跳跃的力和能量，主体支架除用于支撑和连接外，还可以安放驱动元件和传感器。

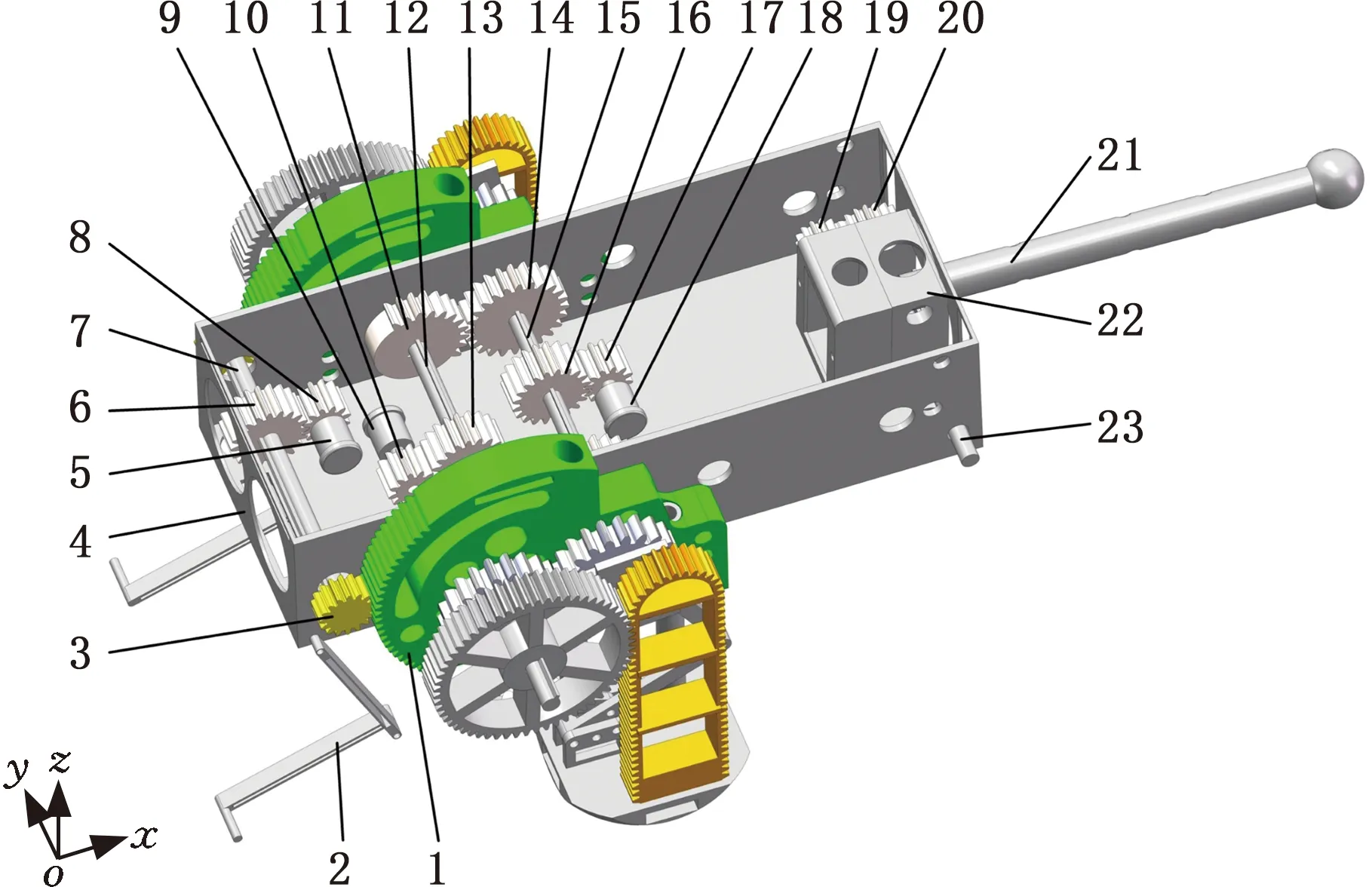
(a)机器人整体结构

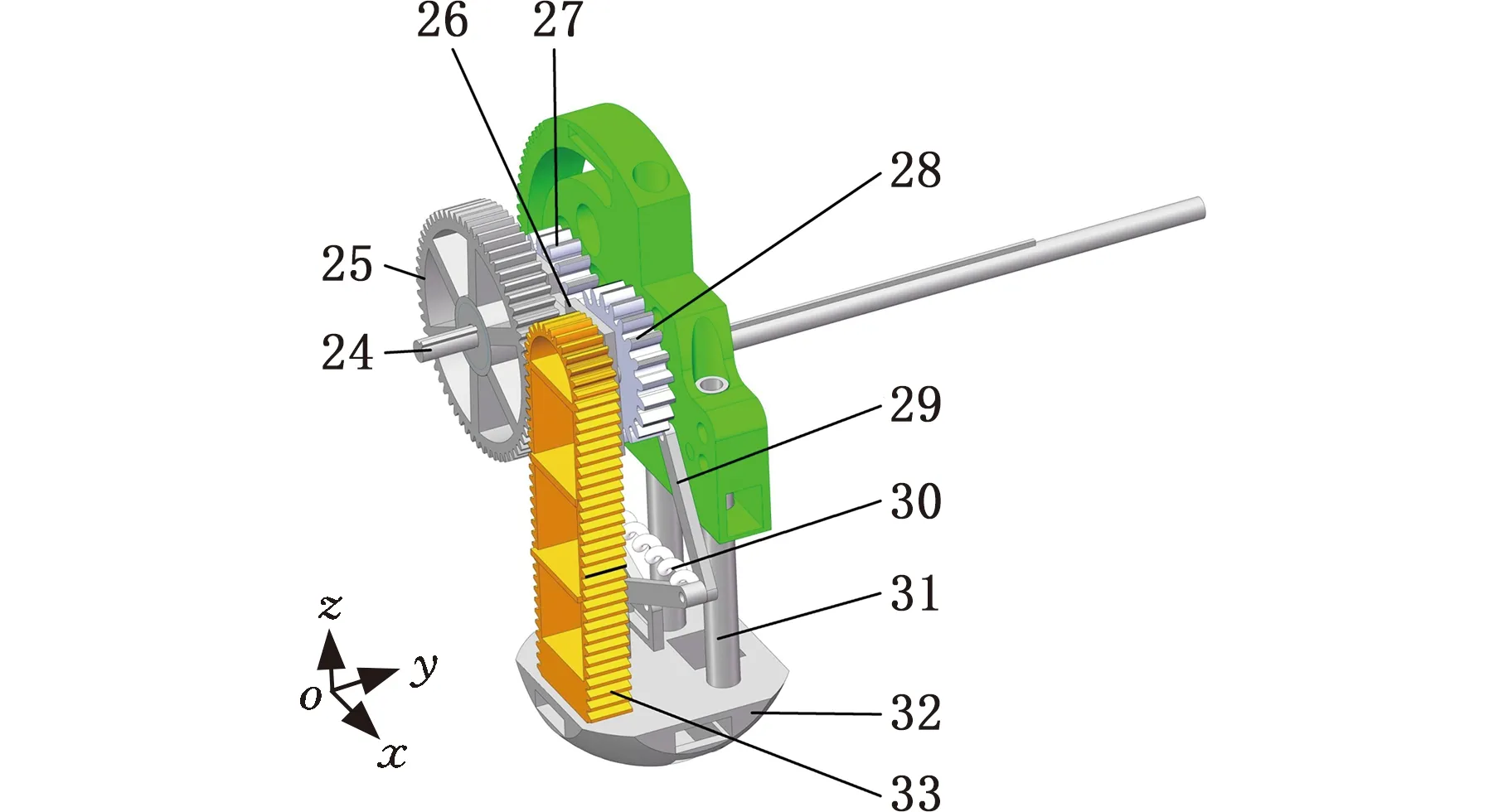
(b)机器人后肢结构1.转向盘 2.前肢 3.转向齿轮 4.主体支架 5.舵机一 6.转向输出齿轮 7.转向齿轮轴 8.转向输入齿轮 9.驱动电机 10.驱动输入齿轮 11.缺齿齿轮 12.驱动齿轮轴 13.驱动输出齿轮 14.小圆齿轮 15.释放齿轮轴 16.释放输出齿轮 17.释放输入齿轮 18.释放电机 19.小齿轮 20.大齿轮 21.尾杆 22.尾杆箱 23.尾杆齿轮轴 24.非圆齿轮输出轴 25.圆齿轮 26.系杆 27.非圆齿轮从动轮 28.非圆齿轮主动轮 29.菱形四杆 30.弹簧 31.导轨 32.脚部 33.齿条图1 跳跃机器人整体结构模型

在跳跃机器人结构中，释放电机18与释放输入齿轮17相连，释放输出齿轮16、小圆齿轮14和非圆齿轮主动轮28安装在释放齿轮轴15上；驱动电机9和驱动输入齿轮10相连，缺齿齿轮11和驱动输出齿轮13安装在驱动齿轮轴12上；圆齿轮25和非圆齿轮从动轮27安装在非圆齿轮输出轴24上。弹簧储能前，先进行姿态调整，驱动电机9转动，在驱动输入齿轮10和驱动输出齿轮13的啮合作用下，驱动齿轮轴12带动缺齿齿轮11转动，在缺齿齿轮11和小圆齿轮14的啮合作用下，与小圆齿轮14共轴线的非圆齿轮主动轮28转动，在非圆齿轮主动轮28与非圆齿轮从动轮27的啮合作用下，圆齿轮25沿齿条33运动。当缺齿齿轮11啮合到无齿部分时，驱动电机9停止，释放电机18开始工作，在释放输入齿轮17与释放输出齿轮16的啮合作用下，释放齿轮轴15带动非圆齿轮主动轮28转动，在非圆齿轮主动轮28与非圆齿轮从动轮27的啮合作用下，圆齿轮25沿齿条33运动。

1.2 能量转换方案及弹跳机理

图1中具有特殊运动规律的非圆齿轮27和28是控制能量转换的关键，图2为其啮合示意图。其中，主动齿轮的节曲线由AB、BC和CA组成，从动齿轮的节曲线由ab、bc和ca组成。当主动轮匀速旋转一周时，从动轮也会相应旋转一周，且做一次增速(AB/ab)、一次等速(BC/bc)和一次减速(CA/ca)运动。

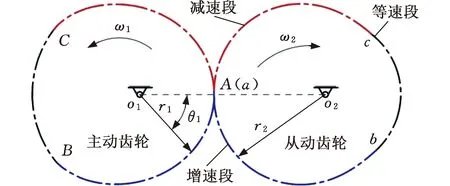
图2 具有特殊运动规律的非圆齿轮啮合示意图

图3为弹跳机理示意图，其中菱形四杆机构29铰接于主体支架4上，主从动非圆齿轮28和27分别通过轴承安装于释放齿轮轴15和非圆齿轮输出轴24上，且两轴之间通过系杆26连接，用于保证圆齿轮25与齿条33啮合而不会产生干涉。其弹跳原理为：在机器人起跳阶段，非圆齿轮从动轮27做增速传动，圆齿轮25和齿条33啮合于齿条的左侧(图1b所示位置)，在能量释放完的瞬间，增速传动结束，在腾空阶段，非圆齿轮从动轮27做等速传动，由于系杆26的作用，圆齿轮25和齿条33啮合于齿条的上部(齿条的圆弧部分)，而在着陆阶段，圆齿轮25和齿条33啮合于齿条的右侧，非圆齿轮从动轮27做减速传动，同时压缩弹簧存储能量，准备下一次弹跳。

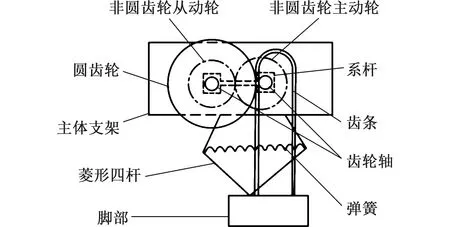
图3 弹跳机理

1.3 姿态调整方案及实现

在图1中，x、y方向分别为沿着尾杆和垂直于尾杆的方向，跳跃机器人在x方向的姿态调整由舵机来实现。如图1所示，舵机一5与转向输入齿轮8相连，转向输出齿轮6与转向齿轮3安装在转向齿轮轴7上。图4为姿态调整示意图，舵机一5提供动力到转向齿轮3，转向齿轮3与转向盘1啮合，当转向盘1转动一个小的角度时，后肢所有零部件同时转动一个相同的角度，以实现x方向的姿态调整，调整起跳角度后的示意图见图5。本方案中的舵机与电机之间的转动不是同步的，即当电机运行时，舵机停止运行，同样地，当舵机运行时电机停止运行，即姿态调整和跳跃不是同步进行的。

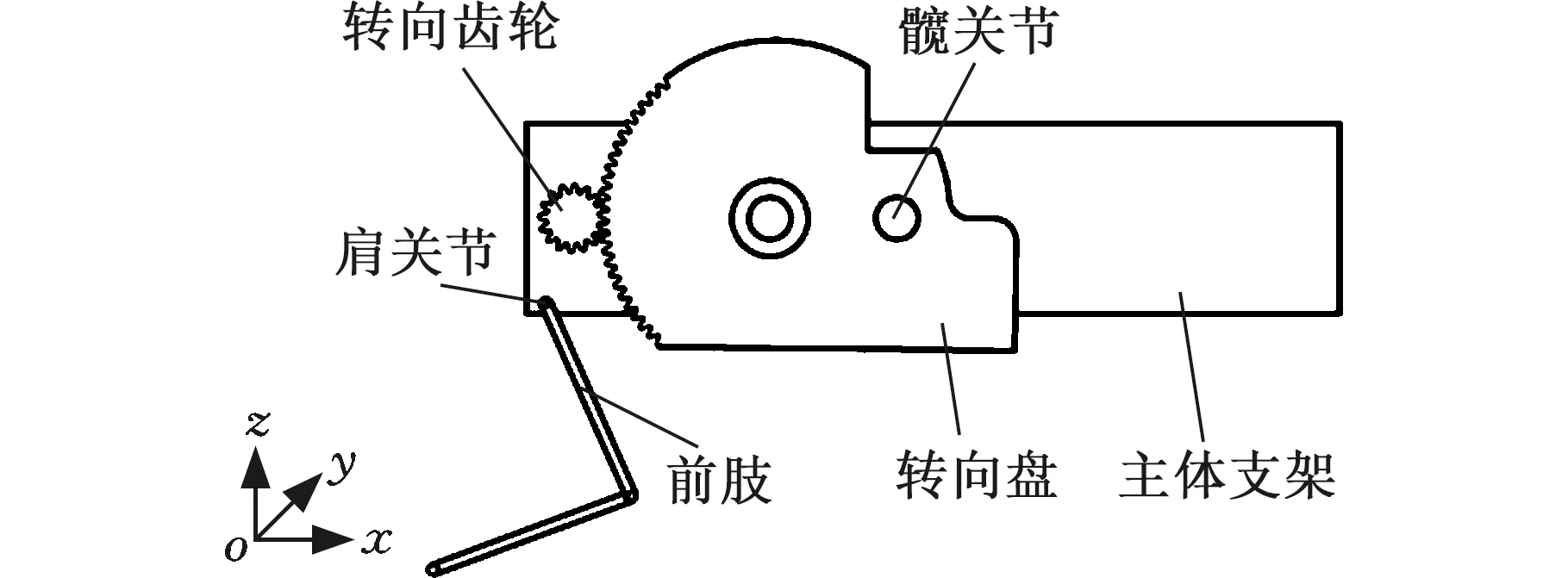
图4 沿x轴方向姿态调整原理

(a)沿x轴正方向调整起跳角度

(b)沿x轴负方向调整起跳角度图5 舵机一调整机器人起跳角度示意图

1.4 弹跳运动流程

跳跃机器人的弹跳运动流程如图6所示。首先，利用舵机一5调节身体姿态和起跳角度，然后驱动电机9正转(顺时针转)。在缺齿齿轮11有齿部分的啮合作用下，主体支架4和转向盘1沿导轨31向下滑动，弹簧30在菱形四杆机构29的作用下被拉伸，当缺齿齿轮11即将啮合到无齿部分时，跳跃机器人蓄能过程结束；在起跳阶段，缺齿齿轮11转到无齿部分，驱动电机9停止，释放电机18开始工作，与齿条33啮合的圆齿轮25沿齿条33向上转动。由于没有压力禁锢，弹性势能瞬间释放，机器人腾空；在着陆阶段，非圆齿轮从动轮27在系杆26作用下转动到齿条33另一侧，此时释放电机18停止工作，驱动电机9正转，继续带动圆齿轮25沿齿条33向下运动，压缩弹簧，存储能量，如果要重新开始下一个周期则进入准备阶段，否则跳跃过程结束。

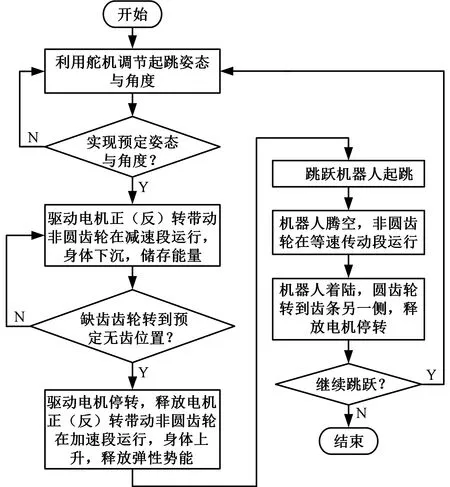
图6 弹跳运动流程图

2 能量转换主动控制及非圆齿轮设计

2.1 主动控制机理

由弹跳运动流程可知，非圆齿轮转动的三个阶段(增速传动段、等速传动段和减速传动段)分别对应着跳跃机器人运动的三个阶段(起跳、空中飞行和着陆)。而在上述三个运动阶段中，弹簧对应的状态为：在起跳阶段，弹簧释放弹性势能；在空中飞行阶段，弹簧处于自由伸缩状态；而在着陆阶段，弹簧拉伸储存弹性势能。因此，以主动齿轮的转角为横坐标，以弹簧的弹性势能为纵坐标，可以画出非圆齿轮转动过程与弹簧弹性势能的变化曲线，如图7所示。由图7可知，在主动齿轮一个完整的转动周期T内，0～θ11段为非圆齿轮增速传动段，在0点处弹簧的变形量最大，此时其储存的能量最多，当机器人增速传动结束，即在θ11时开始离开地面；θ11～θ13段为等速传动段，非圆齿轮做等速传动，弹簧在该阶段处于自由伸缩状态，机器人已经解除束缚进入腾空阶段(该阶段弹簧的伸缩不影响机器人的弹跳运动，因此对弹簧弹性势能的变化做了简化处理)；θ13～θ14段为减速传动段，在θ13处弹簧刚好恢复原长，非圆齿轮做减速传动，弹簧开始拉伸储存弹性势能，当到达θ14时，弹簧变形量最大，储能达到最大值。

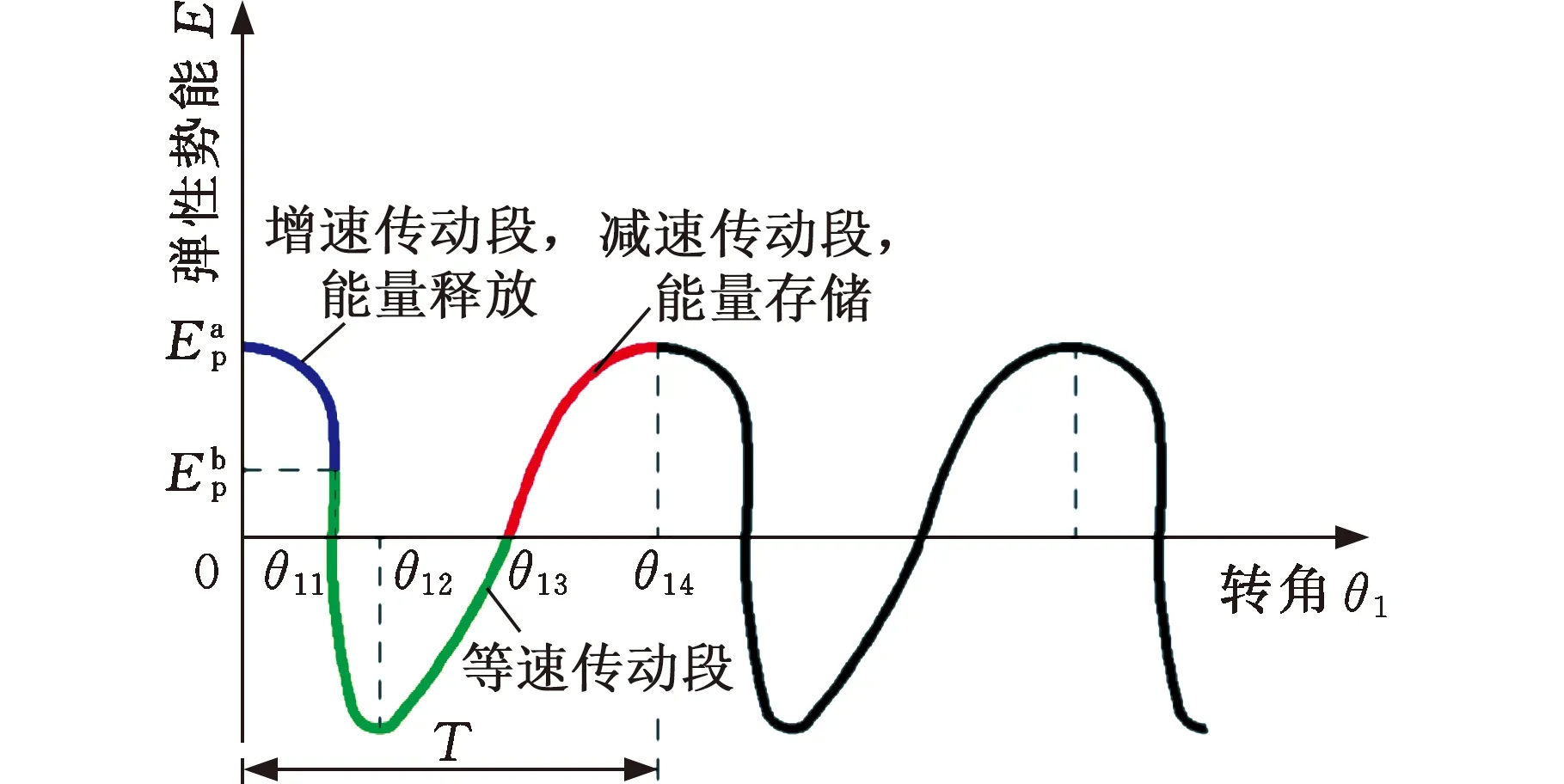
图7 弹性势能变化曲线

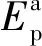
(1)

跳跃机器人的能量转换效率η可表示为

(2)

2.2 机器人起跳判据

要控制机器人离开地面时弹簧还存有的弹性势能大小，必须首先掌握机器人的起跳判断依据。不失一般性，将机器人简化为图8所示的质量-弹簧物理模型，其中弹簧位于两质量块中间，下质量块保持整体的平衡和稳定。在图8中，弹簧质量忽略不计，两质量块的质量分别是m1和m2，弹簧的弹性系数为k，原始长度为s0，变形量用s表示，机构的总质量用m表示。假设两质量块的质心分别为z1和z2，为了方便推导，令μ=m1/m，则整个机构的质心zc可表示为

zc=μz1+(1-μ)z2

(3)

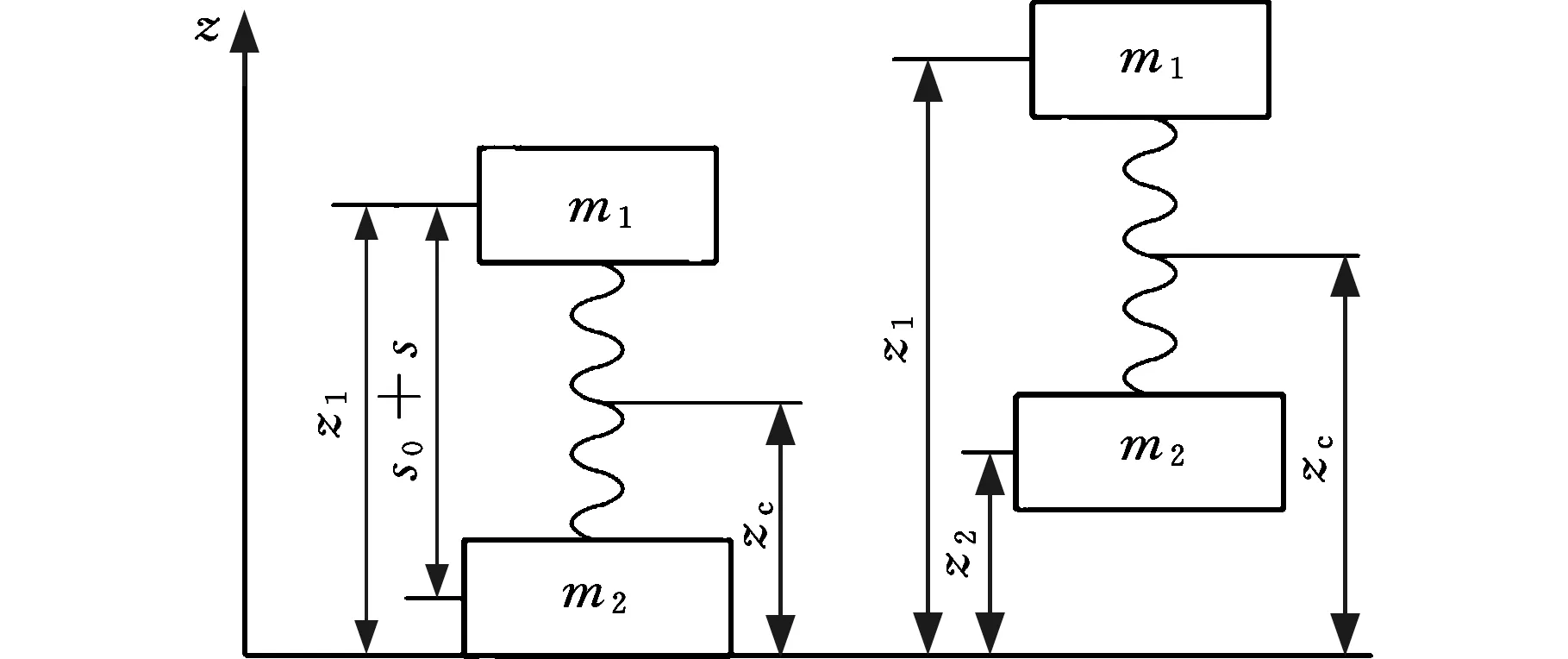
图8 质量-弹簧物理模型

由图8所示的几何关系可知，z1-z2=s0+s，则

(4)

在机器人未离开地面时，对下质量块进行受力分析可得

ks+N-m2g=0

(5)

式中，N为地面支持力。

对整个机构而言，根据质心运动定理，可得

(6)

联立式(4)～式(6)可得

(7)

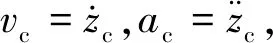
(8)

进而可得

(9)

式中，C1为常数。

由式(9)可知，以质心速度vc为横坐标，质心加速度ac为纵坐标的函数图像为一椭圆曲线。在系统离开地面的瞬间，其质心加速度ac=-g。假设二者交点的横坐标可表示为vc=±vc0，则

(10)

由式(9)可知，当vc=0时，ac=acmax。此时，弹簧的拉伸变形量s也达到最大值。代入式(10)可得最大加速度为

(11)

当系统即将离开地面时，下质量块的加速度为零，对系统利用质心运动定理、对上质量块利用牛顿第二定律，可得

(12)

将式(11)代入式(12)可得，当系统质心的加速度最大时，弹簧的变形量为

(13)

由于当系统刚离开地面时，质心速度vc0>0，所以弹簧的变形量s满足：

(14)

若Emin表示机器人离开地面时弹簧需要释放的最少弹性势能，则机器人的起跳条件为

(15)

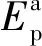
(16)

2.3 非圆齿轮设计

2.3.1弹性势能与齿轮转动参数的关系

在非圆齿轮增速传动阶段，机器人储存的能量转换为上质量块m1的起跳动能，则

(17)

式中，vm1为上质量块的运动速度。

由图3可知，与齿条相啮合的圆齿轮和主体支架的运动状态相同,因此，圆齿轮的线速度与质量块m1的速度相等,又知该圆齿轮与非圆齿轮从动轮共轴线，因此，由齿轮啮合原理可得

(18)

式中，d为圆齿轮的分度圆直径；ω2为非圆齿轮从动轮的角速度。

由式(17)和式(18)可知，非圆齿轮从动轮转动的角速度ω2与弹簧在任意时刻的弹性势能E的关系可表示为

(19)

2.3.2非圆齿轮传动的数学模型

令r1和r2分别表示主从动非圆齿轮的节曲线向径，θ1和θ2分别表示主从动非圆齿轮的转角，a为中心距，i12为齿轮传动比，由文献[22]可知，主动非圆齿轮的节曲线方程可表示为

(20)

从动非圆齿轮的节曲线方程可表示为

(21)

为了方便区分，分别用上标a、b、c表示非圆齿轮增速、等速和减速传动段的各个参数。由图7可知，当非圆齿轮增速传动时(0≤θ1≤θ11)，弹簧的弹性势能随着弹簧的伸缩不断变化，其变化曲线可以用多项式表示为转角θ1的函数：

(22)

式中，a0、a1、a2、a3为多项式系数。

同理，对于等速传动段(θ11≤θ1≤θ13)和减速传动段(θ13≤θ1≤θ14)，随着弹簧的伸缩，其弹性势能变换曲线可分别用多项式表示为

(23)

(24)

式中，b0、b1、b2、c0、c1、c2、c3为多项式系数。

如果给定两非圆齿轮传动的中心距a、主动非圆齿轮转动的角速度ω1和转角θ11、θ12、θ13、θ14的值，只要能够确定式(22)～式(24)中多项式系数的值，并将其代入式(19)～式(21)中，即可得到非圆齿轮的节曲线方程。

上述多项式方程的系数通过各阶段约束方程组求解。由图7可知，弹簧弹性势能与非圆齿轮转角间的运动曲线在增速传动段满足如下约束方程：

(25)

在等速传动段满足如下约束方程：

(26)

式中，n为系数，为了方便计算，本文取n=-0.5。

同理，在减速传动段满足如下约束方程：

(27)

由齿轮啮合原理可知，非圆齿轮主从动齿轮的转动周期相同。因此，当主动齿轮旋转一个周期时，从动齿轮也应正好旋转一个周期，即非圆齿轮在增速传动段、等速传动段和减速传动段的转角之和等于2π，即

(28)

将式(22)～式(24)代入上述约束方程，利用MATLAB软件可获得非圆齿轮的节曲线。

2.3.3参数选取

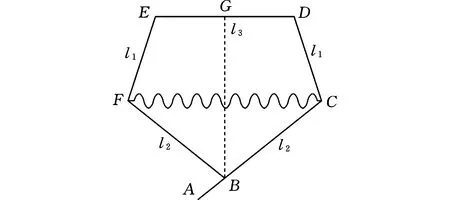
图9 弹跳机构简图

非圆齿轮各传动阶段的转角与跳跃机器人的结构有直接关系，因此本节主要讨论转角θ11、θ12、θ13、θ14的选取。在图9所示的弹跳机构简图中，假定杆EF和CD的长度均为l1，杆BC和BF的长度均为l2，杆DE的长度为l3，G为杆DE的中点，CF连接着弹簧。由跳跃机器人的几何关系可知，与齿条相啮合的圆齿轮在齿条上的位移等于主体支架在起跳阶段的位移ΔlBG，因此

(29)

由图9可知：

ΔlBG=lBG-l′BG

(30)

其中，lBG和l′BG分别为弹簧处于原长和弹簧伸缩时BG的长度，可表示为

根据式(29)和式(30)，只要给定杆长l1、l2、l3、弹簧原长s0和变形量s，即可计算得到转角θ11的值。

齿轮的一个转动周期为2π，即θ14=2π。为方便设计，令非圆齿轮在增速运行段和在减速运行段的转角值相等，即

2π-θ13=θ11

(31)

根据弹跳运动流程，非圆齿轮做等速传动时，机器人已经离开地面进入空中飞行阶段，此时，弹簧处于自由伸缩状态，转角θ12并不影响非圆齿轮增速和减速传动段的节曲线形状，因此，假定

(32)

2.3.4设计流程

如图10所示，非圆齿轮设计流程如下：

(1)给定弹簧初始参数(原长s0、刚度系数k、最大变形量smax等)以及跳跃机器人结构参数(杆长l1、l2、l3、质量m1和m2、圆齿轮分度圆直径等)。

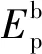
(4)利用MATLAB软件，通过求解式(25)～式(28)可分别得到增速、等速以及减速传动段的多项式系数，将上述系数代入式(22)～式(24)可获得上述各运动段的弹性势能表达式；将上述弹性势能表达式代入式(19)可得非圆齿轮从动轮角速度ω2的表达式，利用i12=ω1/ω2可推导出非圆齿轮传动的传动比；最后根据式(20)和式(21)即可推导出节曲线方程，进而建立非圆齿轮传动的数学模型。

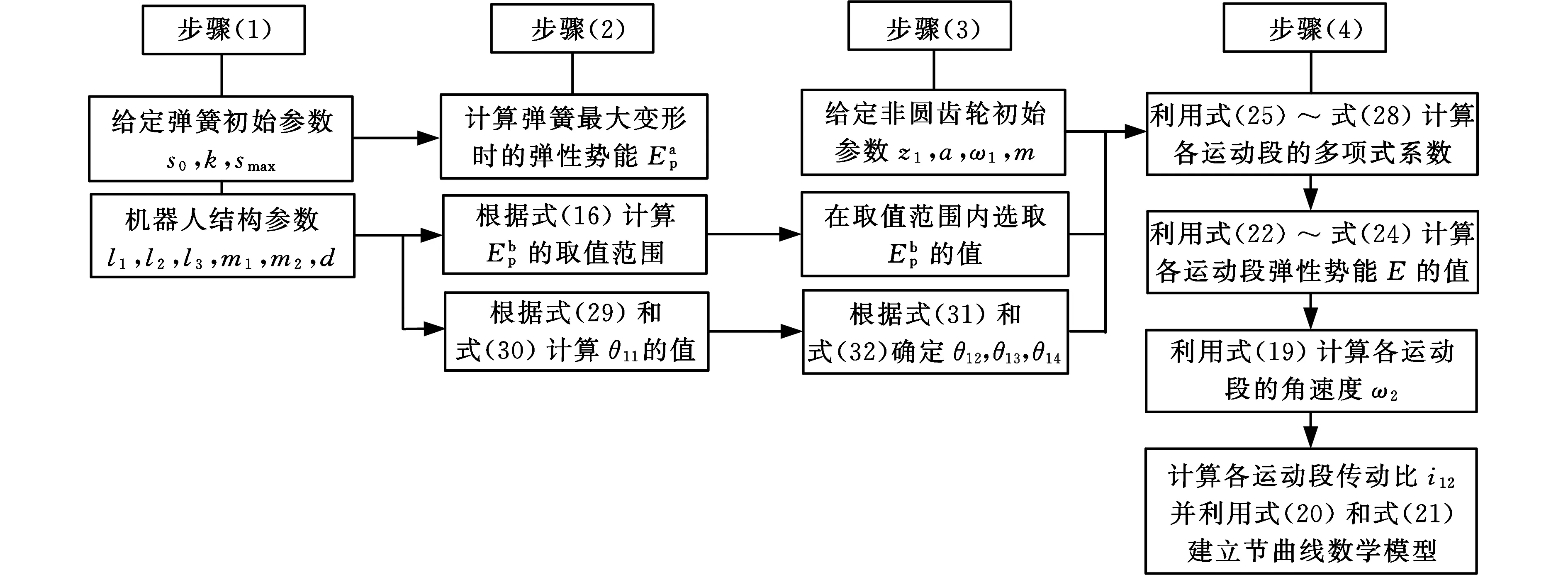
图10 非圆齿轮设计流程图

2.3.5设计实例

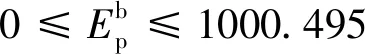
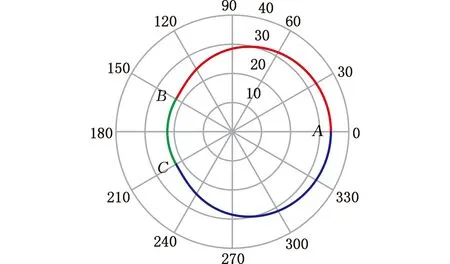
图11 第一组主动齿轮节曲线

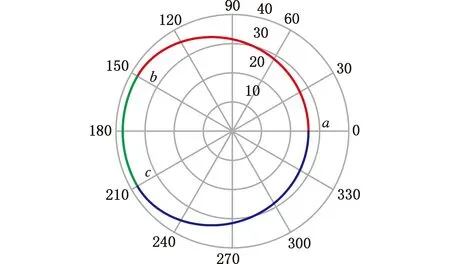
图12 第一组从动齿轮节曲线

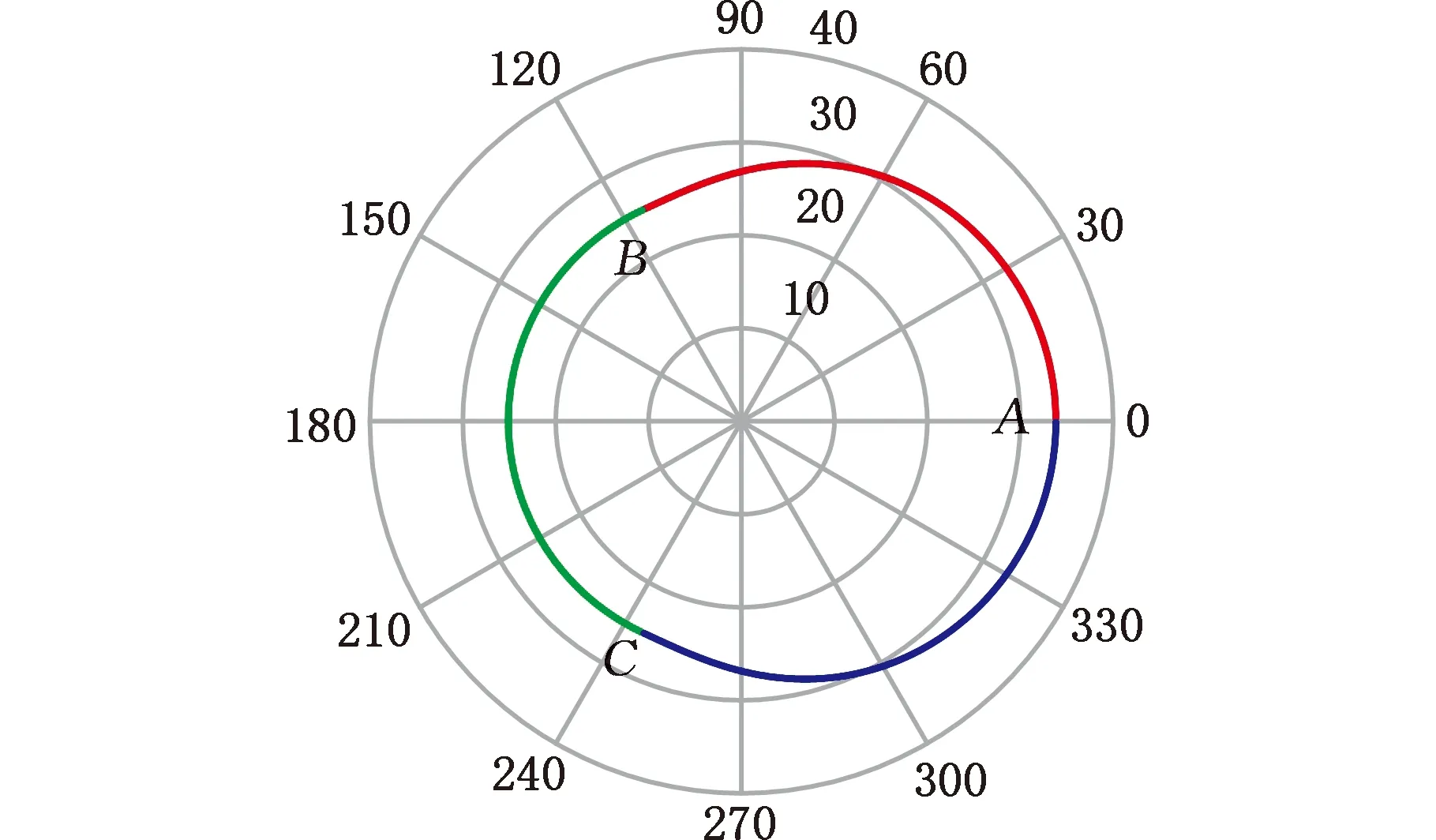
图13 第二组主动齿轮节曲线

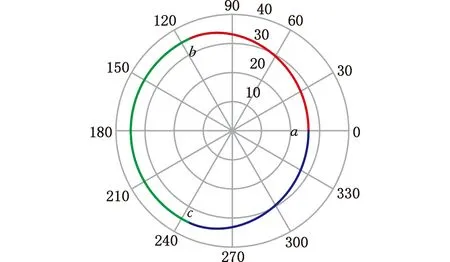
图14 第二组从动齿轮节曲线

3 样机试制与试验测试

为研究跳跃机器人的弹跳性能并验证机构设计的可行性，对机器人进行了样机试制和试验测试。这里主要分析和研究两组不同非圆齿轮对跳跃机器人性能的影响，并将实际测得的能量转换效率与理论值进行对比。机器人中的非圆齿轮采用高精度光敏树脂材料，脚部采用强度好、硬度高但密度相对较大的PLA材料，主体支架、转向盘、圆齿轮等其余零部件采用密度较小但抗冲击能力较强的ABS材料进行3D打印而成。试制完成的跳跃机器人原理样机模型如图15所示。机器人电机为JGB37-545直流减速电机，配备相应的调速器模块，可实现电机正反转和调速功能。姿态传感器BWT61CL配备相应的上位机软件，可实现机构角度、角速度和加速度等参数的测量。激光测距传感器可实现机器人水平和竖直位移的测量。

图15 跳跃机器人原理样机

分别将实例中的两组非圆齿轮安装于跳跃机器人上进行试验测试。测试之前，通过舵机使转向齿轮轴旋转，带动转向齿轮与转向盘啮合，从而调整跳跃机器人脚部与地面之间的夹角大小。经姿态调整试验测得该机器人的最小起跳角度约为55°，最大起跳角度为90°。本试验选择起跳角度为60°，图16为试验测试视频截图。

(a)开始弹跳瞬间 (b)机器人腾空

(c)机器人到达最高处 (d)机器人着陆图16 试验测试视频截图

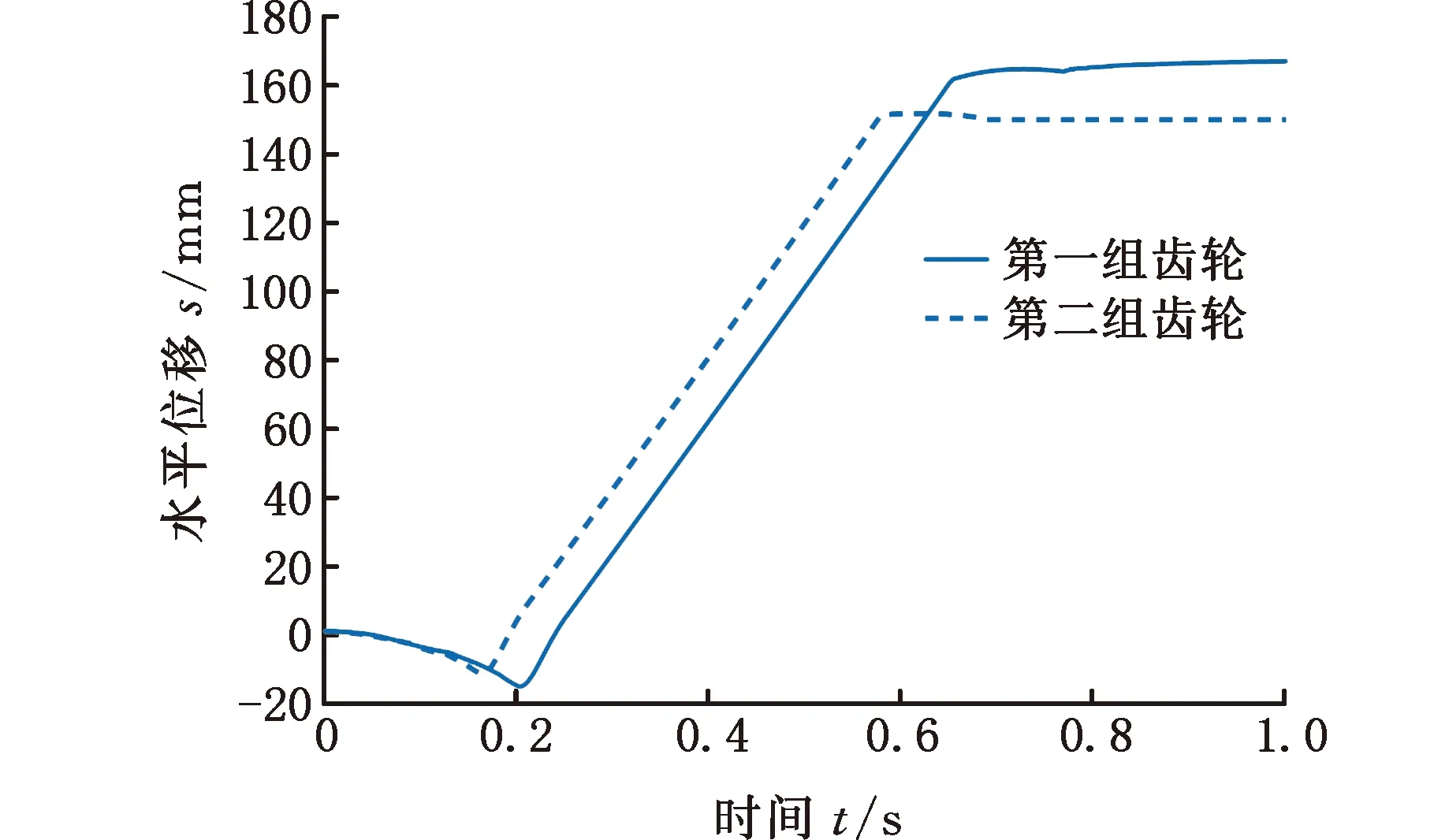
图17 两组齿轮下机器人水平位移对比

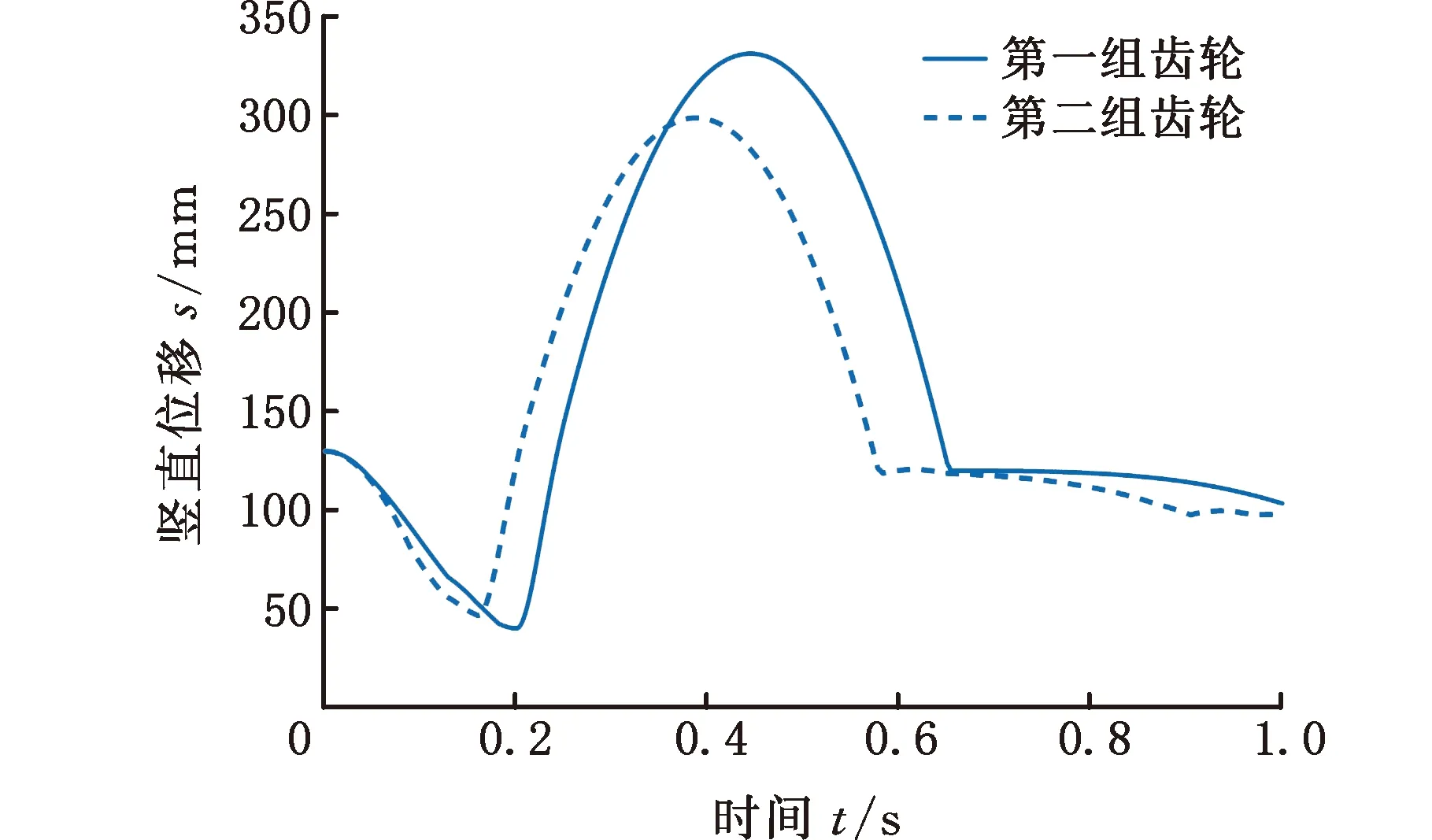
图18 两组齿轮下机器人竖直位移对比

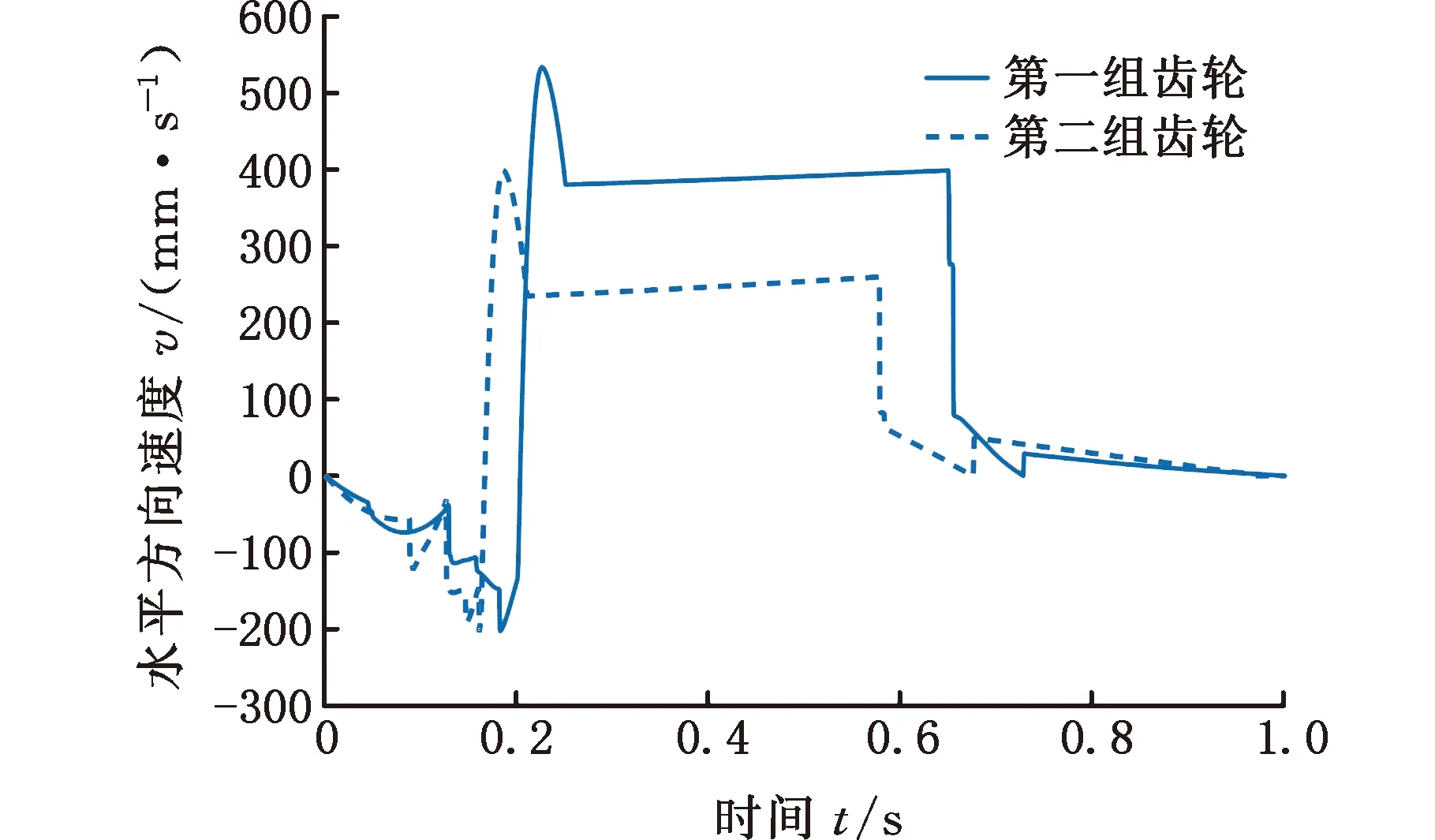
图19 两组齿轮下机器人水平速度对比

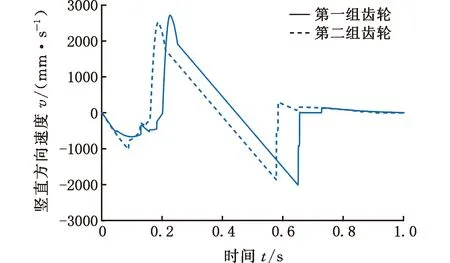
图20 两组齿轮下机器人竖直速度对比

针对实例中的两组非圆齿轮，机器人的水平/竖直位移、水平/竖直速度均可由传感器测得，试验对比数据如图17～图20所示。由图可知，两组非圆齿轮下机器人跳跃的最大水平位移分别为167.04 mm和150.03 mm，最大竖直位移分别为331.08 mm和298.54 mm，其水平方向的最大跳跃速度分别为0.53 m/s和0.39 m/s，竖直方向的最大跳跃速度分别为2.72 m/s和2.53 m/s，机器人离地时刻的瞬时速度分别为2.77 m/s和2.56 m/s。利用上述数据可以计算出机器人离地时动能与弹性势能的值，进而可以得到两组非圆齿轮下的机器人的能量转换效率分别为75.8%和64.7%，与给定的理论值相比，误差分别为4.05%和6.37%，均在许可范围内。

4 结论

(1)完成了跳跃机器人的基本结构设计。利用弹簧和齿轮齿条等机构建立了跳跃机器人能量转换的设计和实现方案，利用转向齿轮和尾杆机构开展了姿态调整机构的设计，可实现x方向的姿态调整。

(2)建立了机器人能量转换的主动控制方案。利用齿轮啮合理论分别建立了非圆齿轮增速、等速和减速传动段与机器人弹跳、空中飞行和着陆阶段的映射关系，推导了机器人的起跳判据。在此基础上，以能量转换曲线研究非圆齿轮节曲线，以非圆齿轮共轭啮合特性研究跳跃机器人的能量转换特性，建立了非圆齿轮传动的数学模型，实现了通过改变能量转换曲线中的关键参数主动控制机器人能量转换效率。

(3)完成了机器人样机试制和试验测试。使用3D 打印技术制作了物理样机，并利用两组非圆齿轮开展了对比试验，结果表明：机器人可以实现稳定跳跃，且两组非圆齿轮下的机器人能量转换效率的测量值与理论值的误差均在许可范围内，验证了本文设计方法的正确性和合理性。

新型跳跃机器人的运动学和动力学仿真及分析、结构优化设计、连续性跳跃性能试验等内容将另文讨论。