负弯矩作用下含角钢连接件的叠合板组合梁力学性能研究
2023-01-05丁克伟张星辰刘运林贾高宗房尚京
丁克伟, 张星辰, 刘运林, 贾高宗, 房尚京
(安徽建筑大学 土木工程学院,安徽 合肥 230601)
钢-混凝土叠合板组合梁是组合梁中的一类,近年来在装配式建筑领域得到广泛应用。叠合板组合梁不仅具有现浇组合梁的优势,还具有施工速度快、节省支模工序与材料的优势。对于现浇钢-混凝土组合梁在负弯矩作用下的力学效应,相关研究成果较丰富。文献[1-3]研究负弯矩作用下滑移影响的附加挠度对于整体构件刚度的影响,并提出钢-混凝土组合梁折减刚度计算公式;文献[4-6]研究含聚乙烯醇(polyvinyl alcohol,PVA)纤维与水泥基体复合材料(engineered cementitious composite,ECC)的混凝土组合梁在负弯矩作用下的力学性能,提出了含ECC的混凝土组合梁受弯裂缝宽度计算公式;文献[7-10]研究腹板开孔类的组合梁在负弯矩作用下的抗剪性能,提出剪力连接件的拔出力公式;文献[11-12]研究负弯矩作用下钢-混凝土蜂窝组合梁的力学性能,发现改变腹板高厚比与翼缘宽厚比对构件承载力有明显影响。
叠合板拼缝处设置的附加钢筋能有效抑制拼缝的开展,提高叠合板极限承载力。文献[13-15]提出一种多功能限位器,使拼缝处的钢筋形成桁架形式,提高受力性能,试验结果表明新型拼缝结构等同于现浇,多功能限位器提高了传力性能和施工效率。
由于预制叠合底板伸出“胡子筋”构造的模具需要开孔,不同的预制底板需要不同的规格,施工中还需要现场穿筋,且要避免与钢梁上栓钉发生冲突,最终导致浇筑模具成本增加。文献[16]设计5块预制底板不出筋的密拼单向叠合板,对其进行两点静力加载试验,并提出2种新型拼缝构造,避免了拼缝处裂缝沿叠合面横向发展而过早破坏;文献[17]对角钢抗剪连接件进行推出试验研究,提出角钢连接件的地基梁模型;文献[18]研究分离式叠合板组合梁在正弯矩作用下的受力性能,发现拼缝的存在削弱了试件的抗剪承载力。
为了避免叠合板出筋所造成的问题,本文设计一种含角钢连接件的叠合板组合梁,在角钢的一面焊接伸进预制叠合底板的钢筋,将角钢另一面焊接在钢梁上;对这种密拼型钢筋桁架叠合板组合梁进行负弯矩单点静力试验及有限元模拟。
1 试验概况
1.1 试验设计
试验以预制叠合底板是否带角钢连接件为参数,设计2根简支叠合板组合梁。试件参数见表1所列,具体试件尺寸如图1所示(单位为mm)。

表1 试件参数信息
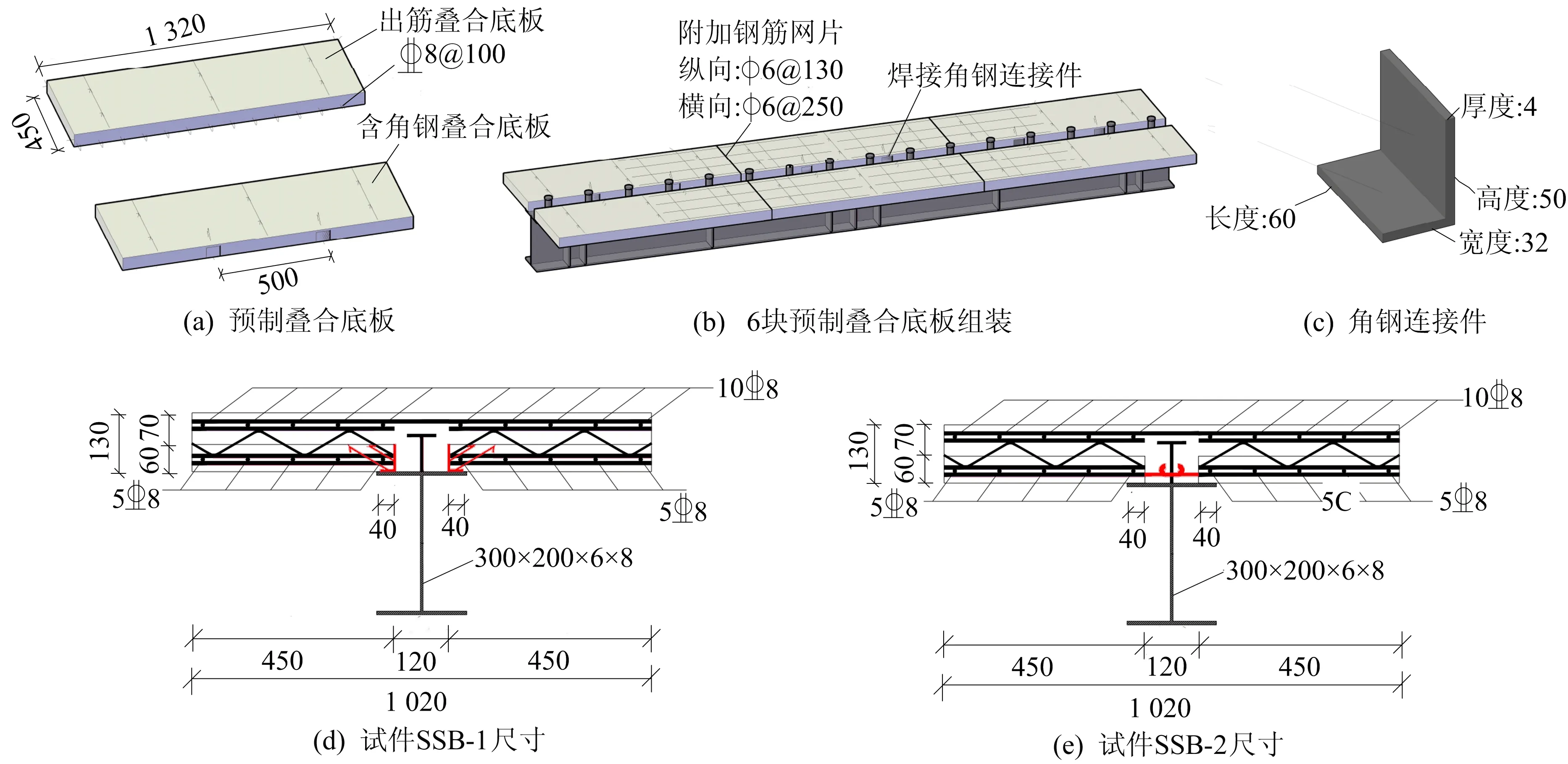
图1 试件尺寸
钢梁采用Q235B热轧H型钢,钢梁两边焊接加劲肋,栓钉规格采用M16-100。按文献[19]中公式进行完全抗剪设计,布置栓钉数量为14个,栓钉间距为250 mm。
抗剪设计具体计算公式为:
Vs=Astfst
(1)
(2)
nf=Vs/Vu
(3)
η=n/nf
(4)
其中:Vs为钢梁与混凝土交界面的纵向剪力;Ast为钢筋截面面积;fst为钢筋受拉受压强度设计值;Vu为栓钉的抗剪承载力;Asd为栓钉截面面积;Ec为混凝土弹性模量;fc为混凝土轴心抗压强度设计值;fus为栓钉的极限抗拉强度设计值;nf为组合梁完全抗剪时所需栓钉数量计算值;n为组合梁中实际栓钉数量;η为栓钉剪力连接度。
1.2 材料性能
混凝土叠合底板与后浇混凝土板均采用C30混凝土,参照文献[20]对混凝土试块进行抗压强度试验,最终得到叠合底板混凝土立方体抗压强度为35.6 MPa,后浇层混凝土立方体抗压强度为33.2 MPa。按照文献[21]的要求,截取试件制作时同批次钢筋及钢梁母材进行材料性能试验,试验结果见表2所列。

表2 钢材力学性能试验结果
1.3 加载装置与加载方案
试验在安徽省建筑结构与地下工程重点实验室进行。加载装置示意如图2所示,试验前期将叠合板组合梁倒置,在钢梁中心位置放置加载钢板、500 kN液压千斤顶、压力传感器,并与反力架正中心在一条水平线上,保证竖向荷载与组合梁重心处于同一垂直平面内。
动物模型建立 采用40%四氯化碳溶液腹腔注射法构建大鼠病毒性肝纤维化模型,剂量为3 μl/g体重,每周2次,分别注射4周(实验组1)、8周(实验组2)、12周(实验组3),以制备不同程度的肝纤维化模型。对照组腹腔注射等量的生理盐水。
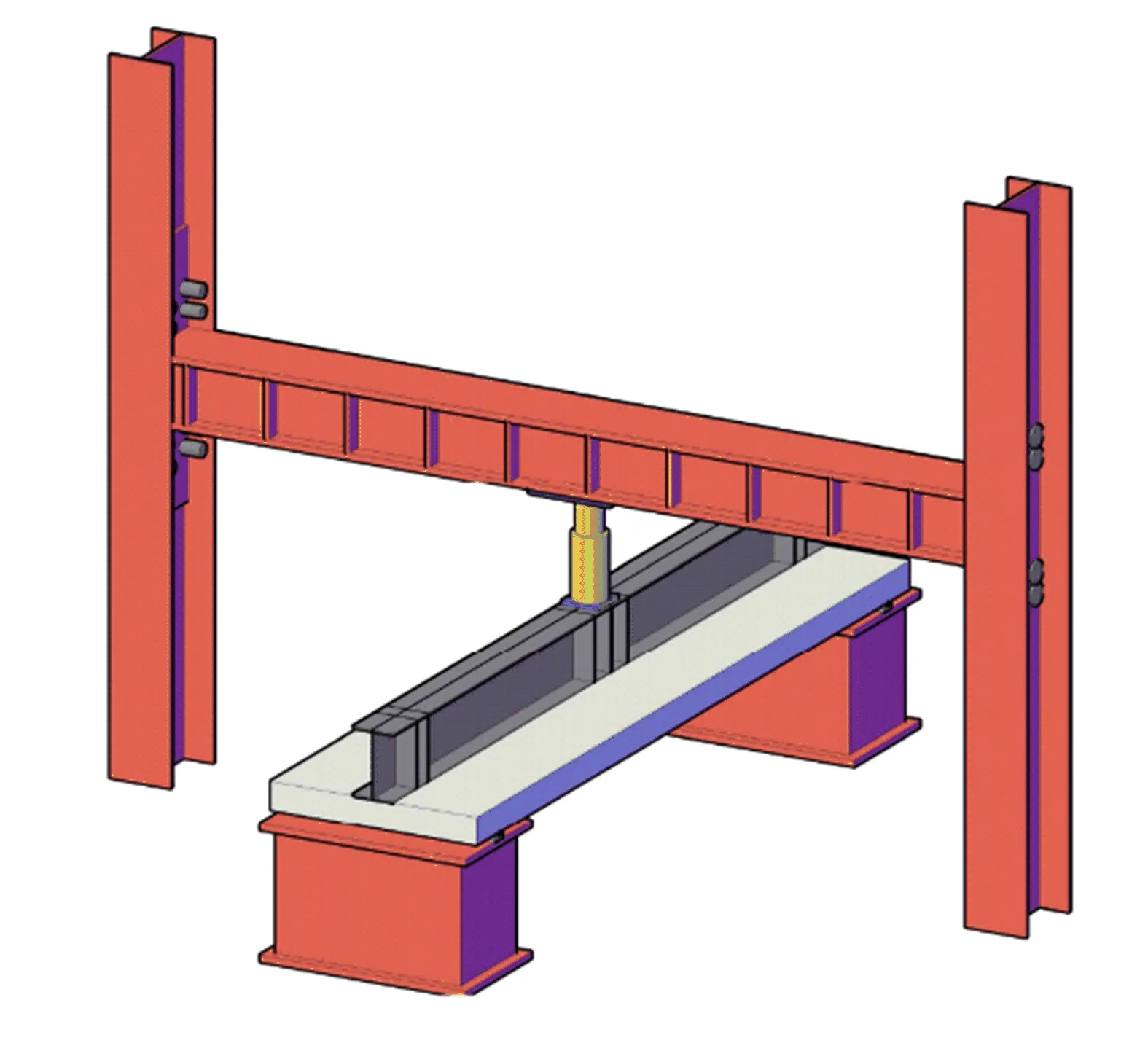
图2 加载装置示意
加载制度采用力控制加载;在正式加载前先进行预加载,以每级15 kN加载至30 kN,然后卸载至1 kN;正式加载以每级15 kN加载至150 kN,然后以每级30 kN加载至试件破坏。
2 试验现象与结果分析
试验加载现场图片如图3所示,叠合板板底裂缝分布如图4所示。

图3 试验加载现场图片
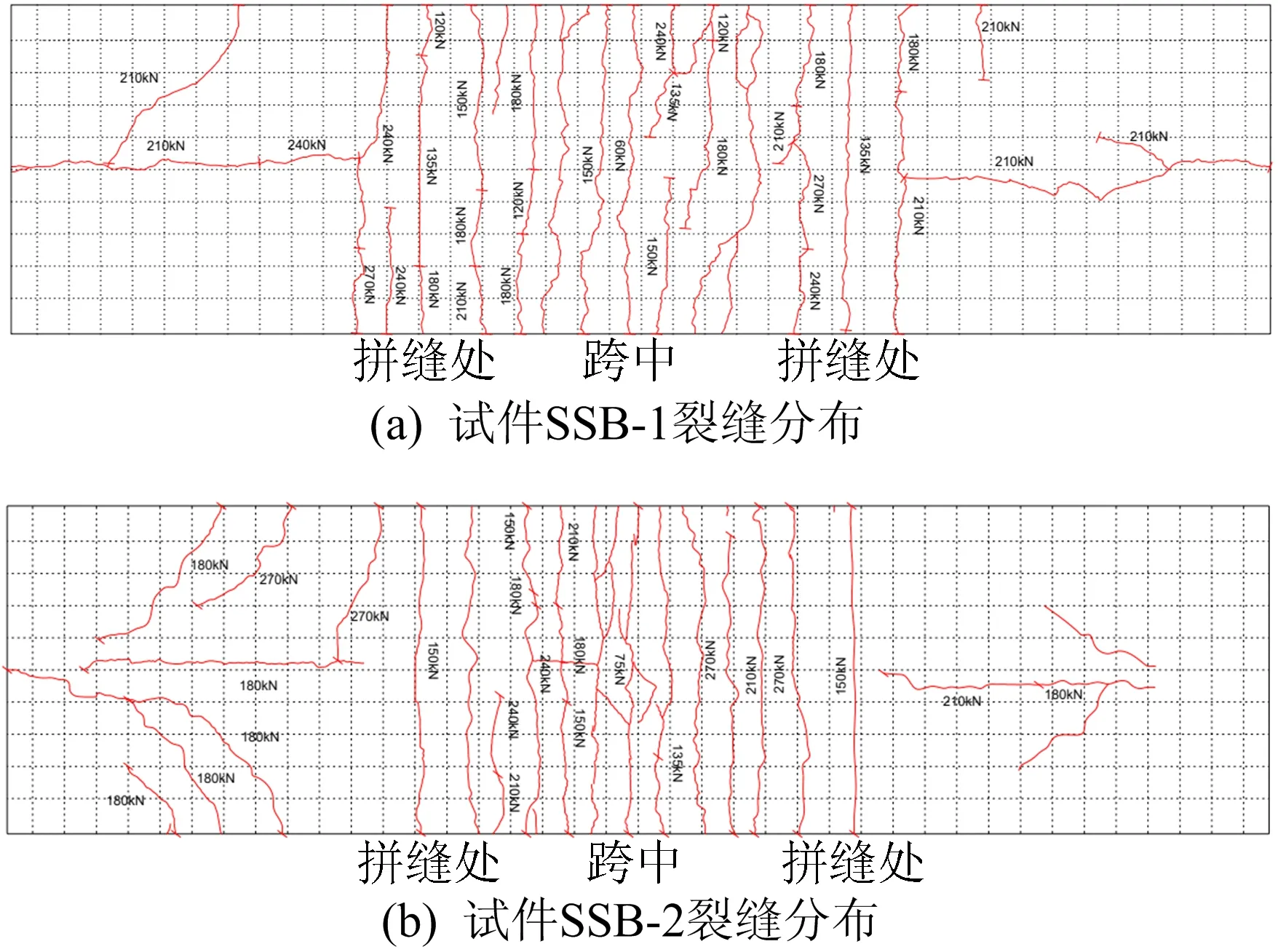
图4 试件板底裂缝分布情形
对于试件SSB-1,荷载分别加载至60~75 kN、120~135 kN、210~240 kN时,叠合板板底接连出现跨中横向受拉裂缝、拼缝处横向受拉裂缝、纵向剪切裂缝。对于试件SSB-2,上述3种裂缝分别出现在75~90 kN、120~135 kN、180~210 kN。荷载加载至270~300 kN时,2个试件均出现钢梁翼缘、腹板屈曲现象;加载至296 kN左右时,2个试件承载力下降,最终均表现为受弯破坏。
从图4可以看出,试件SSB-2裂缝密度大于试件SSB-1,即试件SSB-2裂缝的间距小于试件SSB-1的裂缝间距。混凝土翼缘板受拉破坏是由于抗剪连接件传递剪切力,在混凝土中产生拉应力所导致的,试件SSB-1抗剪连接件的数量多于试件SSB-2,从而影响了裂缝间距。
2个试件主要试验结果见表3所列。表3中:Pcr为开裂荷载;Py为屈服荷载;Pu为组合梁承载力下降时的极限荷载;δcr、δy、δu为与荷载相对应的挠度。2个试件屈曲破坏时Pu相近,试件SSB-1的Pcr小于试件SSB-2,但其Py大于试件SSB-2。
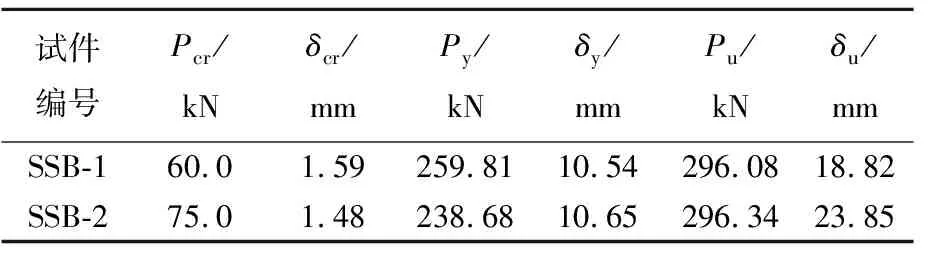
表3 2个试件主要试验结果
2个试件的荷载-相对滑移曲线如图5所示。
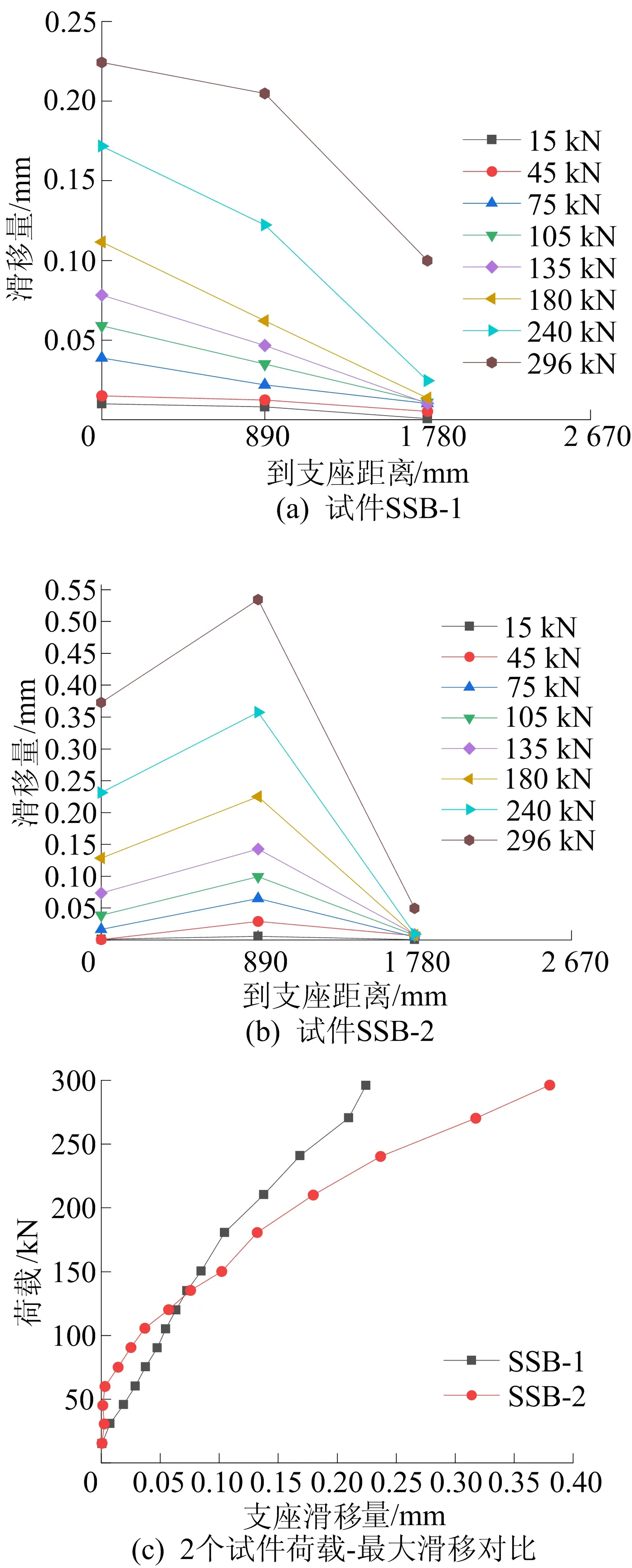
图5 2个试件的荷载-滑移曲线
从图5可以看出:试件SSB-1初期弹性阶段时沿组合梁跨度方向各处的滑移呈线性增长,且符合弹性阶段组合梁支座处滑移最大、跨中滑移最小的规律[1];由于出筋构造使得叠合板整体性能更好,导致当荷载水平较低时,试件SSB-2支座处滑移并未出现增长,且1/4净跨处滑移量大于支座处;随着荷载增加,试件SSB-2整体滑移量大于试件SSB-1,这是由于角钢连接件作为抗剪连接件起到减小滑移量的作用,从而使得试件的附加挠度变小。
2个试件荷载-跨中挠度曲线如图6所示,跨中截面沿高度方向的应变分布如图7所示。

图6 2个试件的荷载-跨中挠度曲线

图7 2个试件的跨中应变沿截面高度分布
由图6可知:在加载初期,2个试件的荷载-挠度曲线呈线性关系且几乎一致;在混凝土开裂后,试件SSB-1的挠度增长速率小于试件SSB-2。根据负弯矩折减刚度计算公式[2],因为角钢连接件可减小附加挠度,减小折减刚度系数,所以试件SSB-1抗弯刚度大于试件SSB-2。
从图7可以看出,截面应变沿高度方向呈非线性分布,呈抛物线变化,平截面假定无法成立。其主要原因如下:① 跨中混凝土板与钢梁的交界面处滑移最小,但滑移应变最大,使得交界面处产生应变突变,试件SSB-2的应变突变非常明显;② 由于叠合板中存在剪力滞的影响,造成混凝土板的纵向拉应变在板的横截面上分布不均匀,以至于距叠合板中心位置越远,混凝土所受拉应变越小。
从图7还可以看出,在混凝土开裂前,试件SSB-2的叠合板纵向拉应变小于试件SSB-1。钢梁与混凝土之间的自由滑动可以释放混凝土的受拉应力,降低混凝土开裂风险。角钢连接件可以减小混凝土与钢梁之间的相对滑移,限制了两者的自由滑动,最终导致试件SSB-1的混凝土先于试件SSB-2开裂。
3 弹性抗弯刚度计算
试件SSB-1、SSB-2极限弹性状态均由钢梁翼缘屈服控制,其弯矩Meu的计算公式[1]为:
Meu=
(5)
其中:As为钢梁截面面积;Is为钢梁自身的截面惯性矩;Ws为钢梁截面抵抗矩;h为钢梁高度;y0=yr+ys,yr、ys分别为钢筋、钢梁形心到混凝土板与钢梁交界面的距离。
本文弹性抗弯刚度计算采用文献[2]中负弯矩区钢-混凝土组合梁折减刚度表达式,只考虑钢梁与混凝土板之间相对滑移的影响以及钢筋与混凝土板之间黏结滑移效应的影响,不考虑混凝土板对刚度的贡献及角钢连接件对滑移的影响,则计算公式适用于试件SSB-2。
2个试件挠度、刚度计算结果见表4所列。表4中:P为极限弹性承载力;δ1为试件的跨中挠度试验值;δ2为试件SSB-2未考虑滑移的跨中挠度计算值;Δδ为附加挠度;δ3为试件SSB-2考虑滑移后跨中挠度计算值;(EI)1为试验刚度;(EI)2为计算刚度。
考虑滑移后试件SSB-2的跨中挠度及抗弯刚度计算值与试验值吻合度良好,验证了理论计算符合实际情况,故可通过试件SSB-2的计算值与试件SSB-1的试验值相对比。由表4可知,混凝土板开裂后试件SSB-1的抗弯刚度相对于试件SSB-2提高23%。因此,在叠合底板中预埋角钢连接件对试件的抗弯刚度增加有显著作用。

表4 试件挠度、刚度计算结果对比
本文引入真实剪力连接度概念。当纵向钢梁上有角钢与栓钉2种抗剪连接件时,两者将共同分担纵向剪力,则栓钉所承担的剪力将小于实际纵向剪力。按照文献[19]计算组合梁完全抗剪时,所需完全抗剪的栓钉数量降低,从而使得真实剪力连接度小于计算的栓钉剪力连接度。若组合梁内部只含栓钉抗剪连接件,则真实剪力连接度等于计算值。因此,试件SSB-1计算值小于表1中真实值,试件SSB-2计算值等于表1中真实值。
4 有限元模拟与分析
采用ABAQUS软件对试件SSB-1进行有限元模拟,并与试验组进行对比。考虑到角钢连接件在组合梁中承担混凝土与钢梁界面的部分纵向剪力,为研究角钢连接件抗剪性能的强弱,通过减小真实剪力连接度,对不出筋含角钢连接件的叠合板组合梁进行参数化分析,具体组合梁参数见表5所列。

表5 有限元模拟试件参数信息
试件荷载-跨中挠度曲线有限元模拟与试验结果对比如图8所示。
从图8a可以看出,有限元结果与试验结果几乎吻合,证明了模型的合理性。
从图8b可以看出,当栓钉的剪力连接度从1.06降低到0.69时,试件SSB-5相对于试件SSB-3从完全抗剪降为部分抗剪时,抗弯刚度发生降低,但试件SSB-4相对于试件SSB-1的抗弯刚度并未发生太大变化。
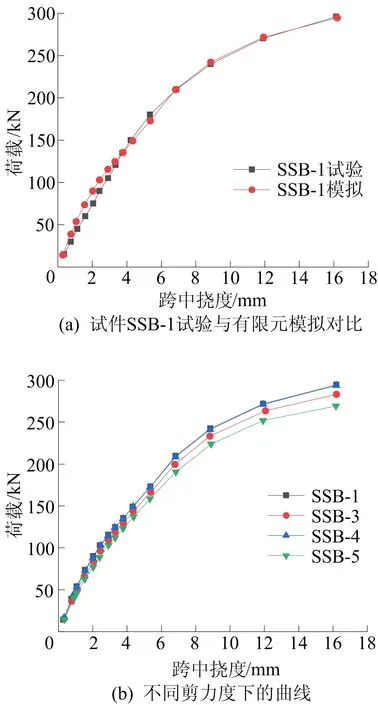
图8 试件荷载-跨中挠度曲线有限元模拟与试验结果对比
文献[22]研究发现,抗弯刚度随着剪力连接度的增大而增大,当剪力连接度超过2时,剪力连接度对抗弯刚度的影响不明显。本文中试件SSB-1、SSB-4的真实剪力连接度均超过2,验证了角钢连接件使栓钉剪力连接度的计算值小于真实值。
有限元模拟下不同剪力连接度叠合板组合梁的屈服特征值及抗弯刚度见表6所列。试件SSB-3、SSB-4相对于试件SSB-5的抗弯刚度分别增加6%、12%,由此可知,叠合底板中预埋角钢连接件对试件刚度的提升效果更显著。

表6 不同剪力连接度试件的屈服特征值及刚度
5 结 论
本文对组合梁进行单点静力加载试验,在试验基础上,对不同剪力连接度的组合梁进行数值模拟对比,得出以下结论:
(1)相对于出筋叠合底板,在叠合底板中加入角钢连接件会增大混凝土板横向开裂风险、减小纵向开裂风险,对试件的极限承载力影响不大。
(2)将负弯矩区钢-混凝土组合梁折减刚度公式得到的计算值与试验值进行对比,结果验证了在叠合底板中预埋角钢连接件可以提高组合梁的抗弯刚度。
(3)有限元模拟结果表明,预埋角钢连接件可以减少完全抗剪所需的栓钉数量,按相关规范计算的栓钉剪力连接度低于真实值。与增加栓钉数量相比,增加一定数量的角钢连接件对叠合板组合梁抗弯刚度的提升效果更加显著。
