基于SSA-SVR模型的城市轨道交通短时进站客流预测
2023-01-04帅春燕谢亚威欧阳鑫
帅春燕,谢亚威,单 君,欧阳鑫
(1. 昆明理工大学交通工程学院,昆明 650500;2. 昆明理工大学信息工程与自动化学院,昆明 650500)
近年来,我国城市轨道交通建设有了快速发展,但是轨道交通的运量经常难以满足客流量的需求,客流分布不均衡、换乘不便等问题亟待解决,轨道交通短时客流预测逐渐成为研究热点,预测精度直接影响轨道交通运营计划和组织方案的制定。熊杰等针对地铁换乘客流量,提出了利用Kalman滤波进行短时客流预测的方法[1]。袁坚等从时空两个维度分析轨道交通客流分布的特点,提出基于贝叶斯网络的客流量预测方法[2]。平滑技术用于更清楚地揭示潜在趋势、季节成分和周期成分[3]。时间序列本身不可避免地包含噪声,对原始时间序列不加处理地直接进行建模和预测会对模型的预测能力产生影响[4]。杨静等提出一种基于变点模型、小波模型、自回归滑动平均模型(ARIMA)的组合模型来对轨道交通短时客流进行预测[5]。朱广宇等基于轨道交通客流变化特点[6],构建自回归求和滑动平均(ARIMA)模型和BP神经网络模型相组合的客流预测模型。赵阳阳等结合深度学习理论,提出一种基于经验模态分解与长短时记忆神经网络的短时地铁客流预测模型[7],降低了地铁客流样本噪声对客流预测模型的干扰。梁强升等考虑城市轨道交通客流的时空交互关系[8],提出一种融合循环门控单元和图卷积神经网络的城市轨道交通客流预测模型(GCGRU)。赵建立等提出一种将卷积神经网络(CNN)与残差网络(ResNet)相结合的预测模型(ResNet-CNN1D)来解决城市轨道交通多站点短时客流量预测问题[9]。Haiying Li等提出一种预测出站客流和改善客流控制的动态径向基函数神经网络[10]。郇宁等提出一种改进KNN算法的地铁进站客流实时预测方法[11]。林涛等针对风速的强非线性特点,提出一种奇异谱分析和改进粒子群优化自适应模糊推理系统的短期风速预测模型[12]。王茜竹等提出一种基于奇异谱分析(SSA)-自回归移动平均(ARIMA)的短时客流预测方法[13],预测公交短时客流。
由于轨道交通进站客流具有规律性、随机性以及噪声等特性,客流特征在不同的时段也会有较大差异。单一模型目前已很难准确获取客流的这些复杂特性,所以客流的短时预测也由单一模型向复合模型转换。当时间间隔较短时,进站客流的规律性可能被随机性掩盖,而直接对原始数据进行预测可能会有较大误差,为了能够准确地获取客流的短时变化特征,进而准确地预测客流,有必要对客流进行主要特征的提取和去噪。笔者结合AFC(自动售检票系统)数据,提出了一种基于SSA分解,针对不同的客流成分采用SVR进行组合预测的SSA-SVR混合模型。实验结果显示,笔者的模型显著提高轨道交通短时客流预测精度和预测稳定性。
1 SSA与SVR模型介绍
1.1 SSA模型
奇异谱分析(SSA)[14]是一种处理非线性时间序列数据的方法,通过对所要研究的时间序列的轨迹矩阵进行分解、重构等操作,提取出时间序列中的不同成分序列(长期趋势、季节趋势、噪声等),从而对时间序列进行分析或去噪。采用SSA对时间序列进行分析并预测时,SSA相当于对原始序列作了低通滤波,滤去了序列中的高频噪声和非周期性的异常现象,从包含噪声的有限长观测序列中提取出主要信息,并依据这些信息建立预测模型,增强了时间序列的可预测性。SSA既不需要假设参数模型,也不需要假设平稳性条件,适用于分析含有潜在结构的非平稳时间序列,目前已广泛应用于水文预测、电力负荷预测和天气预测等方面。笔者将之应用于分解提取出轨道交通客流的特征,算法执行可分为以下4个步骤:
1) 嵌入。选择适当的嵌入维数d,将所观察到的一维时间序列数XT=(x1, …,xT)转化为d维序列Xi=(xi, … ,xi+d–1)T,则由K个向量组成的K列轨迹矩阵,如下式所示:
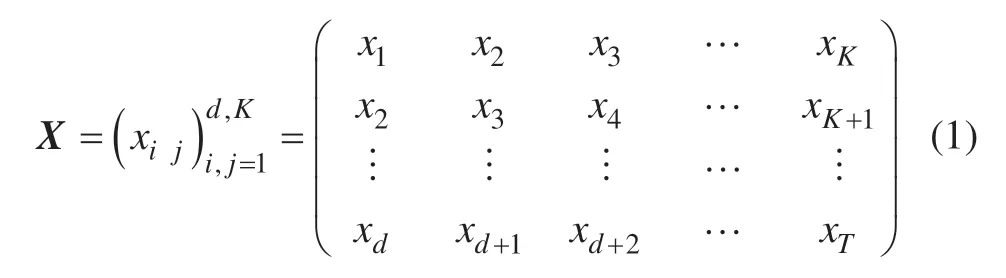
其中嵌入维数d的选择规则为:
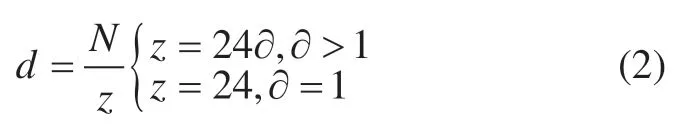
其中,N为样本数量;∂为每小时采样数;z为中间变量。
2) SVD分解。计算协方差XXT求得d个特征值λ1≥λ2≥, …, ≥λd≥0,U1, …,Ud为其所对应的正交特征向量,令则:

式中,X为第i个SVD分量;为矩阵X的奇异值;Ui为矩阵X的经验正交函数;Vi为X的主成分;Ei为基本矩阵。


由上式得到矩阵XIk,生成序列X(k)=则原始序列可分解为m个时间序列的和:
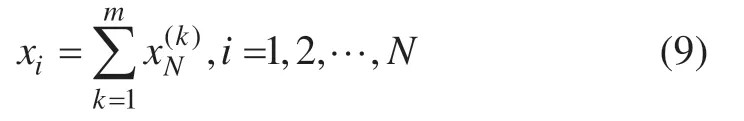
1.2 SVR模型
支持向量机(SVM)使用结构风险最小化原则替代经验风险最小化原则,从理论上保证了模型的最大泛化能力[15]。支持向量机应用到非线性回归估计和曲线拟合中,成为支持向量回归机(SVR)。

通过极小化下式的结构风险系数,使上式的估计真实风险最小:

式中,||w||2描述与模型复杂度相关的因素;C为惩罚系数,C越大则对数据的拟合程度越高;为ε不敏感损失函数,其定义如下:

上述函数回归问题等价于:

并满足以下条件:
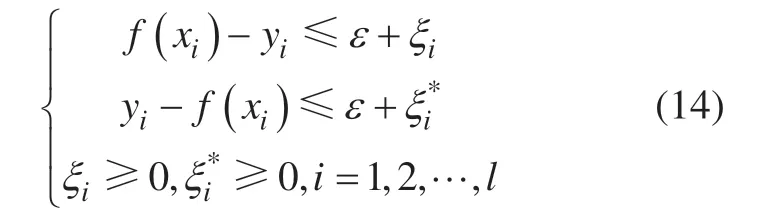
其中ξi、为松弛变量,表示样本偏离ε不敏感区域的程度。
对(14)式,求解模型的Lagrange对偶问题获得原问题的最优解:
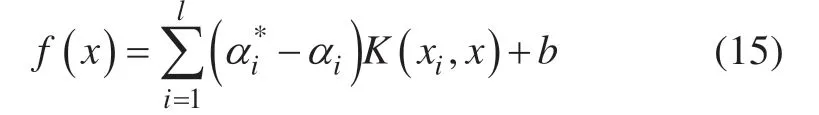
其中,iα、*iα为Lagrange乘子为一个满足Mercer条件的核函数,径向基核函数不仅具有较少的参数,还具有良好的性能,因此,本文采用径向基核函数构造SVM回归机。径向基核函数表达式如下:

本文中,径向基核函数的参数γ和惩罚系数C是SVR模型需要确定的两个参数。
所以,笔者提出SSA-SVR组合预测模型对地铁进站客流进行预测,与现有的地铁进站客流预测最优模型进行对比,从而发现提高预测精度和稳定性的一种新方法。
2 短时客流预测模型构建
2.1 数据来源与分析
选取北京市轨道交通客流2015年11月共19个工作日的数据,按每天06:00—23:00进行时间划分,共计14条线路,268个站点。将站点划分为:大量级为大于2.5×104(人)/d,共72个站点;中量级为1×104~2.5×104(人)/d,共116个站点;小量级为0~1×104(人)/d,共80个站点。在统计各站点日均进站客流量的量级基础上,按从大到小将量级排序,如图1所示。
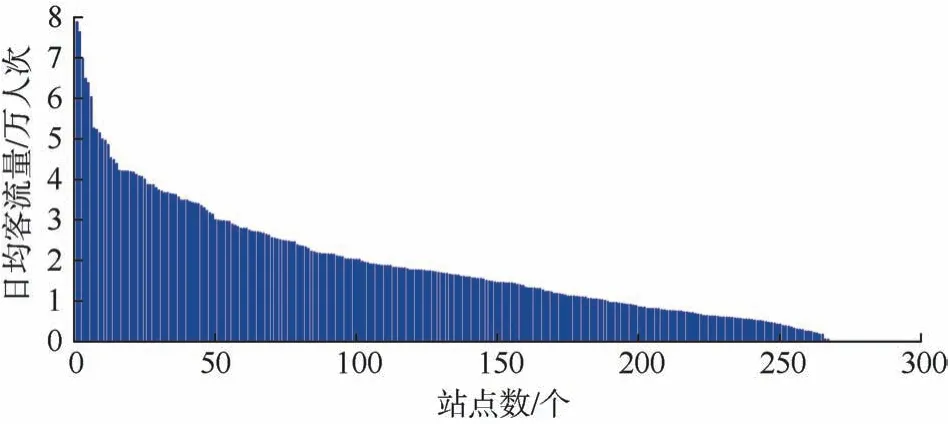
图1 268个站点日均进站客流量分布Figure 1 Daily average passenger flow distribution of 268 stations
按各站点日均客流量量级大小,以15 min为时间间隔,抽取部分站点,取前14天的数据为训练集,后5天的数据为测试集,对站点进站客流预测未来5个工作日的每15min的客流。
在奇异谱分析中,窗口长度d取68,即一天交通客流量序列的长度。原始时间序列通过奇异谱分析,按从大到小进行奇异值的排序,划分为趋势、随机、振荡和噪声4种成分(见图2),笔者采用粒子群算法进行参数寻优,最后根据本数据寻得模型最优参数为前30%特征值为主要重构序列成分,后3种为次要成分按顺序分别取30%、30%和10%。
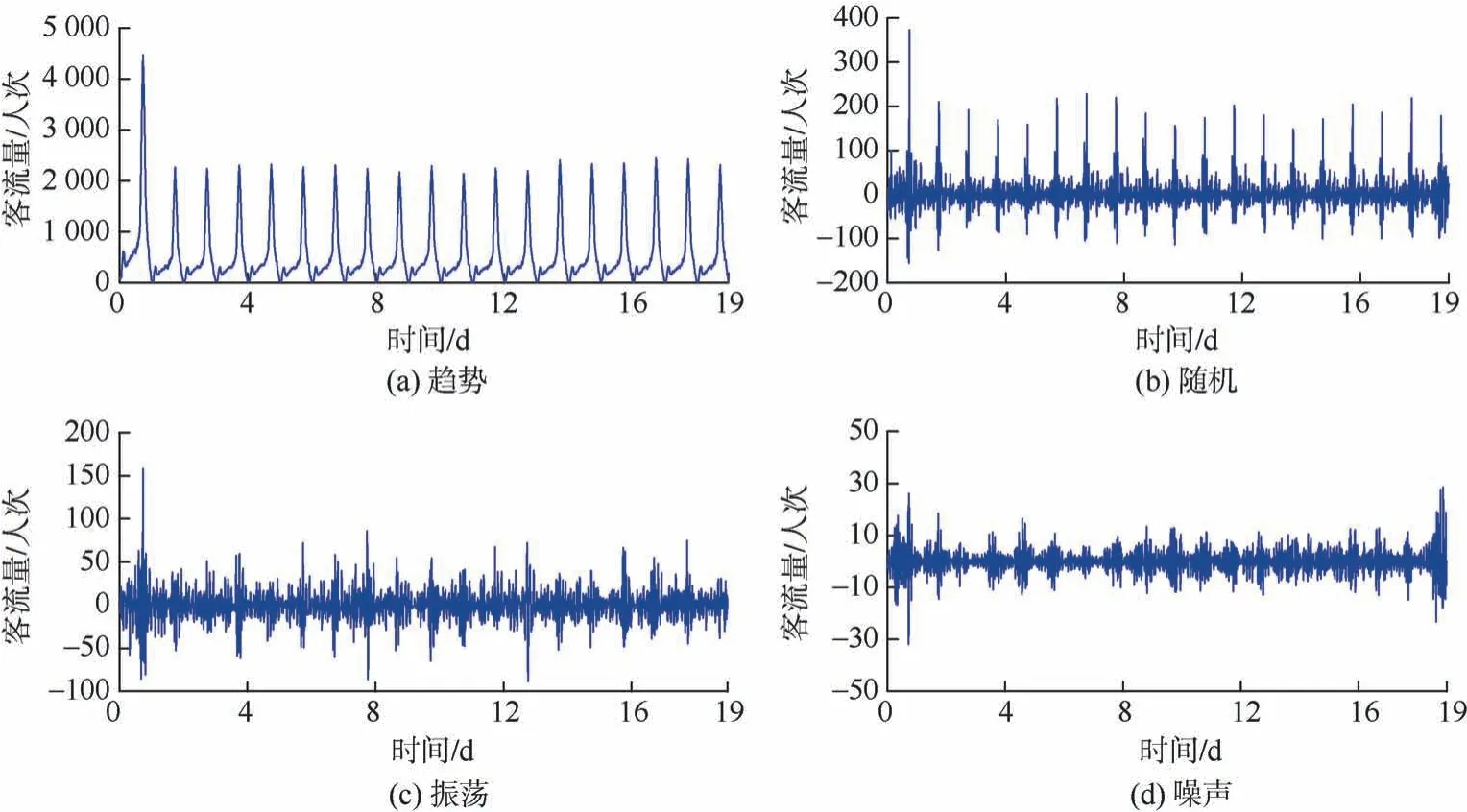
图2 4种重构序列Figure 2 Four types of reconstruction sequences
2.2 模型建立
现有地铁短时客流预测模型中的数据输入分为两类:一是以天(d)为单位,不分时段,将所有历史数据都作为输入;二是将一天分为不同的时段,再把每天的同一时段的客流作为数据的输入。由于地铁客流的特点,以天为单位作为输入,不能精确预测出地铁一天中不同时段的客流量;以每天的某个时段作为数据输入,前后时刻客流的影响难以把握,最终都会影响模型的精度。笔者采取将每天06:00—23:00时间内,按15 min为时间粒度,进行时段划分。模型建立步骤如下:
步骤一:轨道交通客流时段划分。以天为单位对客流进行时段划分,输入数据为划分好的每个时段的客流。
步骤二:奇异谱分析。首先SSA模型对原始时间序列数据进行分析,得到去除噪声的时间序列。具体从①嵌入:确定窗口长度;②分解:获得多个奇异值;③分组:将奇异值按从大到小排序,利用粒子群寻优得到的参数划分奇异值的主要信息成分和次要成分;④重构:根据③的分组,选择前n个主要成分组成新的时间序列,根据实际需求,重构时间序列分为4个部分进行分析。
步骤三:基于SVR模型预测。使用去除噪声的时间序列,构建训练样本集,将重构后的时间序列作为支持向量回归模型SVR的输入,进行进站客流预测。
2.3 模型评价准则
笔者采用以下预测评价指标:平均绝对值百分比误差(MAPE)、均方根误差(RMSE)、平均绝对误差(MAE)、决定系数(R2)和准确率(Accuracy)对模型进行评价。

式中,yi为i时刻的实际客流值;为i时刻对应的客流预测值;N为预测的样本数量;为i时刻客流真实值的平均值。
2.4 模型对比
为了验证SSA-SVR模型的高精度,笔者引入单一模型(ARIMA、SVR)以及组合模型(CNN-LSTM、T-GCN)作对比。ARIMA模型的使用前提是预测平稳时间序列,对于非平稳时间序列,需进行差分将其转化为平稳时间序列。SVR模型通过核函数将低维空间的数据映射到高维空间中,并对支持向量回归进行拟合。CNN-LSTM模型[16]中的CNN与LSTM分别作为两个通道输入,CNN通过卷积获取客流在空间上的特征和依赖,LSTM通过递归神经网络获取客流数据在时间上的特征和依赖,从而使模型能同时获得数据在空间维度和时间维度上的特征,并以时间序列预测的方式验证融合模型特征提取的有效性。T-GCN模型[17]由图卷积网络(GCN)和门控循环单元神经网络(GRU)组成,GCN用来学习复杂的拓扑结构以捕获客流的空间依赖关系,GRU学习客流数据的动态变化以捕获客流的时间依赖,将图卷积和门控循环单元融合起来以获取客流的时空依赖关系,并进行客流预测。为了增强说服性,对进站客流进行预测时,ARIMA、SVR模型应寻找最优参数,获得每个模型最优的预测效果,模型参数设置如表1所示。
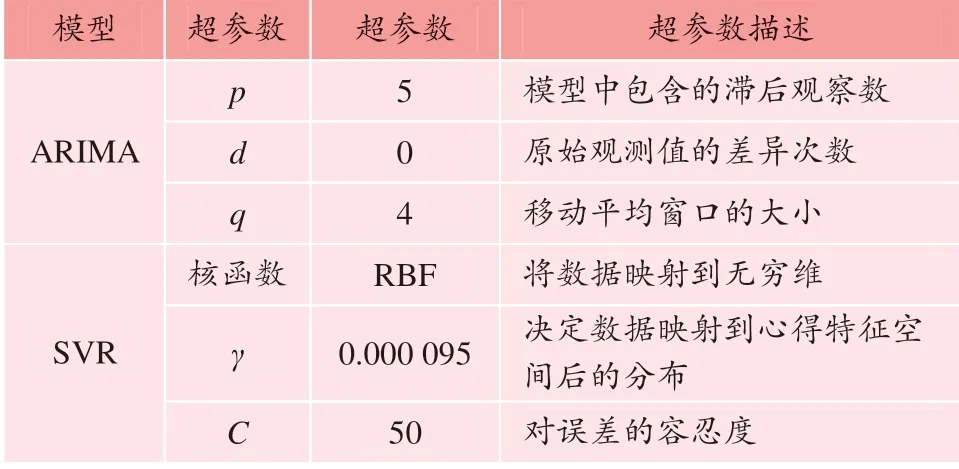
表1 对比模型参数设置Table 1 Comparison of the model parameter settings
分别从大、中、小三种量级站点中,选取6个典型站点作模型对比,大量级站点选取中关村、天通苑站点,中量级站点选取篱笆房、北新桥站点,小量级站点选取育知路、朝阳门站点,选取模型精度和均方根误差两个指标来评价模型,如图3所示。

图3 精度、均方根误差比较Figure 3 Accuracy and root-mean-square error comparison
以篱笆房站点为例,SSA-SVR模型的精度分别比ARIMA模型、SVR模型、CNN-LSTM模型以及T-GCN模型分别提高了16.0%、16.0%、12.0%和22.0%。由图3(b)可知,SSA-SVR模型的均方根误差分别比ARIMA模型、SVR模型、CNN-LSTM模型以及T-GCN模型降低了49.2%、46.7%、56.4%和40.8%。
由图4可知,中关村站和天通苑站两个站点的进站客流只有单峰趋势,且中关村站为晚高峰,天通苑站为早高峰,这与两个站点周围的用地性质相关。在大量级站点预测时,SSA-SVR模型的预测精度比ARIMA模型、SVR模型、CNN-LSTM模型以及T-GCN模型平均提高9.0%、10.5%、6.0%和17.0%。篱笆房站和北新桥站为中量级站点,在中量级站点预测时,SSA-SVR模型的预测精度比ARIMA模型、SVR模型、CNN-LSTM模型以及T-GCN模型平均提高12.5%、12.5%、10.5%和23.5%。育知路站和朝阳门站为小量级站点,在中量级站点预测时,SSA-SVR模型的预测精度比ARIMA模型、SVR模型、CNN-LSTM模型以及T-GCN模型平均提高9.5%、9.5%、6.0%和39.0%。
由以上指标可得,SSA-SVR模型对于短时客流预测精度的提高,在中量级站点明显优于其他模型。本文选取4种模型在不同量级典型站点的预测效果如图4所示。
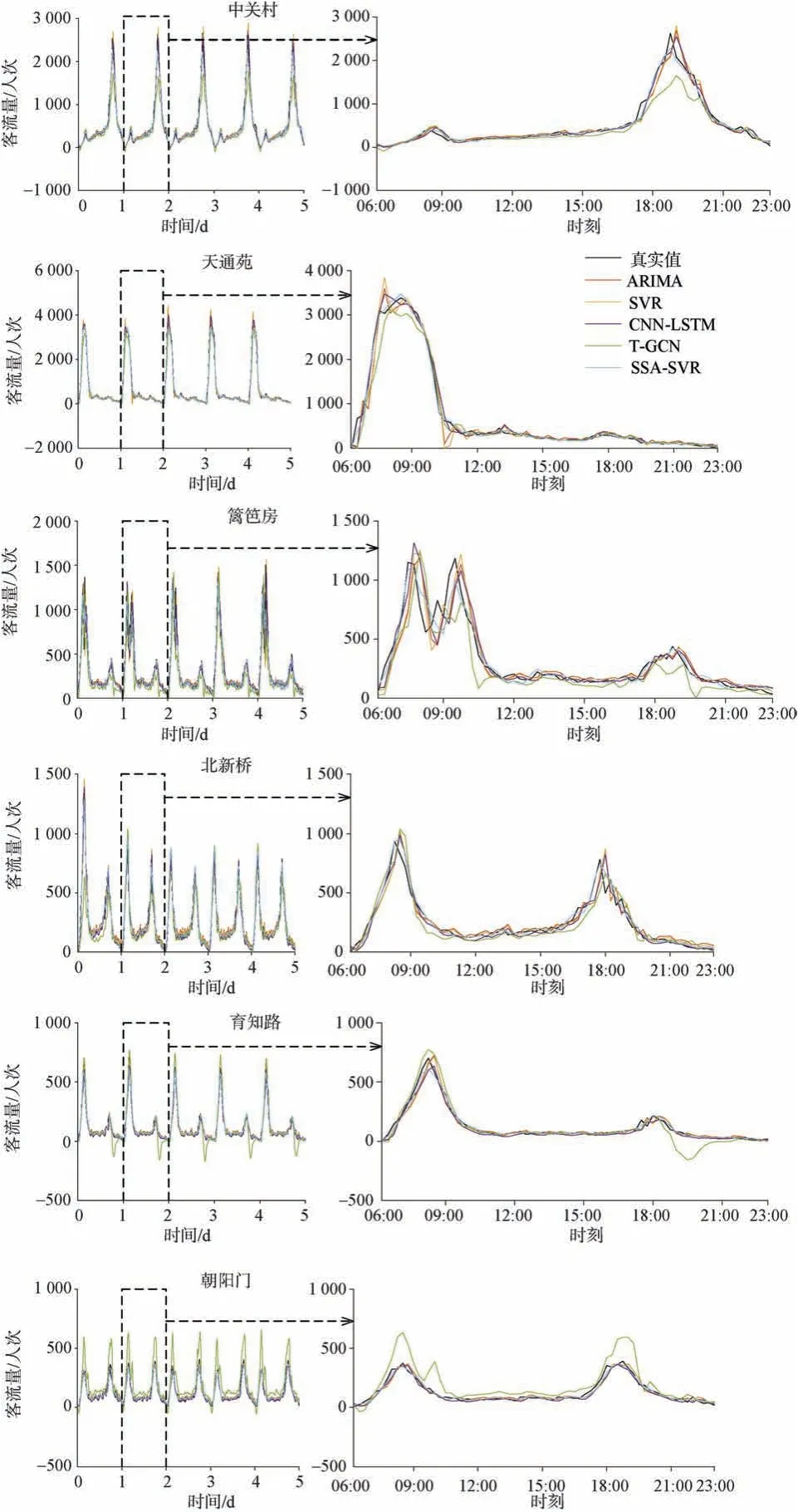
图4 典型站点进站客流预测模型对比Figure 4 Comparison of inbound passenger flow forecasting models for typical stations
实验模型的评价指标如表2所示,SSA-SVR模型的拟合度R2均在0.94以上,相同站点的拟合效果最佳。R2的值越接近1,说明真实值和预测值之间的拟合度越好,两者之间有更相似的变化趋势。
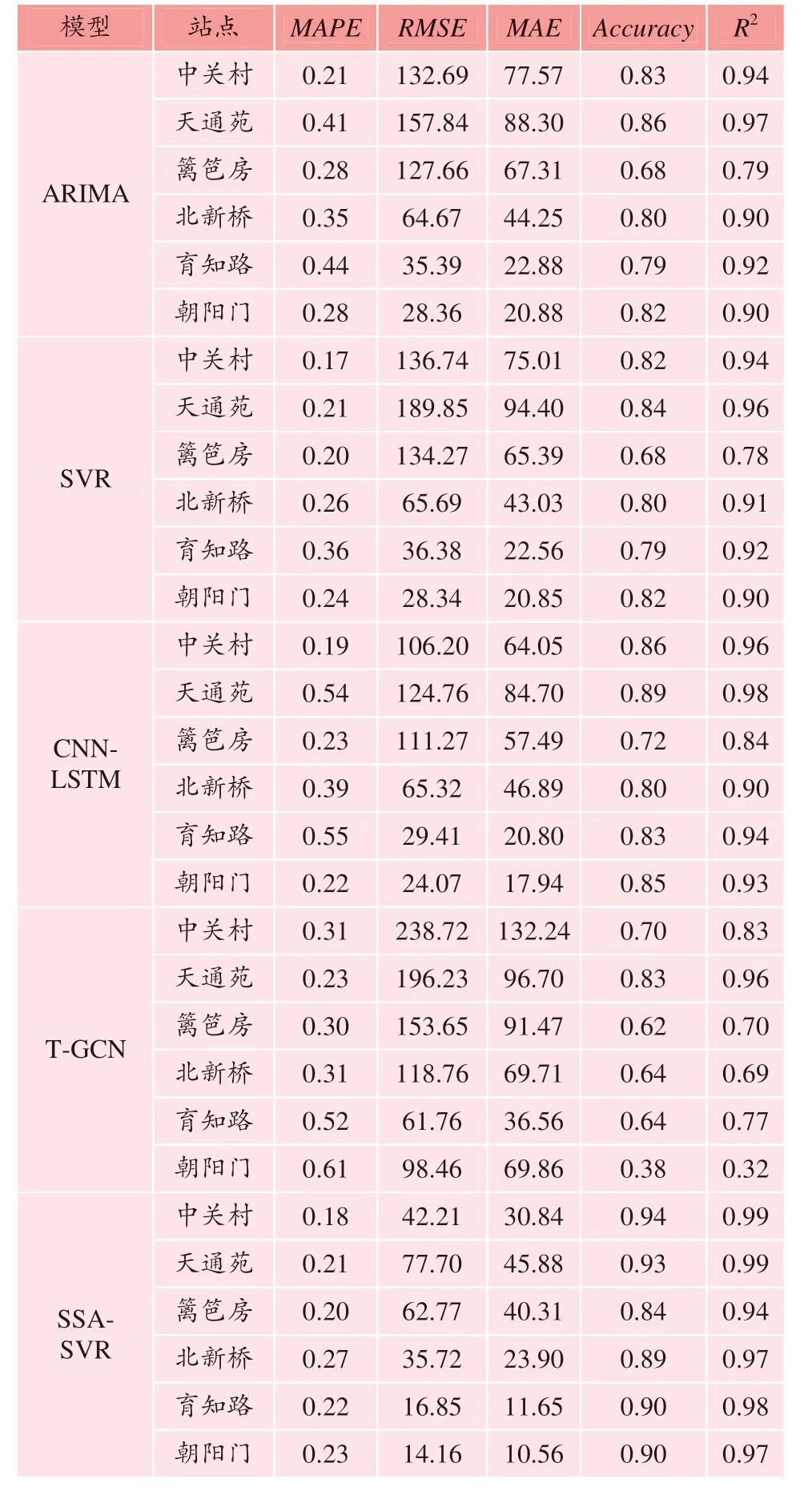
表2 模型指标实验结果Table 2 Experimental results of model index
综上所述,SSA-SVR模型在15 min轨道交通短时客流预测中表现出良好的预测性能和较好的稳定性,具有良好的泛化性。
3 结论
在对轨道交通短时客流预测时,SSA-SVR组合预测模型比单一模型和组合模型具有更高的精度和更稳定的预测表现。在数据具有较复杂非线性特征的轨道交通短时客流预测时,笔者所提出的模型具有可靠的依赖性。
轨道交通客流的特点是随机性和规律性,导致现有的大多数预测方法的精度不适用于预测地铁客流。SSA-SVR模型,结合了奇异谱分析和支持向量回归模型的优点,将原始客流进行SSA模型分解,提取出原始序列分解后的特征,重构交通流量序列,将重构的交通流序列作为SVR模型的输入条件,提高了模型的预测能力。
通过北京地铁进站客流数据进行验证,发现中量级站点预测精度没有大量级站点和小量级站点精度高,所以,后续的工作可以针对中量级站点的预测精度进行研究,笔者所提出的模型也可为其他领域时间序列预测提供参考。
