智能交通环境下多信息反馈效应的跟驰模型研究综述*
2023-01-04何金芳彭光含
邝 华,刘 晨,何金芳,彭光含
(广西师范大学物理科学与技术学院,广西 桂林 541004)
1 引言
车辆跟驰模型是交通仿真微观建模中一种重要的理论模型,也是目前交通流理论领域研究热点之一。车辆跟驰模型通常运用动力学方法,研究同一车道前后相邻车辆间的相互作用关系以及行驶状态变化趋势,从而达到描述交通流动态演化特性,揭示诱发交通阻塞、交通失稳、激波等非线性交通现象内在机理的作用。因此,车辆跟驰模型吸引了诸多学科领域(如交通工程学、力学、物理学、系统科学等)学者的广泛关注[1,2],并在交通仿真、交通安全评价和通行能力分析等方面得到广泛应用,具有重要的科学意义和工程应用价值。
20 世纪50年代初期,Reuschel[3]和Pipes[4]分别提出车辆跟驰的概念,并给出了车辆行驶动力学方程,标志着车辆跟驰理论的诞生。随后,学者们考虑各种因素(如心理因素、道路环境因素等)对交通流的影响,相继提出了各种不同微分方程形式的跟驰模型,研究了交通流中出现的各种非线性特性(如,时走时停、相变、密度波的形成和消散等),取得了丰硕的理论与实践成果。回顾跟驰模型近70年的发展历程,从建模方法的角度出发,可将跟驰模型分为两大类:理论驱动跟驰模型和数据驱动跟驰模型[5]。其中,理论驱动跟驰模型以车辆跟驰理论为基础,采用数理方法构建描述车辆动态特性的数学模型,通过对模型进行线性稳定性分析、非线性分析和数值模拟,探讨交通流演化机理。理论驱动跟驰模型的应用较为广泛,它主要包括刺激—反应模型(如GHR模型[6]、Newell模型[7]、IDM模型[8]、OV模型[9]、GF模型[10]和FVD模型[11]等)、安全距离模型(如Gipps模型[12]、CARSIM[13]和NETSIM模型[14]等)和生理心理模型(如Wiedemann模型[15]和Fritzsche 模型[16])。数据驱动模型不同于传统的微分方程模型,它不侧重数学推演,而关注交通数据样本的学习能力,通常采用非参数方法(如深度学习等)来挖掘交通流特性的内在规律。数据驱动模型主要包括模糊逻辑模型[17,18]和神经网络模型[19-21]等。
为了真实描述车辆的跟驰行为,学者们在跟驰模型中充分考虑驾驶员特性(如激进和谨慎驾驶[22]、记忆效应[23-30]等)、道路状况(如坡道[31-33]、弯道[34-36]等)、交通信息(如多速度差[37-41]、平均速度和间距效应[42-56]、鸣笛效应[57-60]等)和混合交通[61-66]等因素,提出了一系列车辆跟驰模型。近年来,随着智能交通系统(Intelligent Transportation System,ITS)的广泛应用及车联网、大数据等新技术的发展,大量学者开始在ITS环境下研究车辆的跟驰行为,跟驰模型在研究内容和研究方法上均呈现出新变化。本文聚焦理论驱动跟驰模型,深入梳理智能交通环境下多信息反馈效应(即,车辆可实时获取多前车行驶状态信息,并根据反馈信息合理调整自身车辆运行状态,以达到前后多车协同行驶的目的)跟驰模型的相关研究,明确多信息反馈效应的具体动力学特征,并对其发展趋势进行了展望。
2 经典跟驰模型简介
2.1 优化速度模型
1995 年,Bando 等[9]从动力学的角度出发,提出了应用广泛的优化速度(Optimal Velocity,OV)模型,该模型能够再现交通系统的失稳、交通阻塞、交通流的时走时停等复杂非线性现象。其动力学方程为:

式中,xn(t)和vn(t)分别是第n辆车在t时刻的位置和速度,是第n辆车在t时刻的加速度,a是敏感系数,∆xn(t)=xn+1(t)−xn(t)是第n辆车的车头间距。V(∆xn(t))是优化速度函数,且为车头间距∆xn(t)的函数,通常选取以下的双曲正切函数形式:

式中,vmαx是车辆行驶的最大速度,ℎc是车辆之间的安全距离。当∆xn(t)→0时,V(∆xn(t))→0;当∆xn(t)→ ∞时,V(∆xn(t))→vmαx,这表明优化速度函数具有单调递增且有上界的性质。
2.2 广义力模型
1998 年,Helbing 等[10]通过交通实测数据对OV 模型进行了参数辨识,发现OV 模型存在加速度过高和减速度不符合实际的问题,从而考虑近邻车辆负速度差的影响,提出了负速度差效应的广义力(Generalized Force,GF)模型,其动力学方程为:
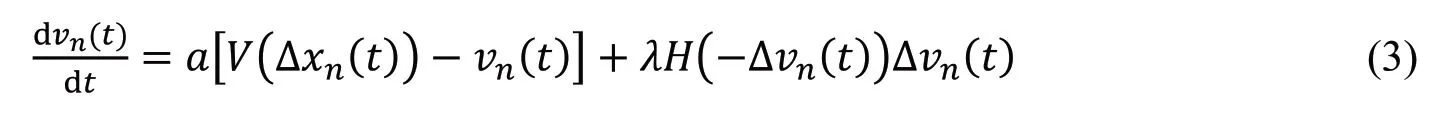
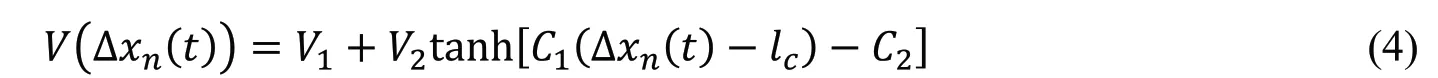
这里,V1=6.75m/s,V2=7.91m/s,C1=0.13m−1,C2=1.57m−1,lc为车身长度,通常取5m。
GF 模型解决了OV 模型中出现的与实际不符的加速度和减速度问题,更符合实际交通流运行状态,但由于仅考虑了负速度差效应对车辆跟驰行为的影响,故无法解释跟驰车的速度比前方最近邻车辆速度小很多时,尽管两车之间的距离小于安全间距,跟驰车也不减速这一真实存在的交通现象。
2.3 全速度差模型
2001 年,Jiang 等[11]通过同时考虑近邻车辆正速度差和负速度差的影响,提出了正、负速度差效应的全速度差(Full Velocity Difference,FVD)模型,其动力学方程为:
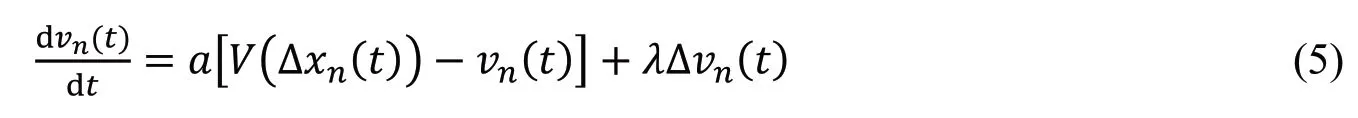
研究表明,FVD 模型在描述车辆跟驰行为等交通特性方面均优于OV 模型和GF 模型。
以上3 种经典跟驰模型,其动力学方程均可用以下一般形式描述:
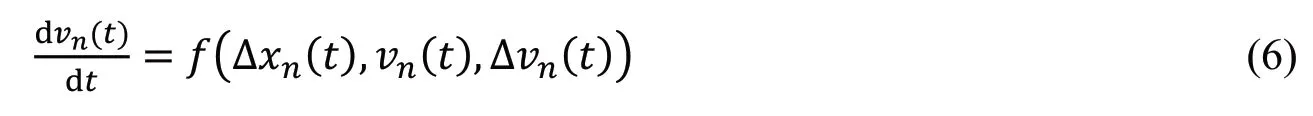
3 多信息反馈效应的跟驰模型
随着ITS的广泛应用和车联网技术的飞速发展,驾驶员能够通过车与车互联(Vehicle-to-Vehicle,V2V) 通讯设备实时接收道路前方多辆车的运行状态信息,而这些反馈信息必将对驾驶员的决策驾驶行为产生重要的影响,从而导致交通流呈现出复杂动态特性。因此,许多学者以OV 模型、GF模型和FVD 模型为基础,在智能交通环境下构建了多速度、多间距、多信息耦合的一系列多信息反馈效应的跟驰模型。
3.1 多速度信息反馈跟驰模型
(1) 多速度差效应
2006年,王涛等[37]考虑非邻近车辆的速度信息对交通流稳定性的影响,提出了多速度差跟驰模型,其动力学方程为:

式中,λl为速度差∆vn+l−1(t)的反应系数,且λl>λl+1。同年,Li等[38]在OV函数中引入多速度差变量,提出了考虑前方多速度差效应的跟驰模型,其动力学方程为:
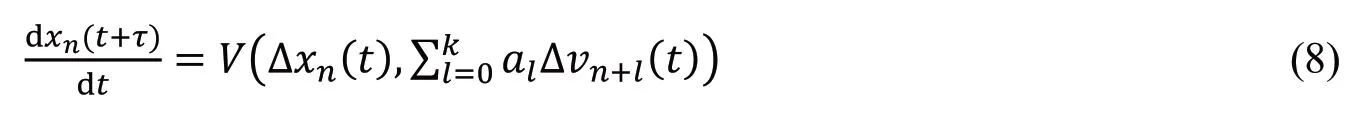
式中,al为加权系数。
2020 年,Zhang 等[39]借鉴Li 等[40]提出的自稳定控制思路(即,驾驶员具有记忆效应,驾驶员可通过调整车辆自身的历史速度vn(t)−vn(t −t0)来达到稳定交通流的目的),考虑前方多辆车连续自延迟历史速度信息对交通流的影响,提出了一个改进的跟驰模型,其动力学方程为:
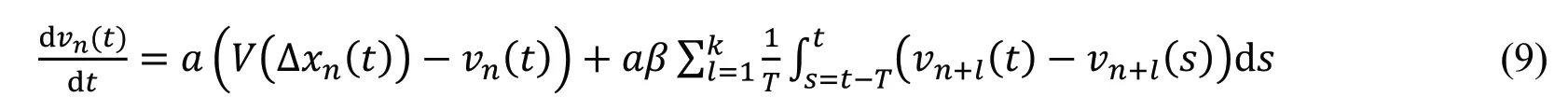
式中,T是延迟时间,β是反应系数。
2021年,Mei等[41]考虑前方多辆车自身不同时刻的速度信息,提出了多辆车历史速度效应的跟驰模型,其动力学方程为:
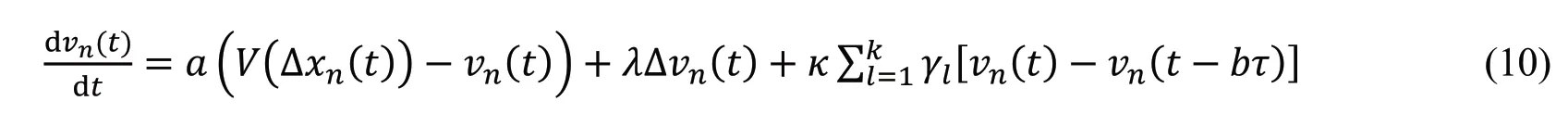
式中,γl是加权系数,κ是反应系数,τ是时间间隔。
(2) 多车平均速度效应
2015年,Sun等[42]考虑前方局域路段车辆的平均速度,提出了前方车辆群平均速度效应的跟驰模型,其动力学方程为:
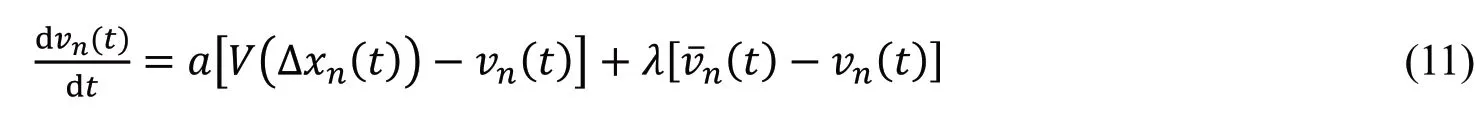
2018年,Zhu等[43]考虑前方局域路段车辆的优化速度,提出了平均期望速度场效应的跟驰模型,其动力学方程为:
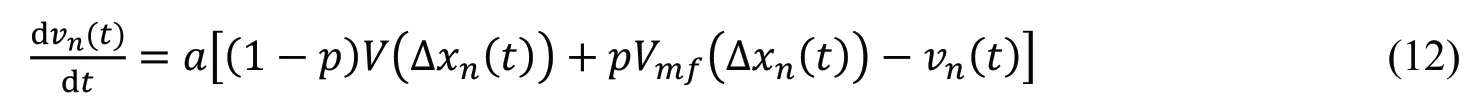
2019年,Kuang等[44]综合考虑前方局域路段车辆的平均速度效应和平均期望速度场效应,建立了多预期平均速度效应的跟驰模型,其动力学方程为:
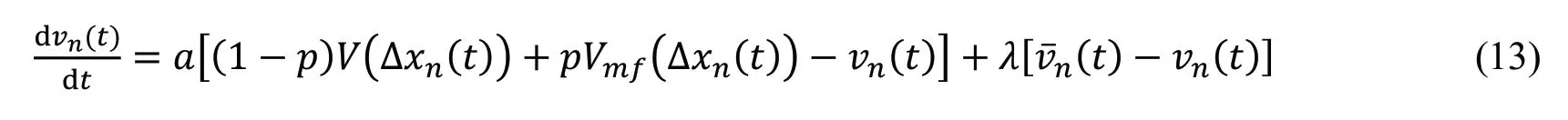
3.2 多间距信息反馈跟驰模型
鉴于车头间距对跟驰车的速度和行为会产生直接的影响,故大部分学者均在OV函数中考虑多间距效应。
2003年,Hasebe等[45]考虑前、后方多车辆相互作用,将OV函数推广到多个车间距变量,提出了一种多车协同驾驶的跟驰模型,其动力学方程为:

2004 年,Ge 等[46]考虑前方车辆间距信息的总体效应,提出了合作驾驶跟驰模型,其动力学方程为:
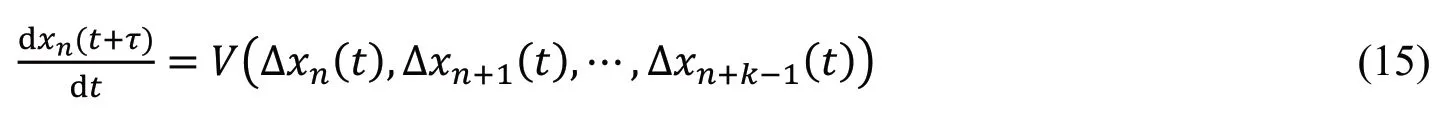
随后,Ge等[47]为区分前后车辆的运动状态,引入向后看的OV函数,提出了一个向后看效应的跟驰模型,其动力学方程为:
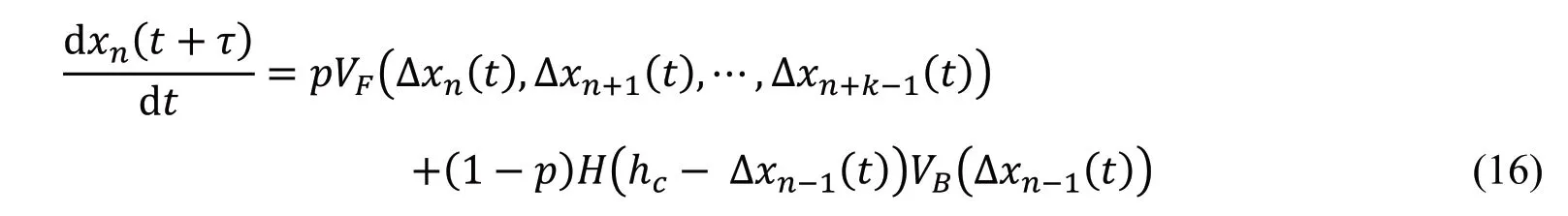
式中,VF为向前看效应的OV函数,VB为向后看效应的OV函数。
2017年,Kuang等[48]考虑前方车辆群的平均间距信息对交通流的影响,提出了平均间距效应的跟驰模型,其动力学方程为:
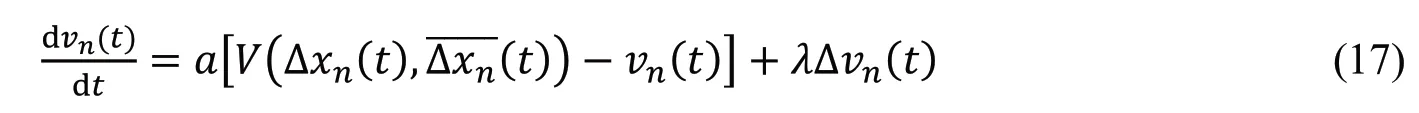
2021年,Zhang等[49]在车联网环境下,提出了前方多辆车空间预期效应的跟驰模型,其动力学方程为:
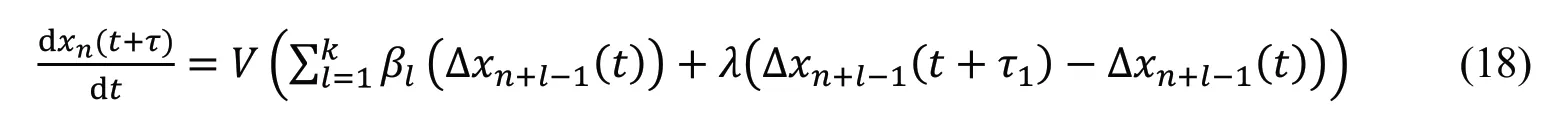
式中,βl是车间距的加权系数,τ1是预期时间。
3.3 多信息耦合跟驰模型
(1) 多间距和多速度差耦合
2008 年,Mo 等[50]提出了多间距和多速度差效应的跟驰模型,其动力学方程为:
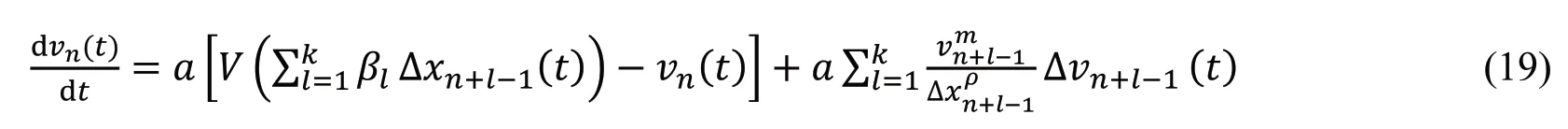
式中,βl是加权系数,m和p是待定参数,由实测数据确定其大小。
2010 年,Peng 等[51]综合考虑前方多辆车的间距信息和速度差信息,提出了一个扩展的跟驰模型,其动力学方程为:
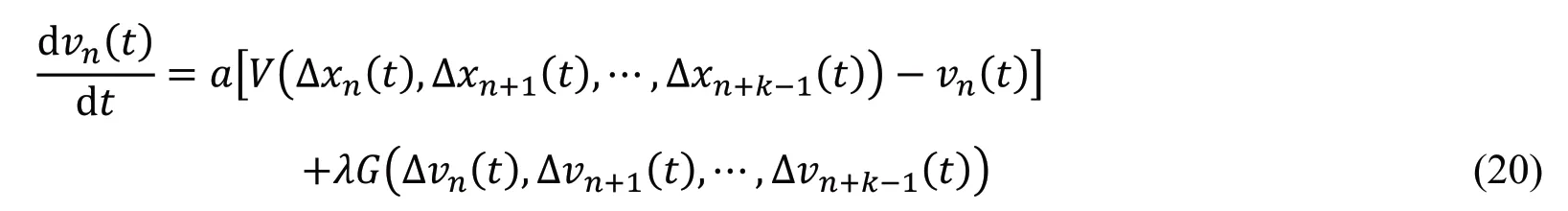
2014 年,Hu 等[52]综合考虑多速度差效应和驾驶员反应延迟效应,提出了多时延多车协同行驶的跟驰模型,其动力学方程为:

式中,τd为驾驶员的反应延迟时间,pl和ql是加权系数。
2016 年,Chen 等[53]基于Hu 模型[52],引入期望跟驰间距,提出了改进的多预期延迟效应跟驰模型,其动力学方程为:
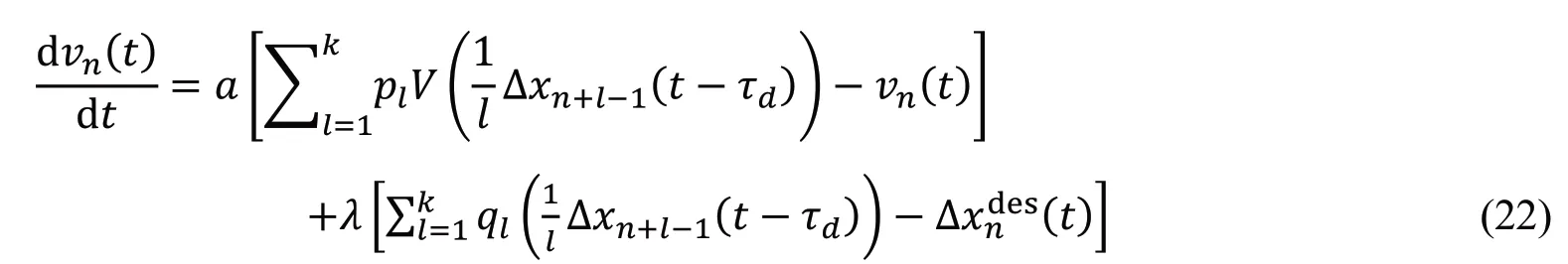
2018 年,Chen 等[54]从交通信息物理系统(Transportation cyber physical system,TCPS)的角度出发,考虑驾驶员的情境意识效应,提出了一个扩展的多预期多车协同驾驶的跟驰模型,其动力学方程为:
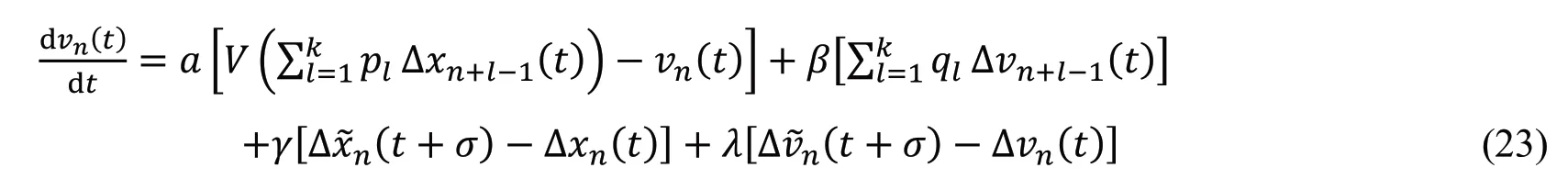
式中等式右边的第三和第四项反映了驾驶员对交通信息反馈后的决策驾驶行为,a,β,γ,λ是反应系数。
2022 年,Hossain 等[55]在Peng 模型[51]的基础上,考虑延迟效应,提出了一个改进的跟驰模型,其动力学方程为:

式中,w1和w2是加权系数,τ1和τ2是延迟时间。
(2) 记忆效应与多速度场耦合
2021 年,Kuang 等[56]综合考虑前方局域路段车辆的平均期望速度场效应和驾驶员的记忆效应对交通流的影响,提出了一个多信息耦合的跟驰模型,其动力学方程为:
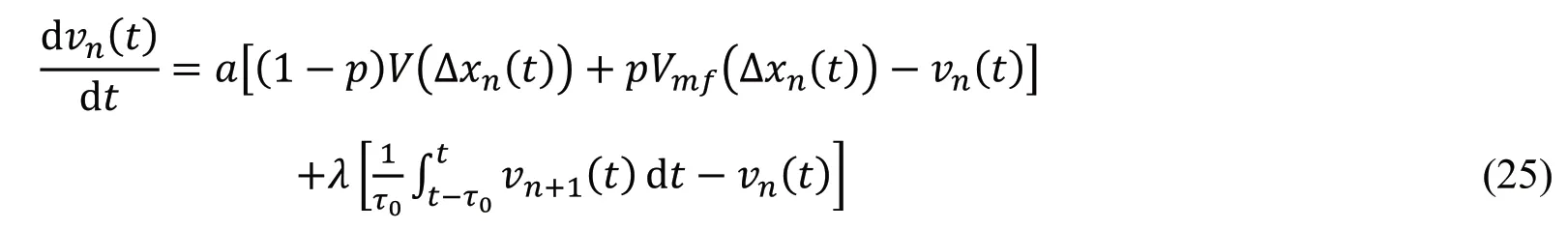
该模型可以描述驾驶员在[t −τ0,t]时刻内对车辆速度连续变化的记忆交通特性
以上各种多信息反馈效应的跟驰模型,其动力学方程均可用以下一般形式描述:
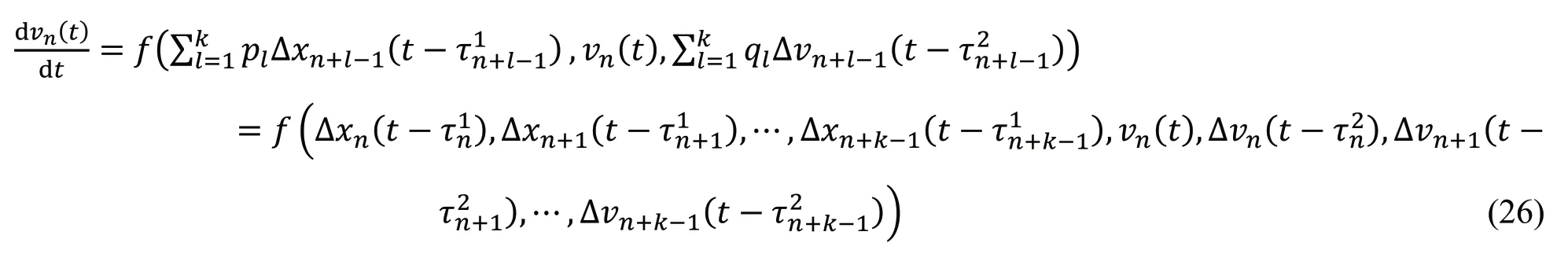
通过对多信息反馈效应跟驰模型的理论研究(如线性稳定性分析和非线性分析)和数值模拟表明,考虑多速度、多间距、多信息耦合的任意一种反馈效应均能够有效增强交通系统运行的稳定性,达到缓减交通堵塞的目的。
4 展望
多信息反馈效应跟驰模型在反映真实的交通系统方面具有非常大的潜力。随着车联网技术的大力发展,驾驶员对交通信息的感知能力将大幅提升,这必然会导致驾驶员展现出与以往不同的驾驶行为。此外,复杂的人为因素、道路条件(如限速、瓶颈等)和天气条件(如冰雪、大雾)等均会对驾驶员行为产生重要的影响。因此,现有的多信息反馈跟驰模型可以在以下几个方向进行改进,以提高ITS环境下交通仿真的真实性。
(1) 数据驱动跟驰模型研究
随着大数据时代的到来,数据驱动跟驰模型(如基于深度学习的跟驰模型、模型与数据混合驱动的跟驰模型)得到快速发展,如何将多信息反馈机理扩展应用到数据驱动跟驰模型中具有重要意义,其研究可为无人驾驶技术发展提供重要理论依据。
(2) 智能网联环境下混合交通流跟驰模型研究
随着车联网技术的发展,未来很长一段时间内将出现网联自动驾驶车辆、自动驾驶车辆和人工驾驶车辆混合行驶的情况,因此智能网联环境下混合交通流跟驰模型的研究必将成为智能交通研究的热点,而如何将多间距、多速度差、多前车行车状态数据传递失效和网络时延等因素融入到混合交通流的动力学建模中至关重要,其混合交通流的动态特性分析对于混合交通系统的稳定控制和交通拥堵的缓解具有重要作用。
(3) 基于人为因素的跟驰模型研究
在多信息反馈效应建模方面,充分考虑驾驶员的心理和生理特性(如驾驶习惯等)来描述与人类驾驶行为相关的交通现象仍是今后研究的方向和重点。
(4) 基于交通环境的跟驰模型研究
跟驰车辆的驾驶行为不仅取决于同一车道前车的驾驶行为,还与交通运行环境(如道路条件和天气条件等)有关,例如,大雾天气能见度低、冰雪天气易诱发车辆侧移等,这些因素将会直接影响驾驶员的跟驰距离和速度,进而导致驾驶行为和交通运行状况的巨大差异。此外,在多信息反馈作用下,建立多车道车辆跟驰模型,探讨车辆的纵向跟驰行为和横向换道行为还有待深入研究。
5 结论
车辆跟驰模型一直是交通流理论的研究热点,通过对车辆跟驰行为微观建模与仿真研究,有利于深入揭示交通流的运行机理,从而为交通规划与管理、道路通行能力、无人驾驶技术发展等提供理论支撑。本文阐述了跟驰模型的产生与发展,重点介绍了智能交通环境下多信息反馈效应跟驰模型的相关研究,并指出了今后在数据驱动、混合驾驶、人为因素和交通环境四个方面需要进一步研究的内容和问题,可为大数据人工智能时代的智慧交通研究提供有益的参考。
