GEO卫星在轨服务路径规划方法
2023-01-04王新波赵险峰
王 涛 张 锴 王新波 赵险峰
中国人民解放军32032部队,北京 100094
0 引言
卫星在轨服务内容涵盖在轨维修、在轨组装、在轨救援、空间碎片清理等领域,是航天领域发展的重要方向之一。
在轨服务可看作轨道交会问题。霍曼转移及其衍生变轨方法计算便捷,但适用范围有限。对于一般的二体交会,兰伯特变轨应用更加具有普适性[1]。蔡远文等[2]给出了漂移式、组合式和直接弹道式三种共面轨道机动方法,可为多目标交会任务提供支撑。多目标交会任务超出了轨道机动的范畴,涵盖了目标选择与路径优化, Shen等[3]针对圆轨道“一对多”服务场景,指出最优服务方式是顺时针或者逆时针依次交会。罗亚中等[4]、Alfriend等[5]、欧阳琦等[6]、余婧等[7]、韩鹏等[8]、解树聪等[9]等以在轨加注、空间碎片清理等为背景,将该问题描述为一个优化问题,分别采用序列二次规划、遗传算法、混合优化算法、最优控制理论、机器学习等方法进行求解。Zhao等[10]进一步研究了考虑地球非球形摄动与月球引力的GEO卫星在轨服务问题。以上学者直接采用优化方法对多目标交会问题进行求解,没有与工程轨道机动算法充分结合,导致计算量较大。
本文基于工程轨道机动策略研究GEO卫星在轨服务路径规划问题,针对目标星序列(文献[3]给出最优序列为顺时针或逆时针),采用合适的轨道机动策略,在给定的时间内使卫星沿着设计路径与目标交会。
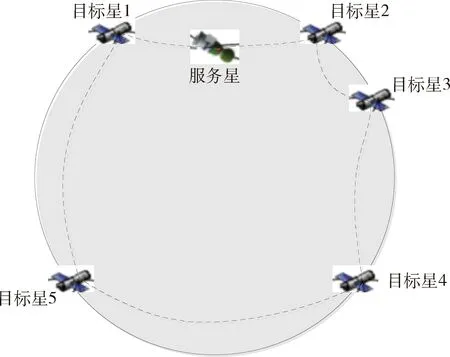
图1 卫星“一对多”在轨服务
1 目标交会策略
1.1 霍曼变轨式调相
利用霍曼变轨原理设计轨道调相方法,通过两次切向推力冲量调整服务星的轨道半长轴,利用服务星与目标星的轨道周期差实现相位调整,从而抵近目标星,如图2所示。
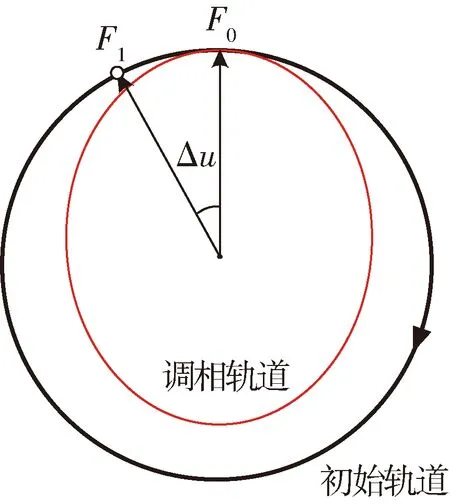
图2 霍曼变轨式调相
服务星在初始圆轨道F0点施加Δv1,进入调相轨道,在调相轨道上运行一圈后,在F0施加第二次机动冲量Δv2,卫星回到初始轨道,调相时间为一个调相轨道周期,即
tm=Tm
(1)
如果不进行调相,服务星在tm时间运行至F1,因此卫星在调相轨道运行一圈的相位调整量
(2)
式中,a0为初始轨道的半长轴;n0为角速度。
根据Δu可计算调相轨道的半长轴am
(3)
通过对比初始轨道与调相轨道在F0的速度,可得到速度增量
(4)
1.2 漂移式调相
服务星首先通过霍曼转移进入调相轨道,在调相轨道运行多圈后,再次通过霍曼转移返回到初始轨道,共需2次霍曼转移4次轨道机动,如图3所示。
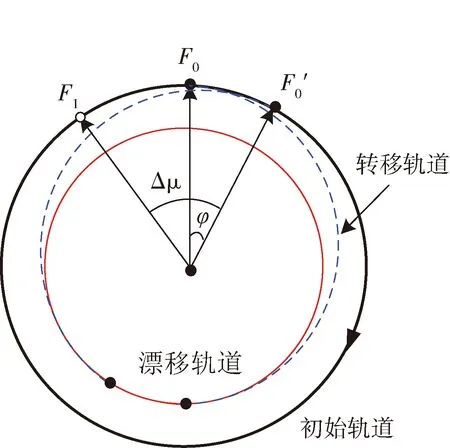
图3 机动漂移式调相
调相轨道包含两段霍曼转移轨道和漂移轨道。假设服务星轨道半长轴为a0,漂移轨道半长轴为am,则转移轨道半长轴at=(a0+am)/2。调相时间包含在转移时间和漂移时间,转移时间为一个转移轨道周期,漂移时间取决于服务星在漂移轨道上的飞行弧长,假设任意弧长可表示为2Nπ+φ,则调相时间为
(5)
式中,Tt为转移轨道周期;Tm为漂移轨道周期;N为在调相轨道上的飞行圈数。则相位调整量为
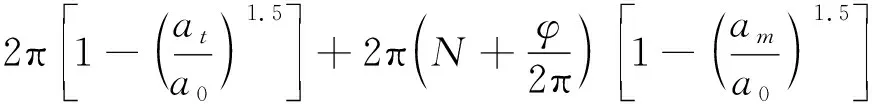
(6)
已知Δu,通过方程(6)可求解角度φ。
(7)
式中,通过调整N,使φ小于2π。
速度增量可由霍曼转移公式计算
(8)
式中,nt为转移轨道角速度。
服务星的机动燃耗、漂移时间与半长轴调整量紧密相关,如图4,调相所需的速度增量与a0-am成正比,调相时间随a0-am单调下降,曲线斜率逐渐减小。因此调相时间和速度增量是一对矛盾,在实际应用中需根据具体任务进行权衡。
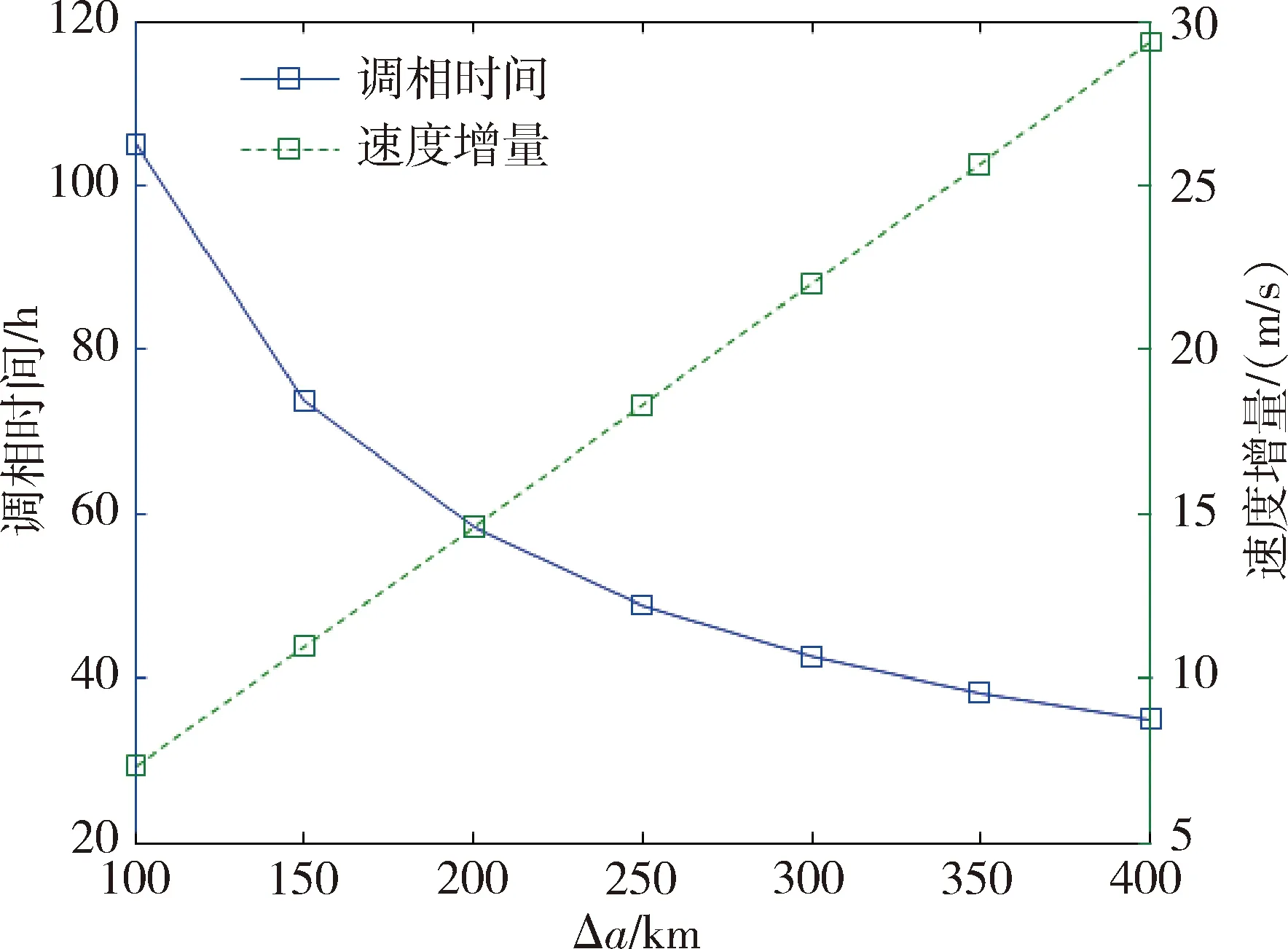
图4 调相时间/燃耗随轨道高度差的变化
1.3 径向机动式调相
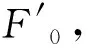
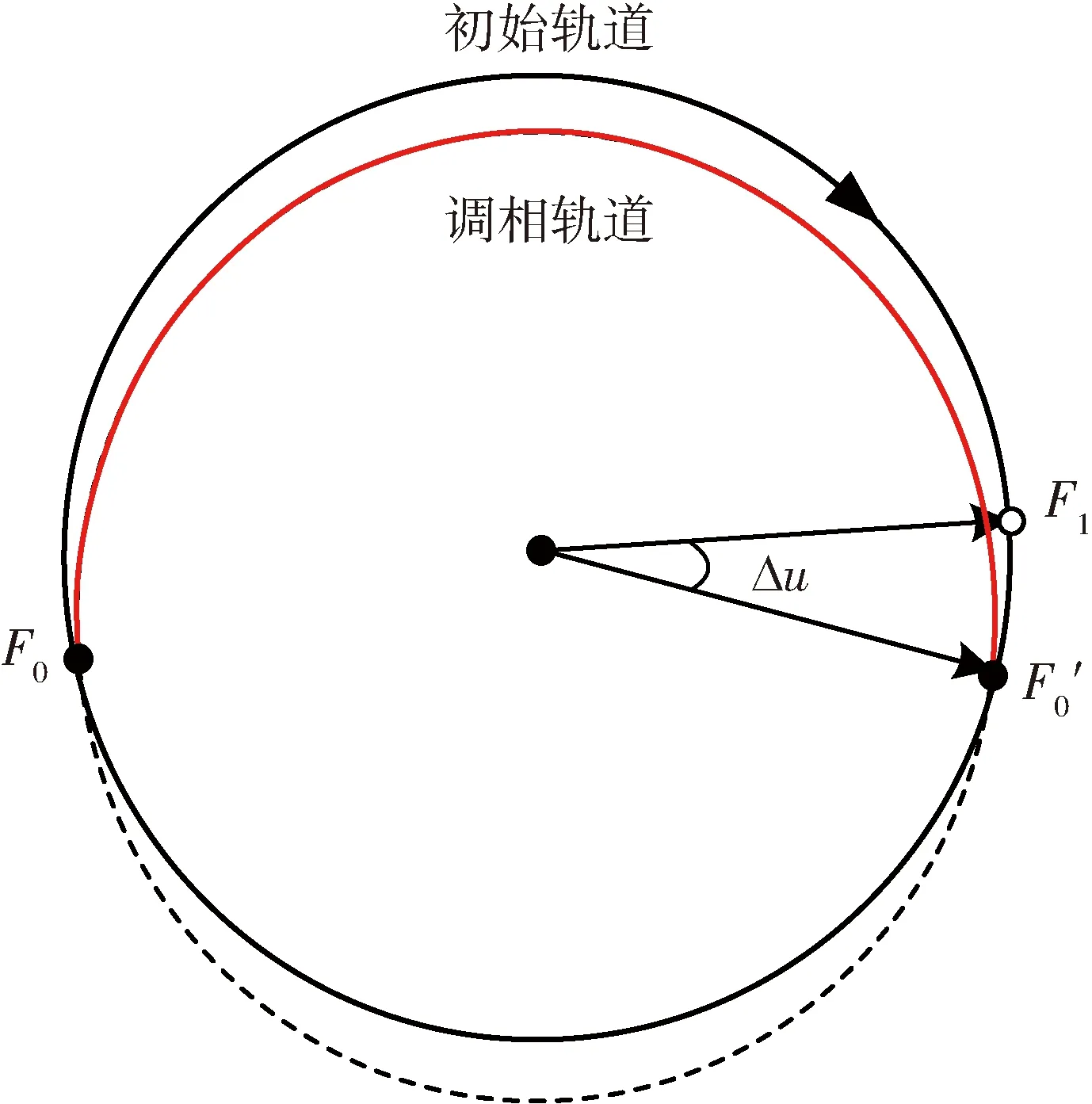
图5 径向推力机动调相
当采用径向冲量变轨时,根据高斯摄动方程可得

(9)
对于GEO,由于e≈0,所以径向冲量对Δa影响很小,主要改变偏心率。
已知F0的地心矢径等于初始轨道半径
(10)
由于半长轴基本不变,所以at≈a0,代入式(10)得
cosf≈-Δe
(11)
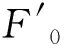
(12)
由偏近点角可进一步求平近点角,因此tm的表达式如下
(13)
相位调整量可表示为
Δu=2f-tmn0=
π-2arccosΔe+2Δe
(14)
已知Δu,可求出Δe,然后由方程(9)求出Δvx。
1.4 兰伯特变轨调相
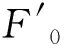
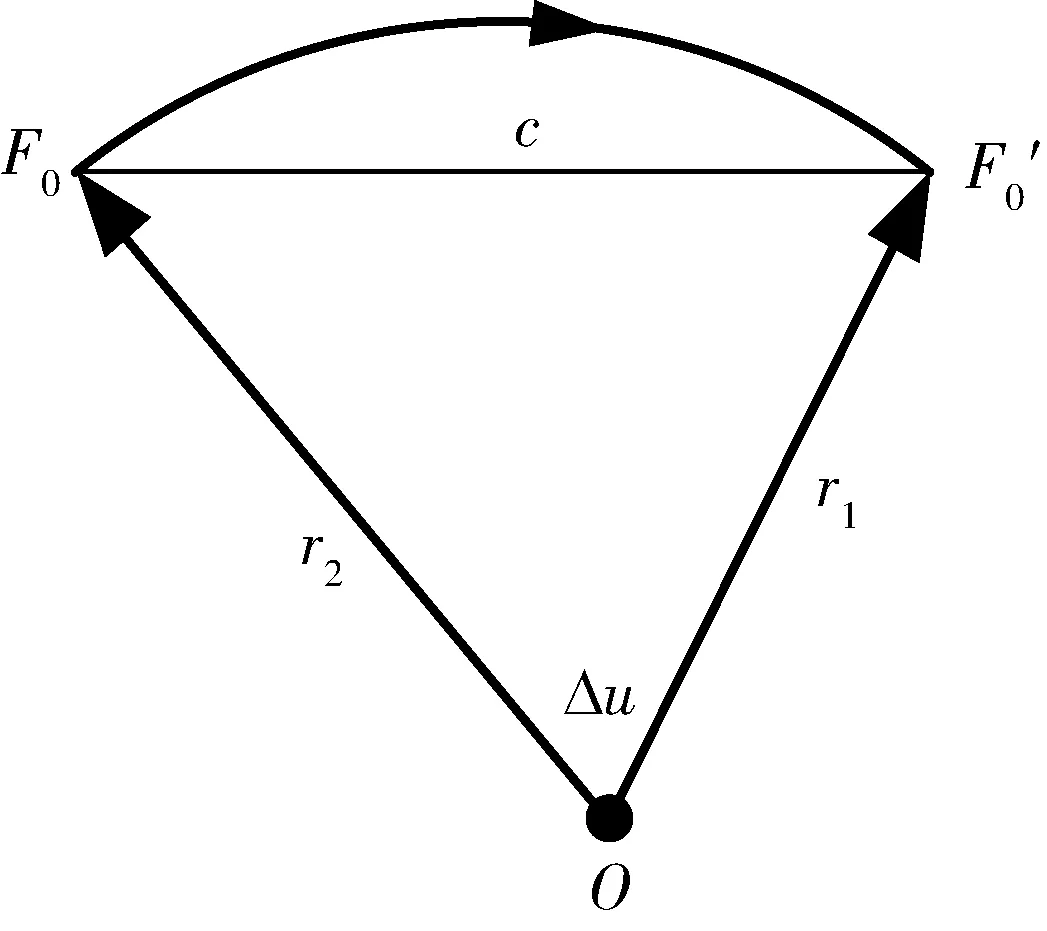
图6 兰伯特问题描述
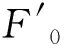
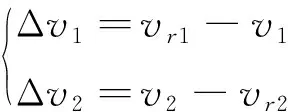
(15)
2 飞行路径规划
已知目标星数量为M,采用一个服务星对所有目标卫星进行服务,服务星燃料总量为ΔV,服务时限为tmax。通过优化设计使燃料消耗最小。
2.1 交会策略选取方法
兰伯特式调相方法包含一个时间自由量,如图7,机动冲量随调相时间而减小。经过对调相时间和机动冲量的权衡,当调相时间tm=9h,效费比较高。
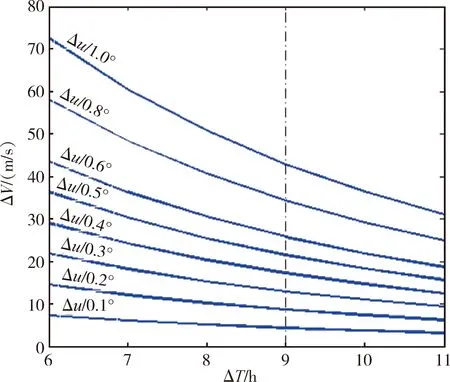
图7 兰伯特式调相速度增量与时间的关系
图8中,随着Δu增大,漂移式调相方法的速度增量保持不变,其它三种方法的速度增量线性增加,其中兰伯特调相方法增加最快。
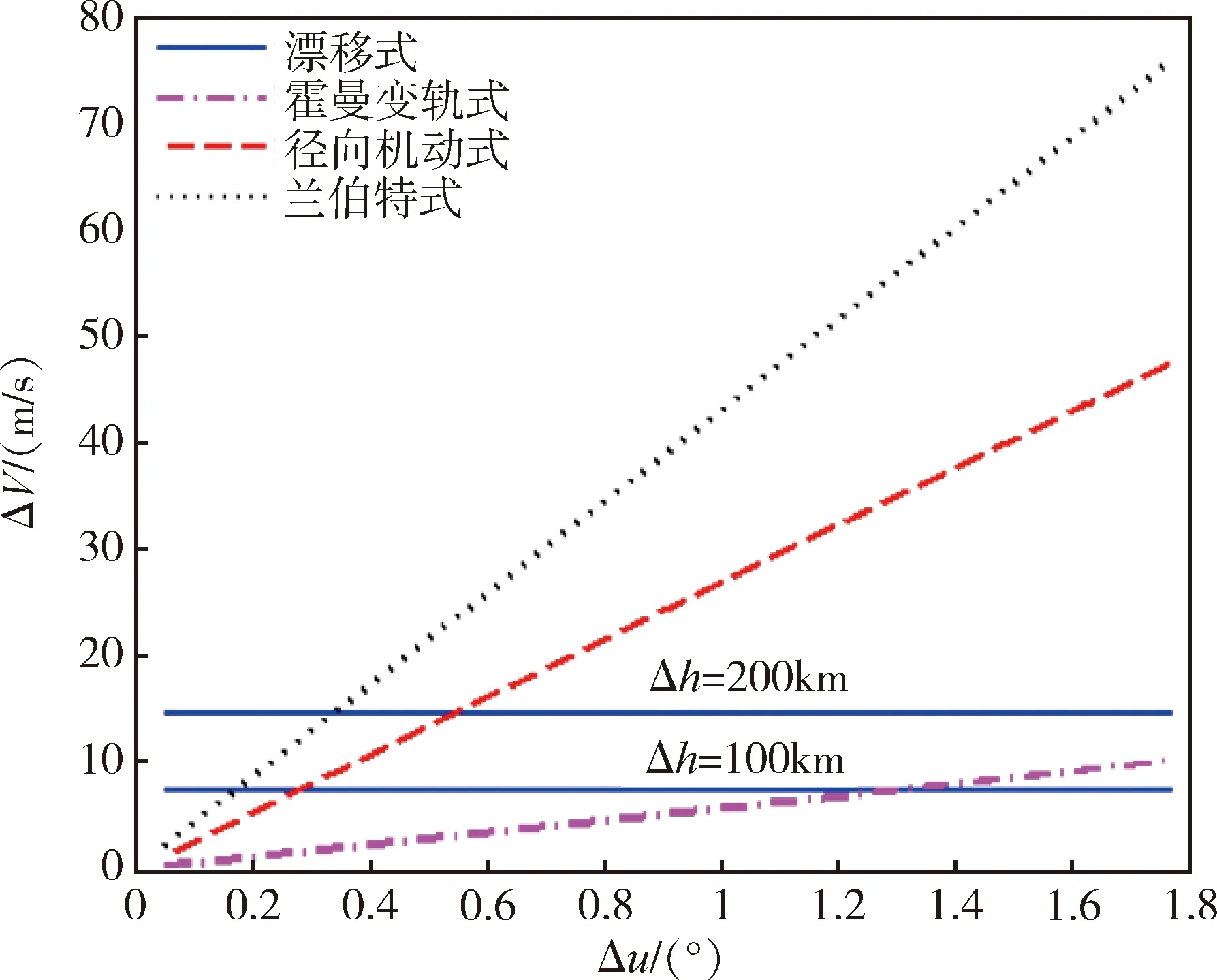
图8 四种调相方式速度增量对比
结合图8,考虑4种方法的机动冲量和调相时间,设计如下策略:
当Δu0>1.2°(大于840km),采用机动漂移调相方法;
当0.25°<Δu0≤1.2°(175km~840km),采用霍曼变轨调相方法;
当0.15°<Δu0≤0.25°(105km~175km),采用径向调相方法;
当Δu0≤0.15°(小于105km),采用兰伯特调相方法。
2.2 机动冲量计算
1)首先确定目标星序列,根据目标星在GEO的经度进行顺时针或逆时针排序;
2)假设服务星与M个目标星交会时间依次为{t1,t2,…,tj,…,tM};
3)服务星从当前位置,抵近下一个目标星j,根据Δuj的大小选择需要采用调相方法;
4)基于选定的调相方法,由tj和Δuj求解Δvj;
5)判断是否为最后一个目标,如果不是,转到3),如果是,转入6);
6)计算整个任务的轨道机动速度增量∑Δvj。
2.3 遗传算法优化
采用MATLAB遗传算法工具箱求解最省燃料飞行路径。
适应度函数:J=∑Δvi
优化变量M个:{t1,t2,…,tj,…,tM}
等式约束:∑tj=tmax,tmax为服务完成时限
非线性约束:单次机动冲量Δvi≤ΔVlim,ΔVlim为单次机动最大冲量。
遗传算法中,种群规模设置为50,其它参数设置为默认值。
3 仿真案例
服务星初始轨位为48°,目标星轨位分别为[50;59;60;60.12;60.5;125;128;129.93;130;160; 160.2]°,要求在60天内,实现对所有目标星的抵近交会,且燃料消耗最小,单次轨道机动冲量小于5m/s。
采用文中的方法进行优化求解,得到服务星对每个目标星的交会用时,t=[4.065,8.062,1.000,0.500,1.000,20.708,4.867,4.002,0.375,14.294,0.5]d,完成任务的总速度增量为48.476m/s。服务星每次调相的速度冲量如表1所示,采用该机动冲量序列计算服务星飞行曲线,如图9所示,红色方框为目标星位置,服务星能够与11个目标星成功交会。
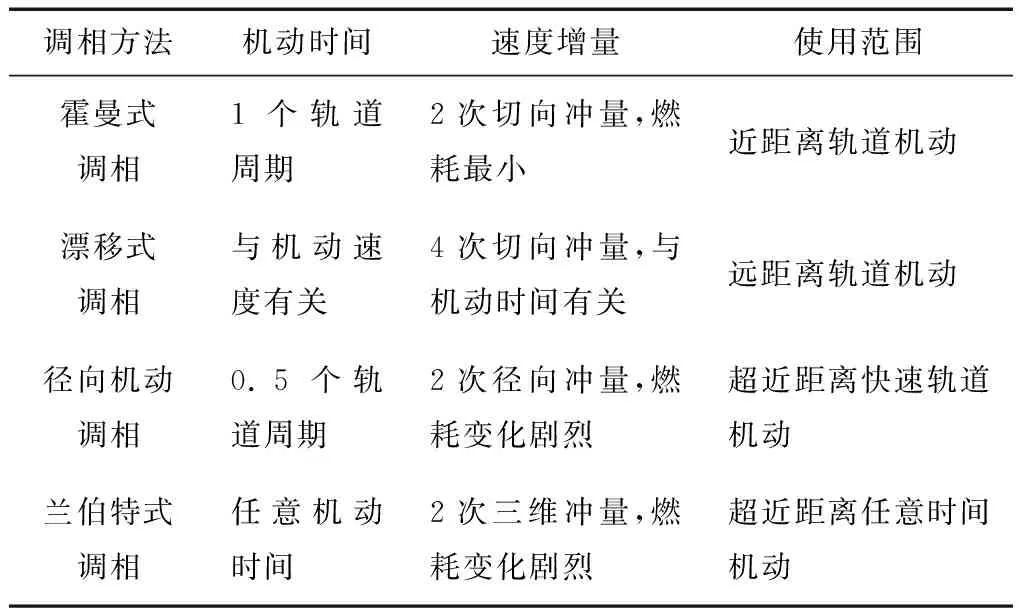
表1 四种调相方法对比
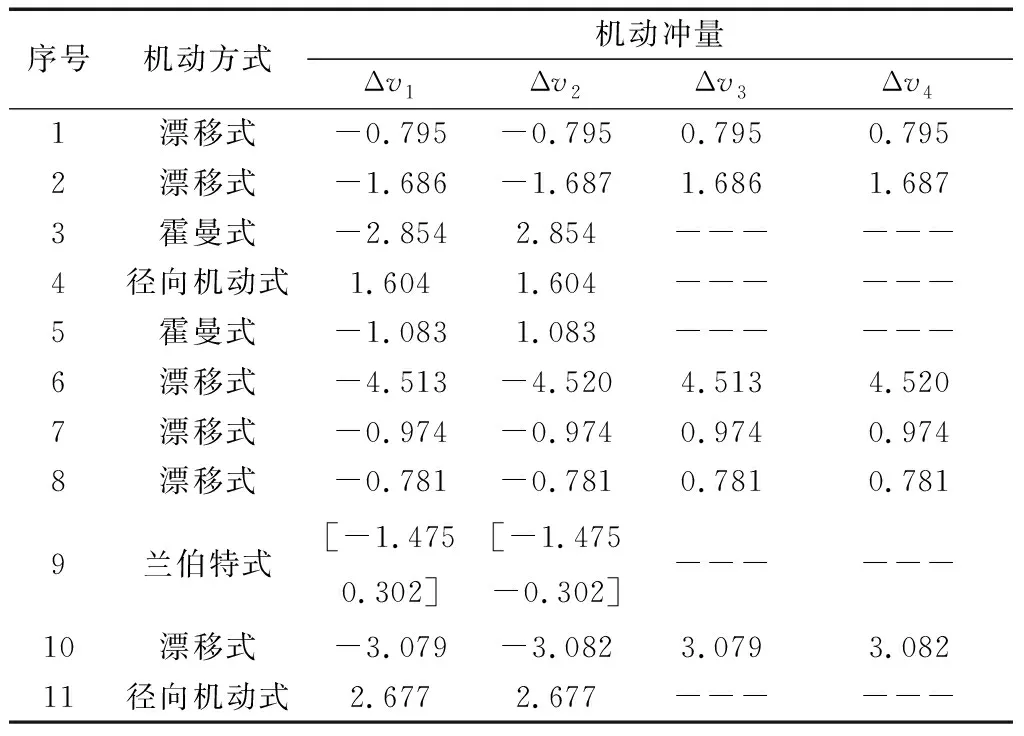
表2 在轨服务任务的机动冲量
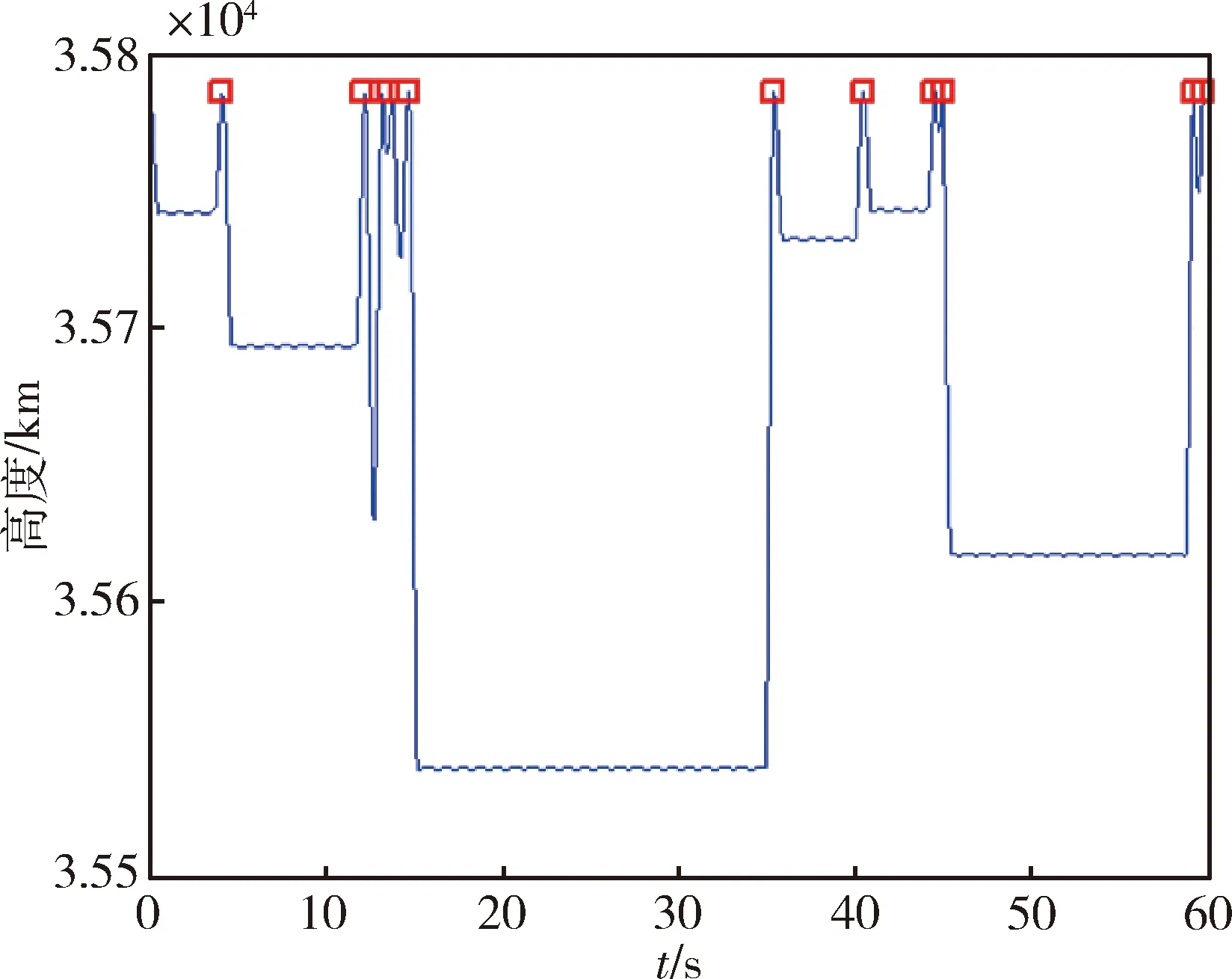
图9 服务星飞行高度曲线
将任务要求时间分别调整为50d、70d、80d,基于遗传算法进行优化计算,求出速度增量分别为59.412m/s、40.998m/s、35.563m/s,开展数据拟合,得出如下曲线。在65d时,效费比最高。
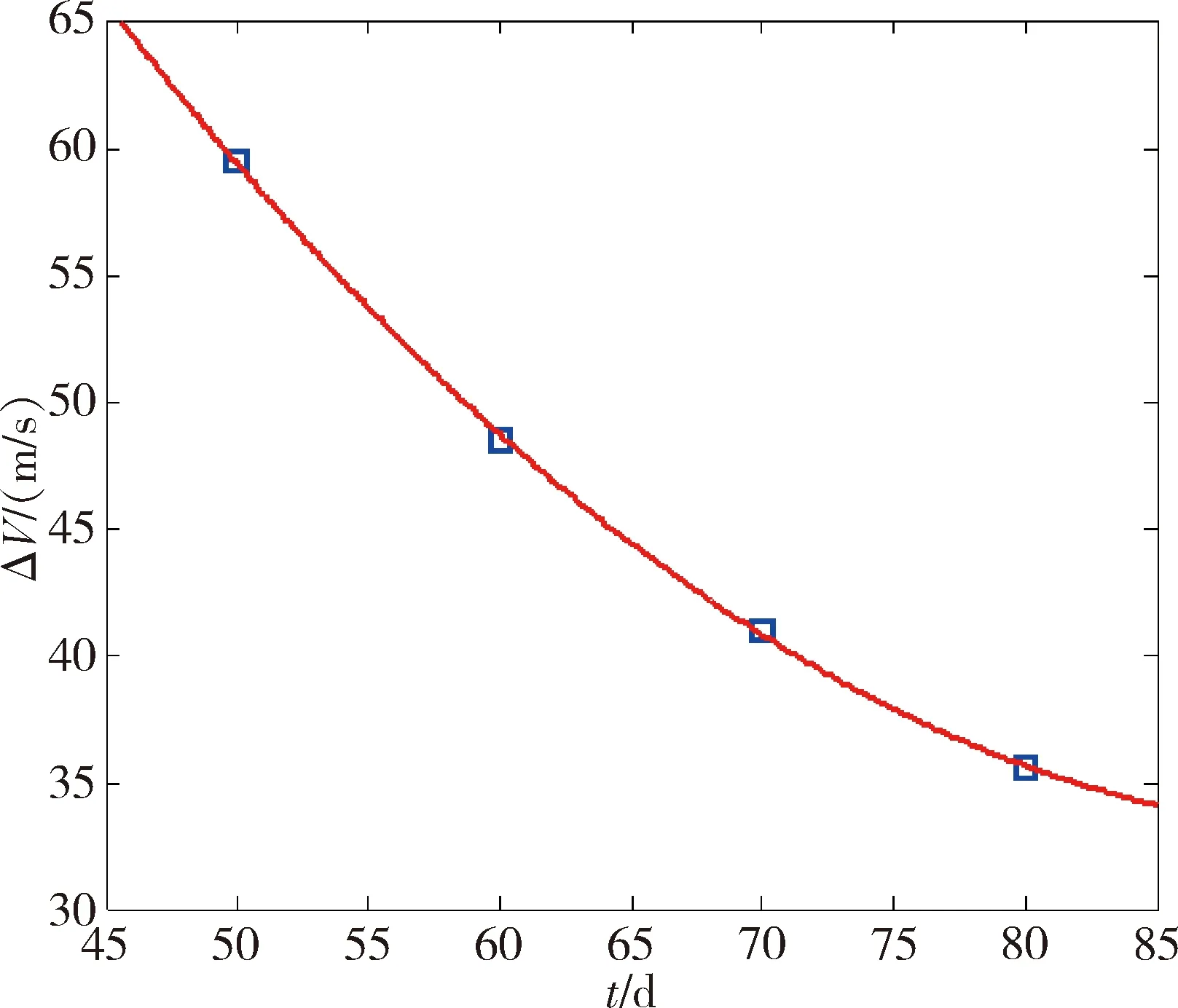
图10 总速度增量与任务完成时间的关系
4 小结
本文提出了一种GEO卫星在轨服务路径规划方法,具有较高的工程应用价值。
1)基于实际工程中卫星轨道机动方法开展研究,能够将卫星任务规划系统与其轨道机动能力紧密结合。
2)对比分析了4种轨道调相方法,提出了不同交会距离下选取轨道调相方法的规则。
3)避免了对每次轨道机动的机动冲量大小、方向的优化,优化变量大幅度减少,计算速度加快。
