变形飞行器深度强化学习姿态控制方法研究

马少捷 惠俊鹏 王宇航 张 旋

1. 中国运载火箭技术研究院研究发展部，北京 100076 2. 北京航天长征飞行器研究所，北京 100076

0 引言

变形飞行器可以根据飞行任务、飞行环境不同适时自主改变气动外形，实现全剖面飞行性能优化，同时以不同气动布局满足不同飞行任务需求，对飞行器跨域飞行、多任务适应具有重要意义[1-2]。但由于其变形过程中气动参数、结构参数呈现非线性变化的特点，变形引起的惯性附加力、附加力矩难以忽略，同时变形结构刚度差导致气动、结构耦合现象严重，使得变形飞行器模型具有较大的不确定性，并且变形过程中飞行器受外界干扰因素影响较为复杂，对控制系统设计提出了挑战。另一方面变形飞行器为了达到飞行剖面的性能最优，需要在执行任务中实时决策变形指令，而传统算法控制器参数离线设计、在线插值的方式难以达到理想控制效果。

针对该问题，有学者基于线性模型提出了反馈控制[3]、切换线性变参数(Linear Parameter Varying, LPV)鲁棒控制[4]等方法，却在一定程度上损失了变形飞行器模型的非线性特征。因此滑模控制[5]、动态逆控制[6]等非线性控制方法成为主流研究方向，这类方法更大程度地保留了控制系统模型的非线性特征，但同时也存在对模型准确度依赖较高的问题。此外，宋慧心等[7]基于自抗扰控制理论开展控制器设计，取得了较好的控制效果，但自抗扰控制参数整定问题增加了控制器设计的复杂度。因此迫切需要适应性、鲁棒性更强的控制算法来提升控制系统品质。

随着人工智能技术发展，强化学习作为一类数据驱动的智能算法，通过智能体与环境的交互，从数据中训练得到控制策略，不依赖于精确的控制模型，突破了复杂系统精确建模困难的局限，为复杂控制系统设计提供了新的解决途径，逐渐应用于复杂条件下飞行器制导控制系统设计[8-11]中，其中代表性的算法是深度确定性策略梯度(Deep Deterministic Policy Gradient, DDPG)算法。Wang等[12]针对吸气式飞行器姿态控制问题，基于DDPG算法在线优化反步法控制参数。Wang等[13]针对四旋翼无人机的高度控制问题，基于DDPG算法直接进行策略训练，最终实现状态量到执行动作的端到端控制。DDPG算法在无人机姿态控制中具有良好的鲁棒性与强泛化能力，然而算法本身存在值函数过估计、算法稳定性差等问题，Fujimoto等[14]提出的双延迟深度确定性策略梯度(Twin Delayed Deep Deterministic Policy Gradient, TD3)算法，在算法稳定性与收敛性方面有更好的效果。

本文在上述研究的基础上，基于TD3算法提出了一种变形飞行器姿态控制方法。以一类机翼可伸缩的变形飞行器为对象，考虑其多刚体结构，建立了纵向平面数学模型，然后在马尔可夫决策过程(Markov Decision Process, MDP)的框架下设计了算法训练所需的状态空间、动作空间以及网络结构，还设计了一种兼顾控制精度与能量需求的奖励函数，并在状态空间中引入姿态跟踪误差的历史信息，减小了值函数估计误差引起的稳态误差，将策略网络与PD控制器结合形成复合控制器，提高了算法的训练效率，最后通过数学仿真验证了所得控制策略的适应性与强鲁棒性。

1 变形飞行器数学模型

考虑一类伸缩变形飞行器，其局部外形如图1所示，其左右机翼可以沿翼展方向水平伸缩，最大翼展可达到本体的2倍，变形量通过翼展变形率ξ=Δl/l表示，其中Δl为伸缩机翼伸出长度，l为本体翼展，ξ∈[0,1]。

假设伸缩机翼对称匀速变形，且变形翼只在水平面内伸缩，将飞行器分为机体、左右伸缩机翼3个结构，以飞行器机体质心为参考点，基于Kane多体动力学建模方法建立变形飞行器动力学模型，如式(1)。

(1)

式中，m为飞行器总质量，I为飞行器总转动惯量，Vb为质心坐标系下的运动速度，ω为飞行器旋转角速度，F和M分别为飞行器所受合外力、合外力矩，Fs和Ms分别为飞行器变形附加力和附加力矩。

假设变形飞行器无动力飞行，地球为一均质圆球，同时忽略地球自转，则合外力只包含气动力、重力项，合外力矩只包含气动力矩项。同时假设不考虑飞行器横侧向运动，将变形附加力、附加力矩简化到纵向平面内，可得到具体表达式如下：

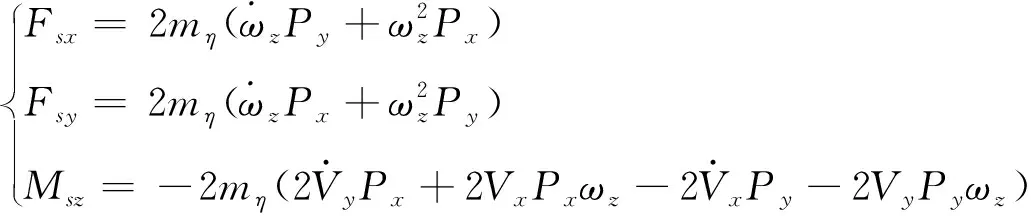
(2)

式中，Fsx和Fsy分别为变形附加力在弹体坐标系xy轴的分量，Msz为变形附加力矩在弹体坐标系z轴的分量，mη为伸缩机翼部分质量，ωz为俯仰角速度，Vx和Vy分别为飞行器运动速度在质心坐标系xy轴的分量，Px和Py分别为机体质心指向伸缩机翼质心矢量在弹体质心坐标系xy轴的分量，随飞行器变形而发生变化。

结合飞行器运动学方程，将多刚体动力学模型转换到速度坐标系中，可得到变形飞行器完整数学模型，如式(3)。

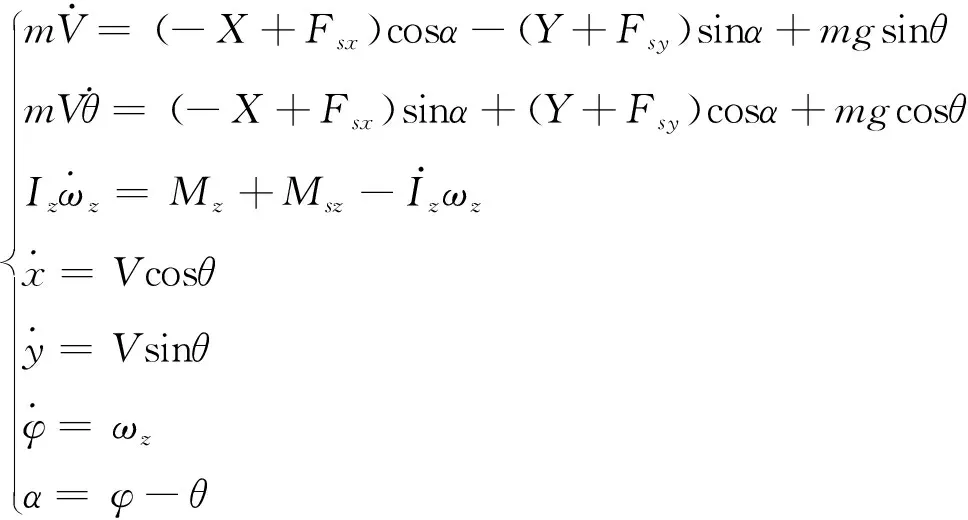
(3)

式中,V和θ分别为飞行器飞行总速度、速度倾角，α为攻角，g为当地重力加速度，Iz为飞行器绕z轴转动惯量，φ为俯仰角，x和y分别为飞行器在发射坐标系xy轴的位置，X，Y和Mz分别为飞行器所受气动力、力矩在质心坐标系三轴的分量，表达式如式(4)。

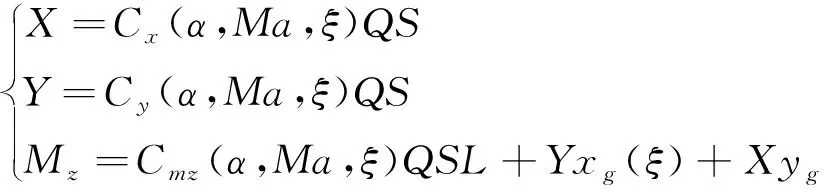
(4)

式中，Q=0.5ρV2为动压，S和L分别为飞行器参考面积、参考长度，xg和yg分别为飞行器质心到理论顶点的距离在xy轴的分量，随飞行器变形而发生变化，Cx，Cy和Cmz分别为轴向力系数、法向力系数、俯仰力矩系数，其大小与攻角、马赫数以及机翼变形量有关。

2 基于深度强化学习算法的控制设计

2.1 深度强化学习算法原理

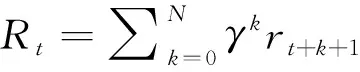
本文采用的TD3算法是一种基于“动作-评价”(Actor-Critic, AC)框架的深度强化学习算法，采用深度神经网络表征策略π和动作-值函数Qπ(s,act)=Ετ～π[R(τ)|s,act]。其在DDPG的基础上改进得到，采用Double Q-Learning的方式降低Q值估计误差，通过延迟策略更新的方式来增加算法的稳定性，并且在目标策略中加入噪声来避免过拟合，进一步提升了算法稳定性与收敛性，是目前应用较为广泛的一类连续控制强化学习算法。

TD3一般使用6个神经网络：策略网络及策略目标网络、2个评价网络及2个评价目标网络，策略网络用来表征确定性策略π(s|θπ)，其中θπ为网络参数，2个评价网络分别用来表征2套动作-值函数Q1(s,act|θQ1)和Q2(s,act|θQ2)，θQ1和θQ2分别为对应的网络参数，同样对应2个评价目标网络Q1′(s,act|θQ1′)和Q2′(s,act|θQ2′)，θQ1′和θQ2′分别为对应的网络参数，网络更新时选取2个目标网络中最小值，计算时间差分误差(Time Difference error, TD-error)，如式(5)。

δt=rt+1+γmini = 1,2

{Qi′[st+1,π′(st+1|θπ′)|θQi′]}-Qi(st,actt|θQi)

(5)

式中，π′(st+1|θπ′)为策略目标网络输出，θπ′为其网络参数，因此可构造评价网络损失函数及更新方式如式(6)。

(6)

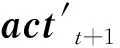
(7)

ν～clip[N(0,σ),-c,c]为截断的高斯噪声，N为批学习的样本数量，κQ为评价网络的学习率。同样可构造策略网络损失函数及更新方式如式(8)。

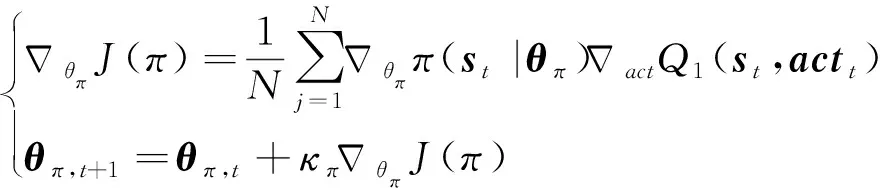
(8)

式中,actt=π(st|θπ)为st状态下智能体输出动作，κπ为动作网络的学习率，TD3算法使得策略网络以更低的频率更新，在评价网络更新d步后再更新策略，以获得更高的更新质量，增强算法稳定性。同时TD3通过指数平滑而非直接替换的方式更新目标网络，如式(9)所示。

(9)

式中,ε为惯性更新率，一般为小于1的正数，可以使得目标网络更新更缓慢平稳，提高训练的稳定性。

2.2 控制设计

前期训练发现利用策略网络直接输出舵偏角指令的控制器架构在训练时存在大量无法稳定飞行，状态发散的现象，导致训练效率降低，同时很难得到最优结果。因此本文加入PD控制器进行辅助，与策略网络组成复合控制器，PD控制器参数粗整定，仅能维持稳定控制，跟踪精度较差，在此基础上利用TD3优化控制策略，控制策略训练结构如图2所示，其中虚线框中为控制器结构，控制指令由基础控制器输出指令以及算法策略网络输出动作组成。

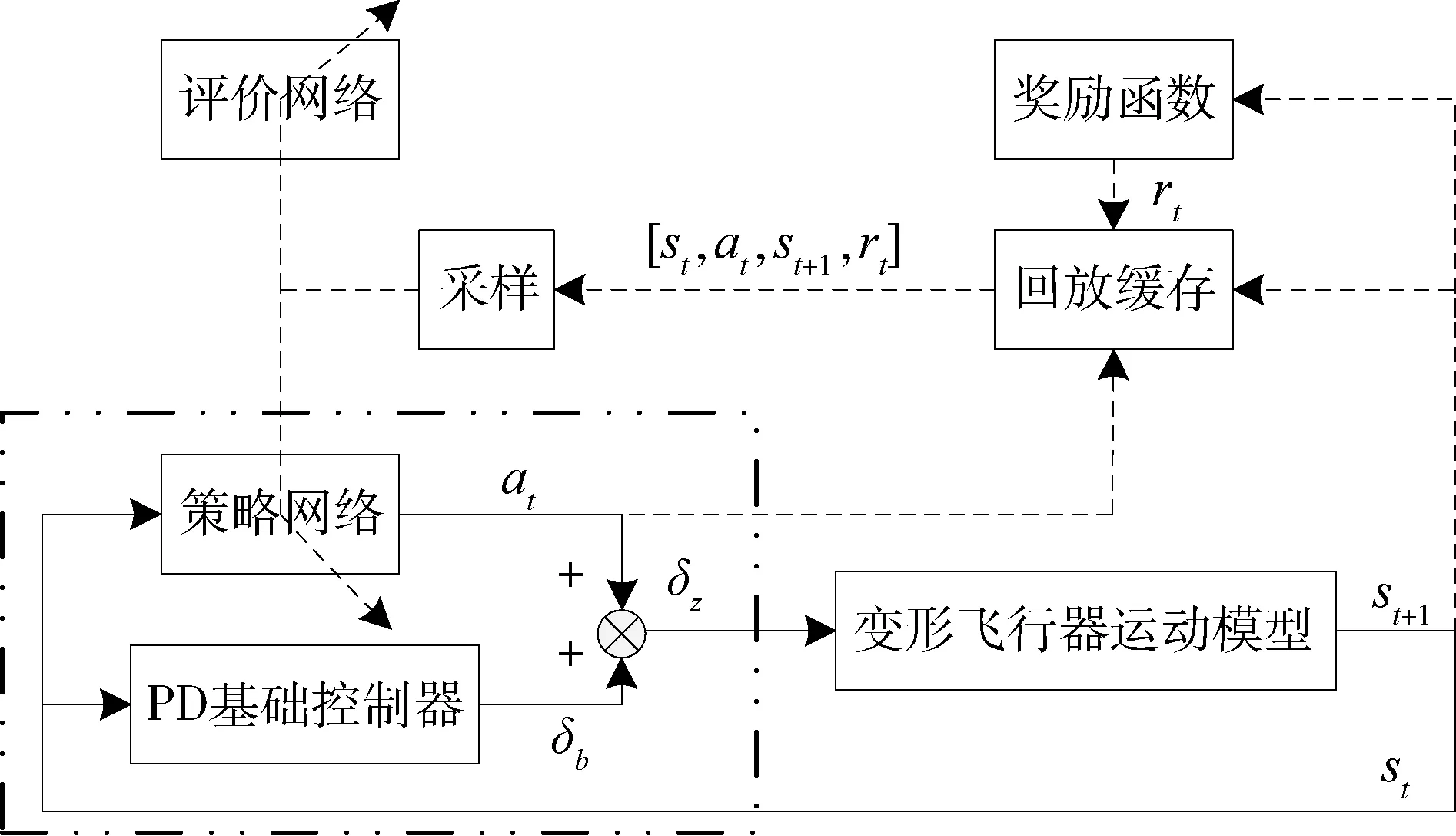
图2 控制器结构图

本文将变形飞行器控制模型转换为MDP，在此框架下设计了状态空间、动作空间、奖励函数以及神经网络结构。

1)状态空间和动作空间

借鉴传统控制器设计思路，影响控制指令的主要因素包含姿态角误差、姿态角速率，同时考虑影响变形飞行器控制律设计的主要因素包含攻角、动压以及变形量。因此选择状态空间为6维向量，由攻角α、攻角跟踪误差Δα、俯仰角速率ωz、舵偏角δz、动压Q、变形率ξ组成，同时为弥补由于评价网络对动作-值函数估计不准确导致训练结果存在明显稳态误差的问题，借鉴PID控制引入积分项的思路，在状态量中引入攻角跟踪误差的历史信息，即Iα=Δα+μIα，最终设计状态向量如下：

s=[α,Iα,ωz,δz,Q,ξ]

(10)

考虑控制系统执行机构仅有气动舵，纵向平面控制指令仅含俯仰舵偏，因此动作空间设计为1维向量，如式(11)。

act=δz

(11)

2)奖励函数

为保证变形飞行器姿态跟踪精度，为变形创造良好的作动环境，同时降低姿态控制能量需求，设计奖励函数由跟踪误差惩罚、舵偏角大小惩罚以及跟踪精度稀疏回报组成，如式(12)。

(12)

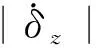
3)深度神经网络结构

本文采用的神经网络均为反向传播(Back Propagation, BP)神经网络，动作网络输入层有6个神经元对应6维状态向量st，隐藏层为3个全连接层，输出层有1个神经元对应1维动作向量actt。两个评价网络结构相同，输入层有7个神经元对应6维状态向量st和1维动作向量actt，隐藏层同样为3个全连接层，输出层有1个神经元对应动作-值函数Qi(st,actt|θQi)，各层神经元数目与激活函数如表1，目标网络与对应网络结构相同。

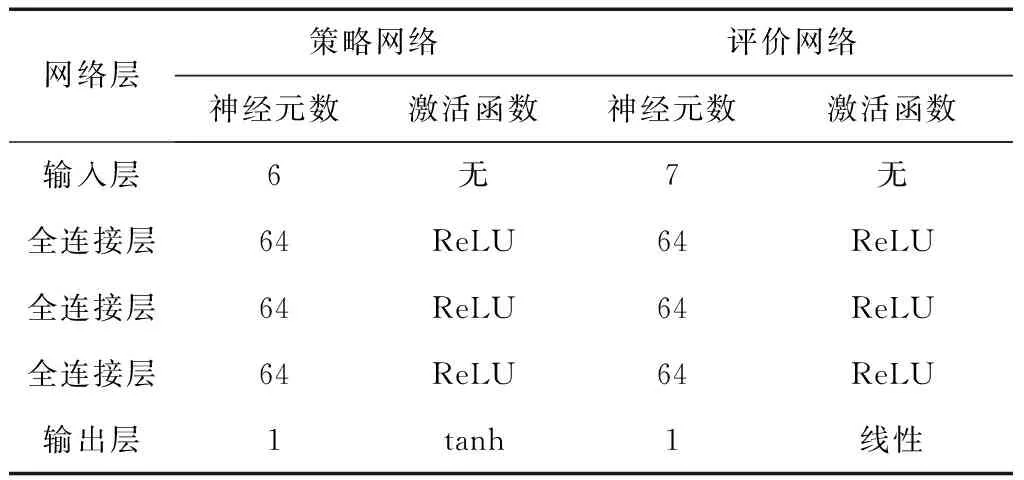
表1 神经网络结构

3 仿真分析

3.1 TD3算法训练

1)训练场景

仿真开始时伸缩机翼处于伸展状态，其可以在1.25s内匀速收回至本体状态，变形指令设置如图3，7.5s开始伸缩机翼逐渐收回，12s再次展开，16.5s伸缩机翼再次收回，最终21s伸缩翼展开到初始状态。

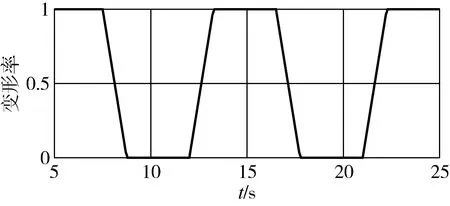
图3 变形率变化曲线

TD3算法训练中积分周期为5ms，控制周期为10ms，网络更新周期为50ms，每回合仿真总时长30s，算法训练参数以及奖励函数权重设计如表2所示。

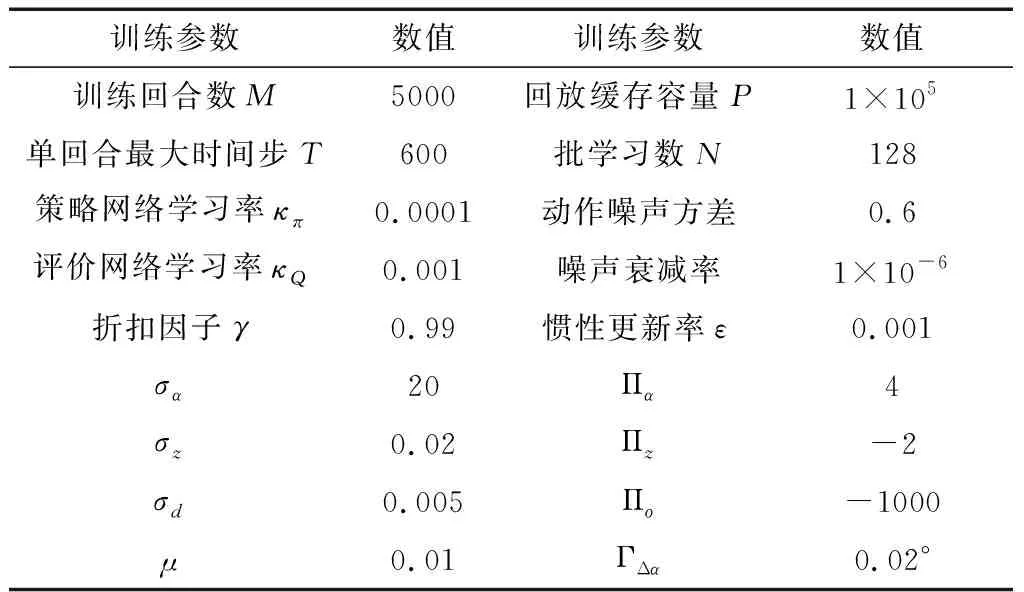
表2 算法训练参数设计

为得到鲁棒性更强的控制策略，在训练中加入初始状态偏差以及随机干扰项，扰动水平如表3所示。

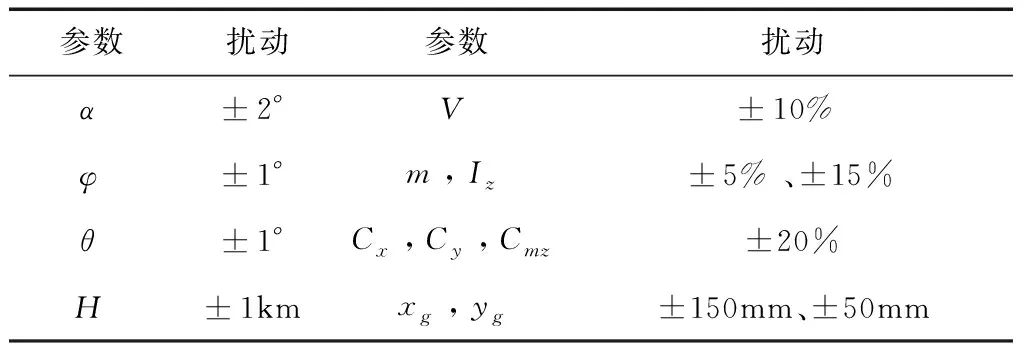
表3 扰动参数及扰动水平

并做出以下假设：

假设1：飞行器无横侧向运动，仅在纵向平面运动；

假设2：仿真中假设传感器无测量误差，执行机构无惯性，仅考虑气动偏差、结构偏差等设计误差以及风干扰等外界环境影响。

2)训练结果

基于变形飞行器纵向平面动力学模型，分别基于TD3以及DDPG算法开展控制策略训练，图4展示了训练过程平均奖励随训练回合的变化规律，共进行了5000回合训练，每10回合取平均值，其中蓝色实线为TD3算法训练结果，黑色虚线为DDPG算法训练结果，在训练初期智能体处于探索阶段，累计奖励存在降低趋势，当进行到100回合后，累计奖励明显增加，直到1000回合左右逐渐趋于稳定，对比可以发现TD3算法比DDPG算法具有更好的稳定性以及更快的收敛速度，训练所得的控制策略累计奖励也达到了更高水平。

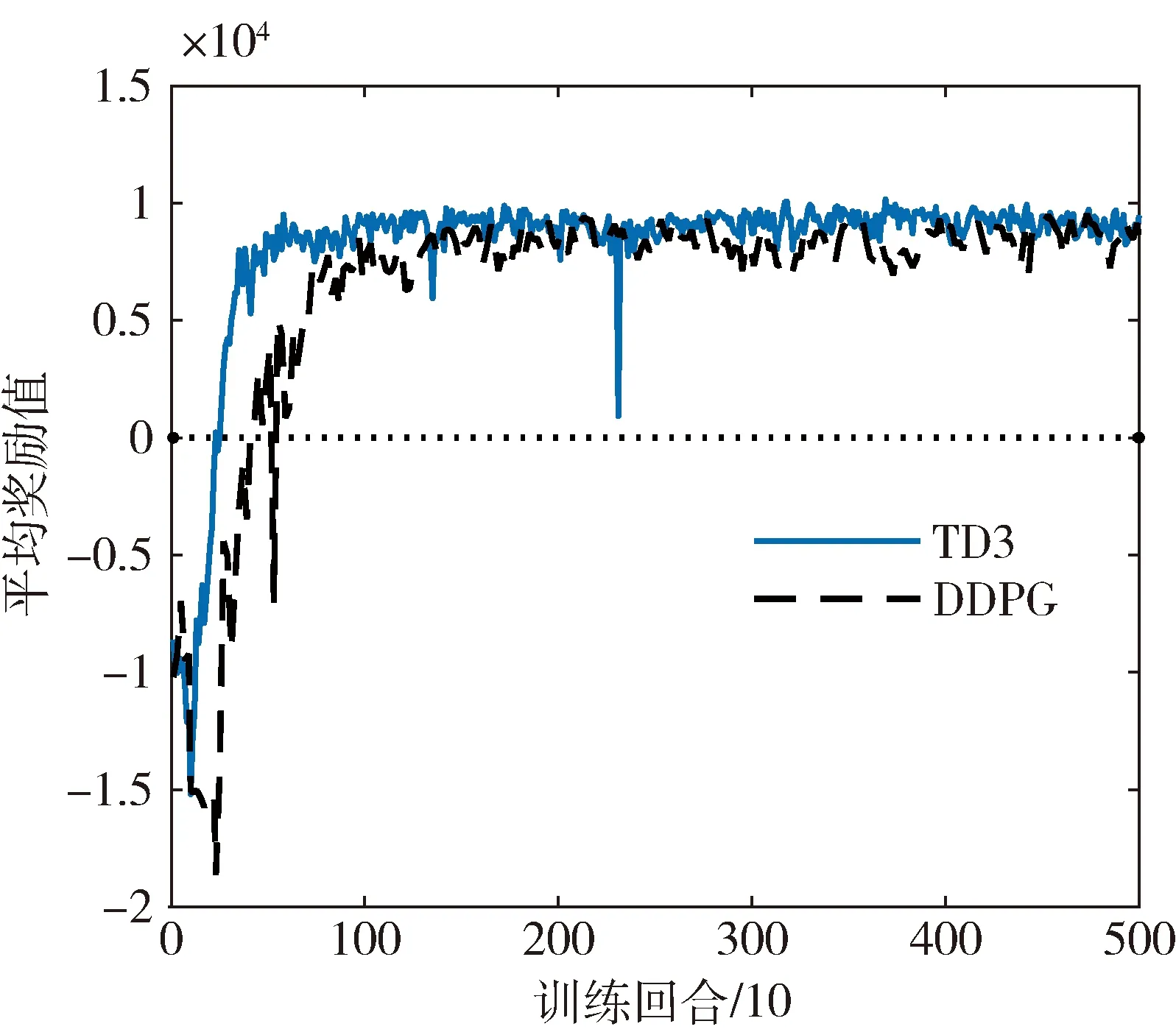
图4 训练过程平均奖励变化曲线

3.2 变形飞行器姿态控制仿真验证

为验证控制策略的有效性，本文共开展了3组数学仿真，分别为标称状态下的仿真验证、偏差状态下的仿真验证以及改变变形指令的仿真验证。

3.2.1 标称状态仿真验证

图5～6展示了标称状态下的攻角跟踪结果以及俯仰角速率、舵偏角响应结果，攻角跟踪梯形指令，在-5 °攻角进行连续变形测试，并将仿真结果与基础PD控制器以及PID控制器的控制效果进行对比。

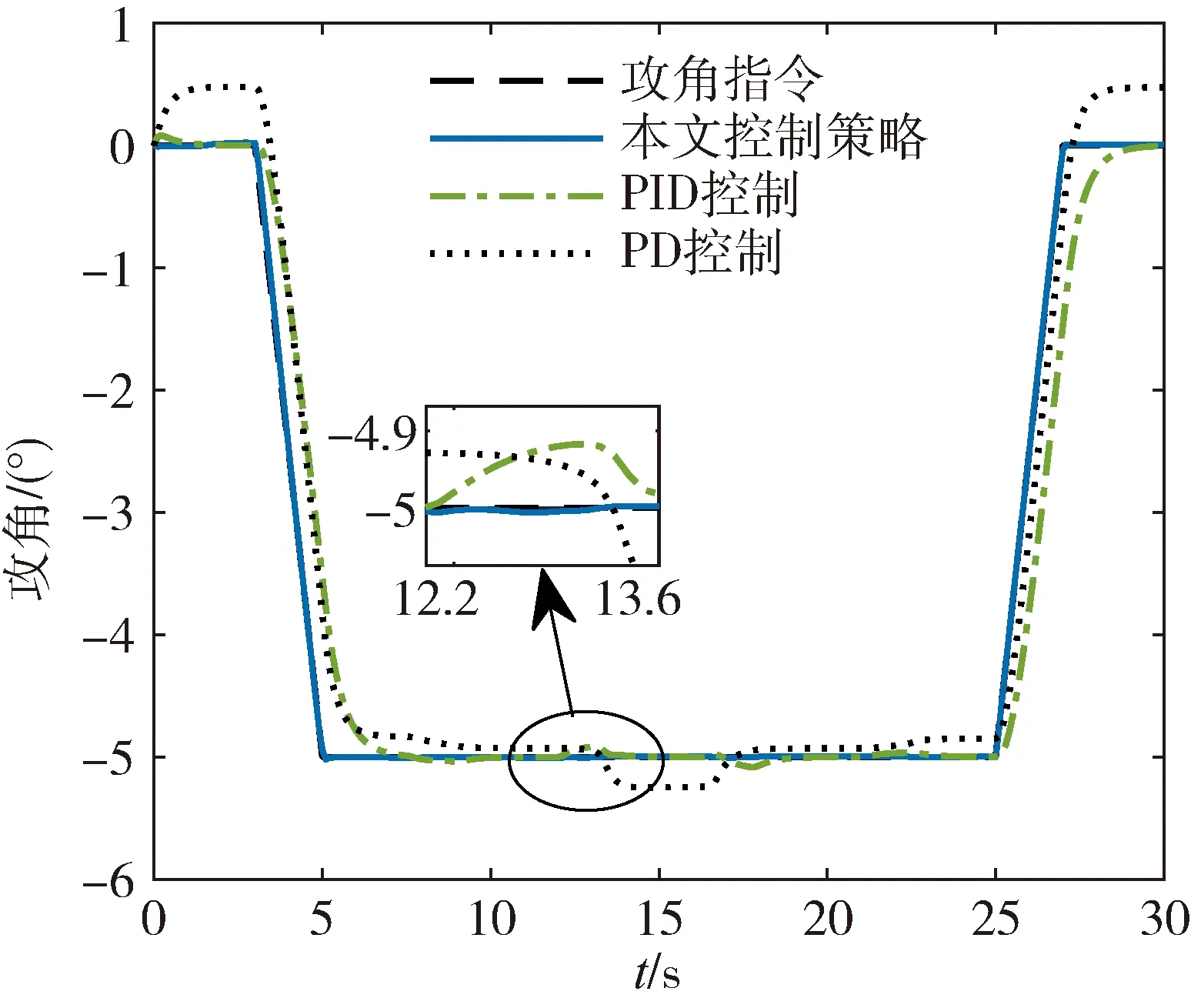
图5 攻角跟踪

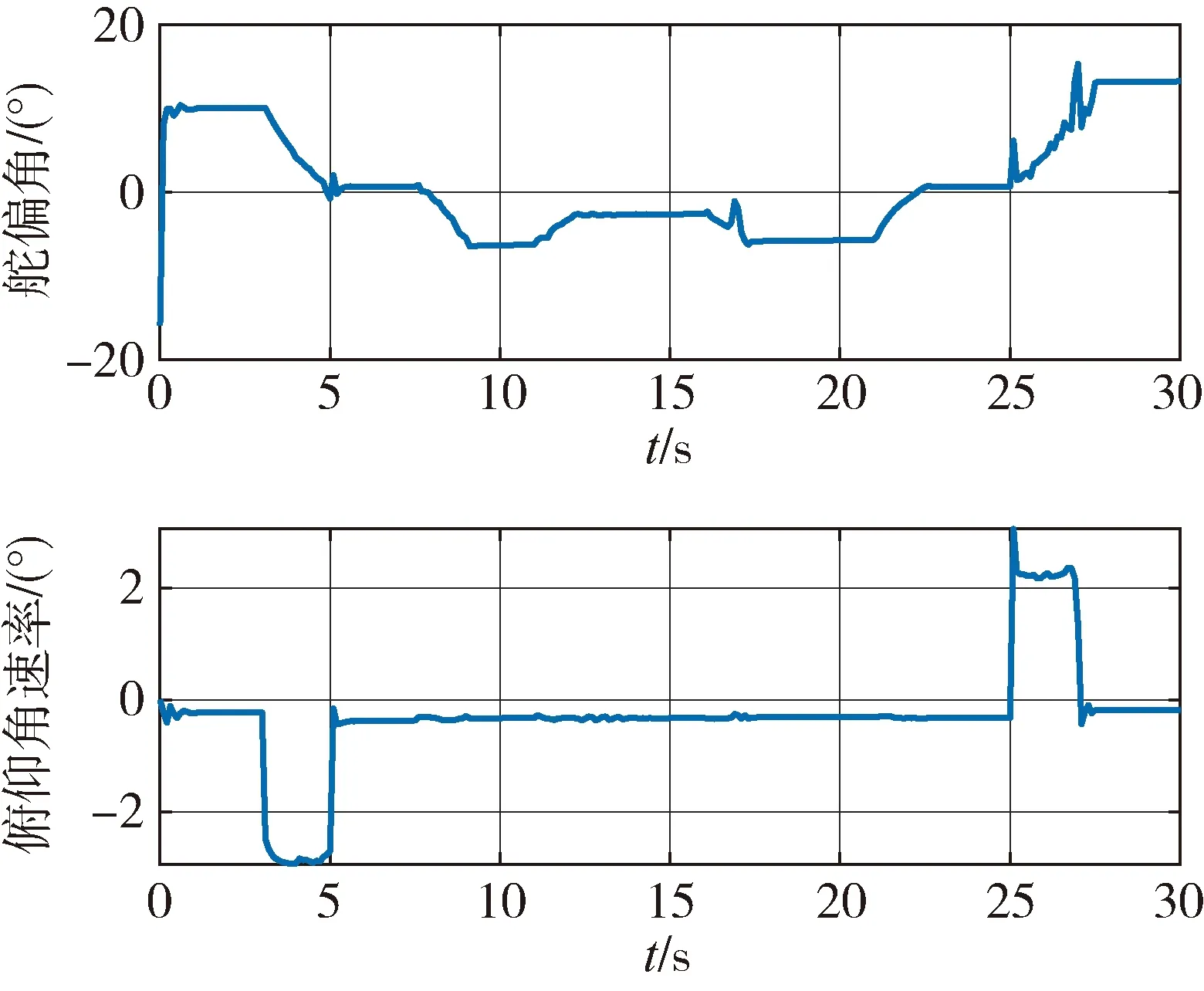
图6 俯仰角速率、舵偏角响应

表4展示了TD3与PD基础控制器、PID控制器控制效果的对比，其中积分绝对误差IAE(Integral Absolute Error)为攻角跟踪误差随时间的积分项。

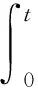
(13)

表4 控制效果对比

仿真结果表明本文经TD3算法训练后的控制策略可以实现动态、稳态的高精度控制，相较于基础控制器具有更快的响应速度、更小的稳态误差，从而为飞行器变形提供良好的初始状态。相较于性能更优的PID控制，本文的控制策略在变形过程中攻角跟踪误差无明显变化，可以快速适应飞行器变形引起的模型变化，对变形引起的模型内部不确定性具有较强的鲁棒性，可以实现机翼伸缩变形条件下的攻角指令精确跟踪。

3.2.2 偏差状态仿真验证

为验证本文控制策略对变形过程中复杂外界干扰的鲁棒性，考虑初始状态偏差以及气动、结构、环境干扰偏差，扰动项及扰动水平如表2所示，取极限拉偏组合，同时加入大气环境干扰，包含大气密度偏差、温度偏差、风干扰。基于随机组合开展1000条蒙特卡洛仿真，图7～8展示了攻角跟踪结果以及1000次仿真中跟踪误差频率分布。

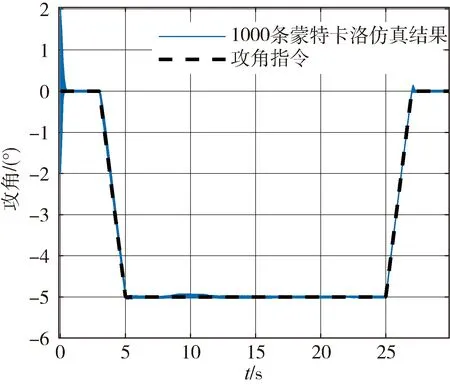
图7 攻角蒙特卡洛仿真结果

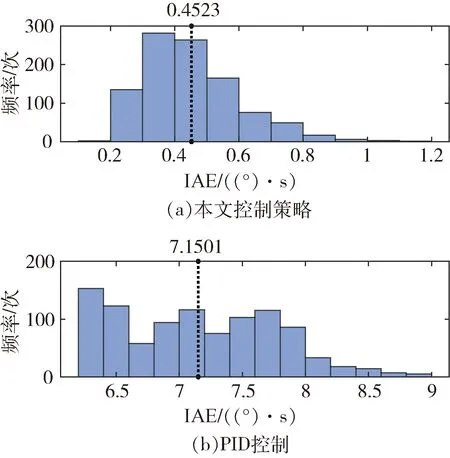
图8 攻角跟踪误差频率分布

观察结果发现，1000次蒙特卡洛仿真均可以实现姿态稳定控制，IAE平均值为0.4523((°)·s)，分布方差为0.1492，与PID控制1000次蒙特卡洛仿真IAE平均值7.1501((°)·s)，分布方差0.6199进行对比，优化后的控制策略精度更高，蒙特卡洛仿真分布方差更小，证明了其对初始状态、设计偏差以及环境等外部干扰项的鲁棒性更强，由此验证了本文控制策略对变形飞行器系统内部、外部不确定性均具有较强的鲁棒性。

3.2.3 未经训练的变形指令仿真验证

本文在训练中只考虑了单一变形策略，为验证网络泛化能力，测试其对变形策略在线决策场景的适应能力，考虑攻角-5 °的状态下，在10s～20s之间随机给定50种伸缩机翼变形指令，在标称状态下开展仿真，攻角跟踪结果以及俯仰角速率、舵偏角响应结果如图9～10所示。

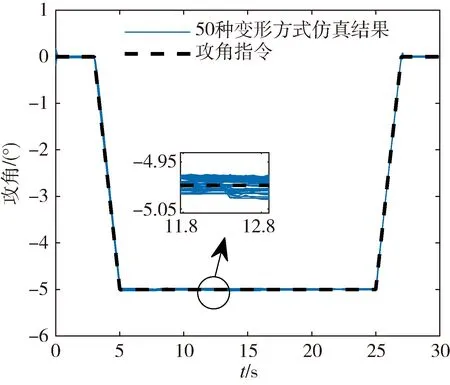
图9 攻角跟踪曲线

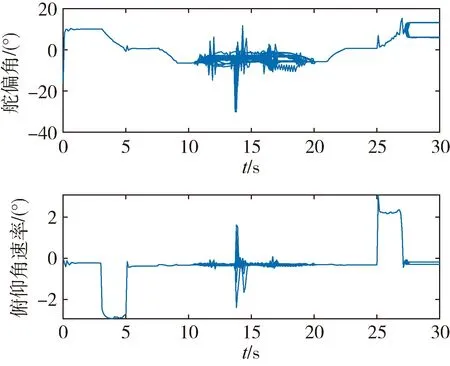
图10 俯仰角速率、舵偏角响应

仿真结果表明，50次测试均能实现变形过程中的姿态稳定控制，IAE平均值为0.4058((°)·s)，证明本文的控制策略对未经训练的变形指令具有一定的适应性，可以实现在线灵活变形场景下的高精度姿态控制，体现了算法较强的泛化能力，同时由于本节仿真中的变形指令并未参与算法训练，需用舵偏量未经过优化，变形过程中俯仰角速率和舵偏角存在小幅度振荡现象，并未影响控制系统稳定性以及控制精度。

4 结论

针对变形飞行器动力学模型非线性强，变形过程中内外干扰因素复杂，以及灵活变形引起的模型大范围变化的问题，以一类机翼可伸缩的变形飞行器为例，基于TD3深度强化学习算法开展了变形飞行器姿态控制算法设计，获得了较DDPG算法更好的训练效果，同时本文采用PD控制器辅助TD3算法训练的方式，保证算法训练初期的稳定控制，提升样本质量，并采用攻角跟踪误差的累加值作为状态输入，进一步提升训练效果，降低控制策略稳态误差。仿真结果表明本文的控制策略可以保证机翼伸缩变形过程中姿态控制的精度，对模型内外不确定性均具有较强的鲁棒性，同时对不同变形策略具有一定的适应性。