机器学习算法在济南泉群水位流量预测中的应用

于询鹏，仇东山，曹美

（1.济南市水文中心，山东 济南 250014；2.济南众联电子科技有限公司，山东 济南 250100）

济南城区泉水喷涌点主要包含趵突泉泉群、黑虎泉泉群、五龙潭泉群、珍珠泉泉群四大泉群，泉水可持续喷涌是济南作为旅游城市以及生态文明城市建设重要的体现。济南市水文中心自2010 年承担济南市四大泉群水位流量监测任务，目前已积累了大量的泉水监测数据。文章利用机器学习方法对四大泉群水位流量进行回归分析，并评价分析多种算法对回归数据的可靠性和准确性，以得出最优的回归方程式，便于进行泉群出水量的预测。

目前机器学习算法主要包括有监督学习、无监督学习。前者主要应用在分类和回归任务，后者主要应用在聚类任务，针对泉群地下水位和流量回归分析属于典型的有监督学习。目前，传统的水文流量推算是根据实测水位流量数据进行简单的曲线拟合，但拟合精度较差，通过机器学习可极大提高拟合精度和效率。本文分别通过机器学习的线性回归、梯度下降、岭回归、水文模型等算法对历史样本数据进行分析，并比较各算法预测成果的优劣。

数据分析平台采用Python 编程语言，开发环境采用Anaconda Jupyter notebook，机器算法使用Scikit-learn（sklearn）、Numpy 和Pandas 等分析库，图形库选用Seaborn、matplotlib。

1 四大泉群水位流量样本采集与分析

1.1 样本采集

自2010 年开始进行四大泉群的流量监测，所有样本数据选用2010—2021 年12 年的监测数据，实测水位流量数据期间的趵突泉地下水位选用济南城乡水务局趵突泉地下水位观测井遥测数据，样本数据采集曲线见图1、图2。

图1 趵突泉、黑虎泉地下水位数据

图2 趵突泉地下水位与泉群日流量实测数据

由图1、图2 可知，水位数据分别在高中低水位都有分布，样本数据选择合理，实测流量数据与趵突泉地下水位呈明显的线性分布。本次趵突泉、黑虎泉地下水位数据样本量4 320个，实测流量数据样本量544个，趵突泉地下水位分布区间27.16～30.18 m，平均水位28.30 m，黑虎泉地下水位分布区间27.12～30.46 m，平均水位28.27 m，四大泉群总出水流量数据分布区间0.14～4.59 m3/s，日出水量分别为1.24～39.6 万m3，平均日出水量16.3 万m3。

1.2 相关性分析

从实测数据样本中分别选取趵突泉地下水位和泉群总出水流量作为相关性分析变量，使用Seaborn 库中的API 函数regplot 进行相关分析，见图3。

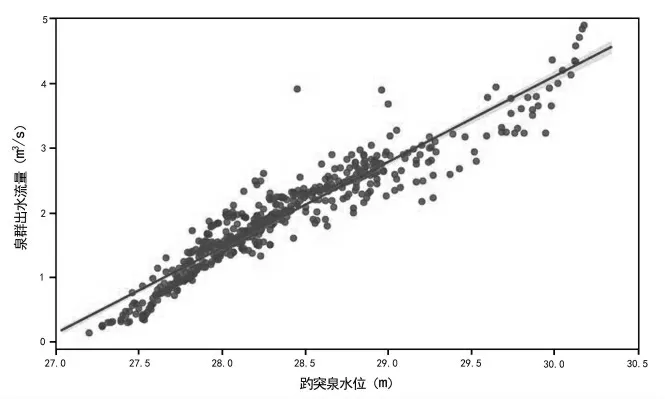
图3 趵突泉水位与泉群出水流量实测数据

通过计算可知，趵突泉水位与泉群流量相关系数为0.952 6，趵突泉水位与黑虎泉水位相关系数为0.966 8。从样本数据散点图和相关性计算结果可以看出趵突泉地下水位与泉群流量以及趵突泉与黑虎泉具有高度正相关性，两者的相关系数分别达到0.95 和0.96 以上，可以进行回归预测分析。

2 趵突泉水位和泉群流量线性回归分析

2.1 数据清洗和整理

整合自2010 年7 月至2021 年10 月之间所有的实测数据，根据实测日期读取相同日期对应的趵突泉地下水位，分别计算每个测次泉群各个出水断面出水流量，合计为四大泉群总出水流量，个别缺测断面数据使用相同水位下的实测值填充，样本数据整合结果见表1。

表1 样本数据整合结果表 m3/s

2.2 回归分析及预测成果评价

假设趵突泉地下水位与泉群总出水流量的线性方程为y=β0+β1x+ε，其中x 为因变量趵突泉水位，y 为自变量泉群总流量，β0为截距，β1为权重系数，ε 为误差项，实测样本数据利用最小二乘法拟合期望值，使每个实测流量点到拟合直线的离差平方和最小，并通过推导求出β0、β1的估计值，方程式如下：

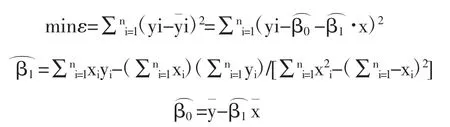
分别从sklearn 库中导入回归分析所用的函数库，并使用sklearn 库中的函数对拟合直线进行MSE（均方差）、R-square（确定系数）的计算，以确实各种回归模型的优劣，本数据分析使用以下sklearn 库。

1）划分训练集及测试集：from sklearn.model_selection import train_test_split。

2）数据归一化处理：from sklearn.preprocessing import StandardScaler。

3）线性正规方程：from sklearn.linear_model import LinearRegressio。

4）岭回归：from sklearn.linear_model import Ridge。

5）梯度下降：from sklearn.linear_model import SGDRegressor。

此外，通过把资料整编率定的水文模型lnQ=0.167+1.015 ln（ΔZ）纳入到评估体系中，其中ΔZ为因变量，是泉群断流趵突泉水位线的高程差，初步确定为26.7 m。把实测流量样本数据分割为训练集和测试集，其中测试集分割为总样本数的20%，分别把测试集数据代入到各个回归模型中，并返回回归方程，把测试集数据导入模型预测函数，并生成预测值，最后，把预测值与实测值进行平均误差、MSE（均方差）、R2（确定系数）计算，来评估各个回归模型的拟合效果。各回归模型预测评估结果见表2。

表2 各回归模型预测评估结果表

根据以上各回归模型预测评估结果可以看出，平均误差、均方差、确定系数（R2）都相差不大，但从确定系数（R2）来评估各模型优劣，线性正规方程拟合效果最好，分别用测试集和各模型的预测值进行回归曲线模拟。

其中中高水拟合较好，低水预测值较实测值偏高，主要是因为在低水期各出水断面流量很小，受系统误差、随机误差影响较明显，并且黑虎泉白石桥断面受下游船闸蓄防水影响较大。

根据2010—2021 年趵突泉水位时间序列，同时把水位曲线和根据实测水位预测泉群流量放置在一张图上，见图4，可直观显示各次实测流量与预测流量的比较，整体预测曲线拟合较好。

图4 水位曲线与实测水位预测泉群流量拟合图

3 结语

通过以上数据分析可以得出：趵突泉地下水位与四大泉群总流量具有高度线性相关性。通过机器学习对原始实测资料回归分析，计算出趵突泉水位和泉群流量的线性方程式，模型库可在实际工作中通过数据接口实时读取远端数据库趵突泉地下水位信息，快捷高效计算出泉群出水流量，便于水位流量预测分析以及泉水利用。此外，随着高中低水位实测流量频次的不断增加，可实时导入进预测分析模型，逐步提高回归模型预测准确度。