基于ISSA-GRNN的无线传感器网络定位优化算法

王家威,薛亚辉,魏子尧

1.焦作大学 信息工程学院,河南 焦作 454000;2.中国石油大学(华东) 控制科学与工程学院,山东 青岛 266580

随着信息与网络技术的不断发展,无线传感器网络(Wireless Sensor Network,WSN)作为一项重要技术也已广泛应用于追踪、探测等领域[1-2]。节点定位问题作为其重点处理的问题之一,这些年来也在不断改进和更新。经典的无线传感器网络定位算法主要包括基于TOA、AOA、RSSI等距离相关算法[3]和基于Centroid、DV-Hop、APIT等距离无关这两大类算法[4-6]。

近年来,智能优化算法的不断出现和深入融合促进了诸多技术与领域的协同发展,在定位问题上,也得到较多的应用。范时平等[7]DV-Hop算法的节点跳距进行改进,并与粒子群算法结合进行传感器节点定位;方旺盛等[8]在改进粒子群算法优化的基础上,对节点跳数、跳距进行修正;印雷等[9]提出了改进的麻雀搜索算法,并对修正后的DV-Hop算法进行优化;颜慧超等[10]提出了一种ISSA-DH算法,主要改进了节点跳数、跳距以及位置的计算方法;高栋等[11]利用RSSI修正Centroid算法的质心,并结合灰狼优化算法对相关节点进行定位。

针对DV-Hop和Centroid算法的定位精度问题,本文将这两种算法和加权优化方法进行融合。利用加权平均法,通过预估距离与实际距离之间的误差量修正跳距,利用改进的加权因子并引入RSSI修正Centroid算法的质心。通过采集不同节点间的关联特征,将修正后的跳距特征、质心特征和节点其他重要特征等进行特征融合,添加到广义回归神经网络(generalized regression neural network,GRNN)[12]中进行训练。在结合GRNN的同时,需要考虑网络中的调节参数对整体效果的影响,本文利用麻雀搜索算法(sparrow search algorithm,SSA)[13-14]的优化思想改善GRNN网络参数,以解决参数随机设置而导致预测不准确的问题。仿真实验结果表明,结合后的优化算法可以有效减少定位误差,提高节点定位精度。

1 相关算法理论

1.1 WSN定位算法

1.1.1 DV-Hop定位算法

DV-Hop算法作为WSN中一种经典的分布式定位方法,主要由以下几个定位阶段组成。首先,锚节点借助泛洪广播向网络中的其他节点发送自身节点的位置和跳数等信息,泛洪广播完成后,每一个节点会获取到与锚节点的最小跳数。当每个锚节点均接收到与所有其他锚节点间的距离和跳数信息时,需要计算锚节点间的平均跳距hopsize。未知节点k到锚节点i间的距离dk,i则根据锚节点的平均跳距hopsizek与最小跳数hk,i的乘积来计算,并使用最小二乘法来估计未知节点的坐标。

1.1.2 Centroid定位算法

Centroid定位算法主要通过求解多边形的质心来确定未知节点的位置,确定质心的方法如下:假设某区域内一共存在M个节点,其中锚节点有N个,未知节点有(M-N)个,M个节点的位置用坐标(xi,yi)表示,其中,i∈(0,1,…,M)。在通信半径能够辐射的范围内,各锚节点周期性地向周围其他节点广播含自身位置的分组信息,当某节点接收到一定量信息后,计算由接收到的锚节点组成的多边形的质心,并用坐标表示,完成Centroid定位。

1.2 广义回归神经网络

广义回归神经网络(GRNN)属于径向基函数网络的一种改进模型,在非线性回归分析领域有很强的数据处理能力。它的结构模型主要包括输入层、模式层、求和层以及输出层这四层。如图1所示,输入层向量X=[x1,x2,…,xm]Τ,输出层向量Y=[y1,y2,…,yn]Τ,不同层的各个节点之间都有相应的网络参数连接。GRNN具有和径向基函数网络相似的输入层与模式层,模式层包含多个神经元,其数量和学习样本量相同。在求和层中含有两类不同功能的神经元,作用分别是对模式层中神经元的输出进行算术求和以及加权求和。GRNN复杂的神经网状结构具有比径向基函数网络更好的运算速度和预测效果。

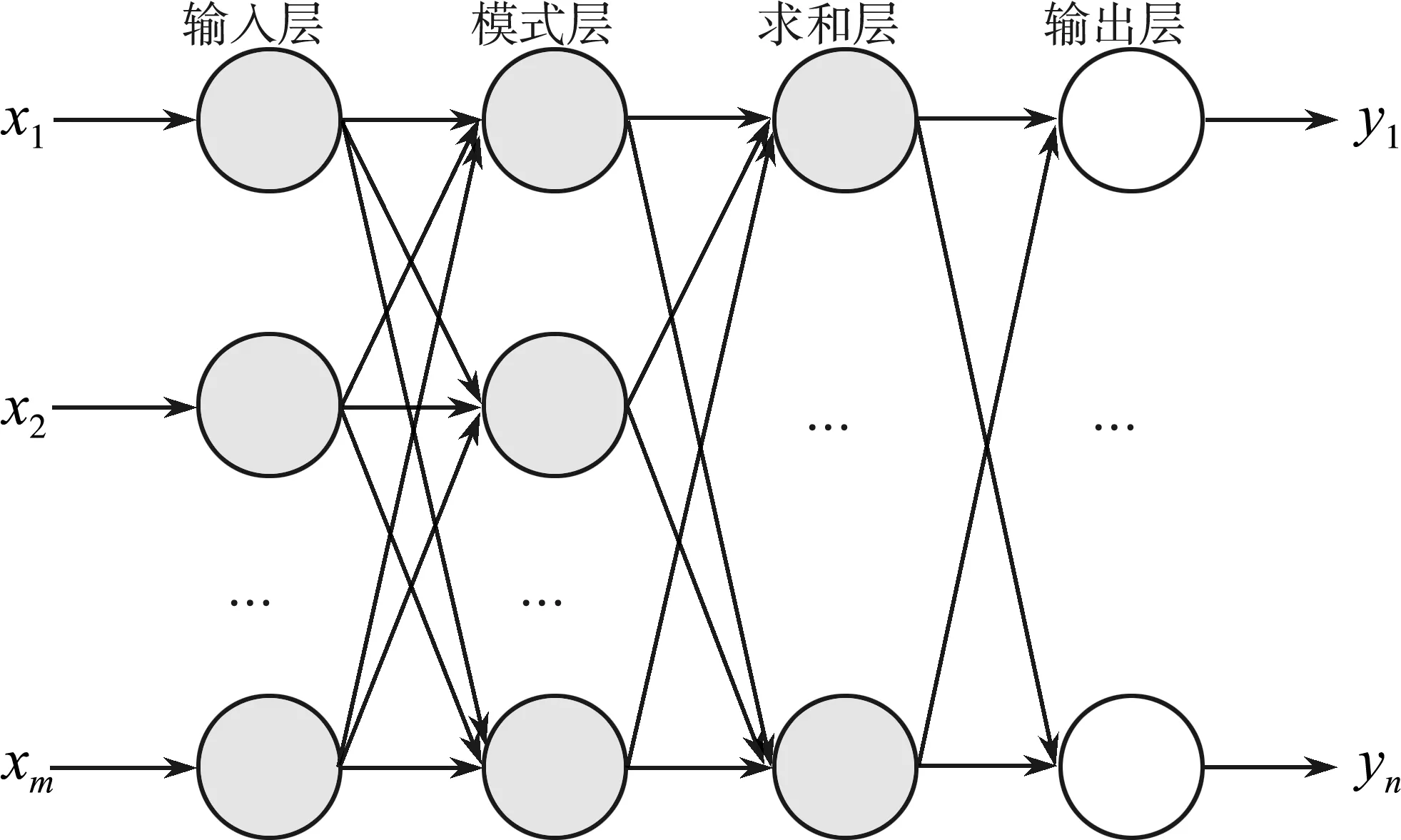
图1 GRNN结构模型

在GRNN模式层中,神经元之间的传输函数Pi可以用式(1)表示:

其中,X表示输入变量;Xi表示第i个神经元指向的学习样本;σ表示光滑因子;i=1,2,…,m。

经过GRNN求和层中两类求和方法求解后,在输出层利用求和结果相除的方法输出预估结果的第j个元素yj,具体见式(2):

其中,yij表示连接权值,对应于第i个输出样本Yi中第j个数值;j=1,2,…,n。

1.3 麻雀搜索算法

麻雀搜索算法(SSA)最早于2020年提出,是一种较新的智能优化算法。该算法是从麻雀这种鸟类的觅食、反捕食活动中获得的灵感,该算法中的种群,是由搜寻者和跟随者组成,通过搜寻者不断寻觅食物,逐渐指引跟随者前进,算法的寻优效果好,收敛速度快。

假设一个麻雀种群包含n只麻雀,觅食空间大小为d维,在搜寻者寻觅食物的过程中,其位置也在不断更新,具体更新方法见式(3):

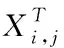
跟随者的位置更新方法见式(4):

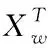
SSA需要选择10%～20%的麻雀来勘察预警,以便随时进行反捕食活动,从而保证麻雀种群的安全。预警者的位置更新方法见式(5):

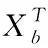
2 本文优化方法

本文的优化方法主要从两个方面展开,分别是对传统定位方法的改进和使用优化的神经网络预测节点的最终位置。将DV-Hop和Centroid这两种算法和加权定位求解思想进行融合,修正DV-Hop算法的跳距和Centroid算法的质心等信息,把节点融合特征引入GRNN中进行网络训练,并利用改进的SSA优化GRNN进行定位,以更大程度地减少定位误差。

2.1 平均跳距修正

在传统的DV-Hop定位算法中,通常使用锚节点坐标间的欧氏距离与最小跳数的商计算平均跳距,使得最终预测的节点位置误差较大。本文利用加权平均思想,结合文献[9]和文献[10]提出的方法修正跳距,以综合考虑节点平均跳距对定位精度的影响。

假设锚节点个数为n,根据最小均方误差原则,锚节点i的平均跳距hopsizei的计算方式如下:

其中,hopij表示锚节点间最小跳数;dij表示锚节点间的距离。

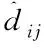
跳距校正系数εi则根据锚节点间的估算距离和实际距离的差值与跳数进行相应计算得到,具体可按式(8)计算:

那么,经修正后的锚节点平均跳距可表示为:

对于未知节点而言,在计算平均跳距时,通过添入加权因子来修正跳距权重:

其中,hopi和hopj表示单个锚节点i、全部锚节点(j=1,2,…,n)分别和未知节点间的跳数。

2.2 质心修正

为了解决传统Centroid定位方法存在的误差,通过获取节点接收的RSSI信号强度指示这一重要指标,进而对质心进行修正。

RSSI具有操作方便、 通信损耗较少等优点,信号发送方i和接收方j之间的RSSI值Pdij满足关系式:

其中,dij表示信号发送方、接收方间的端距;d0表示信号参考距离;n表示路径衰减指数;Xσ表示随机分布的高斯噪声。

传统的三角形Centroid定位方法原理如下:假设三个锚节点坐标分别为A1(x1,y1)、A2(x2,y2)、A3(x3,y3),未知节点坐标为O(x,y),以三个锚节点位置为圆心,对应距离为半径,形成三个圆及其重叠部分。连接重叠部分的三个交点O1(xo1,yo1)、O2(xo2,yo2)、O3(xo3,yo3),形成一个三角形,计算该三角形的质心坐标M1(xm1,ym1)即可,如式(12)所示。

文献[11]提出的改进加权Centroid定位方法能够有效提升定位精度。在定位之前,首先对节点收到的RSSI值预处理,本文采用高斯滤波平滑处理RSSI值,并作为新的RSSI值估测锚节点与未知节点的距离,相比于文献[11]采用的中值滤波处理误差更小。

未知节点在收到新的预处理RSSI值后,需要对RSSI值计算得到的距离进行升序排序,取排序前三的距离来选择合适的锚节点,并引入差分修正因子α,如式(13)所示。

其中,N表示与未知节点同在通信范围中的锚节点个数;di表示锚节点和未知节点的间距;d1i表示锚节点和质心的间距。

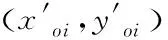
2.3 ISSA-GRNN算法

2.3.1 拉丁超立方体初始化种群

运行SSA算法时,对麻雀种群初始化是必不可少的。通常情况下,会采取随机产生种群的方式初始化,这样可能导致无法充分覆盖解空间,从而影响种群个体分布均匀程度和收敛效果等。采用拉丁超立方体抽样(latin hypercube sampling,LHS)[15]初始化SSA种群,在执行LHS过程时,需要确定一个抽样规模,将每一维的变量分割成多个同等小区间,将大超立方体变为小超立方体。之后,产生一个全排列的矩阵,并最终进行采样。通过整体空间覆盖及抽样非重叠,以提升SSA的种群多样性和寻优性能。

2.3.2 交叉验证法处理网络向量

在运行GRNN模型时,采用交叉验证法(Cross Validation)[16]验证网络算法的性能,将GRNN的网络向量值按组划分,形成训练集及其测试集以多次训练和评估算法模型。在仿真实验中,网络向量值对应于传感器中的不同节点信息,最终使预测模型更有效、更精确。交叉验证过程图2所示。

图2 交叉验证过程

2.3.3 ISSA-GRNN算法流程

为了尽可能消除GRNN初始网络调节参数对定位实验的影响,不断提高定位精度,提出的基于ISSA和GRNN的节点特征融合定位优化方法步骤如下:

(1)初始化WSN环境,确定网络区域,布置网络节点。利用加权定位思想修正DV-Hop算法中的跳距和Centroid算法中的质心等特征。

(2)建立GRNN网络模型,对GRNN中的网络调节参数进行编码,其编码长度作为SSA种群大小。

(3)使用LHS初始化种群,对种群规模、迭代次数等参数进行设定,并生成适应度函数。

(4)将传感器节点修正后的跳距、质心等特征和节点其他重要特征相融合,作为GRNN的输入向量进行训练、测试,节点真实坐标作为训练、测试的输出值。

(5)对SSA的适应度值排序,得到当前最佳个体位置以及最差个体位置。

(6)迭代更新种群位置、适应度值,保存更新后的种群信息。

(7)判断是否达到SSA的终止条件,若达到,则输出最优解,转到(8),否则转到(6)。

(8)解码最优解,并作为更新后GRNN中的网络调节参数。

(9)重新训练、测试GRNN,最终得到未知节点的预测坐标。

3 实验仿真与分析

使用Matlab仿真软件进行算法实验,综合比较了ISSA-GRNN算法与改进跳距的IDV-HOP算法、文献[8]的RDV-HOP算法和文献[9]的ISSADV-HOP算法。定位实验模拟了一个100 m×100 m的区域,该区域随机分布着若干个锚节点和未知节点,锚节点数量占比的设置范围为10%～35%,总节点个数的设置范围为50～300,通信半径的设置范围为20～45 m。SSA的麻雀种群个数为100,迭代次数为200。采用如下方法量化未知节点定位误差:

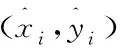
3.1 通信半径对节点定位的影响

图3为不同定位算法在通信半径的影响下其定位误差的对比情况。设置总节点数为100、锚节点数为30,通信半径不断改变。伴随通信半径不断增加,受到锚节点平均跳距产生的影响,使得各算法的整体定位误差在逐渐减小并趋于平稳。由表1可知,ISSA-GRNN算法的平均定位误差相比于其他三种算法分别减少了70.2%、64.5%和26.4%。

图3 通信半径对节点定位的影响

表1 通信半径影响下的平均定位误差对比

3.2 锚节点数对节点定位的影响

图4为不同定位算法在锚节点数的影响下其定位误差的对比情况。设置总节点数为100、通信半径为30 m,锚节点数量不断按比例改变。随着锚节点比例逐渐提高,各算法的整体定位误差均在逐渐减小,这是因为在锚节点增多的同时,也使得节点跳距估计更加准确、最小跳数更加贴近WSN的真实程度。由表2可知,ISSA-GRNN算法的平均定位误差相比于其他三种算法分别减少了68.8%、64.1%和27.7%,稳定程度也更好。

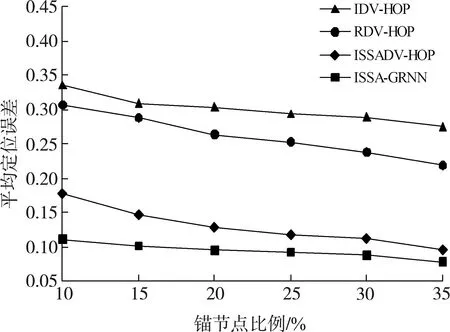
图4 锚节点数对节点定位的影响

表2 锚节点数影响下的平均定位误差对比

3.3 总节点数对节点定位的影响

图5为不同定位算法在总节点数的影响下其定位误差的对比情况。设置锚节点比例为0.3、通信半径为30 m,总节点数不断改变。当总节点数逐渐增多时,WSN区域连通性也在不断增强,因此保存了更多的节点定位信息,使得定位误差不断减少。由表3可知,ISSA-GRNN算法的平均定位误差相比其他三种算法分别减少了73.0%、64.8%和21.4%。

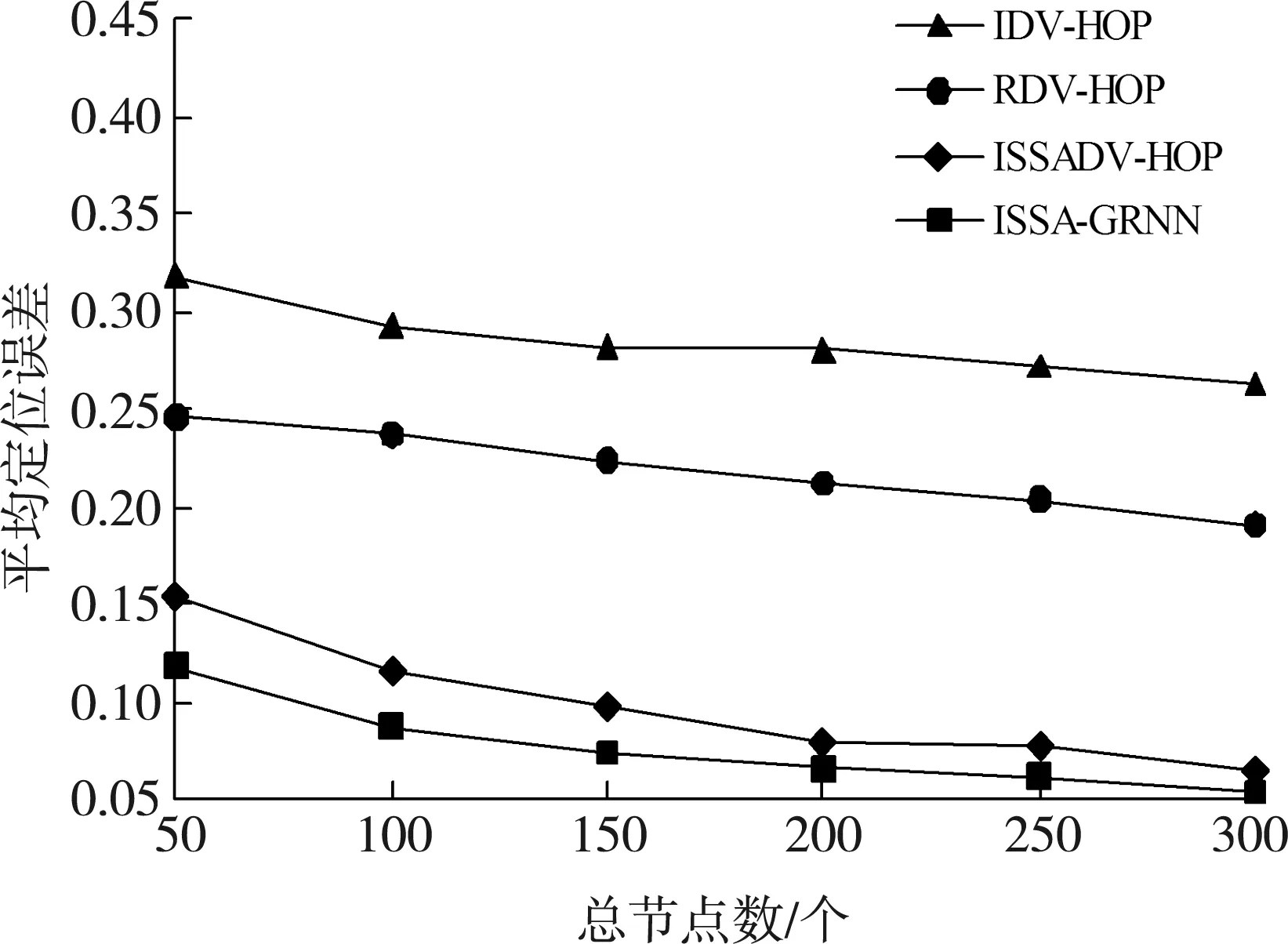
图5 总节点数对节点定位的影响

表3 总节点数影响下的平均定位误差对比

总之,本文提出的ISSA-GRNN算法定位效果更稳定、定位精度更高。

4 结 论

本文主要提出了一种ISSA和GRNN结合的优化算法定位WSN未知节点的位置。首先利用LHS初始化SSA种群,然后优化GRNN的网络参数,将加权修正后的节点跳距和质心等重要特征相互融合作为GRNN的输入向量训练网络,并使用交叉验证法处理网络向量值。与其他算法对比的仿真实验结果表明,该优化算法有着较好的定位效果,其定位误差明显小于其他定位算法,增加了节点定位的准确程度。在今后的研究中,可以考虑将此类优化算法应用于三维空间或动态网络中实现WSN节点定位,不断拓展其综合应用范围。