钢渣泡沫混凝土的制备及抗压强度计算方法
2023-01-03李霖霖王宇李辉
李霖霖,王宇,李辉
(1.济南市工程质量与安全中心,山东 济南 250000;2.济南东铁轨道交通建材有限公司,山东 济南 250000)
0 引言
泡沫混凝土是一种通过发泡剂将空气截留在浆体中的轻质混凝土[1],具有流动性高、水泥用量低、集料消耗少、质量轻和隔热性能好等优点[2]。钢渣是炼钢工业产生的一种副产品,我国钢渣以每年1亿t产生量位居世界第一[3]。近年来钢渣利用率相对较低,大部分作为填埋处理[4]。据测算,如果用钢渣作为骨料完全替代天然骨料,按制备1 m3的钢渣混凝土,将消耗2000 kg以上的钢渣,可节省1500 kg以上的天然骨料。另外,有研究者发现[5],钢渣作为集料使用时,混凝土的强度、耐磨、抗冻及耐腐蚀等方面的性能优于天然骨料。近年来,有关钢渣透水混凝土制备和性能的研究已取得一定的进展。黄凯健等[6]采用钢渣取代碎石制备钢渣混凝土,并分析了掺合料和聚合物配比对透水混凝土的影响。黄嘉祺等[7]研究发现,钢渣中活性CaO与CO2反应形成CaCO3,可以利用碳激发技术制备钢渣生态多孔混凝土。周学军等[8]探讨了多种因素对钢渣泡沫混凝土(SSFC)强度和导热系数的影响,得出钢渣掺量和水胶比对抗压强度和导热系数均有较大影响,且得出了水胶比和钢渣掺量的最优配合比。
鉴于SSFC在土木工程中具有广阔的应用前景,有必要了解其抗压强度的计算方法,为其在工程中的应用提供参考。目前已有较多学者对泡沫混凝土的抗压强度进行了研究[9-10],发现抗压强度与孔隙率(或气泡率)密切相关。通常抗压强度随着孔隙率的增加而降低,孔隙率也常被用来预测SSFC的抗压强度[11]。项国圣等[12]研究发现,SSFC的抗压强度与其气泡率之间存在指数函数关系。基于Balshin给出的多孔材料的抗压强度与孔隙率之间的关系式,Nguyen等[13]提出了SSFC强度与孔隙率的Hoff计算模型。Kearsley和Wainwright[14]指出,Hoff模型可以有效地预测不同龄期、不同孔隙率的SSFC抗压强度,但Hoff模型中计算参数多为经验值或试验数据拟合值,不便于应用。
本文将钢渣作为混凝土集料,通过探讨钢渣粒径、取代率及水胶比对SSFC抗压强度的影响,得出试验的最优配合比,然后分别采用SEM图像法以及50、100、150、200 mm 4种立方体SSFC抗压强度计算出SSFC的分形维数,据此建立SSFC抗压强度与其孔隙率之间的分形关系,为预测SSFC的强度提供一种简便方法。
1 钢渣泡沫混凝土的制备
1.1 原材料
水泥:P·O 42.5级;钢渣:梅山钢铁公司的转炉钢渣;复合型水泥发泡剂:HTW-1型,河南华泰新材公司;水:自来水。表1为水泥和钢渣的主要化学成分,可见钢渣的化学成分与水泥成分相似,可部分取代水泥。

表1 水泥和钢渣的化学成分 %
1.2 试样的配合比设计和制备
试验探讨了钢渣粒径、钢渣取代率和水胶比(0.3、0.4、0.5)对SSFC抗压强度的影响。钢渣进行筛分后,选择钢渣最大粒径分别为0.60、1.18、2.36 mm的连续级配;钢渣取代率分别取0、10%、20%、30%、40%、50%。
按照设计配合比称取钢渣和水泥,干拌均匀,然后分批放入水泥发泡一体机并加水搅拌。同时将发泡剂稀释放入发泡装置,待发泡稳定后将气泡加入到水泥浆中,通过控制发泡时间获得不同气泡含量。将水泥浆与气泡搅拌3 min,使气泡分布均匀,然后将浆液倒入试模中,24 h后拆模,标准养护至预定龄期后测试抗压强度。
1.3 最优配合比的确定
钢渣粒径、取代率及水胶比对SSFC抗压强度的影响如图1所示。其中抗压强度取3个试样的平均值,试样目标孔隙率为60%,干密度约700 kg/m3,养护龄期为7 d。
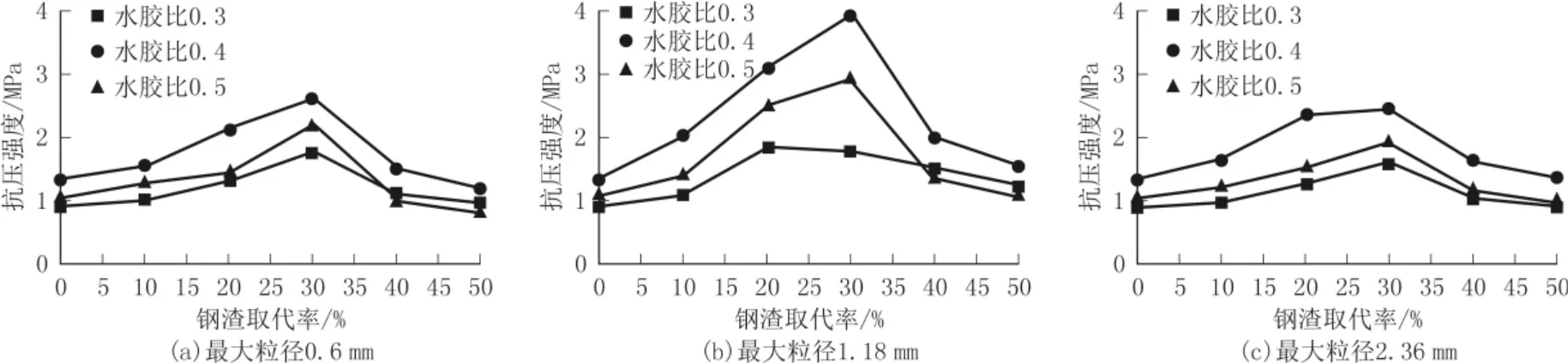
图1 钢渣粒径、取代率及水胶比对SSFC抗压强度的影响
由图1可以看出:
(1)钢渣粒径及水胶比相同时,随着钢渣取代率的增加,各试块的7 d抗压强度先提高后降低,且大部分试块7 d抗压强度在钢渣取代率为30%时达到最高。表明添加了一定量的钢渣能有效增强抗压强度,这一过程由于水泥和钢渣之间具有较好协同效应,因此可以提高相互的水化反应,从而产生了更多水化产物[15]。另外,钢渣取代率在0~550时,SSFC的孔隙结构比较均匀,连通孔隙较少,平均孔径较小,结构更密实[16]。但当钢渣取代率较大时,由于钢渣密度较大,浆体易发生分层离析现象,气泡分布不均匀,试块上下部分干体积密度不一致,结构疏松,易破坏,导致试块强度较低。因此钢渣取代率过小或过大时,试块抗压强度均较低,而掺入适量的钢渣有利于提高试样的抗压强度。
(2)钢渣粒径和取代率相同时,水胶比为0.4的试样抗压强度总是高于水胶比为0.3和0.5的试样。这主要是由于当水胶比较小时,浆体的流动性较低,泡沫与浆体难以搅拌均匀,混合过程中泡沫易发生破裂;且水分较少时,水泥和钢渣的水化反应也不充分,使得胶凝物质相对较少,抗压强度较低。但当水胶比较大时,上层浆体流动性较大,气泡易上移,浆体容易沉降,泡沫与浆体难以混合均匀,且水胶比越大,沉降现象越明显,甚至会发生分层现象,从而导致其抗压强度较低。因此,SSFC制作时也应控制合适的水胶比。
(3)对比3种钢渣粒径下SSFC的7 d抗压强度可以发现,钢渣取代率和水胶比相同时,钢渣最大粒径为1.18 mm连续级配下制备的SSFC具有最高的抗压强度。这主要是由于本次试验中未采用常规天然集料,当钢渣粒径过小时,钢渣不能作为集料给试块提供充足的强度;而当钢渣粒径过大时,大颗粒钢渣之间的孔隙较大,会造成试块内部含有大孔隙,结构不够稳定,导致其抗压强度较低。
由上述试验可以得出,此3种因素下的最优配合比为:钢渣取代率为30%,钢渣最大粒径为1.18 mm,水胶比为0.4,此时SSFC的7 d抗压强度为3.96 MPa。
2 抗压强度的计算
2.1 抗压强度与孔隙率之间的分形关系
根据分形理论,混凝土原生胶体颗粒的数量与其尺寸之间的关系可用式(1)表示[17]:

其中:N——原生胶体颗粒数量;
fc——比例因子;
D——SSFC的分形维数;
dp——胶体颗粒直径;
dc——计量参数。
假设原生颗粒为球形,SSFC中原生颗粒数N=(1-φ)dc3,则SSFC的泡沫率可由式(2)得出[18]:

众多胶体颗粒组成了SSFC的胶结网,因此混凝土的抗压强度取决于颗粒间的吸引键强度和需要断开的键数。其中颗粒间吸引健的强度由颗粒间吸引力决定,需要断裂的吸引键的数量取决于网络结构因素和颗粒参数,如颗粒大小、形状等[18]。因此,SSFC的抗压强度由其有效骨架决定,SSFC的骨架也为分形体。与SSFC的分形维数D不同,SSFC的骨干分形维数X是描述骨干网络结构的指标[18]。SSFC的颗粒间吸引键数目是骨干分形维数的函数,Son和Hsu[19]给出SSFC中心截面上颗粒间吸引键的数目可以用式(3)表示:

式中:X——SSFC的骨干分形维数,根据Mandelbrot的经验法则,骨干分形维数X=D-1。
抗压强度的大小应为所有粘结力之和,即SSFC的破碎力可以认为是SSFC中颗粒键数目与颗粒间吸引力的乘积。而SSFC的抗压强度可以用破碎力除以截面面积来表示,因此SSFC的抗压强度可用式(4)表示:

式中:σf0——泡沫率φ=0时SSFC的抗压强度,MPa;
结合式(1)和式(3),抗压强度可用泡沫率φ表示为式(5):

式中:b=(D-1)/3(3-D)。
2.2 泡沫混凝土分形维数的计算
SSFC的抗压强度可由式(6)计算:

式中:σf——抗压强度,MPa;
Ff——破碎力,kN;
Aapp——垂直于破碎力Ff的截面中SSFC试块的表观面积,m2;表观面积与立方体试件尺寸d的关系为Aapp=d2。
SSFC是一种多孔分形结构,设在三维中分形维数为D,则在二维截面上的分形维数为D-1。垂直于破碎力Ff的截面中SSFC试块的实际面积按式(7)表示为[20]:

式中:Areal——垂直于破碎力Ff的截面中SSFC试块的实际面积,m2。

假设材料一定时,颗粒的密实抗压强度是恒定的,不随SSFC的立方体试件尺寸变化而变化。而由于孔隙的存在,结合式(6)~式(8),可以得出混凝土的抗压强度σf与立方体试件尺寸d存在式(9)关系:

根据式(9),SSFC的分形维数可采用不同尺寸d的混凝土抗压强度计算得出。图2为采用不同尺寸的SSFC试件计算得到的分形维数,7、14、28 d时试件的分形维数均在2.75左右,表明龄期对SSFC的分形维数没有影响。
SSFC的分形维数也可采用SEM图像法测得。SEM所测试件在横断面截取5 mm×5 mm大小的片状材料,扫描前依照要求对测试试件进行真空镀金。本研究选择差分盒维法对SSFC的SEM图像进行分析,并采用MATLAB软件计算SEM图像的计盒维数Ds,对图像进行二值化处理(见图3),将图像转化为0和1的矩阵。降低SEM图像的像素尺寸,则对应的计盒数逐渐增加。当计盒边长ε趋于0时,理论上计盒数N(ε)趋于无穷。再以ln(ε)为横坐标,lnN(ε)为纵坐标进行拟合,lnN(ε)-ln(ε)斜率的负值便是SEM分形图像的计盒维数Ds,用式(10)表示:

式中:ε——计盒边长,μm;
N(ε)——计盒数。
由此计算出SSFC的SEM图像计盒维数Ds为1.74,则三维分形维数为2.74,该值与式(9)计算得到的分形维数基本一致。

图3 SSFC的SEM图像及二值化处理
2.3 分形维数计算方法验证
根据前文测试可知,SSFC的分形维数约为2.75,则参数b的值为2.33。利用参数b和式(5)对SSFC的抗压强度进行预测(见图4),可以发现,养护7、28、60、90 d后SSFC抗压强度与泡沫率φ之间的关系符合式(5),均可表达成式(11):

式中无泡沫时混凝土的抗压强度σf0随着龄期的延长而提高。将不同龄期SSFC的抗压强度与泡沫率的关系列于表2,拟合优度R2均超过0.97,可见预测值与试验值吻合较好。由此可见,多孔结构的分形模型为计算SSFC的抗压强度提供了一种简单有效的方法。
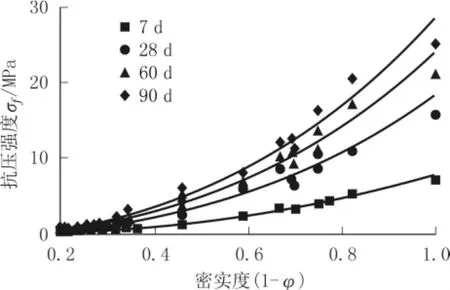
图4 SSFC抗压强度预测值与试验值对比

表2 抗压强度与泡沫率之间的关系
3 结论
(1)通过7 d抗压强度可以确定SSFC的最优配合比为:钢渣最大粒径为1.18 mm、钢渣取代率为30%、水胶比为0.4,此时干密度等级为700 kg/m3的SSFC 7 d抗压强度可达3.96 MPa。
(2)SSFC的抗压强度与泡沫率之间存在分形关系,SSFC的分形维数可由SEM图像以及抗压强度与尺寸之间的关系计算,2种方法计算的分形维数基本相同。结合分形维数以及抗压强度与龄期的幂函数关系,可以计算出龄期和泡沫率不同时SSFC的抗压强度,该模型为SSFC的抗压强度提供了有效的预测方法。
