不同跨度下景区悬索威亚承载钢丝绳的张力计算与安全性分析

赵九峰

(1.河南省特种设备安全检测研究院，郑州 450000；2.航空经济发展河南省协同创新中心，郑州 450046)

近年来，国内各大景区为吸引游客，引进了不少高空、高速、高风险的网红项目，这些项目备受年轻人的追捧.自 20世纪中叶以来，悬索威亚逐渐成为电影拍摄、舞台特技表演中一种常用的设备.2008年北京奥运会开幕式上的“飞天”表演，就灵活应用了威亚[1].威亚是英文wire的译音，wire的中文译义是钢丝.由于建设投资少、易安装、回本快，悬索威亚设备在景区被大量安装.景区悬索威亚并未纳入特种设备目录，没有任何现行的规范可以依循，往往依据以往的经验进行建设，存在许多安全隐患.近年来，景区悬索威亚娱乐项目发生多起事故，严重威胁乘客的生命安全[2].

景区悬索威亚主要依靠承载钢丝绳上小车的运行来实现乘客的移动.承载钢丝绳是悬索威亚设备的关键部件，其张力的正确计算是当前景区悬索威亚设计的主要难点[3].本文在承载钢丝绳受力原理解析的基础上，详细推导钢丝绳张力的计算公式，并结合实例，分别应用力学理论和有限元仿真技术，同时借助游乐设施滑索方面的技术标准，计算钢丝绳张力的安全系数，进而确定现有景区悬索威亚的合理跨度.该研究方法为景区悬索威亚的设计、安装提供了指导，对保障设备的安全运行和乘客的生命安全具有重要意义.

1 景区悬索威亚的组成及工作原理

目前常见的悬索威亚有一维、二维和三维3种情况.一维悬索威亚类似单点吊机，仅进行上下升降运动；二维悬索威亚能在某一给定平面内进行上下升降、水平运动以及平面内的复合运动；三维悬索威亚能在一定范围的三维空间内进行任意运动[4].目前国内景区悬索威亚主要为二维悬索威亚，其结构简图如图1所示.

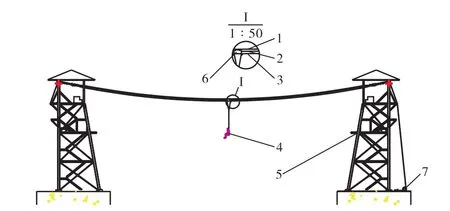
图1 景区悬索威亚的示意图Fig.1 Schematic diagram of wire suspension in the scenic spot

景区悬索威亚通常由两根承载钢丝绳、一根牵引钢丝绳、两根升降钢丝绳、两组立柱支架、一辆悬索威亚小车和一套驱动控制系统组成.在两个等高度的立柱支架之间架设两根承载钢丝绳，乘客通过升降钢丝绳与悬索威亚小车相连，靠牵引钢丝绳拖动悬索威亚小车在承载钢丝绳上前后运动.

景区悬索威亚安装的两根承载钢丝绳是悬索威亚小车运行的轨道，承载钢丝绳悬挂在两侧立柱支架的顶部，立柱支架一般跨过河流或湖泊；牵引钢丝绳一端连接小车，另一端通过滑轮连接地面的卷扬机，通过卷扬机的正反转控制悬索威亚小车的前后水平运动；升降钢丝绳与穿在乘客身上的悬索威亚衣相连，通过另一套独立的驱动系统控制乘客的升降.

承载钢丝绳是景区悬索威亚的“生命线”，承载着悬索威亚小车和乘客的重力等[3].为了体现更好的视觉效果，承载钢丝绳一般较细[5]，因此景区悬索威亚安全的关键是对承载钢丝绳的受力情况进行正确的计算，确定合理的跨度.

2 钢丝绳载荷特性分析

2.1 钢丝绳张力数学模型

景区悬索威亚承载钢丝绳的实质是两端固定的悬链曲线[6].在悬索威亚小车和乘客的重力的作用下，承载钢丝绳被分为可近似为两段直线的悬线.悬索威亚小车在承载钢丝绳上任一位置时，承载钢丝绳载荷示意图如图2所示.

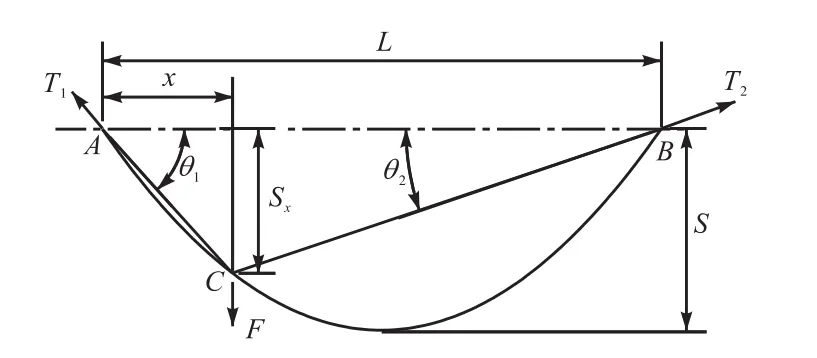
图2 承载钢丝绳载荷示意图Fig.2 Schematic diagram of carrying steel wire rope load

弦多边原理认为，集中载荷点之间的弦(索段)，在重力作用下不会变形，每段弦(索段)受到的重力，平均分配到弦(索段)的两个端点.

承载钢丝绳的悬挂点为同一水平线上的 A、B两点，假设悬索威亚小车运行到钢丝绳上的任意一点C，在悬索威亚小车和乘客产生的载荷的作用下，钢丝绳趋于形成 AC、BC两条线段.根据弦多边原理[3]，C点的集中载荷为

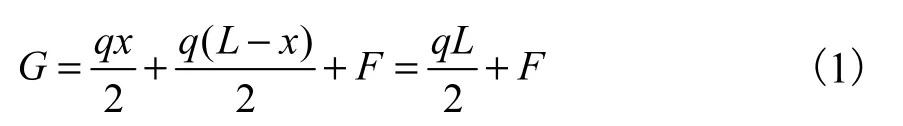
式中：G 为 C点的集中载荷，N；q为钢丝绳单位长度上自重产生的均布载荷，N/m；x为A点与 C点的水平距离，m；L为 A、B两点的距离即悬索威亚承载钢丝绳的跨度，m；F为悬索威亚小车和乘客产生的集中载荷，N.

2.2 水平张力

钢丝绳是柔性构件，仅能承受张力[7]，C点在AC段的张力 T1(单位为 N)和 BC段的张力 T2(单位为N)的合力的作用下处于静止平衡状态，C点水平方向静力平衡，C点受到的单侧水平张力为Tsp(单位为N)，由平衡方程有

即

同理，根据C点竖直方向的平衡方程可得

将式(3)代入式(4)可得

在三角形ABC中，根据三角函数关系可得

将式(6)代入式(5)可得

联立式(1)、式(7)可得

由式(8)可得钢丝绳的水平张力的二次函数

式中：S为承载钢丝绳的中央挠度，m；S=λL，λ为中央挠度系数，一般取λ＝0.03～0.05[8].

取中央挠度系数λ＝0.04，则 S＝0.04L，代入式(10)可得钢丝绳的水平张力

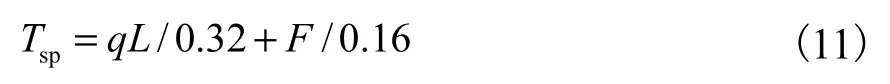
2.3 竖直张力

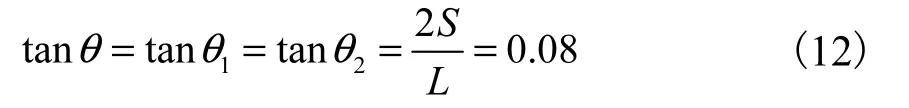
承载钢丝绳悬挂点A、B两点，在竖直方向上受到 3种载荷：钢丝绳的自重载荷qL、小车和乘客的集中载荷F、钢丝绳端张力的竖直分量.根据力的平衡可得悬挂点处钢丝绳的竖直张力

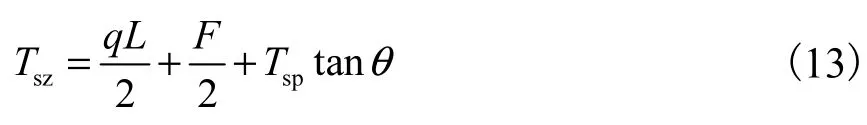
联立式(11)—式(13)可得

2.4 钢丝绳张力与校核

由2.2节和2.3节分别得出景区悬索威亚钢丝绳的水平张力和竖直张力，则景区悬索威亚钢丝绳的总张力T为

参考 GB/T 31258—2014《滑索通用技术条件》3.5节中的要求，承载索的安全系数(钢丝绳最小破断张力与最大计算张力之比)应不小于 5[9]，可得到钢丝绳的安全系数n.

式中：Tp为钢丝绳的破断张力，N；[n]为许用安全系数，取值为5.0.

3 实例计算

一般景区悬索威亚的长度控制在 100～300m，为了呈现更好的视觉效果，常选用直径6mm的线接触、交互捻钢芯镀锌钢丝绳，由《机械设计手册》可知直径 6mm 钢丝绳的破断张力 Tp＝22.6kN，单位长度的均布载荷 q＝1.46N/m[10].悬索威亚小车和乘客的载荷为850N，运行中考虑1.2倍的冲击系数[11]，则总载荷为 850×1.2＝1020N，景区悬索威亚为双索结构，单根承载钢丝绳上集中载荷F＝510N.

将已知数据代入式(11)、式(14)、式(15)，可得方程组

承载钢丝绳的跨度 L通常为 200～300m，分别取 L 为 200、220、240、260、280、300m，代入到方程组(17)中，可求得不同跨度下的景区悬索威亚承载钢丝绳张力理论计算结果，结果见表1.

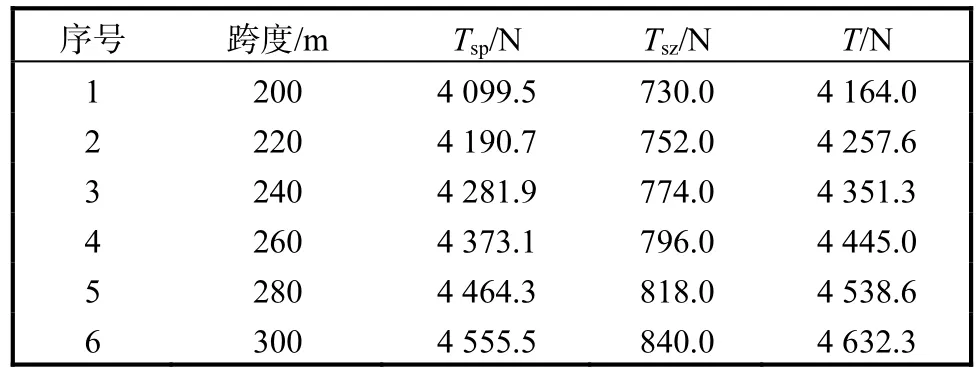
表1 悬索威亚承载钢丝绳张力理论计算结果Tab.1 Theoretical calculation results of the tension of bearing steel wire rope of the wire suspension

4 有限元分析

大跨度悬链钢丝绳形态确定和受力分析是一个典型的几何非线性大位移问题，几何外形的微小变化都会引起结构性能的较大变化[12].利用 ANSYS Workbench软件的静力学分析模块Static Structure的曲线拟合功能，对景区悬索威亚承载钢丝绳进行三维建模，钢丝绳中央挠度为跨度的0.04倍，采用索单元Link180，单元两节点不传递扭矩，只有三向平移自由度[13].承载钢丝绳的直径为 6mm，弹性模量为120GPa，钢丝绳的密度为5270kg/m3.

承载钢丝绳两端施加位移约束(displacement)，中部施加向下的集中载荷F为510N，整体施加向下的重力加速度为 9.8m/s2，选取无风工况进行有限元分析计算，载荷与约束如图3所示.

图3 承载钢丝绳载荷与约束Fig.3 Load and restraint of bearing steel wire rope

由于大跨度钢丝绳的应变-位移为非线性关系，所以在求解时设置大变形(large deflection)选项为打开状态(on)[14]，进行大变形静力分析.

以跨度为 200m的悬索威亚承载钢丝绳为研究对象，对有限元结果进行评价.合理的有限元结果是网格无关解，在网格精细化到一定程度后，结果不再随着网格的变化而变化.设置单元尺寸分别为20m、10m、5m、2m，单元尺寸对钢丝绳张力的影响结果如图4所示.由图4可知：在单元网格逐渐变密的过程中，钢丝绳张力改变率逐渐变小；单元尺寸由 5m减小到2m后，钢丝绳张力的改变率约0.1%，计算结果是收敛的，可以认为张力解是网格无关解.

图4 单元尺寸对钢丝绳张力的影响Fig.4 Effect of unit size on wire rope tension

跨度为200m时，承载钢丝绳张力分析结果如图5所示.

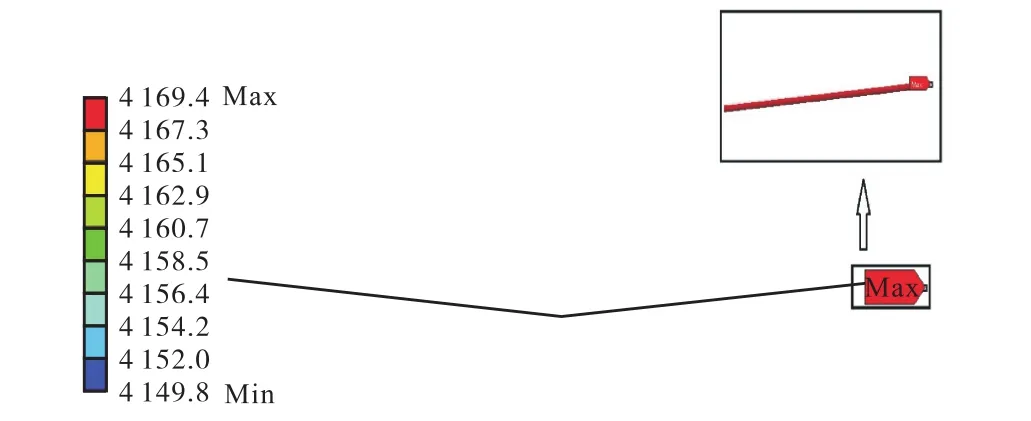
图5 承载钢丝绳张力分析结果(L＝200m)Fig.5 Tension analysis results of bearing steel wire rope(L＝200m)

同理，在有限元仿真软件中计算其他跨度下钢丝绳的张力.

通过理论计算获得解析解，通过有限元仿真计算获得仿真解，不同跨度下景区悬索威亚钢丝绳张力解析解与仿真解的结果对比见表2.

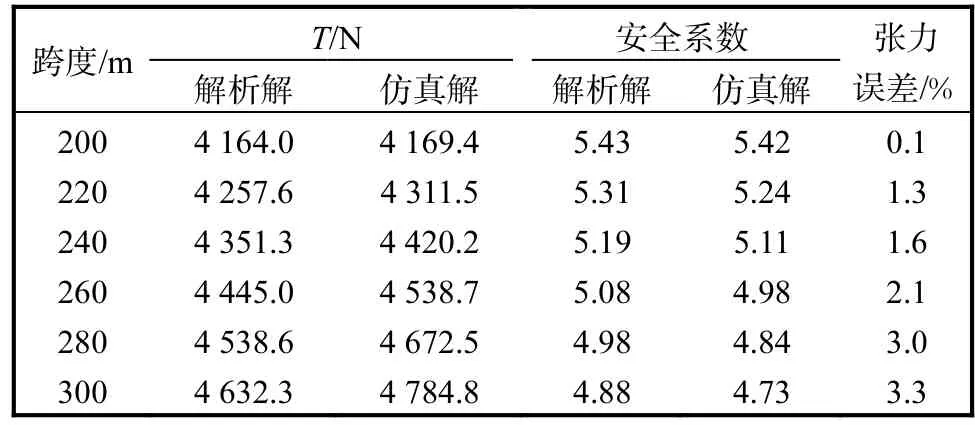
表2 承载钢丝绳张力结果对比Tab.2 Comparison of tension results of bearing steel wire rope

由表2可知：随着景区悬索威亚跨度的增加，承载钢丝绳的张力不断增大.跨度为 300m 时，解析解与仿真解的最大误差为 3.3%，仿真结果基本与理论计算相符，表明了仿真结果的可靠性.

为了计算方便，理论分析过程中取中央挠度系数为恒定值0.04，忽略中央挠度系数随着跨度的增加而偏大的影响因素，使得在跨度增加时悬索威亚承载钢丝绳张力的解析解偏小，导致在表2中解析解和仿真解的误差随跨度增加而增大.

5 安全性分析

通过式(16)分别计算6种跨度下，景区悬索威亚承载钢丝绳张力解析解和仿真解的安全系数，结果见表2.由表2可知：承载钢丝绳张力的安全系数随着跨度的增大而减小，景区悬索威亚最大跨度为 240m时，承载钢丝绳张力解析解和仿真解的安全系数分别为 5.19和 5.11，均大于 5.0，表明钢丝绳符合安全要求[15].因此，对景区悬索威亚常用的直径 6mm 承载钢丝绳而言，跨度应限制在240m以内.

计算中未考虑风载荷和钢丝绳端部固定效率的影响.综上所述，针对直径 6mm 的承载钢丝绳，为了确保乘客的安全，推荐景区悬索威亚的最大跨度为200m.

6 结 论

利用弦多边理论对景区悬索威亚钢丝绳的张力计算公式进行详细推导，结合实例对6种跨度下的解析解和仿真解进行对比和分析，实现了理论推导和仿真实验的相互印证，结果表明：

(1)景区悬索威亚承载钢丝绳张力的安全系数随着跨度的增大而减小，钢丝绳张力解析解与仿真解的最大误差为 3.3%，表明了数值仿真计算结果的可靠性.

(2)景区悬索威亚最大跨度为 240m 时，承载钢丝绳张力仿真解的安全系数为 5.11，大于 5.0，表明钢丝绳符合安全要求，对景区悬索威亚常用的直径6mm的承载钢丝绳，推荐最大跨度为240m.

(3)计算中未考虑风载荷的影响，以及钢丝绳端部与立柱支架的固定效率，若考虑以上因素，承载钢丝绳的安全系数会进一步降低.因此，针对直径6mm的承载钢丝绳，推荐景区悬索威亚的最大跨度为200m.