仿人机器人PID控制优化仿真研究
2023-01-03杨坤漓许洋洋
杨坤漓,许洋洋
(郑州工业应用技术学院机电工程学院,河南 郑州 451150)
仿人机器人涉及多种学科和技术,可以服务于社会的各行各业,是近年来研究的热点问题之一。仿人机器人与人体结构非常相似,可以替代人类执行许多复杂任务[1-2],但必须具备先进的控制理论和处理数据的能力,保证仿人机器人运动的稳定性。与双轮或者履带式机器人相比,仿人机器人可在不平整崎岖路面行走,使其在应用领域迅速发展。仿人机器人步行控制问题仍然是较难解决的问题之一,在步行状态下运动控制系统属于非线性和强耦合,控制起来较为复杂。因此,控制系统的设计不仅要保证机器人步行稳定,还要保证机器人能够按照期望轨迹行走,同时应考虑路面障碍物的干扰对控制系统的影响。仿人机器人控制系统研究,需要科研人员继续深入研究。
为了提高仿人机器人的响应速度和运动精度,科研人员对仿人机器人做了大量的工作。文献[3-4]研究了仿人机器人越障步态规划方法,建立了机器人下肢坐标图,利用D-H坐标法得到机器人位姿坐标方程式,通过逆运动学求解机器人各个关节角度,采用Matlab 软件对仿人机器人越障进行仿真,能够按照路径规划进行运动。文献[5]研究了仿人机器人二阶锥控制方法,创建了七连杆仿人机器人模型,设计了二阶锥控制方式,对控制方式添加约束条件,搭建仿真实验平台进行误差仿真验证,采用二阶锥控制方式,能够提高仿人机器人运动的稳定性,降低其输出误差。文献[6]研究了仿人机器人预观控制方法,建立了仿人机器人倒立摆数学模型,推导机器人运动状态方程式,定义机器人误差目标函数,提出了倒立摆预观控制方法,利用Matlab软件对机器人运动轨迹进行仿真,提高了仿人机器人运动的稳定性。文献[7]研究了仿人机器人PID 控制方法,创建了机器人关节数学模型,推导出仿人机器人位姿方程式,设计了仿人机器人关节PID 控制器,提高了轨迹跟踪精度。以往研究的控制系统大多响应速度慢,在避障过程中,导致机器人运动路径长,能源消耗严重。对此,本文建立了仿人机器人线性倒立摆模型,推导出运动方程式,引用传统PID 控制系统,为了提高控制系统的避障效果,利用粒子群算法(particle swarm optimization,PSO)优化PID 控制系统,从而缩短其避障运动路径,通过Matlab 软件对仿人机器人响应速度和运动路径进行仿真测试,对比优化前和优化后的输出效果,为后期深入研究仿人机器人避障控制系统提供参考。
1 仿人机器人模型
1.1 线性倒立摆模型
仿人机器人由多个自由度和一个自由浮动底座组成,使仿人机器人难以稳定。为了解决这个问题,采用线性倒立摆模型,如图1所示。

图1 线性倒立摆模型Fig.1 Linear inverted pendulum model
仿人机器人运动学方程式[8]表示为

式中:mp为倒立摆锤质量;fr为反作用力;θl为倒立摆锤与垂直方向夹角;g为重力加速度。
为了避免仿人机器人发生翻倒,零力矩点稳定性条件意味着机器人必须保持在支撑多边形中。为了测量零力矩点的位置,假设机器人为1 个单点质量,主要集中在个人的质心上,并且单点质量的运动限制在水平方向上。从图1中可以获得θl的值,并表示为
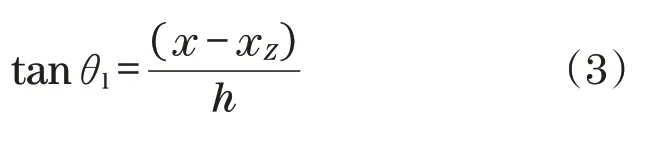
式中:h为摆锤高度;x为机器人质心横向位置;xZ为机器人零力矩点横向位置。
根据线性倒立摆模型,零力矩点和质心条件之间的关系表示为
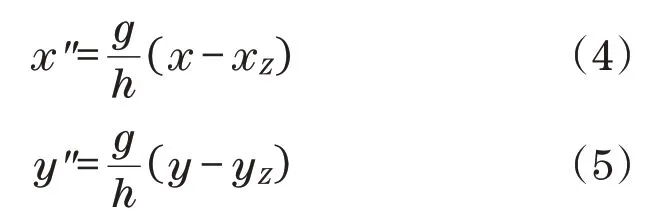
式中:(x,y)为质点坐标的位置;(x-xZ,y-yZ)为零力矩点相对于质心的相对位置坐标。
同理,角加速度可获得如下:

根据初始位移x0和速度x′0可以计算质心运动轨迹,求解如下一阶线性方程:
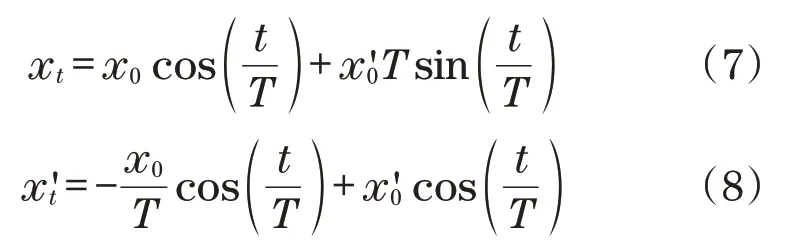
式中:T=;t为时间。
2 控制器优化设计
2.1 PID控制器
PID 控制器是一种具有反馈机制的控制回路系统,广泛应用于工业系统的控制。它嵌入在各种机器人中,用于在不同的环境中控制运动。仿人机器人由闭环PID 控制器控制,PID 控制器的公式[9-10]:
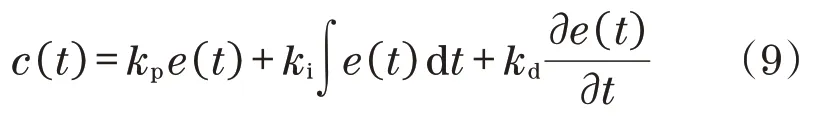
式中:kp为比例增益;ki为积分项;kd为微分项;e(t)为定义误差。
比例增益用于表示与误差信号e(t)等效的控制动作。积分项提供误差信号e(t)的连续积分以最小化稳态误差,而导数项用于改善瞬态响应。误差信号e(t)定义为目标输出和系统输出的差值:
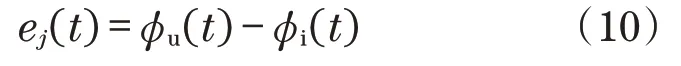
式中:φu(t)为最终角位置;φi(t)为初始角位置。
在执行误差信号后的最终控制动作如下:
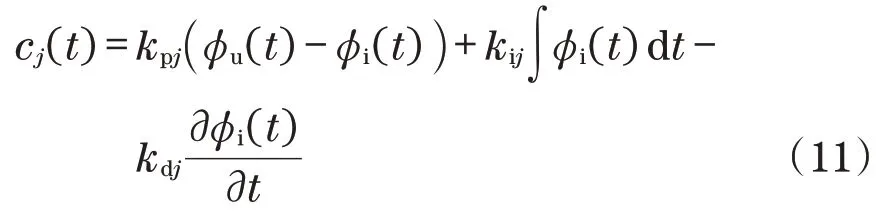
仿人机器人采用传统PID控制框如图2所示。
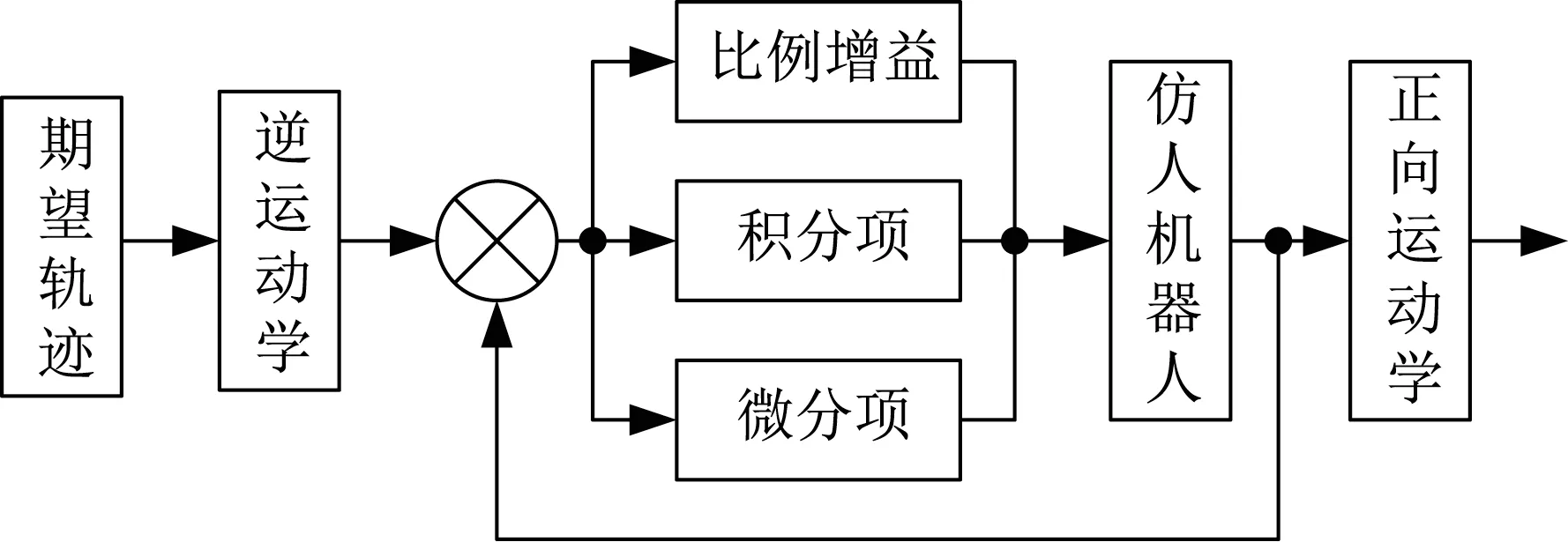
图2 机器人传统PID控制框Fig.2 Traditional PID control block diagram of robot
2.2 PSO优化控制
PSO 是一种进化计算和优化技术,它在通过变异、多重优化、不可微性和非线性寻找高维问题的解决方案方面占主导地位。在PSO优化技术中,粒子群被插入到d维空间中随机选择的速度和位置中,每个粒子的速度根据其自身的飞行经验和另一个粒子的经验进行修改。在d维空间中,粒子的位置pj和速度vj为
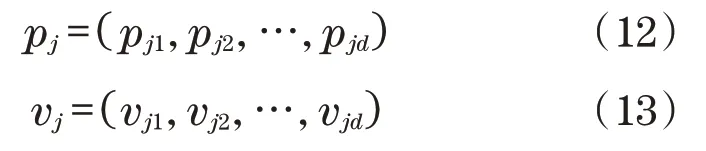
第j个粒子的最优位置如下:
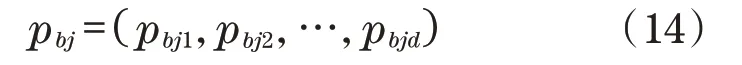
组中所有粒子中的最佳粒子列表为gbjd。在获得群的gbjd(全局最佳位置)和pbjd(每个粒子的最佳位置)的值后,每个粒子的速度和位置[11-12]被修改为
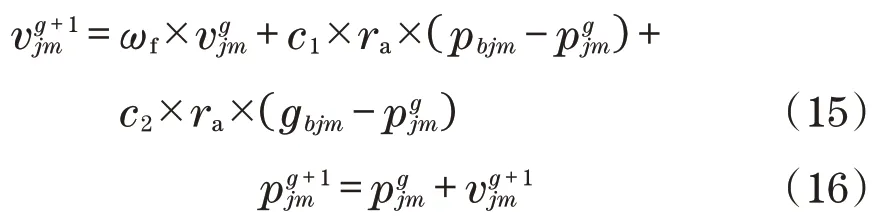
式中:j=1,2,…,n;m=1,2,…,d;ra为[0,1]之间的随机数;c1、c2为学习因子;ωf为惯性权重。
用于仿人机器人运动的PSO 优化技术的流程如图3所示。设计机器人关节角度运动轨迹,利用逆运动学设计机器人关节角度运动轨迹,使得机器人向目标移动。当机器人没有接近障碍物时,如果满足中止条件,则结束,否则机器人继续向目标移动。当机器人靠近障碍物时,机器人获取接近障碍物的初始位置和速度。评价每个粒子的适应度函数,获得每个粒子的最佳函数(局部和全局)。仿人机器人选择最佳角度并向目标移动,如果满足中止条件,则结束,否则返回评价每个粒子的适应度函数。
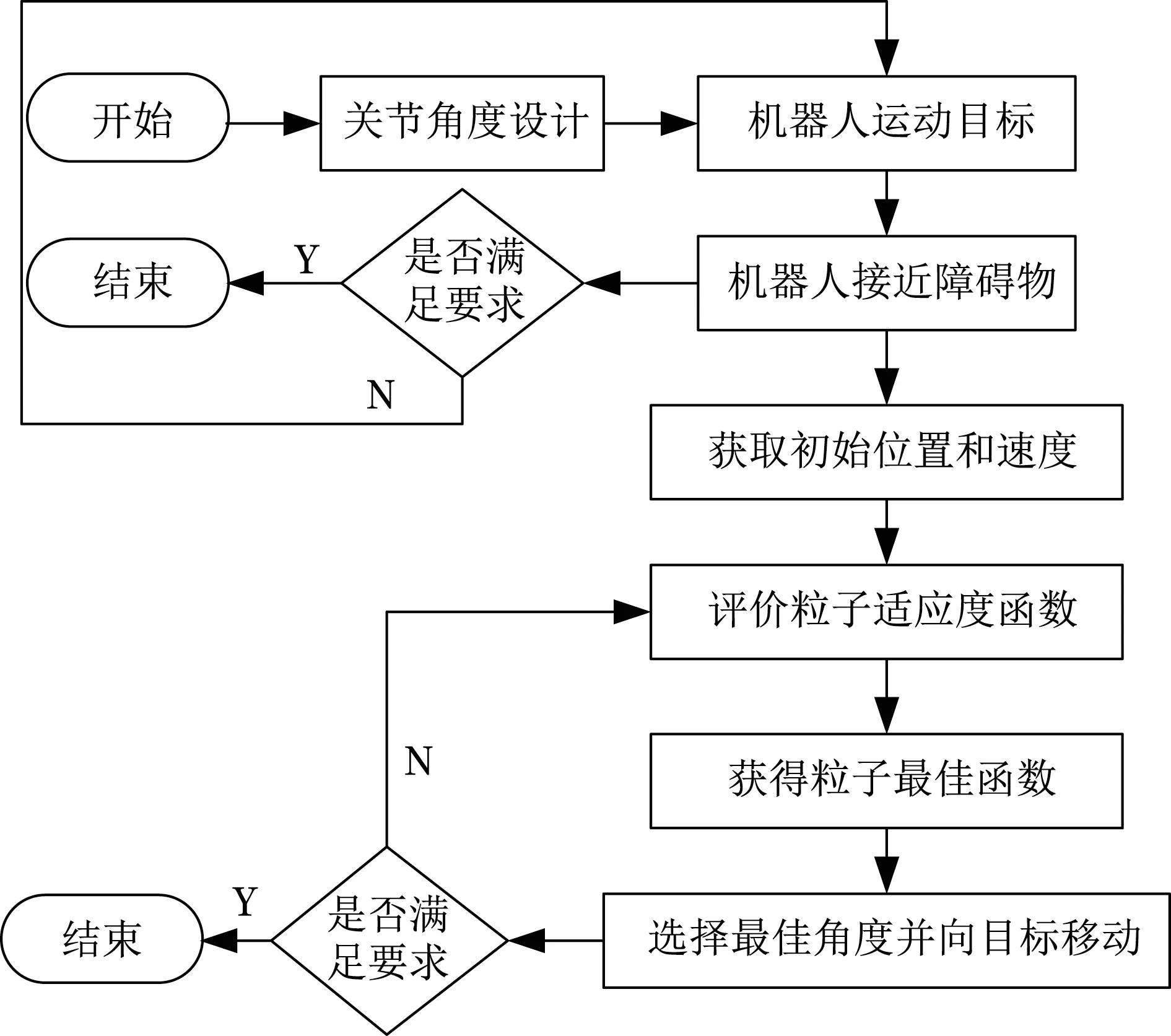
图3 机器人运动优化流程Fig.3 Flow chart of robot motion optimization
为了更好地搜索控制参数全局最优值,学习因子修改为
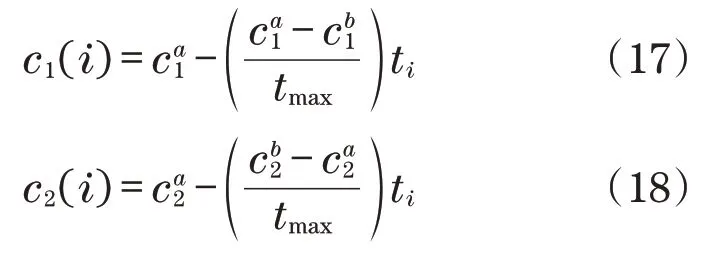
式中:ca1、ca2为学习因子的初始值;cb1、cb2为学习因子的最终值;c1(i)、c2(i)为第i次迭代的学习因子;tmax为最大迭代次数;ti为第i次迭代次数。
为了提高粒子群在局部和全局搜索过程中的搜索能力,引入了惯性权重ωf。ωf值在不同的搜索空间中有所不同。在给定的研究中,ωf的变化显示随时间稳定增加。权重因子的变化∇ωf对参数ωf有影响,该参数在初始搜索中最初时较大,后期开始缩小。惯性权重修改后的方程式如下:
式中:ωf(i)为第i次迭代时的惯性权重;∇ωf=ωmfax-ωmfin。
3 仿真及分析
仿人机器人PID 控制方法通过PSO 优化后,机器人控制系统的响应速度是否提高,机器人跟踪路径是否缩短,需要通过仿真进行进一步验证。利用Matlab 软件对仿人机器人优化后的控制系统进行仿真,仿真参数见表1所示。
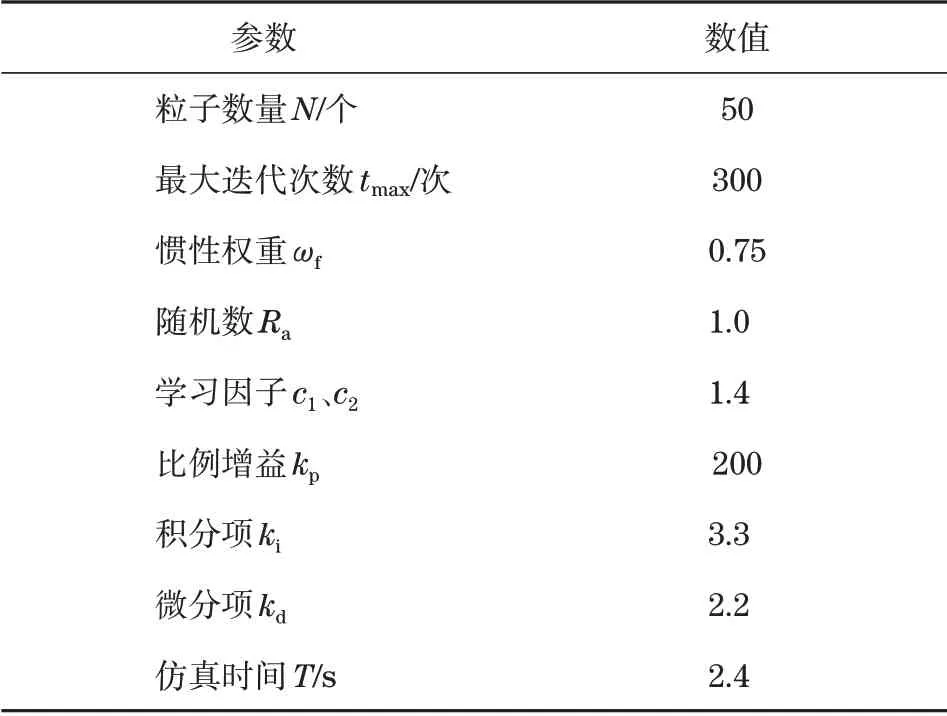
表1 仿真参数Tab.1 Simulation parameters
仿人机器人响应速度采用阶跃波进行仿真测试,其结果如图4所示。仿人机器人路径跟踪采用椭圆形进行测试,在无障碍物环境中,其结果如图5所示;在有障碍物环境中,其结果如图6所示。
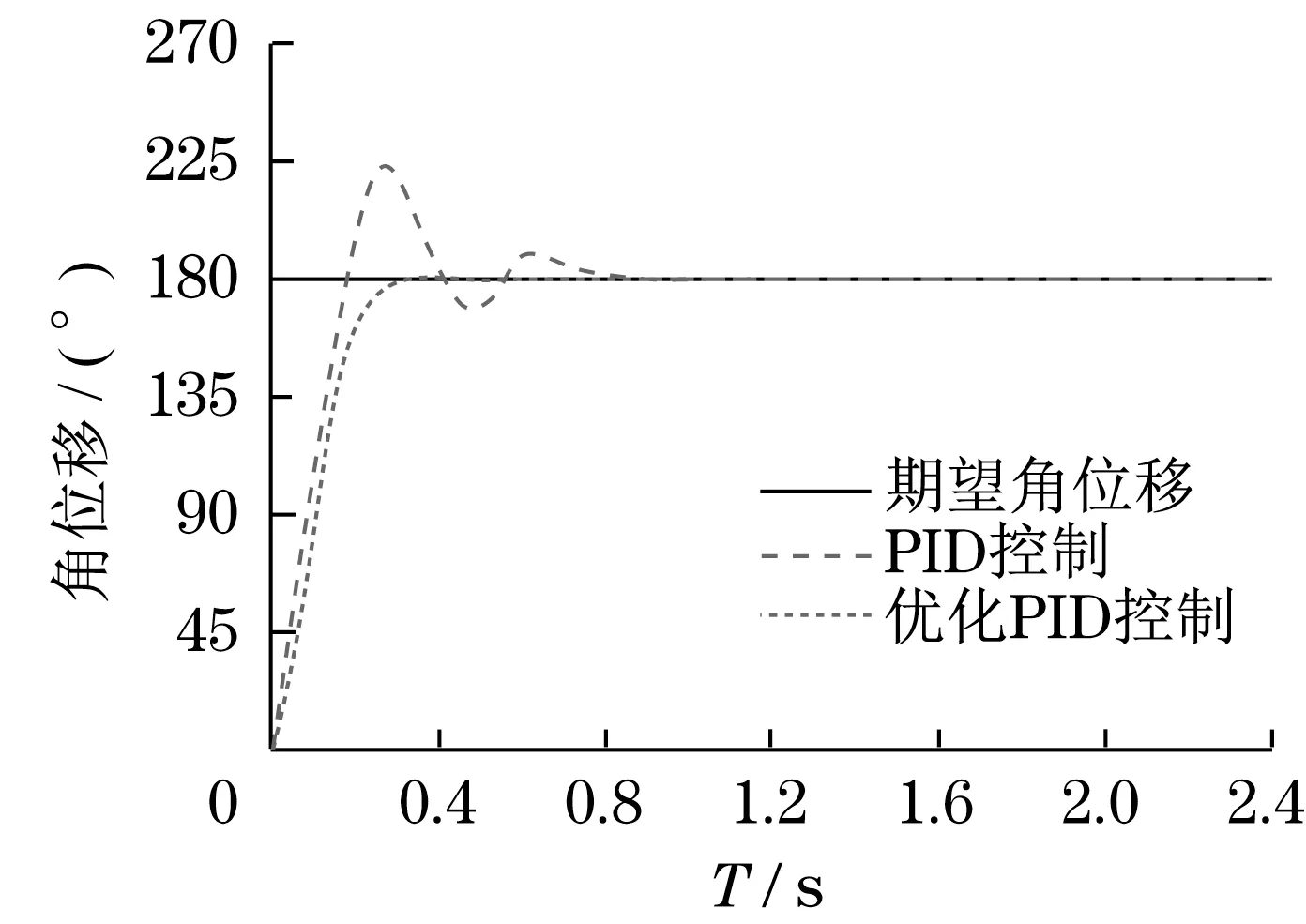
图4 机器人角位移跟踪Fig.4 Robot angular displacement tracking
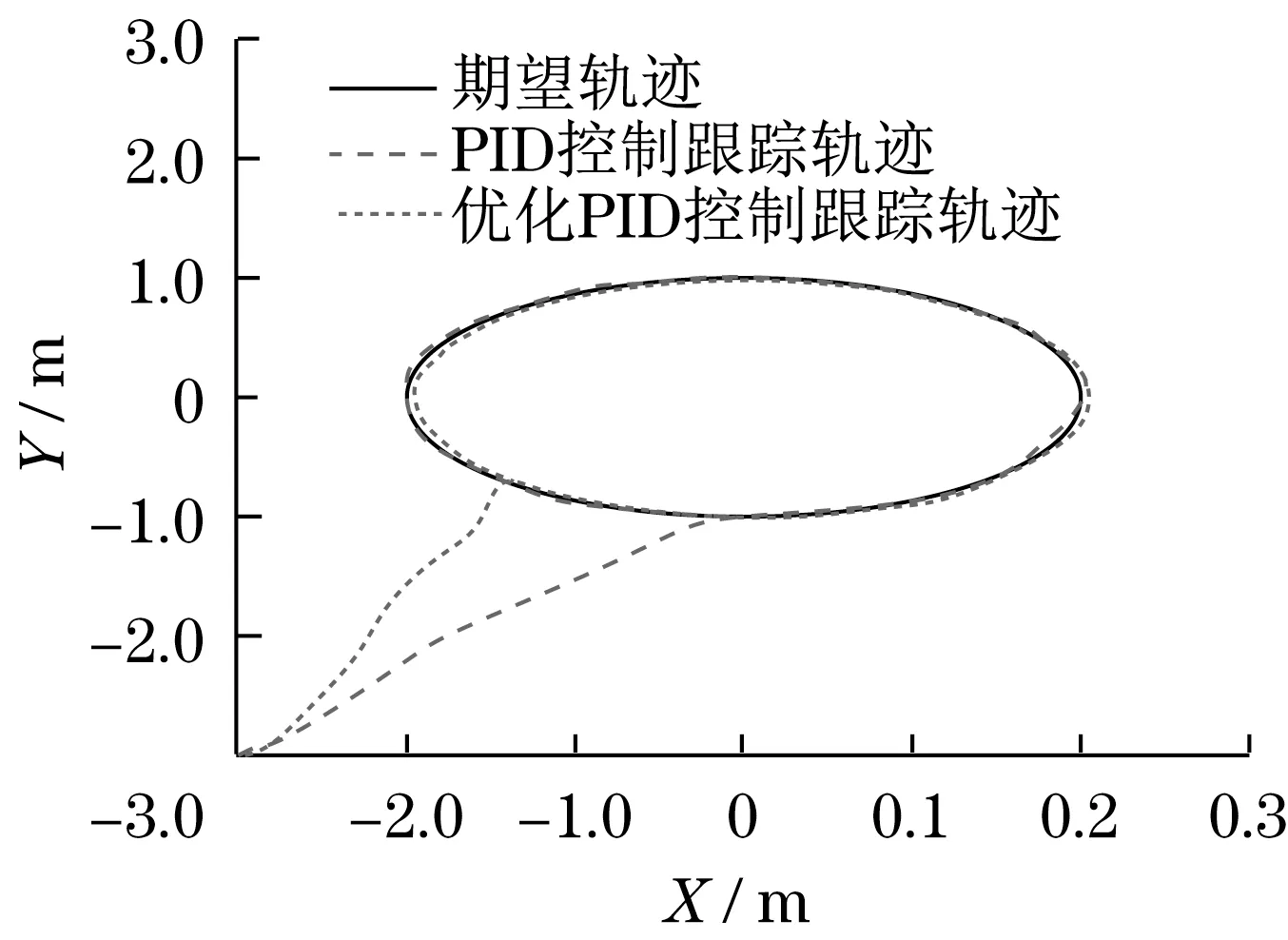
图5 机器人位移跟踪(无障碍物)Fig.5 Robot displacement tracking(no obstacle)
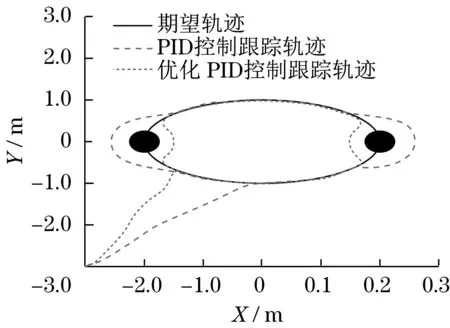
图6 机器人位移跟踪(有障碍物)Fig.6 Robot displacement tracking(with obstacle)
由图4可知:优化前的PID 控制系统,仿人机器人达到稳定状态的时间为0.8 s,超调量为25%;优化后的PID 控制系统,仿人机器人达到稳定状态的时间为0.3 s,超调量为0。由图5可知,在无障碍物环境中,优化前的PID 控制系统,仿人机器人移动到期望运动轨迹所需的路径较长,在跟踪过程中产生的位移误差较小;优化后的PID 控制系统,仿人机器人移动到期望运动轨迹所需的路径较短,在跟踪过程中产生的位移误差较小。由图6可知:在有障碍物环境中,优化前的PID 控制系统,在避障过程中,仿人机器人运动路径较长;优化后的PID 控制系统,在避障过程中,仿人机器人运动路径较短。因此,在同等条件下,仿人机器人采用PSO 优化PID 控制系统,控制系统反应速度较快,超调量较小,在避障过程中,能够快速地搜索到最短路径。
4 结论
针对仿人机器人控制系统反应速度慢、运动路径长等问题,设计优化PID 控制系统,通过仿真验证控制系统输出结果,主要结论如下:
(1)仿人机器人采用传统PID 控制系统,其响应速度较慢,超调量较大,且在避障过程中,运动路径较长;而采用PSO 优化PID 控制系统后,其响应速度较快,超调量较小,运动路径较短,节约了机器人运动能耗。
(2)利用Matlab 软件对仿人机器人响应速度和避障路径进行仿真,能够从理论上检测其避障效果,对后期的改进提供参考,使避障控制系统的设计更加合理。
