带有横向约束的全局优化波阻抗反演方法及应用

朱剑兵，高照奇，田亚军，梁兴城

(1.中国石油化工股份有限公司 胜利油田分公司物探研究院，山东 东营 257022；2.西安交通大学 信息与通信工程学院，陕西 西安 710049)

0 引言

地震反演在油气藏勘探领域中具有重要作用，该方法能够基于地震以及其他地球物理数据估计地下介质参数[1-3]。地震反演往往是通过最小化描述观测地震数据与合成地震数据误差的目标函数来实现的。地震波阻抗反演是一类地震反演问题，其特点是：①模型的非唯一性；②模型和数据的非线性关系，目标函数存在多个局部极小值。

地震波阻抗反演问题的常用求解方法是局部优化算法。这类方法从某一预设的初始模型出发，利用目标函数的梯度信息更新模型参数，如共轭梯度法[4]，最速下降法[5]等。局部优化方法的不足是优化过程中可能陷入目标函数的局部极小值。与局部优化算法不同，全局优化算法不依赖于目标函数的梯度信息，具有跳出目标函数局部极值的能力，因此此类方法越来越多地被应用于求解非线性地震反演问题。在地球物理学中，应用最广泛的全局优化类算法有模拟退火算法及其变体[6-7]，粒子群优化算法[8-9]，遗传算法[10-12]，差分进化算法(differential evolution,DE)[13-15]等。

近年来，DE已经成功地应用于求解地震反问题[16]。但是，维数灾难问题阻碍了DE在高维模型空间反问题中的应用。为了解决这个问题，Potter等[17]提出了协同进化的策略将高维问题分解为多个低维问题进行求解。随后，Wang等[18]提出了协同变异差分进化算法(cooperative coevolutionary DE,CCDE)，其将一个高维模型分解为多个低维子成分，并用“局部适应度函数”来评价每个子成分的质量，用来指导后续变异方向。尽管CCDE在求解高维反问题上比传统DE具有明显的优势，但其对搜索空间的范围敏感。Gao等[19]提出了结合DE/rand/1变异策略和CCDE变异策略的多组变异差分进化算法(multi-mutation DE,MMDE)。该方法对搜索空间的范围不敏感，具有更快的收敛速度。

尽管上述全局优化方法在地震波阻抗反演问题上表现出了优越的性能，但这类方法均采用了逐道反演策略，未考虑模型的空间相关性，导致反演结果的横向连续性差。考虑到地下介质参数是连续变化的，两条相邻地震道之间存在一定的联系。因此，在反演过程中，应考虑当前地震道和相邻地震道之间的相似性。为了解决这一问题，研究者们提出了一些多道反演策略来保证地下结构的横向连续性。Gholami[20]提出了带有TV正则化的多道地震波阻抗反演方法，Zhang等[21]提出了一种基于各向异性全变差(ATV)正则化的多道反演方法。尽管这些假设先验信息的正则化方法可以提高反演模型的横向连续性，但当先验信息与实际情况不符时，这种方法可能会失效。最近，Cheng等[22]提出了一种受两种范数约束的多道反演方法。此外，还针对横向连续性问题引入了卡尔曼滤波器。然而，上述解决横向连续性问题的方法与全局优化算法结合存在难度。

本文提出了一种带有横向约束的多组变异差分进化地震波阻抗反演方法。通过将旁道最优解信息融入到当前地震道的搜索空间中，有效地约束了当前道波阻抗反演的搜索空间范围，实现了逐道反演搜索空间的精确初始化。通过将本文所提出方法与传统多组变异差分进化算法进行对比，实验结果表明，本文所提出方法不仅收敛速度更快，而且反演得到的波阻抗剖面横向连续性更优。此外，本文所提出方法被应用于胜利油田某区块波阻抗反演中，反演结果和测井资料具有很好的一致性，有效地刻画了储层砂岩厚度。

1 带有横向约束的多组变异差分进化算法

1.1 多组变异差分进化算法

多组变异差分进化算法(MMDE)是一种全局优化算法，其算法流程如图 1所示。MMDE主要包含初始化、变异、交叉和选择4个部分，下面将详细介绍这几部分内容。

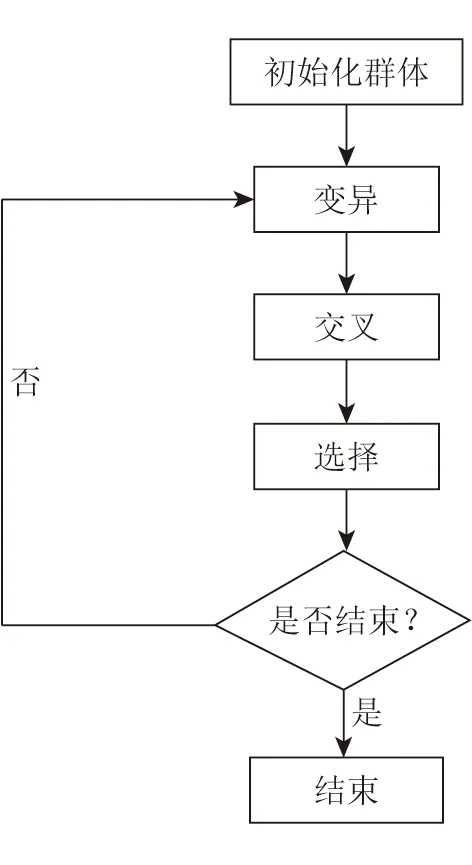
图1 MMDE算法流程

1.1.1 初始化

假设MMDE拟求取一个目标函数f(x)的全局极小值，其中x是一个D维的参数向量x={x1,x2,…,xD}。MMDE首先随机初始化一个种群，种群中有N个个体(候选解)，每一个初始种群中的个体可以表示为：

在搜索空间内均匀随机初始化得到的。假定搜索空间的下限为xmin={x1,min,x2,min,…,xD,min}，上限为xmax={x1,max,x2,max,…,xD,max}，则初始群体中第i个个体的第j维可以表示为：

(2)

其中，randi,j(0,1)是均匀分布于0和1之间的随机数。

1.1.2 变异

在群体进化中，变异操作用于提高候选解的质量。在MMDE中，种群中的每个个体都通过结合DE/rand/1和CCDE[18]的多组变异策略进行更新。具体过程如下：

,

(3)

,

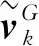
(5)

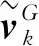
1.1.3 交叉

交叉操作用于实现种群中个体的基因交换从而提高种群的多样性。具体来说，交叉操作通过将当前候选解与其对应的变异向量混合，以构成一个试探向量。对于当前种群中的第i个候选解，试探向量的第j个分量可以表示为：

(6)

1.1.4 选择

选择操作用于确定候选解还是其对应的试探向量将被保留进入下一次迭代，这一操作是通过比较两者的目标函数值而实现的：

(7)

经过多次迭代，最终群体中目标函数值最小的个体即为优化问题的解。

1.2 带有横向约束的模型搜索空间设定方法

如图 2a所示，传统MMDE求解地震波阻抗反演问题时，每一道阻抗反演的搜索空间是通过在该道低频阻抗的基础上加减一个常数而设定的，可用如下公式表达：

,

(8)

考虑到地下介质具有横向连续性，相邻两道波阻抗之间应具有很强的空间相关性。为充分利用这一先验信息，我们提出一种新的带有横向约束的模型搜索空间设定方法。如图 2b所示，这一新方法利用旁道波阻抗反演结果约束本道波阻抗反演的搜索空间范围，具体可表示如下：

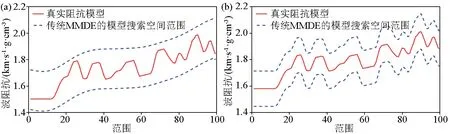
a—传统MMDE进行地震波阻抗反演时采用的模型搜索空间； b—本文所提出的带有横向约束的模型搜索空间

(9)

1.3 基于带有横向约束的全局优化地震波阻抗反演

地震波阻抗反演问题中，地震道d和波阻抗模型z可通过正演算子G(·)联系起来，如下式所示：

d=G(z)

,

(10)

具体来说，地震道d可以表示为地震子波与反射系数序列的褶积：

d=w⊗r

,

(11)

其中符号“⊗”表示褶积运算。反射系数序列与波阻抗的关系可以表示为：

(12)

其中，ri、zi、ρi和vi分别表示反射系数、阻抗、密度和纵波速度的第i个分量。

基于上述正演模型，地震波阻抗反演可描述为一个D维优化问题，该问题的目标函数可表示为：

,

(13)

其中，dobs和G(z)分别表示观测地震数据与合成地震数据。本文采用上述所提出的带有横向约束的多组变异差分进化算法优化式(13)所示的目标函数。

地震波阻抗反演中低频信息的引入对得到绝对波阻抗参数至关重要。在本文所提出方法中，每一个地震道的低频阻抗信息是在设定算法搜索空间范围时引入的。如式(9)所示，每一道的搜索空间范围除与旁道最优解相关外，还和本道的低频阻抗相关。在搜索空间范围内，算法通过迭代最小化式(13)所示的目标函数逐渐恢复波阻抗的中高频信息。

2 基于Marmousi II模型的算例分析

本节将所提出的理论方法应用于基于Marmousi II模型的实验算例并与传统方法进行对比。实验中使用的阻抗模型如图3a所示，该模型是通过对原始深度域Marmousi II模型进行深时转换及重采样得到的。该模型横向共有1 134道，每道长度为200 ms，采样间隔为2 ms。通过对真实阻抗模型每一道使用巴特沃兹低通滤波器提取其低频分量，构建了如图3b所示的低频阻抗模型作为反演的初始模型。实验中，我们采用主频为40 Hz的雷克子波生成地震数据，反演时假设子波已知。实验中分别采用所提出新方法与传统多组变异差分进化算法反演该模型的波阻抗，为保证对比的公平性，实验中两种对比方法除模型搜索空间初始化方式不同外，其它反演参数保持一致。实验结果如图 4、图5和表 1所示。

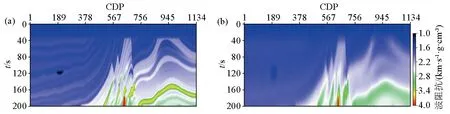
a—真实阻抗模型；b—反演使用的初始阻抗模型

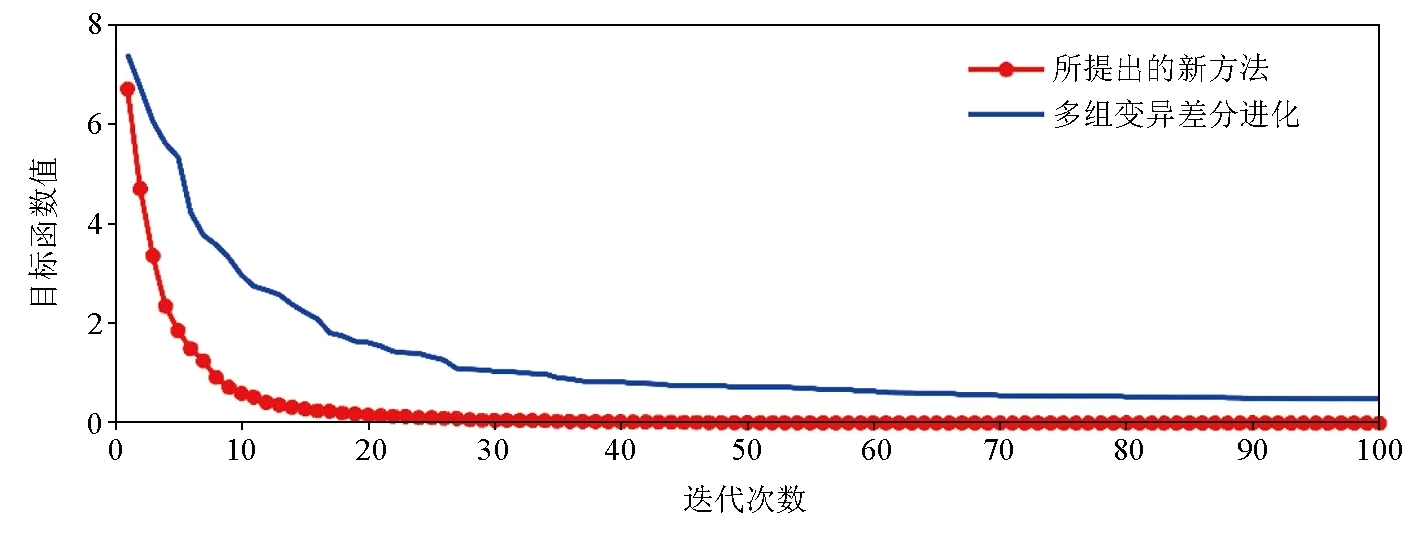
图4 对比所提出新方法与传统多组变异差分进化算法的收敛曲线

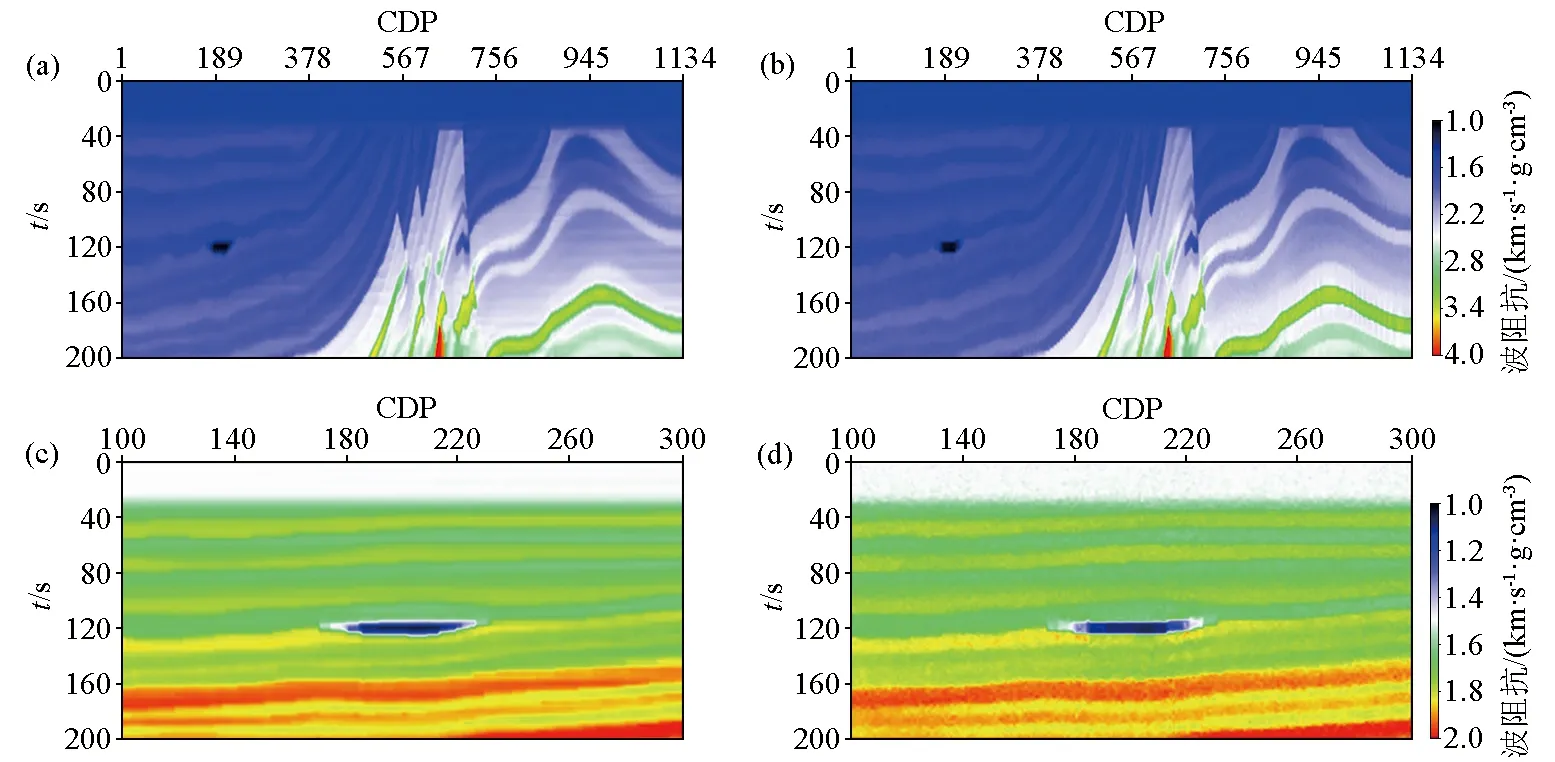
a—所提出新方法反演的阻抗模型；b—多组变异差分进化算法反演的阻抗模型；c、d—分别是a和b在CDP100～300处的阻抗模型放大对比

表1 定量化对比不同反演方法得到阻抗模型的质量

图4所示为两种反演方法的收敛曲线对比。在全部1134道数据中，我们选择第100道数据的反演过程进行对比。如图 4中蓝色曲线所示，传统多组变异差分进化算法在经过100次迭代后目标函数值从7.3936下降到0.4822，这说明多组变异差分进化算法可以在这一反演问题中收敛。与多组变异差分进化算法相比，本文所提出的理论方法的收敛速度更快，该方法经过100次迭代后目标函数值从6.6910下降到5.7949 e-5。此外，该方法仅需要12次迭代目标函数值就可以下降到0.4177，这一数值比多组变异差分进化算法100次迭代后的目标函数值还低。基于上述实验结果，可以看出所提出新方法具有显著优于传统多组变异差分进化算法的收敛速度，可在相同迭代次数的前提下得到更优的反演结果。

图5所示为两种反演方法构建的波阻抗模型。图5a所示为所提出新方法反演得到的波阻抗模型，该模型相对于真实模型的信噪比(signal-to-noise ratio，SNR)为36.0658 dB、结构相似性指数为0.9332。这些数据说明了该反演阻抗模型在阻抗结构以及数值上均和真实模型有很好的一致性。此外，图5c所示为所提出方法反演的波阻抗模型在CDP100～300处的放大图。从图中可见，反演阻抗模型具有良好的横向连续性。与所提出理论方法不同，图5b所示的传统多组变异差分进化算法反演的波阻抗模型精度不足。该模型相对于真实模型的信噪比SNR为33.2153 dB、结构相似性指数为0.8682，均显著低于所提出新方法的反演结果。此外，如图5d所示的反演结果表明传统多组变异差分进化算法的反演结果横向连续性差。具体来说，该反演阻抗模型充满噪声，真实模型中横向连续的地质结构在该模型中呈不连续状态。

综上所述，基于Marmousi II模型的实验算例验证了所提出理论方法的有效性，并验证了其相比于传统方法在效率和反演精度上的优势。

3 实际资料应用

本节将上述理论方法应用于胜利油田某工区实际三维地震资料。实验中采用整个三维工区的部分数据，这部分数据的范围是Inline 7080～7600，Crossline 3180～3450，时间方向1400～2450 ms。该数据的时间采样间隔为2 ms。目的层位于三角洲前缘，发育大量浊积岩砂体，具有良好的油气显示。图6a 所示为目标区连井地震剖面。目的层的主力储层砂体发育在T1、T2和T3层位之间，为典型的薄互层结构，砂层厚度薄单层在2～10 m，组合厚度4～20 m之间。此外，目的层砂体横向相变快，仅凭地震反射数据难以落实砂体展布边界。从地震波形上看(图6a)，由于薄互层干涉效应导致内部同相轴能量弱，横向连续性差，难以追踪。

采用本文提出的阻抗反演方法对该工区三维地震数据进行处理。这里，反演使用的子波是通过统计的方法从地震数据中提取。图6b为采用本文所提出方法计算的波阻抗连井剖面。根据测井解释成果，我们知道目标层段砂岩表现为阻抗高值，泥岩表现为阻抗低值。井点位置黑色曲线展示的是利用测井数据计算的波阻抗曲线。我们也将测井岩性解释结果覆盖到井点处。从岩性解释结果中不难看出，T1～T2层段发育厚度非常薄的砂体，在地震剖面上表现为不连续的同相轴(图6a)，难以分辨薄砂体的组合关系与横向分布范围。利用本文所提出方法计算的波阻抗结果虽然无法刻画T1～T2层段之间5 m以下的薄层砂体(图6b中红色箭头指示)，但对于厚度较大的砂体则能清晰地展示砂体横向展布范围，并且与井数据计算的波阻抗有良好的匹配关系(图6b中蓝色箭头指示)。T2～T3层段内部发育组合厚度较厚的砂体，采用本文方法计算的波阻抗能够很好地表征其内部的砂体展布规律，且在井点处能很好地匹配测井计算结果。图7为本文方法计算结果的三维展示。为了更好的对比效果，我们沿图6b所示的T2_1层位做沿层切片，得到图8a所示的沿层阻抗。进一步与同层位井插值得到的砂地比(图8b)进行对比，不难看出高阻抗区域对应高砂地比，低阻抗区域对应低砂地比。这进一步验证了本文方法的有效性。

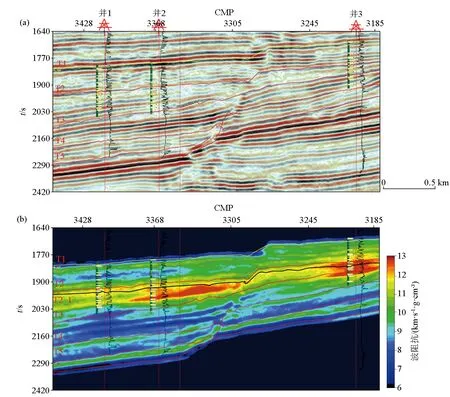
a—地震剖面；b—波阻抗剖面；井点位置处黑色曲线为利用测井数据计算的波阻抗

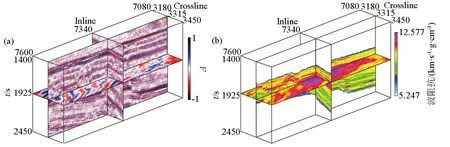
a—胜利油田某工区三维叠后地震资料；b—所提出理论方法反演的波阻抗数据体

a—反演波阻抗模型沿T2_1层位的切片；b—井插值砂地比剖面

4 结论及讨论

1) 带有横向约束的模型搜索空间设定方法在本文的全局优化波阻抗反演中起到了保证反演结果横向连续性和提升反演效率的效果。

2) 带有横向约束的全局优化波阻抗反演方法进行了实际应用，反演的波阻抗能够很好地表征储层内部的砂体展布规律，且在井点处与测井结果匹配度高。验证了本研究的实用性。

3) 进一步提升全局优化波阻抗反演方法的效率，是下一步研究的方向。