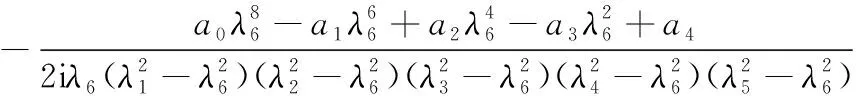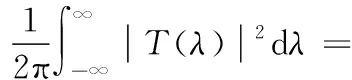基于H2范数的弹性基础上接地负刚度动力吸振最优参数研究
2023-01-03苏智伟郑智伟张啸涵黄修长
刘 冬, 苏智伟,2, 郑智伟, 杨 咏, 张啸涵, 李 杨, 黄修长,
(1. 上海交通大学 先进技术与装备研究院 机械系统与振动国家重点实验室,上海 200240; 2. 五邑大学 智能制造学部,广东 江门 529020; 3. 船海特装和动力系统国家工程中心,上海 200240)
将负刚度单元引入系统并经合理匹配设计后,振动系统能具有固有频率低、隔振带宽宽、隔振效果好等优点。接地负刚度动力吸振技术是其中之一。接地负刚度动力吸振最早由Antoniadis等[1-2]于2015年提出,即在常规吸振器的吸振子与地基之间引入一个负刚度单元。相比于常规动力吸振,接地负刚度动力吸振经合理的参数优化匹配后,可在不需要较大吸振质量的前提下,在特定频段内实现无谐振峰宽频带振动控制,有效解决常规动力吸振的振动控制效果与吸振质量间的矛盾。
国内外学者对接地负刚度动力吸振的最优参数开展了相关研究。Shen等[3-4]提出了多种接地负刚度动力吸振形式,采用数值方法或解析法获得了最优阻尼比和最优频率比等参数。研究结果表明,相比于常规动力吸振器,接地负刚度动力吸振器在简谐激励和随机激励下对主系统位移传递率的控制效果均表现得更加良好。Zhou等[5]针对两种构型的接地负刚度动力吸振,利用不动点法和稳定性最大准则分别推导了系统的最优参数,并结合稳定性条件给出了负刚度值的取值范围。Li等[6]将负刚度动力吸振与惯容单元相结合,提出了新形式的动力吸振模型,并推导了模型的封闭解,结果表明惯容单元和负刚度单元在系统中均发挥了放大质量效应。为进一步降低低频段内共振峰的幅值,代晗等[7]将时滞反馈控制引入接地负刚度动力吸振,并进行了等峰参数优化。陈杰等[8]利用惯容负刚度动力吸振器抑制梁的横向振动,推导了最优系统参数,并讨论了质量比对系统最优参数的影响。
国内外学者针对工程实际中的接地负刚度开展了动力学建模。Zhou等[9]将接地负刚度动力吸振应用于浮置板轨道减振,建立了浮置板轨道的有限元模型,利用接地负刚度动力吸振对浮置板的一阶弯曲模态进行控制。Liu等[10]采用接地负刚度动力吸振来降低压载轨道的振动与声辐射,计算结果表明相比于常规动力吸振器,采用接地负刚度动力吸振能有效提高轨道的振动能量和声辐射衰减。Kapasakalis等[11]将接地负刚度动力吸振应用于风机的减振,仿真结果表明其能显著增加系统的有效阻尼,降低风载作用下风机的动力学响应。Lin等[12]基于接地负刚度动力吸振提出了一种新形式的力学超材料构型,用于指导设计地震隔震系统。Sapountzakis等[13]开展了接地负刚度动力吸振用于地震波激励下桥梁结构的抗震分析,分析过程中考虑了桥墩的贡献,结论表明基于接地负刚度动力吸振的减震方案在理论上能有效替代传统的桥梁隔震支座。
以上关于接地负刚度动力吸振的研究集中在理论建模获取最优参数以及简单模型应用方面,理论建模时考虑接地负刚度动力吸振在刚性基础上的情况。而实际工程中往往是弹性基础,弹性基础与主系统的耦合会改变主系统固有特性,以及接地负刚度动力吸振的动力学特性,使得基于刚性基础得到的最优参数不再适用。本文针对实际工程中常常出现的弹性基础,基于H2范数推导了接地负刚度动力吸振的最优参数。
1 动力学建模及最优参数推导
1.1 弹性基础接地负刚度动力吸振动力学模型
弹性基础上的接地负刚度动力吸振系统动力学模型可表示一个三自由度系统,如图1所示。Mp和kp为弹性基础的等效模态质量和等效模态刚度。MA为主系统质量;ks为主系统刚度;m,ke和c分别为Voigt型动力吸振器的质量、刚度和阻尼;kn为负刚度元件的负刚度(假设kn不随频率和相对位移幅值变化);F为施加在主系统质量MA上的外激励力;FT为传递到弹性基础的力;x和y分别为MA和m的位移响应;z为弹性基础质量相对地面的位移响应。

图1 考虑弹性基础的接地负刚度动力吸振动力学模型Fig.1 Dynamic modelling of DVA with negative stiffness considering flexible foundation
对图1所示模型建立运动微分方程
(1)
引入负刚度比p、吸振质量比μ、基础质量比μp、吸振频率比ν、基础频率比νp以及阻尼比ξ等无量纲参数
假设系统的稳态响应为[x,y,z]T=[X,Y,Z]Tejωt,代入运动微分方程,可求得X,Y,Z的响应表达式为
(3)
定义到基础的力传递率为传递至基础的作用力与主系统外激励力的比值
(4)
Γ=λ4μ-λ2μ2v2-λ2μv2-μμpλ6+λ4μ2v2μp+λ4μv2μp+
1.2 基于H2范数优化准则的参数优化
对于弹性基础上的动力吸振最优参数问题,由于基础的阻抗为频率的函数,与主系统相关的不动点处的幅值不再和频率无关,此时无法采取常规不动点法对主系统进行动力吸振匹配设计。以力传递率的H2范数最小为优化目标,可得弹性基础上接地负刚度动力吸振的最优参数。力传递率T的H2范数可定义为
(6)

(7)
将无量纲力传递率表达式代入可得

(8)
利用留数定理,可将积分表达式化简为多项式表达式(系数a0~a4,b1~b5及后续推导过程可详见附录A),如式(19)所示
(9)
为得到弹性基础负刚度动力吸振的最优频率比vopt和最优阻尼比ξopt,令式(9)分别对v和ξ的偏导等于0,得到最优频率比vopt和最优阻尼比ξopt的表达式

(11)
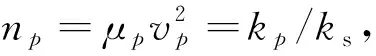

(12)

(13)
可见,以控制外激励到基础的力传递率为目标,接地负刚度动力吸振的最优阻尼比和最优频率比仅与吸振质量比μ和基础刚度比np有关,与基础质量比无关。
1.3 稳定性分析
对于弹性基础上的接地负刚度动力吸振,由于负刚度单元的存在,系统存在稳定性问题。采取刚性基础中稳定性分析的方法,根据Routh-Hurwitz判据来进行判别。当系统所有极点均处于复平面左侧时(具有负实部),系统稳定。将力传递率的分母多项式改写为
D(s)=q0s6+q1s5+q2s4+q3s3+q4s2+q5s+q6,s=jλ
(15)
其中
q0=μμp,
q1=2μ(μ+1)vξμp,
(16)
结合Routh-Hurwitz判据,以及式中根号内表达式大于0的条件,经推导得到的系统稳定性条件如下

(17)
将多个关于p的不等式取交集,可得关于负刚度比p的稳定性条件为
(18)
可见当优化目标为传递到基础的力传递率时,关于负刚度比p的稳定性条件仅与吸振质量比μ有关,与基础的特性无关。
2 参数影响规律分析
图2(a)和图2(b)分别给出了μ=0.01,p=-0.02时最优频率比vopt和最优阻尼比ξopt随基础刚度比np的变化规律。可见,接地负刚度动力吸振的最优频率比随着基础刚度比的增加而增加,最优阻尼比随着基础刚度比的增加而减小。接地负刚度动力吸振的最优吸振刚度要大于Voigt型动力吸振的最优吸振刚度,而当基础刚度比0

图2 最优参数随基础刚度比的变化规律Fig.2 Optimal parameters of vopt and ξopt with varying np
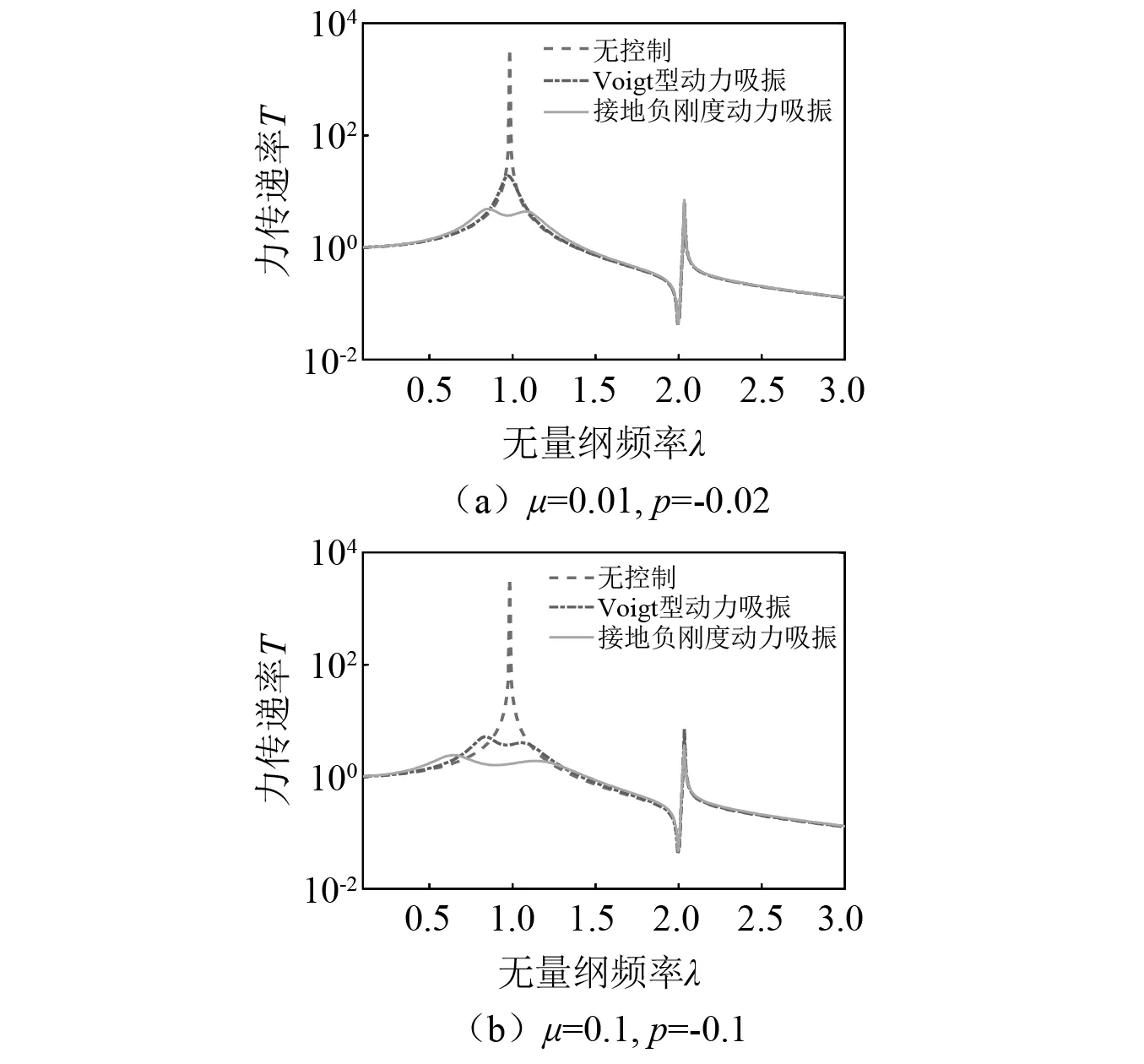
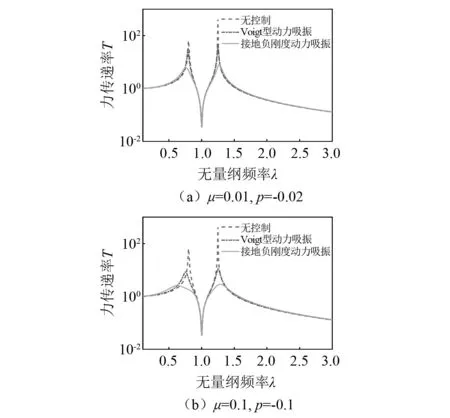
为对比弹性基础上接地负刚度动力吸振的振动控制效果,图3给出了接地负刚度动力吸振和Voigt型动力吸振在最优参数下的H2范数优化的目标函数Ia的对比,其中Ia表征着整个频段内振动总能量。图3中横坐标为基础和主系统的刚度比np,纵坐标为Ia/Ia_nodva(定义为Ia幅值下降相对量),即控制后和控制前目标函数Ia的比值。对比图3(a)、图3(b)两图可知,增大吸振质量比和负刚度比绝对值,能增强Voigt型动力吸振和接地负刚度动力吸振的振动抑制效果。不同负刚度比和质量比情况下,接地负刚度动力吸振的振动抑制效果要远优于Voigt型动力吸振,且负刚度动力吸振对应的幅值下降相对量几乎不受基础刚度比变化的影响。这说明当考虑弹性基础时,接地负刚度动力吸振在最优参数下的振动抑制效果对基础刚度比的变化不敏感。当基础的状态发生较大改变时,接地负刚度动力吸振仍可实现极佳的振动抑制效果。Voigt型动力吸振在0 图3 最优参数下目标函数Ia随基础刚度比的变化规律Fig.3 Performance index Ia under optimal parameters with varying np 尽管给定质量比μ、负刚度比p时,最优参数下的目标函数Ia值仅与基础刚度比np有关,但对于本文的控制目标,即弹性基础上外激励到基础的力传递率,依然同时取决于基础质量比μp和基础频率比vp。为进一步验证在考虑不同基础质量比和频率比时,基于H2范数最小推导得到的最优参数是否依然成立,并综合分析基础的动力学特性对力递率特性的影响,图4~图6给出了不同基础质量比和频率比下的力传递率幅频曲线,并将结果与推导得到的Voigt型动力吸振最优参数下的结果进行了对比。 图4给出了基础质量比μp=10,基础频率比vp=2时的力传递率曲线,此时基础刚度比np=40。这组参数下基础的固有频率远离主系统固有频率(λ1=0.98,λ2=2.02),两个系统耦合小。当质量比μ=0.01、负刚度比p=-0.02时,Voigt型动力吸振的最优频率比和最优阻尼比分别为0.980和0.093,接地负刚度动力吸振的最优频率比和最优阻尼比分别为1.721和0.097;当质量比μ=0.1、负刚度比p=-0.1时,Voigt型动力吸振的最优频率比和最优阻尼比分别为0.920和0.172,接地负刚度动力吸振的最优频率比和最优阻尼比分别为1.349和0.228;由于两个系统耦合小,因此传递率的结果和刚性基础的结果类似,接地负刚度动力吸振在最优参数下能大幅降低主系统共振区域的振幅,且拓宽了吸振带宽,有着近似无谐振峰的控制效果。且接地负刚度动力吸振的性能对吸振质量不敏感,当吸振质量比较小时,接地负刚度动力吸振相较于Voigt型动力吸振的优势更加明显。 图4 μp=10, vp=2时,最优参数下接地负刚度动力吸振与Voigt型动力吸振力传递率对比Fig.4 Comparison of force transmissibility under optimal parameters between DVAGNS and Voigt type DVA under μp=10, vp=2 图5给出了当基础质量比μp=5,基础频率比vp=1时的力传递率曲线,此时基础刚度比np=5。这组参数下基础的固有频率与主系统固有频率相同,两个系统耦合强。当质量比μ=0.01、负刚度比p=-0.02时,Voigt型动力吸振的最优频率比和最优阻尼比分别为0.906和0.229,接地负刚度动力吸振的最优频率比和最优阻尼比分别为1.682和0.145;当质量比μ=0.1、负刚度比p=-0.1时,Voigt型动力吸振的最优频率比和最优阻尼比分别为0.850和0.275,接地负刚度动力吸振的最优频率比和最优阻尼比分别为1.313和0.259。由于基础和主系统的固有频率相同,对应耦合系统的两个固有频率均离主系统固有频率较远(λ1=0.79,λ2=1.24)。此时Voigt型动力吸振的控制效果有限,力传递率曲线未出现明显的双峰特征,但接地负刚度动力吸振依然有着较好的振动抑制效果,且随着质量比和负刚度比的绝对值增加,抑振能力增加。当质量比μ=0.1、负刚度比p=-0.1时,在主系统共振段依然体现出了近似无谐振峰的特征,同时在基础共振频段内也有着较好的控制效果。 图5 μp=5,vp=1时,最优参数下接地负刚度动力吸振与Voigt型动力吸振力传递率对比Fig.5 Comparison of force transmissibility under optimal parameters between DVAGNS and Voigt type DVA under μp=5,vp=1 图6给出了基础质量比μp=0.5,基础频率比vp=0.8时的力传递率曲线,此时基础刚度比np=0.32。这组参数下基础刚度小于主系统刚度,且基础质量小于主系统质量。由于基础和主系统串联,耦合系统的动力学特性主要取决于小刚度系统,即弹性基础对耦合系统的力传递率特性有较大影响。当质量比μ=0.01、负刚度比p=-0.02时,Voigt型动力吸振的最优频率比和最优阻尼比分别为0.488和0.887,接地负刚度动力吸振的最优频率比和最优阻尼比分别为2.093和0.218;当质量比μ=0.1、负刚度比p=-0.1时,Voigt型动力吸振的最优频率比和最优阻尼比分别为0.458和0.917,接地负刚度动力吸振的最优频率比和最优阻尼比分别为1.140和0.402;此时,在基础的质量和刚度均小于主系统时,Voigt型动力吸振在所给的两种吸振质量比情况下均几乎已无控制效果,接地负刚度动力吸振虽控制效果略有所折扣,但依然能同时有效降低耦合系统两个共振频段的峰值。综合图4~图6的结果可知,基于H2范数优化准则得到的弹性基础上接地负刚度动力吸振的最优参数,在考虑不同基础力学特性时均能有效抑制主系统共振段幅值。 图6 μp =0.5, vp=0.8时,最优参数下接地负刚度动力吸振与Voigt型动力吸振力传递率对比Fig.6 Comparison of the force transmissibility under optimal parameters between DVAGNS and Voigt type DVA under μp =0.5, vp=0.8 图7 不同基础质量比和刚度比下随机激励传递力时间历程对比Fig.7 Comparison of the time history of transmitted force between DVAGNS and Voigt type DVA under different characterisitcs of the flexible foundation 采取H2范数优化准则对弹性基础上的接地负刚度动力吸振器进行了参数优化,获得了其最优参数解析表示式。开展了参数影响规律分析,在简谐激励和随机激励下验证了接地负刚度动力吸振器的吸振性能。得到以下结论: (1)考虑弹性基础时,以控制外激励到基础的力传递率为目标时,通过H2范数优化准则得到的弹性基础上的接地负刚度动力吸振最优参数仅取决于吸振质量比和基础与主系统的刚度比,而与基础的质量比无关。 (2)考虑弹性基础时,最优参数下接地负刚度动力吸振同样能以小质量比的代价在主系统共振频段和基础共振频段内实现较好的振动传递控制效果。且当基础与主系统耦合强时,接地负刚度动力吸振依然能实现有效控制,但此时Voigt动力吸振已基本失效。 附录A最优参数推导过程 正文中式(8)分子分母的系数如下 a0=1, b1=2(μ+1)vξ, (A.1) 为保证系统的稳定性,b1~b6应均为非负值。式(8)的分母可改写为 IaDen=(λ+jλ1)(λ+jλ2)(λ+jλ3)(λ+jλ4)(λ+jλ5)(λ+jλ6)· (λ-jλ1)(λ-jλ2)(λ-jλ3)(λ-jλ4)(λ-jλ5)(λ-jλ6) (A.2) 不妨假设驻点λ1~λ6均为正。将式(A.2)展开,并与式(A.1)对比可得 b1=λ1+λ2+λ3+λ4+λ5+λ6, b2=λ1λ2+λ1λ3+λ1λ4+λ1λ5+λ1λ6+λ2λ3+λ2λ4+λ2λ5+ λ2λ6+λ3λ4+λ3λ5+λ3λ6+λ4λ5+λ4λ6+λ5λ6, b3=λ1λ2λ3+λ1λ2λ4+λ1λ2λ5+λ1λ2λ6+λ1λ3λ4+λ1λ3λ5+λ1λ3λ6+λ1λ4λ5+λ1λ4λ6+λ1λ5λ6+λ2λ3λ4+λ2λ3λ5+λ2λ3λ6+λ2λ4λ5+λ2λ4λ6+λ2λ5λ6+λ3λ4λ5+λ3λ4λ6+λ3λ5λ6+λ4λ5λ6, b4=λ1λ2λ3λ4+λ1λ2λ3λ5+λ1λ2λ3λ6+λ1λ2λ4λ5+λ1λ2λ4λ6+ λ1λ2λ5λ6+λ1λ3λ4λ5+λ1λ3λ4λ6+λ1λ3λ5λ6+λ1λ4λ5λ6+λ2λ3λ4λ5+λ2λ3λ4λ6+λ2λ3λ5λ6+λ2λ4λ5λ6+λ3λ4λ5λ6, b5=λ1λ2λ3λ4λ5+λ1λ2λ3λ4λ6+λ1λ2λ3λ5λ6+λ1λ2λ4λ5λ6+ λ1λ3λ4λ5λ6+λ2λ3λ4λ5λ6, b6=λ1λ2λ3λ4λ5λ6 (A.3) 式(A.2)存在12个极点,即式(A.2)等于0时λ所取的值。复平面上半平面存在6个孤立奇点(满足b1,b2,b3,b4,b5,b6>0的情况下) λ=iλ1,iλ2,iλ3,iλ4,iλ5,iλ6 (A.4) 由留数定理可求无穷积分 (A.5) 各个极点的留数为 Res[fn;iλ1]=(λ-iλ1)fn(iλ1)= Res[fn;iλ2]=(λ-iλ2)fn(iλ2)= Res[fn;iλ3]=(λ-iλ3)fn(iλ3)= Res[fn;iλ4]=(λ-iλ4)fn(iλ4)= Res[fn;iλ5]=(λ-iλ5)fn(iλ5)= Res[fn;iλ6]=(λ-iλ6)fn(iλ6)= (A.6) 将式(A.6)代入式(A.5)可求得无穷积分 (A.7) 其中 将式(A.3)与式(A.1)代入式(A.7),目标函数表达式(9)中的分子和分母可以表示为 式(9)分别对v和ξ求偏导等于0,即 (A.8) 可得出如下方程组 (A.9) 求解方程组(A.9),可得弹性基础上接地负刚度动力吸振的最优频率比vopt和最优阻尼比ξopt的解析表达式,如式(10)、式(11)所示。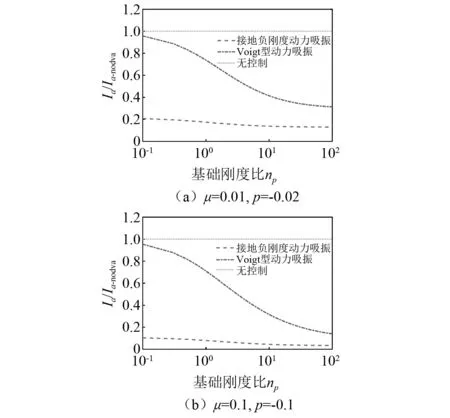


3 结 论