具有非线性能量阱的弹性边界约束轴向载荷梁结构动力学行为研究

赵雨皓， 杜敬涛， 张树奇， 刘 杨， 陈依林

(1. 哈尔滨工程大学 动力与能源工程学院, 哈尔滨 150001; 2. 北京京能国际能源技术有限公司, 北京 100041)

轴向载荷梁作为一种基本单元广泛应用于船舶轴系结构振动分析中，其中轴向载荷通常由动力设备引入。在工程中，轴向载荷梁结构在外部激励下发生不利振动。为降低轴向载荷梁结构的过大振动，研究其动力学行为与振动控制方式就显得尤为重要。

近年来，众多学者采用傅里叶级数研究不同边界条件下梁结构振动特性和动力学行为[1-7]。在船舶轴系振动分析中，支承轴承通常被简化为旋转、平动支撑刚度。传统傅里叶级数由于其边界不连续性难以应用于具有一般边界轴系结构的振动特性分析中。为提高傅里叶级数的工程适用性，Li[8]提出边界光滑傅立叶级数用于研究具有一般边界约束的梁结构振动特性。在此基础上，众多学者采用光滑边界傅里叶级数研究了弹性边界约束梁结构的振动特性[9-11]。考虑到工程中轴向载荷的存在，Xu[12-13]等利用边界光滑傅里叶级数和能量原理建立具有一般边界约束的轴向载荷梁结构的振动特性分析模型。

非线性能量阱作为一种有效的被动振动控制手段由Vakakis[14]提出。非线性能量阱具有轻质、宽频以及能量靶向传递特性，自提出以来受到了国内外学者的广泛关注。Georgiades等[15]研究了具有非线性能量阱的Euler-Bernoulli梁动力学行为。Samani等[16]通过最大振动幅值和耗能估计非线性能量阱的吸振性能。Ahmadabadi等[17-18]研究了具有非线性能量阱的悬臂梁结构非线性控制。Kani等[19-20]研究了具有非线性能量阱和经典边界条件梁结构振动控制问题。Zhang等[21]研究了具有非线性能量阱的轴向运动梁结构振动控制，表明非线性能量阱对梁结构振动抑制具有良好的效果。Fang等[22]设计了一种单稳/双稳非线性能量阱控制具有阻尼层悬臂梁结构的振动。李响[23]、王闯[24]和贺腾[25]分别采用解析与数值方法研究了非线性能量阱对梁结构的振动控制效果。鲁正等[26]结合现有研究，综述了非线性能量阱技术在振动控制中的应用与优势。姚永玉等[27]分析了非线性能量阱对悬臂梁结构的振动抑制特性。Zhang等[28]研究了边界非线性能量阱对梁结构自由、强迫响应的振动抑制效果。值得注意的是上述研究多是在特定边界下开展，忽略梁结构边界处旋转约束，当边界条件改变时，需对模型进行重新建立。此外，上述研究未考虑工程中常见的轴向载荷且未充分研究非线性能量阱对梁结构动力学响应、减振效果的影响规律。因此，建立具有非线性能量阱的弹性边界约束轴向载荷梁结构振动分析模型具有重要意义。

本文研究具有非线性能量阱的弹性边界约束轴向载荷梁结构动力学响应与减振特性规律。采用Galerkin截断法(Galerkin truncation method，GTM)预报具有非线性能量阱的轴向载荷梁结构动力学响应。在Galerkin离散化过程中，具有线弹性边界的轴向载荷Euler-Bernoulli梁结构的模态函数作为Galerkin截断法的权函数和试函数。采用谐波平衡法(harmonic balance method,HBM)验证Galerkin截断法的计算结果。在上述基础上，研究非线性能量阱对梁结构动力学响应、减振效果的影响。

1 理论模型

如图1所示，考虑具有非线性能量阱的弹性边界约束轴向载荷梁结构横向振动问题。在梁结构两端引入约束弹簧对边界条件进行模拟；kL与kR分别为左、右边界平动刚度；KL与KR分别为左、右边界旋转刚度；CL与CR分别为左、右边界黏性阻尼。梁结构模型为Euler-Bernoulli梁；E，L，ρ，I与S分别为其杨氏模量、长度、密度、惯性矩及截面积；P为作用在梁结构上的轴向载荷，其中拉力载荷为负，压力载荷为正；F(x,t)为作用在梁结构上的外部激励，在本文研究中，外部激励为简谐激励力，其形式为F(x,t)=δ(x-xF)·F0sin(ωt)。其中xF为外部激励作用位置，F0为外部激励幅值。非线性能量阱由黏性阻尼CNES，质量mNES与非线性刚度knNES组成。本文考虑具有惯性效应的非线性能量阱，非线性能量阱的有效惯性质量(bN)为惯性系数(bc)与非线性能量阱质量(mNES)的乘积。u(x,t)与uNES分别为梁结构的横向振动位移与非线性能量阱的振动位移。

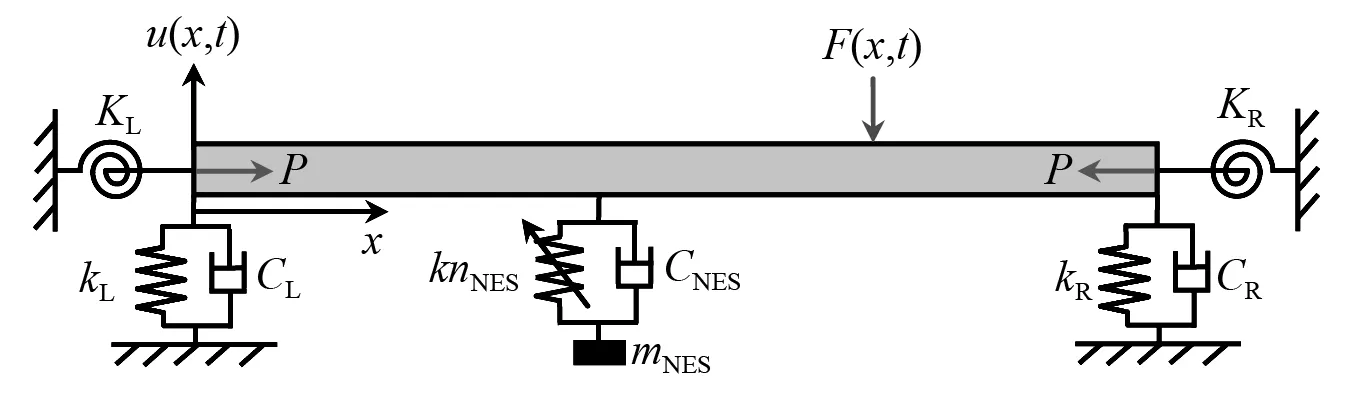
图1 具有非线性能量阱的弹性边界约束轴向载荷梁结构振动分析模型Fig.1 Vibration analysis model of an axially loaded beam structure with a nonlinear energy sink and elastic boundary restraints

根据牛顿第二定律推导梁结构、非线性能量阱的动力学控制方程与振动系统边界条件。梁结构左端点边界条件为

(1)

(2)

右端边界条件为

(3)

(4)

式(5)为非线性能量阱的动力学控制方程；式(6)为梁结构动力学控制方程。

knNES[uNES-u(xNES)]3=0

(5)

本文采用Galerkin截断法预报具有非线性能量阱的弹性边界约束轴向载荷梁结构的动力学特性。在Galerkin截断法中，选取一组满足边界条件的函数作为权函数与试函数，实现梁结构系统动力学控制方程的离散。考虑到边界阻尼的存在，通过狄利克雷函数将边界阻尼引入梁结构动力学控制方程中此时边界条件与梁结构动力学控制方程被改写为式(7)、式(8)与式(9)。由式(7)与式(8)可知，梁结构振动系统具有线弹性边界条件，因此具有弹性边界约束的轴向载荷梁结构系统的模态函数被选取为Galerkin截断法中的权函数与试函数。

2 Galerkin截断法与求解

在本文分析中，根据模态叠加原理，梁结构振动系统的横向振动位移展开为如下形式

(10)

式中：φi(x)为具有弹性边界约束的轴向载荷梁结构振动系统的第i阶模态函数；N为截断数；具有弹性边界约束的轴向载荷梁结构振动系统的模态函数通过边界光滑傅里叶级数与能量法求解得到。

在上述基础上，将式(10)代入式(5)，得到非线性能量阱动力学方程的具体表达形式，如式(11)所示。将式(10)代入式(9)，并对其进行Galerkin离散，得到梁结构振动系统的残差方程，其中第m阶残差方程的形式如式(12)所示。

(11)

(12)

将梁结构振动系统的第m阶残差方程简化为如下形式

Rm1+Rm2+Rm3+Rm4+Rm5+Rm6+Rm7+Rm8+Rm9=0

(13)

式(13)中各项的具体形式为

(14)

(15)

(16)

(17)

Rm5=ψm(xF)F0sin(ωt)

(18)

(19)

(20)

(22)

将式(13)中的加速度项移至等式的另一侧，式(13)改写为

Rm1=-(Rm2+Rm3+Rm4+Rm5+Rm6+Rm7+Rm8+Rm9)

(23)

根据式(14)，Rm1可以展开为

(24)

在上述基础上，将梁结构振动系统的残差方程整理为矩阵的形式，即

(25)

将式(11)与式(25)整理为标准矩阵形式，即

(26)

式中，RNES的具体表达式为

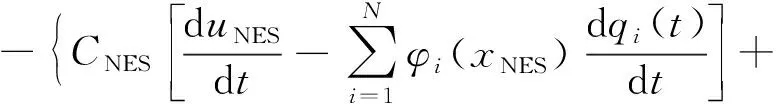
(27)

式(26)可通过4阶龙格-库塔算法直接求解，将求解结果代入式(10)即可得到具有非线性能量阱与弹性边界约束的轴向载荷梁结构振动系统任意点的动力学响应。

3 数值结果与分析

按照上述理论推导，对具有非线性能量阱的弹性边界约束轴向载荷梁结构振动系统进行编程仿真。首先验证本文模型在预报梁结构振动系统动力学响应时的准确性和可靠性。在此基础上，研究非线性能量阱参数对梁结构振动系统减振、动力学特性的影响规律。

3.1 模型验证

本节采用Galerkin截断法预报具有非线性能量阱的弹性边界约束轴向载荷梁结构的动力学响应。采用谐波平衡法所得到的梁结构动力学响应与Galerkin截断法所得结果进行对比，验证本文模型的正确性。在此基础上，研究截断数对Galerkin截断法所得结果的影响。表1列出了梁结构材料参数、几何参数与边界约束弹簧刚度值。表2给出了非线性能量阱的参数值。外部激励幅值F0=10 N，外部激励位置xF=0。

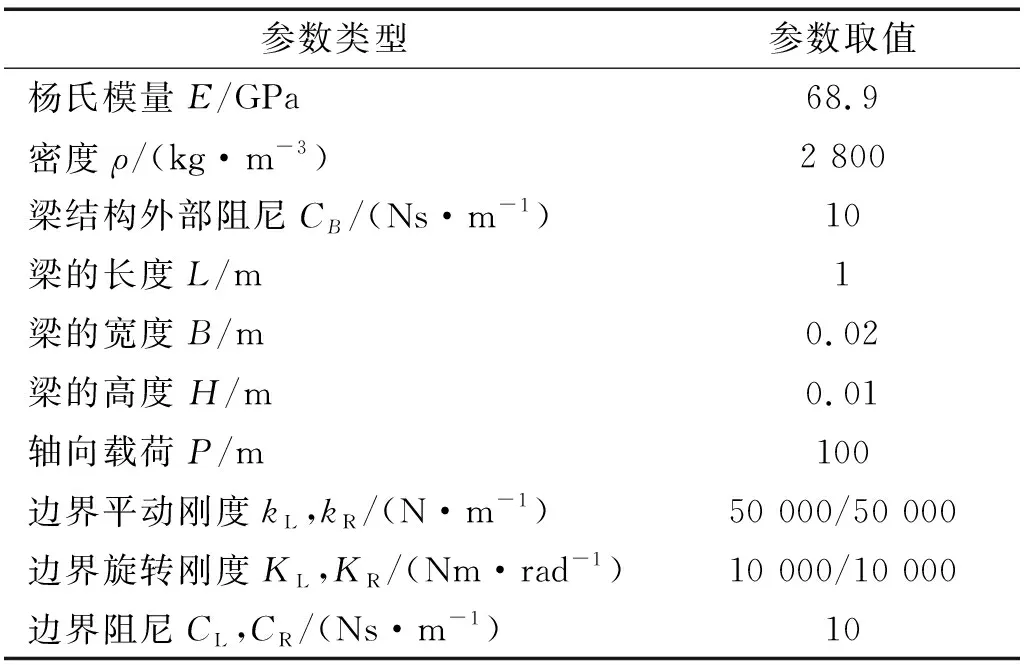
表1 梁结构材料、几何与边界参数值Tab.1 Material, geometric and boundary parameters of beam structure

表2 非线性能量阱参数值Tab.2 Parameters of the nonlinear energy sink

首先验证基于Galerkin截断法所构建模型的正确性。Galerkin截断法的计算参数取为N=M=2。为消除瞬态响应，选取0～420Te为计算域，其中Te为简谐外激励作用周期。选取400～420Te的结果作为稳态周期结果。4阶龙格-库塔算法的初始值取为

(28)

图1为采用谐波平衡法与Galerkin截断法得到的具有非线性能量阱与梁结构振动系统端点处的动力学响应。由图1可知，两种方法所得结果吻合良好，验证了Galerkin截断法在求解本文模型时的正确性。

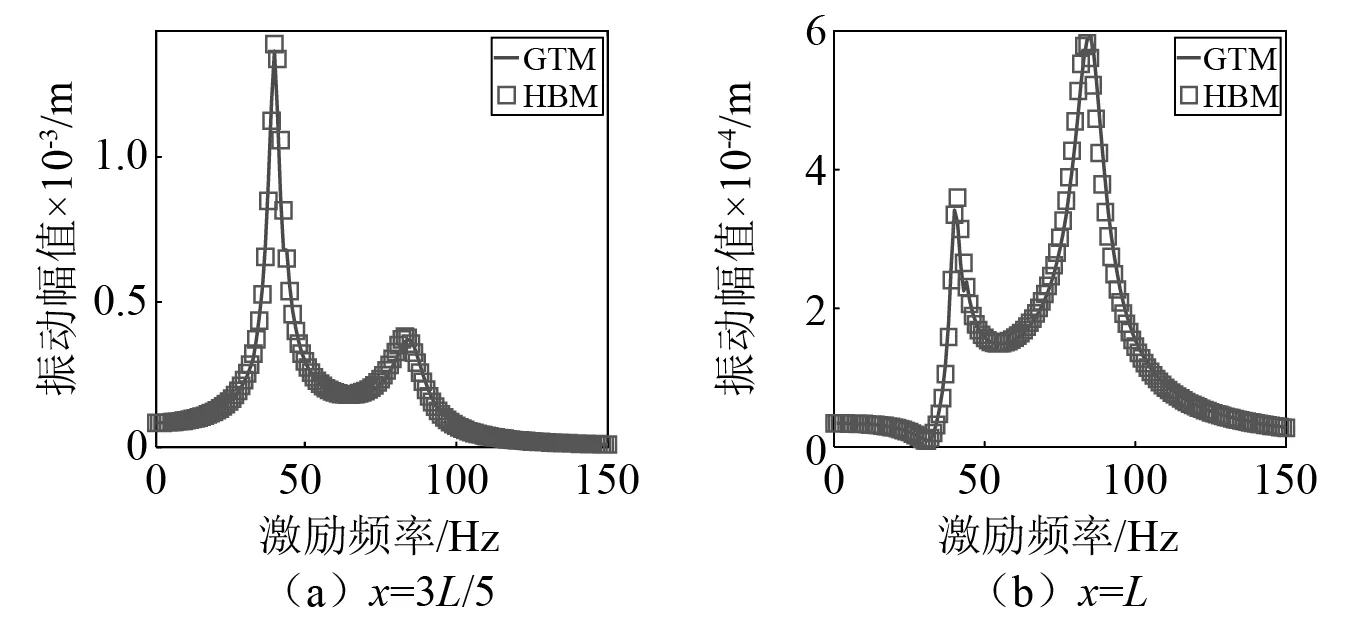
图2 梁结构稳态幅频响应曲线Fig.2 Stable steady-state amplitude-frequency response curves of beam structure

图3给出当截断数分别为2，4和6时梁结构的稳态幅频响应曲线。由图3可知，当截断数为4和6时，梁结构的动力学响应结果已经收敛。因此，在后续研究中，选取Galerkin截断法的截断数为N=M=4。

图3 不同截断数下梁结构稳态幅频响应曲线Fig.3 Stable steady-state amplitude-frequency response curves of beam structure with different truncated terms

3.2 非线性能量阱与激励位置对梁结构振动行为的影响

本节研究非线性能量阱以及激励位置对梁结构振动行为的影响。梁结构边界条件取值为kL=50 000 N/m,kR=500 N/m,KL=10 000 Nm/rad,KR=100 Nm/rad,CL=CR=0。梁结构参数、外部激励参数与3.1节中相同。

首先研究非线性能量阱参数对梁结构动力学响应的影响。图4研究非线性能量阱对梁结构端点处稳态响应的振动抑制效果。非线性能量阱参数取值为kNES=1×109N/m,CNES=1×10 Ns/m,mNES=0.001 kg,xNES=0.2 m。由图4可知，非线性能量阱的存在能够有效抑制梁结构在第2阶、第3阶主共振区振动。在第2阶主共振区处非线性能量阱对左、右端点的吸振效果分别为41.9 %与46.3%；在第3阶主共振区处非线性能量阱对左、右端点的吸振效果分别为66.0%与65.9%。

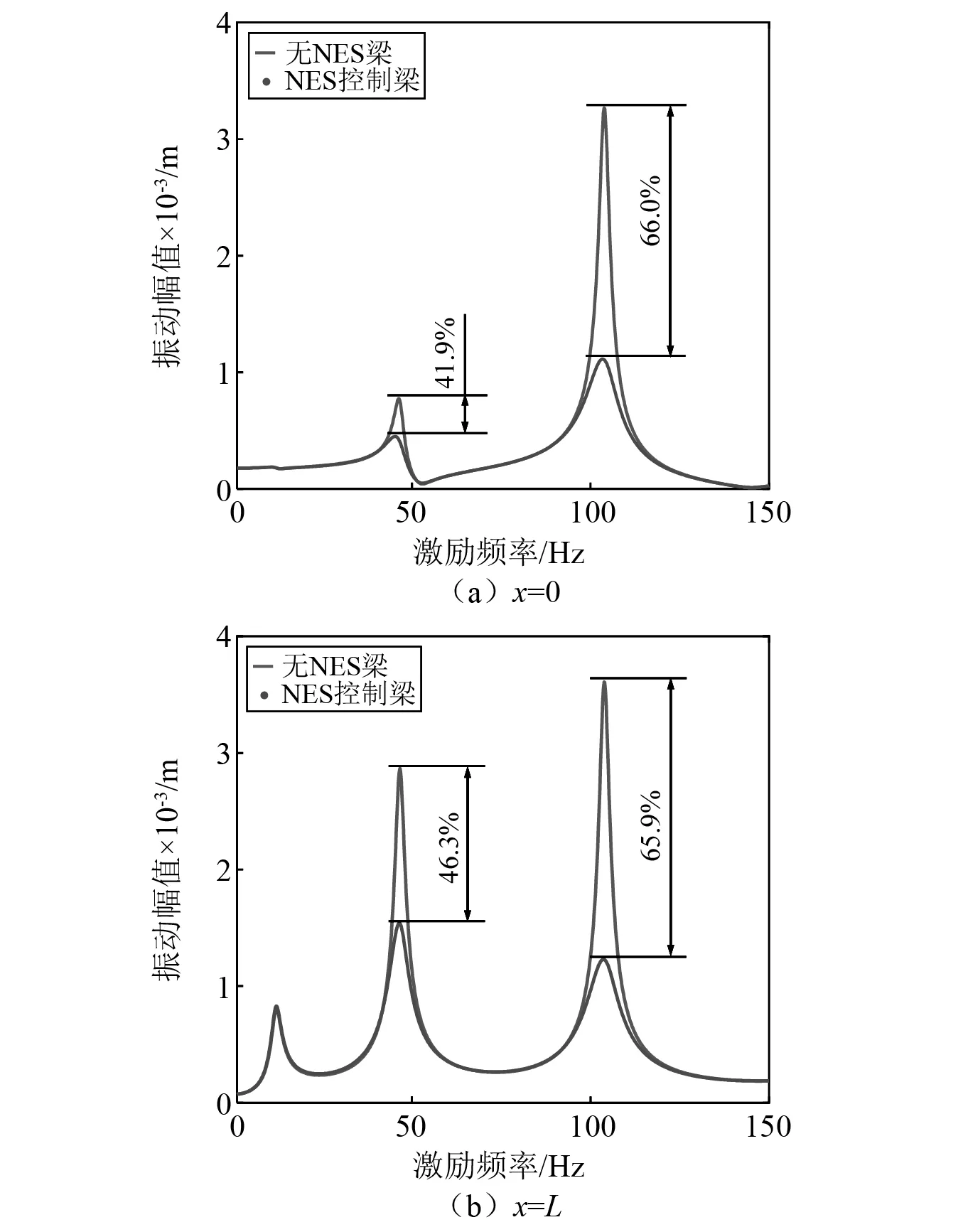
图4 knNES=1×109 N/m3时梁结构两端稳态响应的减振效果Fig.4 Vibration suppression effect for the stable responses at both ends of beam structure with knNES=1×109 N/m3

图5研究了当knNES=1×1010N/m时，非线性能量阱对梁结构端点处稳态响应的减振效果。其他参数与本节前述部分一致。由图5可知，此时非线性能量阱对梁结构振动系统端点处的吸振效果较knNES=1×109N/m时增强，但在第2阶主共振区处出现复杂动力学行为。上述现象说明非线性能量阱对梁结构端点处的振动状态影响显著。为深刻揭示非线性能量阱对梁结构动力学响应的影响规律，提高梁结构的减振效果，研究其非线性刚度、阻尼以及位置对梁结构动力学响应的影响规律就显得尤为重要。此外，根据工程经验，外部激励位置亦对梁结构的动力学响应具有显著影响。因此，在本节后续研究中，研究非线性能量阱的非线性刚度、阻尼、位置以及外部激励位置对梁结构动力学响应的影响规律。

图5 knNES=1×1010 N/m3时梁结构两端稳态响应的减振效果Fig.5 Vibration suppression effect for the stable responses at both ends of beam structure with knNES=1×1010 N/m3

图6研究非线性刚度对系统端点处动力学响应的影响。非线性刚度由1×108N/m3变化至1×1012N/m3。外部简谐激励频率为48 Hz。其他参数与本节前述部分相同。由图6可知，幅值-非线性刚度响应曲线存在两个不稳定区，在不稳定区内系统呈现复杂的动力学行为。在一定范围内增加非线性能量阱的非线性刚度对系统的减振具有有益的影响。

图6 梁结构两端幅值-非线性刚度响应曲线Fig.6 Amplitude-nonlinear-stiffness response curves at both ends of beam structure

图7分析了非线性能量阱阻尼变化对系统端点处动力学响应的影响。非线性能量阱的刚度取为1.5×1010N/m3。非线性能量阱阻尼由9 Ns/m变化至25 Ns/m。外部简谐激励频率为48 Hz。其他参数与本节前述部分相同。由图7可知，当非线性能量阱阻尼较小时，幅值-阻尼响应曲线存在一个不稳定区，在不稳定区内梁结构呈现复杂的动力学行为。增加非线性能量阱的阻尼能够抑制梁结构的复杂动力学行为且对端点处减振具有有益的效果。

图7 梁结构两端幅值-阻尼响应曲线Fig.7 Amplitude-damping response curves at both ends of beam structure

图8研究非线性能量阱位置变化对梁结构端点处动力学响应的影响。非线性能量阱的非线性刚度取为1×1010N/m3。非线性能量阱位置由0.1 m变化至0.9 m。外部简谐激励频率为48 Hz。其他参数与本节前述部分相同。由图8可知，当非线性能量阱靠近较硬侧边界时，幅值-NES位置响应曲线呈现稳态单周期状态。当非线性能量阱靠近较软侧边界时，幅值-NES位置响应曲线出现一个不稳定区。在不稳定区内梁结构呈现复杂的动力学行为。合理的布置非线性能量阱的位置能够避免梁结构出现复杂的动力学行为且对端点处的减振具有有益的效果。

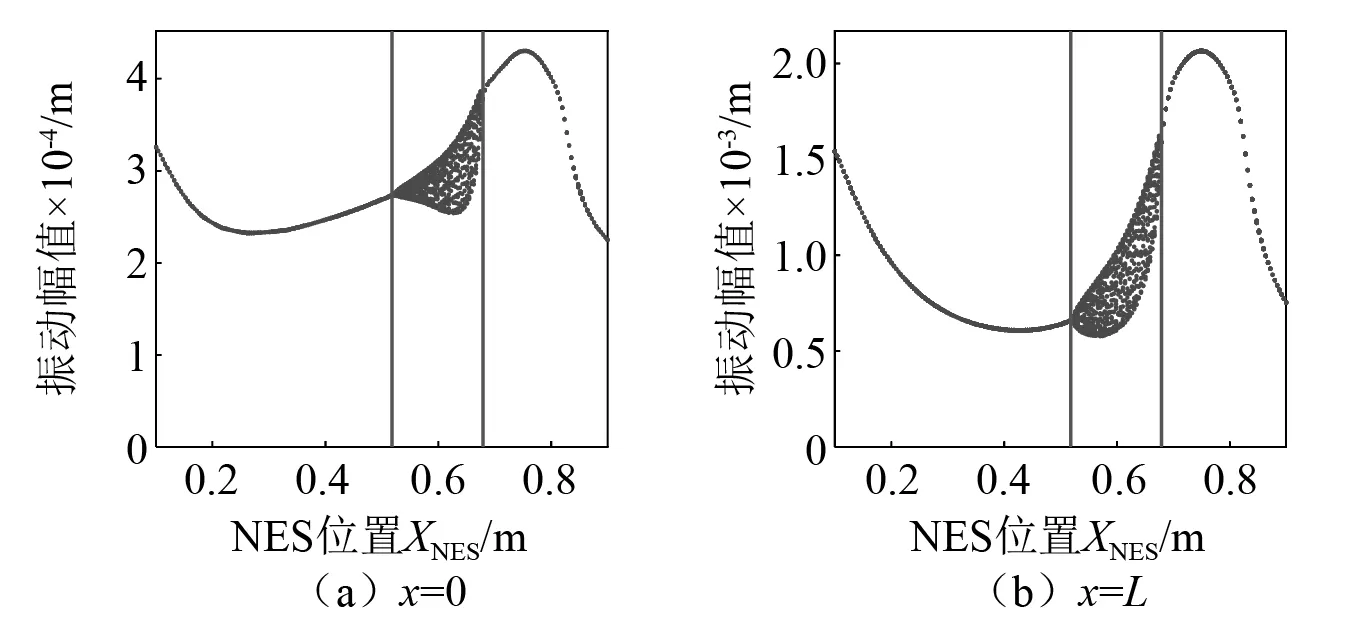
图8 梁结构两端幅值-NES位置响应曲线Fig.8 Amplitude-NES-position response curves at both ends of beam structure

图9研究激励位置变化对梁结构振动系统端点处动力学响应的影响。非线性能量阱的非线性刚度取为1×1010N/m3。外部简谐激励位置由0变化至1 m，外部简谐激励频率为48 Hz。其他参数与本节前述部分相同。由图9可知，幅值-激励位置响应曲线存在3个不稳定区，在不稳定区内梁结构呈现复杂的动力学行为。合理的布置外部激励位置能够有效抑制梁结构的复杂动力学行为且对其端点处的减振具有有益的效果。

综上所述，合适的非线性能量阱参数能够有效抑制梁结构端点处第2阶、第3阶主共振区的振动。在一定条件下，非线性能量阱的非线性刚度、阻尼、位置以及外部激励位置均能够显著改变梁结构的动力学响应特性。

3.3 非线性能量阱对梁结构端点处减振率的影响

在工程中，梁结构受到的外部简谐激励通常由动力设备引入。当动力设备、梁结构安装完成后其位置难以变更。梁结构所受的外部简谐激励位置亦难以变化。特别的，在船舶工程中，船舶轴系往往被简化为轴向载荷梁结构进行振动特性分析，其所受的外部简谐激励通常作用于轴系结构端部。此外，非线性能量阱的布置通常取决于结构的剩余空间且非线性能量阱的质量调节范围有限。综合考虑工程实践，本节研究非线性能量阱的非线性刚度、阻尼对梁结构减振率的影响。在本节计算中，梁结构参数、外部激励幅值、外部激励位置以及非线性能量阱质量、位置参数与3.2节中相同。外部激励频率选取为12 Hz，46.4 Hz，103.8 Hz，分别对应于线性系统的前3阶固有频率。定义梁结构左、右端点处的减振率为

(29)

(30)

式中，uW(·)为无非线性能量阱时具有弹性边界约束的轴向载荷梁结构振动系统的横向振动位移。

图10研究当外部激励频率为12 Hz时非线性能量阱非线性刚度、阻尼对梁结构端点处减振率的影响。非线性能量阱非线性刚度由1×107N/m3变化至1×1010N/m3。非线性能量阱阻尼由10 Ns/m变化至200 Ns/m。由图10可知，12 Hz下梁结构端点处的减振率随着非线性能量阱的非线性刚度、阻尼的变化在小范围内波动。非线性刚度、阻尼的变化对梁结构振动系统较软侧边界处的减振率微弱。对于外部激励为12 Hz的情况，改变非线性能量阱的非线性刚度与阻尼对梁结构端点处减振率的提升效果有限。

图10 12 Hz下NES非线性刚度、阻尼对梁结构端点处减振率的影响Fig.10 Influence of the NES nonlinear stiffness and damping on the vibration suppression rate at both ends of beam structure under 12 Hz

图11研究外部激励频率为46.4 Hz时非线性能量阱非线性刚度、阻尼对梁结构端点处减振率的影响。由图11可知，46.4 Hz下梁结构端点处非线性能量阱非线性刚度、阻尼的增加能够提高梁结构振动系统端点处的减振率。非线性能量阱的非线性刚度对梁结构端点处减振率的影响存在刚度敏感区。在刚度敏感区内增加非线性刚度能够显著增加梁结构端点处的减振率。对于本节所研究的梁结构参数而言，其非线性刚度敏感区为1×109N/m3至1×1010N/m3。非线性能量阱的阻尼对梁结构端点处减振率的影响存在临界值。当阻尼超过临界值时，梁结构端点处的减振率显著提高。

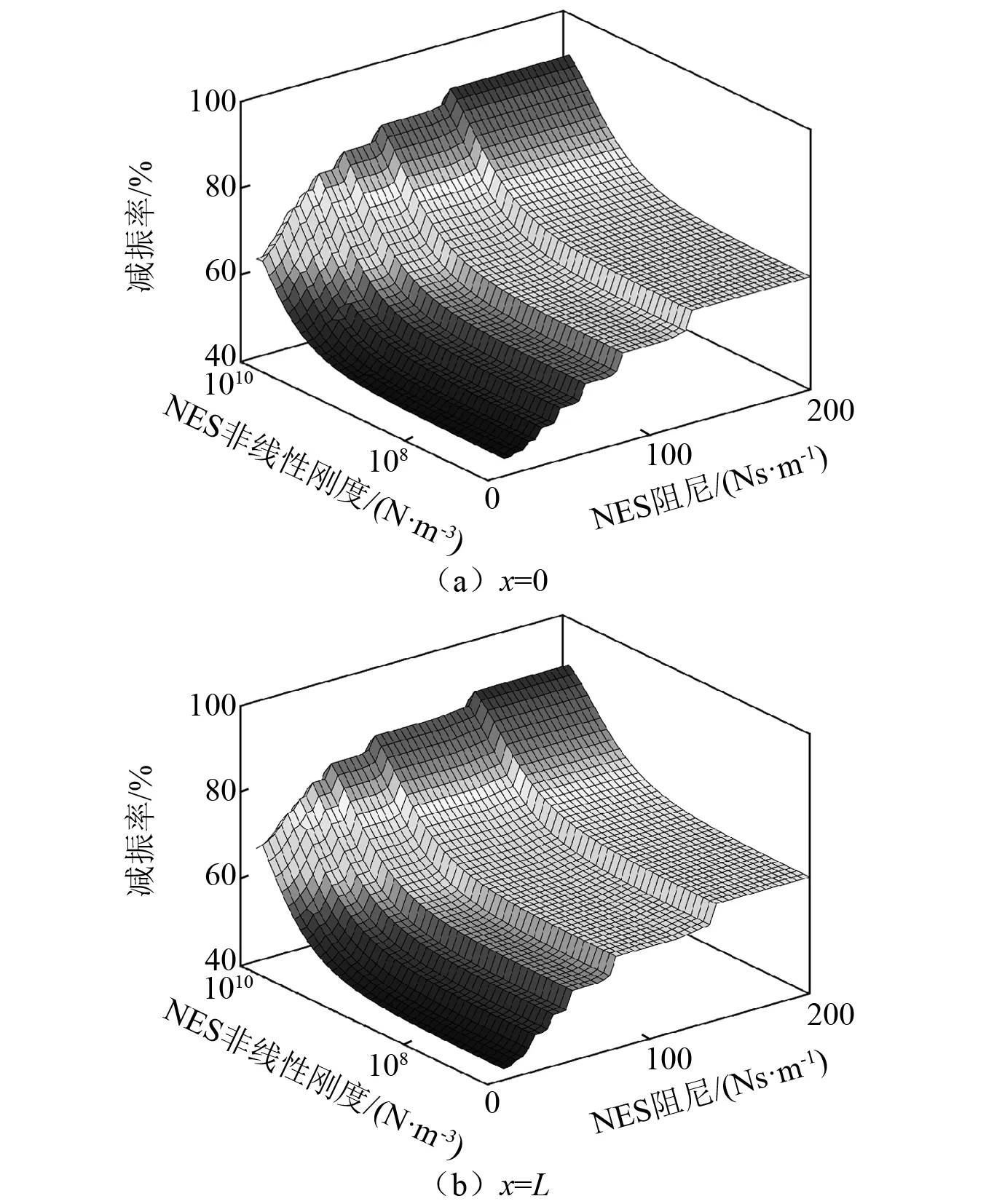
图11 46.4 Hz下NES非线性刚度、阻尼对梁结构端点处减振率的影响Fig.11 Influence of the NES nonlinear stiffness and damping on the vibration suppression rate at both ends of beam structure under 46.4 Hz

图12研究外部激励频率为103.8 Hz时非线性能量阱的非线性刚度、阻尼对梁结构端点处减振率的影响。由图12可知，103.8 Hz下梁结构端点处非线性能量阱非线性刚度、阻尼的增加能够显著提高梁结构振动系统端点处的减振率，其最佳减振效果能达到90%以上。与图11的分析类似，非线性能量阱的非线性刚度对梁结构端点处减振率的影响存在敏感区。在刚度敏感区内增加非线性刚度能够显著增加梁结构端点处的减振率。非线性能量阱的阻尼对梁结构端点处减振率的影响存在临界值。当阻尼超过临界值时，梁结构端点处的减振率显著提高。值得一提的是，103.8 Hz外激励频率下的非线性刚度敏感区、阻尼临界值与46.4 Hz外激励频率下的非线性刚度敏感区、阻尼临界值重合。

图12 103.8 Hz下NES非线性刚度、阻尼对梁结构端点处减振率的影响Fig.12 Influence of the NES nonlinear stiffness and damping on the vibration suppression rate at both ends of beam structure under 103.8 Hz

综上所述，当激励频率为线性系统第1阶固有频率时，非线性能量阱非线性刚度、阻尼对梁结构端点处隔振率的影响微弱。当激励频率为线性系统第2、第3阶固有频率时，非线性能量阱非线性刚度、阻尼对梁结构端点处隔振率的影响显著。在其他条件一定时，合适的非线性刚度与阻尼的组合能够显著提高梁结构振动系统端点处的减振率。在工程中，对于轴向载荷梁结构，在进行非线性能量阱的非线性刚度、阻尼进行优化时，首先应确定被控对象受到的外部激励频率。之后，研究非线性能量阱非线性刚度的刚度敏感区与阻尼临界值。在上述基础上，选取与被控对象振动特性匹配的非线性刚度与阻尼参数，实现轴向载荷梁结构的振动控制。

4 结 论

本文建立了具有非线性能量阱的弹性边界约束轴向载荷梁结构动力学预报分析模型。利用Galerkin截断法求解梁结构动力学响应，并与谐波平衡法所得结果进行对比，验证了本文方法的正确性，探讨了Galerkin截断数对结果稳定性的影响。在此基础上，研究了非线性能量阱参数与激励位置对梁结构动力学响应、减振效果的影响规律。主要结论如下：

(1)基于Galerkin截断法所构建模型能够准确预报具有非线性能量阱的弹性边界约束轴向载荷梁结构动力学响应，当截断数为4时梁结构动力学响应趋于收敛。

(2)非线性能量阱的引入能够有效抑制梁结构两端频率响应曲线第2、第3阶主共振区内的振动。

(3)非线性能量阱参数及激励位置对梁结构振动状态影响显著。非线性能量阱非线性刚度在一定范围内使得梁结构端点处呈现复杂动力学行为；非线性能量阱阻尼增加能够有效抑制梁结构的复杂动力学行为，并对梁结构减振具有有益作用；合理的布置非线性能量阱的位置以及外部激励位置能够避免梁结构出现复杂的动力学行为且对梁结构端点处的减振具有有益的效果。

(4)当激励频率为线性系统第2阶、第3阶固有频率时，非线性能量阱刚度、阻尼参数的增加可以改善梁结构端点处的减振率；合适的非线性刚度、阻尼参数能够显著提高梁结构端点处的减振率。