岷江梯级水库群航运-发电多目标协调调度研究
2023-01-03杨悦,张绪进,马光文,陈仕军,黄炜斌
杨 悦,张 绪 进,马 光 文,陈 仕 军,黄 炜 斌
(1.四川大学 水利水电学院,四川 成都 610065; 2.重庆交通大学 西南水运工程科学研究所,重庆 400074)
0 引 言
根据中共中央、国务院在《交通强国建设纲要》[1]中有关交通强国建设战略部署,为推动内河航运高质量发展,2020年5月29日交通运输部印发了《内河航运发展纲要》[2],指出内河航运对促进流域经济发展的重要作用,明确要强化东西水运大通道,提升中西部地区主要支流航道,形成长江干线横向通道。航运能力的拓展对长江经济带、西部大开发新格局、“一带一路”、成渝地区双城经济圈等重大国家发展战略实施具有深远的影响。面对经济社会的快速发展,船舶大型化、标准化趋势明显,船舶载重量增加,吃水随之增大,现有的大部分库区航道等级已不能满足航运需求。目前提升航道等级、挖掘航运能力的途径可分为工程措施和非工程措施。但在长江“共抓大保护、不搞大开发”“生态优先、绿色发展”的大背景下,传统的航道整治工程措施受到环境保护的制约不可能大规模实施。因此,通过梯级水库群联合调度等非工程措施,增加河道通航流量、改善河道通航条件显得十分迫切和重要[3]。
目前,制约中长期航道等级提升的关键问题在于枯季流量小、水位低,从而造成许多大型船舶因河道航深不能满足而无法通行,只能集中在汛期运输,造成货物积压,不利于经济发展。但是要满足枯季的航运补水需求意味着需要调整水库消落方式,可能会对水电站发电量造成影响,进而影响发电企业的收益。为协调航运与发电二者之间的矛盾,相关学者进行了研究。刘俊萍等[4]以梯级水电站群多年平均发电量最大为优化目标,详细分析了考虑和不考虑航运需求下的优化结果,讨论了发电和航运效益之间的相互影响关系。赵云发等[5]以三峡水电站为研究对象,分析计算其航运和发电效益,结果表明枯季流量补偿能够增加三峡水电站航电的综合效益;张继顺等[6]对三峡水库蓄水发电后的枯季航运流量补偿效益进行分析,提出三峡水库的枯期库容使用规则;王学敏[7]以累计滞留载货作为航运的评价标准,建立了汛期航运-防洪多目标优化模型和蓄水期航运-生态-发电多目标优化模型;周建中等[8]将航运效益通过下泄流量与通航保证率间的映射关系来量化,建立了汛期水库多目标优化调度的模型,提升了汛期通航保证率和发电量;黄馗[9]通过对比分析广西主要水电航运枢纽在枯期和汛期的运行规律,提出基于保证通航效率的汛末水库蓄满率建议;张先平等[10]以三峡-葛洲坝梯级水库群为例,通过拟定不同的航运控泄流量、控制水位指标和调峰幅度等,对兼顾航运需求的水库群调度方案进行研究,并提出应开展长江上游梯级水库联合调度对枯期补水能力的研究;吴文凤等[11]利用岷江上游水库总调节库容,计算联合调度理论上可以增加的枯期流量,结合平面二维水流模型给出了要满足航道标准所需要的最小通航流量;田锐[12]研究了以总发电量最大、生态溢缺水量最小和通航破坏深度最小的流域水库群多目标优化调度模型,以提升水库群综合兴利效益。上述研究大多以累计滞留载货或下泄流量变幅最小、通航破坏深度最小等指标作为航运目标,鲜有考虑流域下游航道冬春枯期航运补水需求、提高枢纽枯期下泄流量的研究,且针对流域大规模梯级水库群的航运与发电协调调度研究较少。
为充分发挥长江上游大型水库群调节库容的作用,提升长江上游主要支流航道的通航能力,本文研究了一种兼顾航运需求和发电效益的梯级水库群多目标协调调度模型及其高效求解的PSO-POA改进算法,并以岷江流域梯级水库群为例进行仿真模拟分析,进一步验证本文所构建模型及其求解算法的合理性和可行性。研究成果对指导流域通过梯级水库群多目标协调调度来改善航道通航条件,缓解因航运和发电对水库蓄放水需求不一致造成的矛盾具有重要意义。
1 梯级水库群航运-发电多目标协调调度模型
结合河道冬春枯期航运补水的需求,为协调梯级水库群中长期调度中枯期发电效益与航运需求之间的矛盾,本文以提高下游河道枯期通航流量为航运目标、以总发电量最大化为发电目标建立梯级水库群航运-发电多目标协调调度模型,充分利用大型水库的调节库容和梯级水库群联合调度空间实现综合利用效益最大化。
1.1 目标函数
(1)航运目标。为了尽可能提高下游河道的通航流量,以控制断面最小通航流量尽可能大,即年内最小通航流量最大化为目标,目标函数可以写成:
maxf1=maxQ*=maxmin{Q末,1,Q末,2,…,Q末,T}
(1)
式中:Q*为控制断面最小通航流量最大化的计算指标,m3/s;Q末,t为梯级最末一级电站在第t时段的出库流量与该电站至控制断面第t时段的区间流量之和,m3/s;T为调度期总时段数。
(2)发电目标。为了充分利用梯级水库群水电能源资源,给电网提供尽可能多的清洁可再生的电量,以梯级水电站群年发电量最大化为目标,其函数表达式可以写成:
(2)
式中:E为梯级水电站群的全年总发电量,kW·h;Ki为第i个电站的出力系数;qi,t为第i个电站在第t时段的发电流量,m3/s;Hi,t为第i个电站在第t时段的平均发电毛水头与水头损失之差,m;Mt为第t时段的小时数,h;N为梯级水电站个数。
1.2 约束条件
(1)水量平衡约束。梯级水库群运行时应遵循水量平衡方程。
Vi,t+1=Vi,t+(Si,t-qi,t-Ii,t)Δt
(3)
式中:Vi,t+1为第i个电站在第t时段末的水库蓄水量,m3;Vi,t为第i个电站在第t时段初的水库蓄水量,m3;Si,t为第i个电站在第t时段的入库流量,m3/s;Ii,t为第i个电站第t时段的弃水流量,m3/s。
(2)水库水位约束。为保证梯级水库群正常运行,水电站的汛期运行水位应在汛限水位和死水位之间,平水期和枯水期的运行水位应在正常蓄水位和死水位之间。
(4)
式中:Zi,t为第i个电站在第t时段初的水库水位,m;Zi,t下、Zi,t上为第i个电站在第t时段初的水位下、上限,m。
(3)水库下泄流量约束。为保障水电站自身安全、机组安全和梯级水库综合利用需求,水电站下泄流量要满足最小下泄流量和最大下泄流量的要求。
(5)
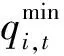
(4)电站出力约束。水电站出力应在允许的上限和下限范围内。
(6)
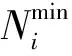
(5)水量联系约束。梯级水电站上下游间的流量传递,应满足上下游流量平衡。
Si,t=qi-1,t-1+Ii-1,t-1+Oi,t
(7)
式中:qi-1,t-1为第i-1个电站(第i个电站的上游电站)在t-1时刻(前一时刻)的发电流量,m3/s;Ii-1,t-1为第i-1个电站(第i个电站的上游电站)在t-1时刻(前一时刻)的弃水流量,m3/s;Oi,t为第t时刻第i-1个电站到第i个电站的平均区间入流,m3/s。
(6)非负条件约束。以上所述所有变量均应为非负变量(≥0)。
2 模型求解算法
目前水库群协调调度领域广泛应用的算法主要分为数学规划方法和智能算法两类。前者经过较长的发展和应用实践,算法较为成熟,但在处理大规模问题时易陷入维数灾[13-15]。后者解决非凸、非线性的大规模复杂优化问题具有计算速度快、算法原理简单、程序易实现等优势,是目前研究的热点,但由于随机性较强而难以找到稳定的可行解,算法的应用还处在探索阶段[16-19]。因此,使用单个算法存在局限性,目前许多学者研究多种算法嵌套的方法,以获得较好的求解算法[20-21]。数学规划方法中的POA算法收敛性好且能有效减少规划方法的高数维[22],在协调调度中应用广泛。该算法实质上是以某个初始轨迹的一端为起点进行的渐进优化求解算法,因此其初始轨迹和步长的选取显得十分重要,不但影响求解速度和精度,还决定着会不会陷入局部最优、能否找到全局最优解。为此,本文对POA算法进行改进,采用粒子群算法(PSO)的飞行策略得到较优的初始解集,并通过变步长方法平衡全局和局部搜索能力。本文将PSO-POA改进算法应用于梯级水库群航运-发电效益多目标协调调度模型的求解计算,图1为PSO-POA改进算法的基本计算流程图。该算法的具体求解流程如下:
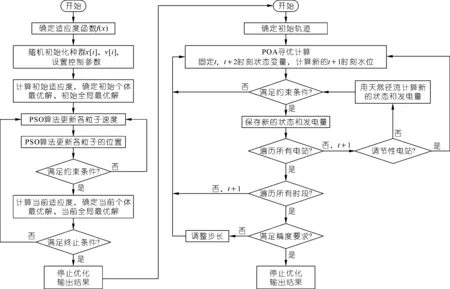
图1 PSO-POA改进算法计算流程
(1)确定PSO算法的飞行策略,即粒子速度和位置状态的更新公式:
(8)
(9)

(2)确定适应度函数,随机初始化种群,并设置基本参数。本文所建模型为多目标问题,为求解便利,将目标函数式(1)转化为约束,并加入目标函数式(2)中作为惩罚项,转化后模型的目标函数,即适应度函数为
(10)
式中:A为惩罚因子,ε为假定的年内最小通航流量最大化后的最小值。根据控制断面的年内最小通航流量计算结果动态调整,φt定义为
(11)

(4)依据公式(8)~(9)对粒子位置和速度进行更新,并计算更新后的适应度值,与历史个体极值和全局极值进行比较,确定当前个体最优位置和当前全局最优位置。
(5)再重复步骤(4),直到达到最大迭代次数,输出得到的结果作为POA算法较优的初始轨迹。
(6)确定逐步优化算法的参数,依照梯级电站的顺序,首先固定第一级电站的第0时刻和第2时刻的水位不变,然后调整第1时刻的水位(分别取在原水位的基础上减少1步长、不变和增加1步长3种情况),计算各方案的第0到1时刻和第1到2时刻这两个两阶段的目标函数,比较分析后选择目标函数最优的方案作为该电站第1时段的新水位,并更新水位轨迹。同样的方法,逐次推后一个时段,固定两端,对中间时刻的水位进行调整,直到遍历所有电站和所有时段,完成一次循环。将本次循环计算的各时段末的新水位,作为下一次寻优计算的新的初始轨迹。
(7)重复步骤(6),随着目标值的变化范围缩小(逐渐收敛),相应的减小步长,直到新值与历史最大值的绝对差值在要求精度内,即|E-maxE|≤0.1亿kW·h,输出本次计算得到的梯级水库群最优运行方案。
3 实例研究
四川省素有“千河之省”之称,拥有长江、岷江、嘉陵江、渠江等水运通道,因其丰富的运能资源以及地处西部内陆和长江上游的特殊地理位置,在国家的航道布局中具有重要地位。其中岷江航道是国家高等级航道之一,对运输川西、川南物资运输和促进区域对外交流具有十分重要的作用[23]。随着社会经济的发展,岷江航道已难以满足货物运输的规划要求,需大力提升其水运能力[24]。根据《长江干线航道总体规划纲要》,岷江下游乐山至宜宾160 km段航道将提高至Ⅲ级航道标准,中游彭山至乐山115 km段航道提高至Ⅳ级航道标准。但因该区域涉及长江上游珍稀特有鱼类保护区,工程整治措施受限,且岷江流域河川径流主要为降雨补给,年内分配不均,枯期流量很小,往往难以满足航运需求。而随着岷江流域上游梯级水库群逐渐形成,为通过梯级水库群联合优化调度增大下游枯水期流量,提高航道水深,提升枯水期航道运输能力创造了有利条件。因此,本文以岷江流域为研究对象,利用上游大金水文站的实测径流资料选出丰、平、枯典型年(2017,1998,1977年),开展梯级水库群航运-发电多目标协调调度实例研究,验证所建模型的合理性和所提算法的可行性。
3.1 基本资料与参数设置
本文以岷江流域上游双江口水库至下游犍为水电站的“4库16级”梯级水库群为实例进行研究,各个水电站的正常蓄水位、死水位、装机容量、出力系数等特征参数如表1所列。
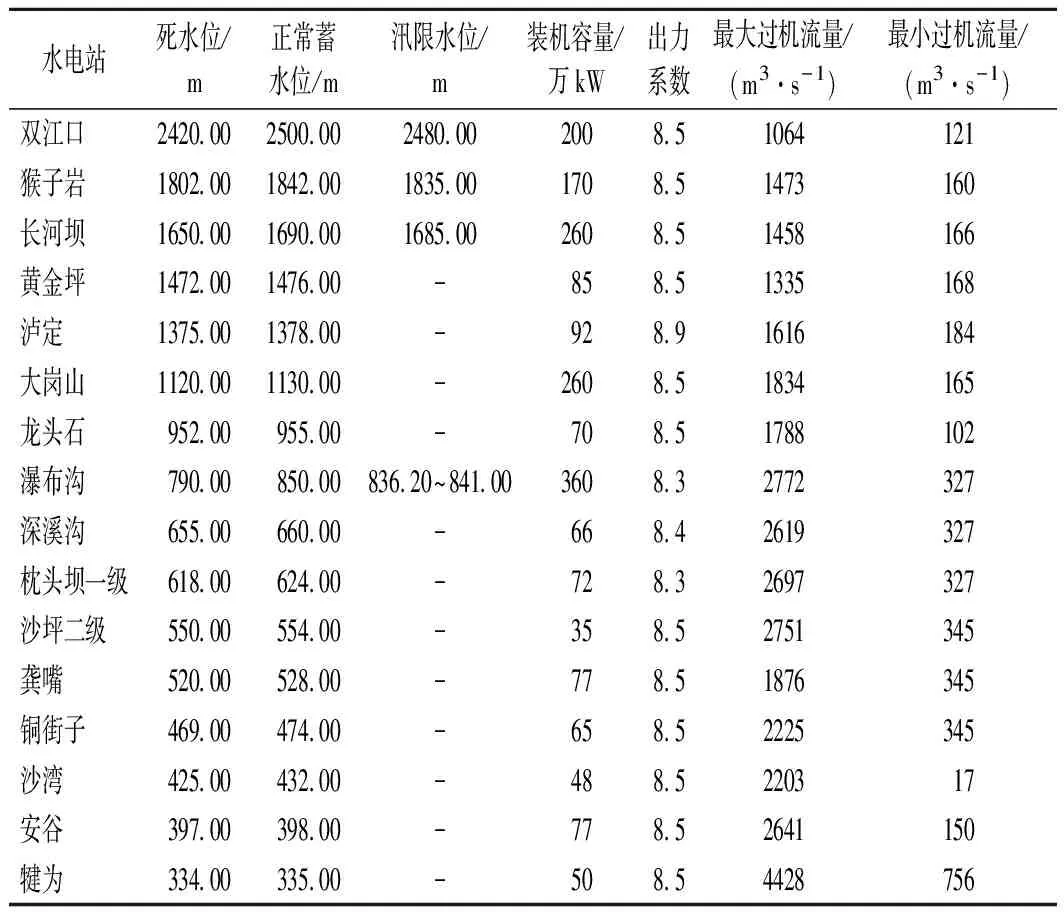
表1 岷江梯级水电站特征参数
其中,双江口、猴子岩、长河坝和瀑布沟4座水库具有季及以上调节能力,其他水电站仅具有日及以下调节能力,在梯级水库群中长期协调优化调度时仅考虑其作为径流电站参与联合调度的发电效益。本文以岷江下游高场站断面的通航流量为模型中航运目标的控制对象,利用岷江流域丰、平、枯3个典型年的实测径流资料进行实例计算。经软件测试,得到PSO-POA算法的最优参数如表2所列。
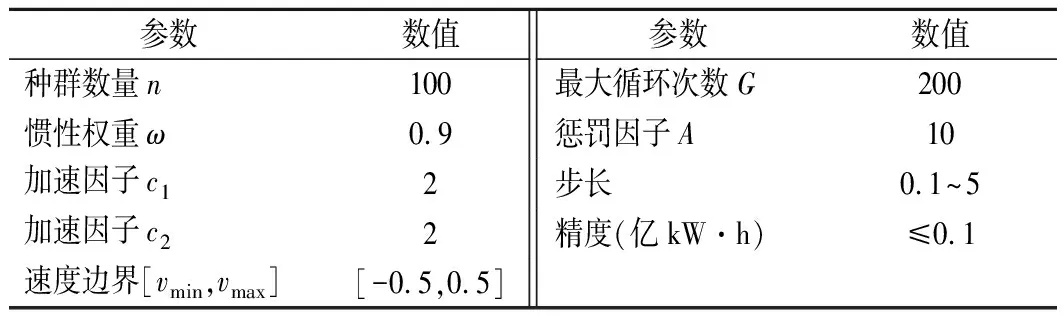
表2 PSO-POA算法参数设置
3.2 优化结果及分析
结合岷江流域梯级水库群的实际资料,运用PSO-POA改进算法对丰、平、枯典型年梯级水库群航运-发电多目标协调调度进行实例计算。同时为便于开展航运目标和发电目标的结果分析,将传统的仅以梯级发电量最大化目标的梯级联合优化调度模型(以下称“模型2”)进行计算,并与本文所建立的航运-发电多目标协调调度模型(以下称“模型1”)进行对比分析。图2给出了模型1在丰、平、枯典型年下非劣前沿计算结果和模型2的计算结果。
由图2可知,年内最小通航流量最大化与梯级总发电量两个目标的非劣解集的分布趋势呈反比,当岷江下游高场站断面的通航流量增加时,梯级电站群总发电量随之降低,证明该河段航运效益与发电效益存在相互制约的关系。由非劣前沿呈凸函数形式可以看出,当最小通航流量增加到一定值时,发电量会显著下降,而通航流量的增加不大。分析原因是由于最小通航流量在增加初期,不满足需求的旬数较少,因此需要调整的流量少,梯级水库可以通过互补调节同时满足发电效益和航运效益,但在提高到一定值后,不满足需求的旬数增多,流量需求随之增加,若继续提高通航流量,会引起发电量显著下降。因此选取该点作为航运-发电多目标协调调度模型(模型1)的均衡方案,与梯级发电量最大化目标的梯级联合优化调度模型(模型2)进行比较,两个模型计算结果中通航流量与原天然径流三者的对比见图3,两个模型的发电量结果对比见图4,各目标值对比见表3。
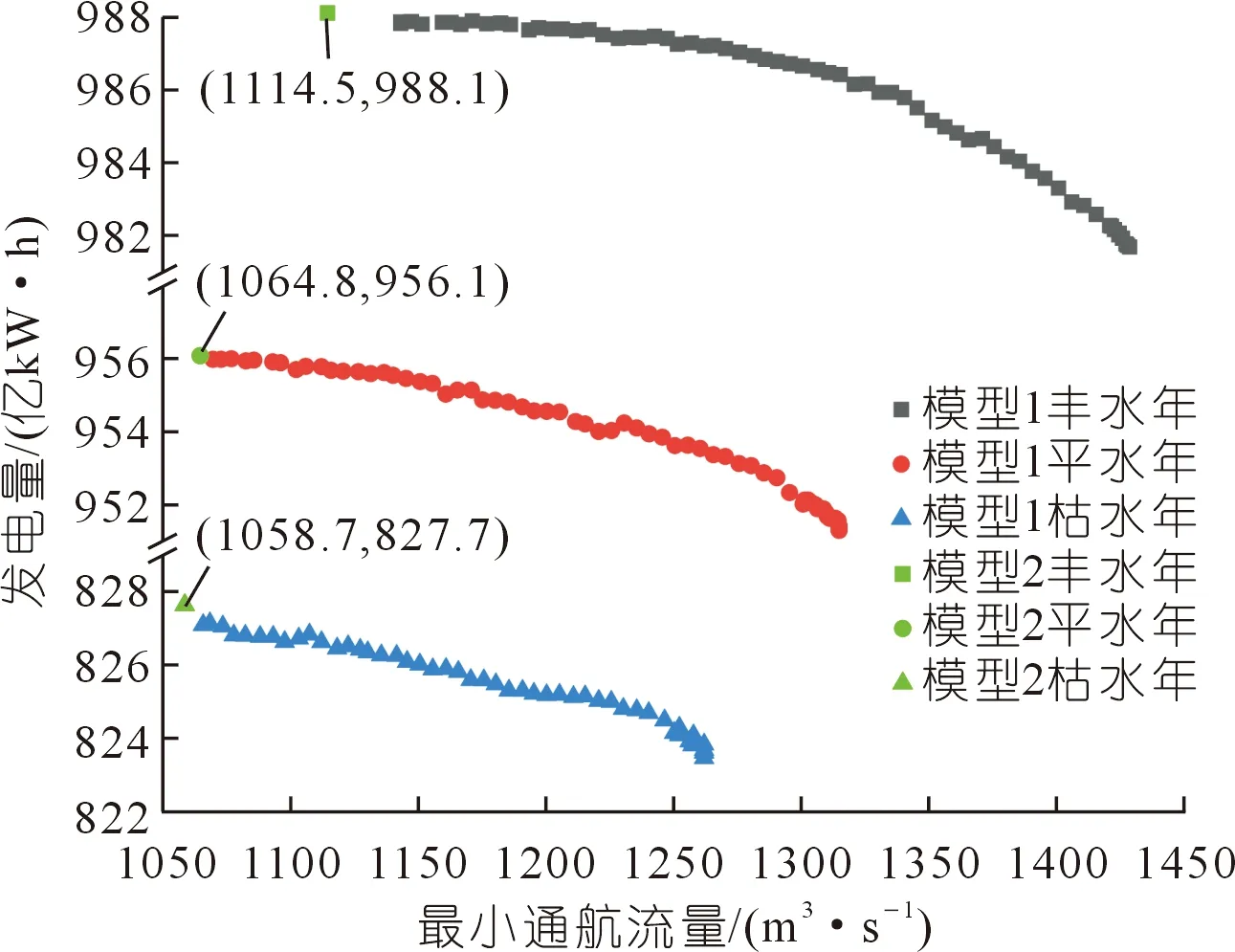
图2 不同典型年下模型1与模型2非劣前沿计算结果

图3 高场断面通航流量过程对比
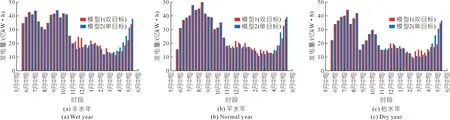
图4 梯级水电站群年总发电量对比
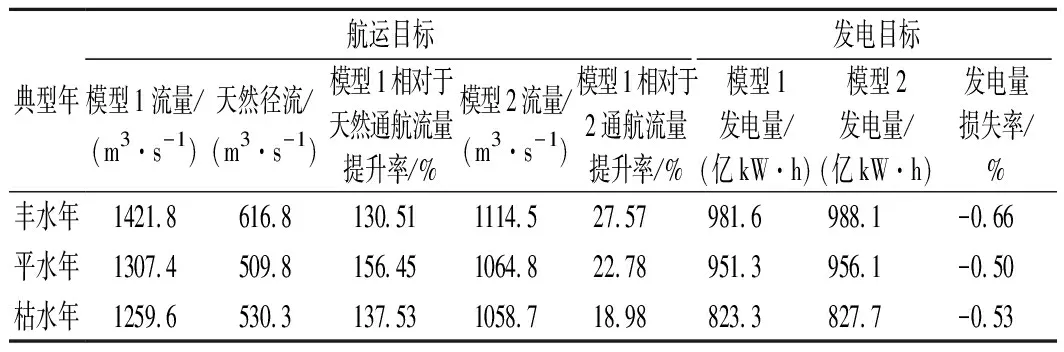
表3 丰平枯典型年下各目标值对比
由图3和表3可知,与天然径流相比,模型1显著提高了枯期12月至次年4月的河道通航流量,将丰平枯典型年下年内最小旬天然径流616.8,509.8 m3/s和530.3 m3/s分别提高至1 421.8,1 307.4 m3/s和1 259.6 m3/s,年内最大提升率分别为130.51%,156.45%,137.53%。可见在不同典型年下,当枯期天然来水流量很小、航运补水需求强烈时,模型1对枯期下游河道的流量提升效果十分突出,可有效缓解枯期河道航运压力。与模型2相比,模型1对枯期的河道通航流量也有明显提升,年内最大提升率分别为27.57%,22.78%,18.98%,这是因为模型2为了增加发电量,需要尽可能保持水库高水头运行,在汛末尽可能不消落水位,将水库蓄水量集中于枯水期末消落放水,而枯期前几个月通航流量偏小,不利于保障航运用水需求。总之,在模型1下,梯级水库群的枯期出库流量得到均化,使得航道的水流条件相对平稳,将水库的蓄水量相对均匀他用于补给枯水期河道流量,增加航道通航水深,更有利于船舶通行。
由图4和表3可知,与模型2相比,模型1对发电量的影响主要在枯期,这是因为模型1下梯级水电在枯期降低水头增加下泄流量以提高枯期通航流量,牺牲了部分发电效益,其中模型2仅以发电量最大化为目标,丰平枯典型年下年总发电量分别为988.1亿,956.1亿kW·h和827.7亿kW·h,模型1同时以发电量最大化和控制断面年内最小通航流量最大为目标,丰平枯典型年下年总发电量分别为981.6亿,951.3亿kW·h和823.3亿kW·h,发电量损失率分别仅为0.66%,0.50%和0.53%。
从整体来看,模型1能够以较小发电效益损失实现对梯级水库群下游枯期通航流量的较大提升,可以兼顾梯级水库群的发电效益和通航效益。可见航运效益与发电效益并不是完全冲突的关系,从通航流量提高的内在机理分析原因是由于发电效益主要受发电流量和水头影响。传统调度方式下枯期初期尽可能维持高水位,以水头效益增加发电量,在枯期末期快速消落水位,以流量效应增加枯期末期的发电量。在航运-发电多目标协调调度方式下,经过梯级水库补偿调节,枯期增加下泄流量以满足通航需求,虽然较传统调度方式降低了运行水头,但是用于满足通航需求的这部分下泄流量也用于发电,增加了流量效益,使得发电效益只有小幅度减少。
为剖析在兼顾发电效益和通航效益目标下梯级水库群和大中型水库在丰、平、枯典型年的运行调度方式,将模型1与模型2中双江口、猴子岩、长河坝、瀑布沟水库的水位过程进行对比分析,如图5所示。
由图5可知,模型1和模型2中各水库电站水位变化的不同主要在枯期,即不同目标下汛末水库消落水位控制方式不同。从整体来看,在丰、平、枯典型年梯级各水库的水位变化趋势整体较为接近,模型2中各水库在枯期尽可能保持高水位运行以获得较高的水头效应,增加梯级总发电量;而模型1下各水库提前消落水位,以增加下游电站的枯期出库流量,使下游河道在枯期12月至次年4月均能有较大且稳定的通航流量。

图5 梯级各水库水位过程对比
通过横向对比发现,在3个典型年下双江口水库总是最先开始消落,这是因为按照梯级水库的流量和水头传递规律,在相同的出库流量下,相比于先消落下游电站,优先消落上游电站水位可以提高下游电站的水头,使得梯级总水头增加,以增加梯级总发电效益。通过纵向对比发现随着枯期天然来水流量的逐渐减少,双江口水库在不同模型下的消落水位趋势逐渐接近,主要是由于作为流域的龙头调节性水库,其消落方式对梯级发电效益有较大影响,当来水流量级变小,所需要的梯级总调节库容变小,上游水库将以发电量最大为主要目标控制消落方式。对于猴子岩和长河坝水库,通过横向和纵向对比发现,在不同模型下两个水库的水位消落方式均有较大差异,分析原因是由于猴子岩和长河坝水库受调节性能的限制,对在发电量最大化目标基础上增加的航运目标比较敏感,面对枯期较大的补水需求通过提前消落水头来实现。对于瀑布沟水库,通过横向和纵向对比发现,在不同典型年下大致都是从12月枯期开始一直消落到次年4月枯期结束,在整个枯期起到比较好的调节和补水作用。因此兼顾航运与发电效益的梯级水库群调度要依据流域梯级水库电站的上下游关系、调节性能差异等特点科学消落水位,重点利用好靠近补水需求断面的大型水库的调节库容,可以有效改善河道通航条件,缓解枯期航运需求与发电效益的矛盾。整体来看,各水库水位消落的起始时间和消落期长度符合梯级间水量传递关系,反映了水库的调节性,进一步验证了调度方案的合理性和科学性。
为对比文中所提PSO-POA改进算法的合理性和时效性,分别采用PSO算法和POA算法对平水年进行实例计算,其中PSO算法循环次数设置为2 000次,POA算法以水库水位均匀蓄满和消落作为初始水位,其余参数与PSO-POA改进算法中参数设置相同,优化结果如表4所列。可以看出在相近的计算时长下PSO算法因其随机性较强难以仅通过一次计算就找到多目标问题的非劣解。在相同的精度要求下,POA算法易陷入局部最优,且在没有合适的初始轨迹下寻优用时更久。由此可知PSO-POA改进算法能够综合PSO算法全局搜索能力强和POA算法鲁棒性好的优点,在求解精度和速度方面具有优势。
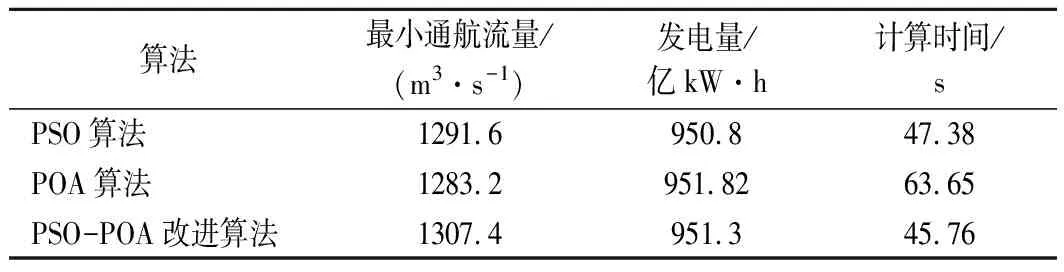
表4 不同计算方法下优化结果对比
4 结 论
本文基于航运对水库调度的补水需求,以充分发挥梯级水库群的发电与航运综合效益为出发点,建立了以最小通航流量最大化和总发电量最大化为目标的梯级水库群多目标协调调度模型;研究了适用于多目标协调调度模型求解的PSO-POA改进算法,克服传统POA算法初始轨迹选择困难和易陷入局部最优的问题,以及随机算法PSO优化结果不稳定的问题;最后,通过岷江梯级水库群丰、平、枯典型年的实例仿真进行计算。结果表明:在兼顾航运与发电效益的多目标梯级水库群联合调度下,不同代表年的岷江下游高场站断面的最小通航流量分别为1 421.8,1 307.4 m3/s和1 259.6 m3/s,梯级水电站群年发电量分别为981.6亿,951.3亿kW·h和823.3亿kW·h,与仅考虑梯级水电站年发电量最大的单目标模型的计算结果相比,实现了对丰、平、枯3个代表年最小通航流量的有效提升,提升率分别为27.57%,22.78%和18.98%,而梯级年发电量损失率分别仅为0.66%,0.50%和0.53%。
总而言之,本文所提模型和求解方法有效缓解了发电效益与航运效益的矛盾关系,在提高河道通航流量以满足航运需求的同时,又能较好地保证梯级水电站群的总发电量,得到的岷江梯级水库群联合调度方案可为实际调度和航道扩能提升方案决策提供参考。另外,本文所建模型可以求解流域通过梯级水电协调调度能够提高的最大通航流量,对未来各梯级水库调度时下泄通航流量的控制指标具有重要参考意义,能够为流域航道规划设计提供科学依据。所提模型和算法亦能应用在其他需要兼顾发电效益和通航效益的梯级水库群,具有较大的推广应用价值,研究工作对促进梯级水库群综合效益的发挥具有重要意义和工程应用价值。
