基于机器学习的爆破空气超压预测
2023-01-03陈资,梁福志
陈 资,梁 福 志
(广东理工学院 工业自动化系,广东 肇庆 526100)
0 引 言
爆破作为采矿和土木工程中广泛应用的岩石开挖方法,会不可避免地引发一系列安全和环境问题,例如地面振动、飞石、空气超压(air-overpressure,AOP)、粉尘等[1-2]。其中,空气超压会对工人以及爆破周边地区的建(构)筑物造成严重的危害,为此实现对AOP的精确预测显得愈发重要[3]。
目前国内外专家学者关于AOP预测的研究方法主要分为两类:① 基于萨道夫斯基公式建立的经验公式预测方法,但是它考虑的AOP影响因素少,并且无法准确建立AOP及其影响因素之间的不确定、复杂、非线性关系,所以其预测效果不佳[4];② 基于人工智能算法的预测模型。如张瑞华[5]分析了蒸气云爆炸超压的各种影响因素,利用BP神经网络预测蒸气云爆炸超压;Khandelwal等[6]基于支持向量机(Support Vector Machine,SVM)对AOP进行预测,并与传统的经验公式预测结果对比分析;Mohamad等[7]提出了遗传算法(genetic algorithm,GA)优化的人工神经网络(Artificial Neural Networks,ANN)预测模型;Harandizadeh等[8]结合概率神经网络(PNN)和自适应神经元网络方法(ANFIS),对AOP预测进行了研究。
相比于以上算法,基于结构风险最小化准则建立的最小二乘支持向量机(Least Squares Support Veotor Maohine,LSSVM)能有效解决AOP影响因素之间具有的非线性关系复杂、样本容量小等问题,并且运算效率和精度高于SVM[9]。合理设置LSSVM参数是决定LSSVM预测精度的关键,传统方法一般用梯度下降法或网格搜索法进行参数寻优,而灰狼算法(Grey Wolf Optimizer,GWO)作为一种模仿狼群狩猎行为的新型元启发式算法,具有全局搜索能力强、调用参数少、收敛速度快等优点,已被广泛应用于参数寻优问题[10]。
综上所述,本文首先使用灰色关联分析法(Grey Relational Analysis,GRA)筛选出影响AOP的关键因素,并作为LSSVM的输入变量,消除次要影响因素的干扰,随后通过引入灰狼算法优化LSSVM参数,最终提出了基于GRA-GWO-LSSVM的爆破AOP预测模型,并通过实例验证该模型的有效性与可靠性,以更好地控制爆破工程安全。
1 基础理论
1.1 灰色关联分析(GRA)
灰色关联理论能较有效地衡量研究对象和其相关因素行为序列之间的关联程度[11]。由于该方法对变量样本大小没有要求,并适用于不规律分布的数据,因此被广泛应用于寻找研究对象的关键因素[12-13]。其计算流程如下:
(1)确定母序列和子序列。将研究对象作为母序列X0={x0(1),x0(2),…,x0(n)},影响因素作为子序列,其中第i个相关子序列表示为Xi={xi(1),xi(2),…,xi(n)},i=1,2,…,m。
(2)数据归一化处理。为防止不同变量间量纲差异过大造成关联度计算结果误差偏大,需要对初始样本数据归一化处理。计算公式如下:
(1)
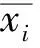
(3)灰色关联系数计算。x0(k)与xi(k)在第k点的关联系数ζi(k)为
(2)
式中:ρ为分辨系数,且ρ∈[0,1],通常选0.5。
(4)灰色关联度计算。子序列Xi对母序列X0的关联度ri计算公式为
(3)
关联度ri的取值范围为(0,1),一般认为若关联度ri≥0.8,则子序列与母序列具有良好的关系;若关联度0.5≤ri<0.8,则具有较好的关联度;若关联度ri<0.5,则子母序列基本不相关[14]。
1.2 LSSVM算法
LSSVM的基本思想是通过非线性转换,将输入向量映射到高维特征空间,转化为线性回归问题[15]。对于输入训练样本{xi,yi}(i=1,2,3,…,l),其线性回归函数为
f(x)=ω·φ(x)+b
(4)
式中:ω为权向量;φ(x)为非线性映射函数;b为偏置值。
根据结构风险最小化原则,将求解权向量ω和偏置值b的问题转化成最优化问题:
(5)
式中:ei为误差;γ为惩罚因子。
设拉格朗日乘子为ai,构造拉格朗日函数如下:
(6)
L分别对ω、b、ei和ai进行求偏导,则有:
(7)
求解式(7),可得非线性模型:
(8)
式中:K(x,xi)为核函数。由于RBF核函数具有形式简单、适用范围广、泛化能力强等优点,因此,本文选RBF核函数作为LSSVM中核函数。其表达式为
(9)
式中:σ为核函数参数。
1.3 GWO对LSSVM的参数优化
在传统LSSVM预测模型中,惩罚因子γ和核函数参数σ的选择对预测精度影响很大。GWO算法是一种新型的群体智能优化算法,主要思路是通过模拟自然界中灰狼种群的社会等级和群体狩猎行为来实现全局优化[16],具有全局搜索能力强、调用参数少的特点。因此本文引用该算法对LSSVM模型进行参数寻优,步骤如下:
(1)参数初始化。设置灰狼种群规模、最大迭代次数、参数γ和σ取值范围。
(2)计算灰狼个体适应度。将预测值与实际值的均方差作为适应度函数,并对灰狼个体适应度进行计算,选择出当前最优适应度前三的个体,分别作为α狼、β狼和δ狼。
(3)灰狼位置更新。运用灰狼优化算法在整个可行域内搜索,不断地更新α狼、β狼和δ狼以及猎物的位置。每次迭代后,重新计算适应度并进行比较,找出并更新至最优位置,若达到迭代次数或满足精度,则将其输出最优参数组合(γ,σ),否则返回继续寻优。
(4)将寻优得到的最优参数组合建立并代入到LSSVM预测模型。
2 GRA-GWO-LSSVM预测模型
根据上述分析过程,首先利用GRA对输入样本进行关联度计算,筛选出影响研究对象的主要因素,并作为预测模型输入变量,另外通过GWO算法对LSSVM的惩罚参数γ和核函数参数σ进行寻优,并最终得到对应的模型及其预测结果。组合预测模型流程如图1所示。
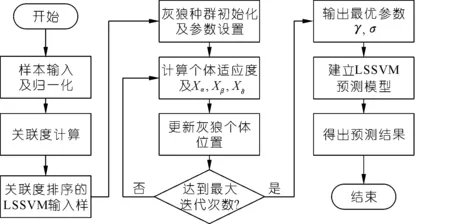
图1 GRA-GWO-LSSVM模型流程
3 实例分析
3.1 样本收集和关键因素提取
AOP主要与爆破参数、装药工艺、岩石性质、天气情况等因素有关。本文根据已有文献研究和爆破工程实际情况,初步选出炮孔深度(HD)、炮孔直径(BD)、堵塞长度(ST)、排距(B)、炮孔间距(S)、最大段药量(MC)、炸药单耗(PF)、爆心距(D)、相对湿度(RH)、岩石质量指标(RQD)10个影响因素对AOP强度进行研究。
贵州省兴义市小河边水库大坝坝体混凝土浇筑量约为21.5万m3,下游、上游边坡比分别为1.5∶1和1.75∶1,大坝库容约为240万m3。在此次爆破工程中,通过使用Instantel振动监测仪监测了距离爆破中心250~500 m的AOP,其中爆心距通过全球定位系统GPS测量。最终获得了40组有效样本数据,如表1所列。
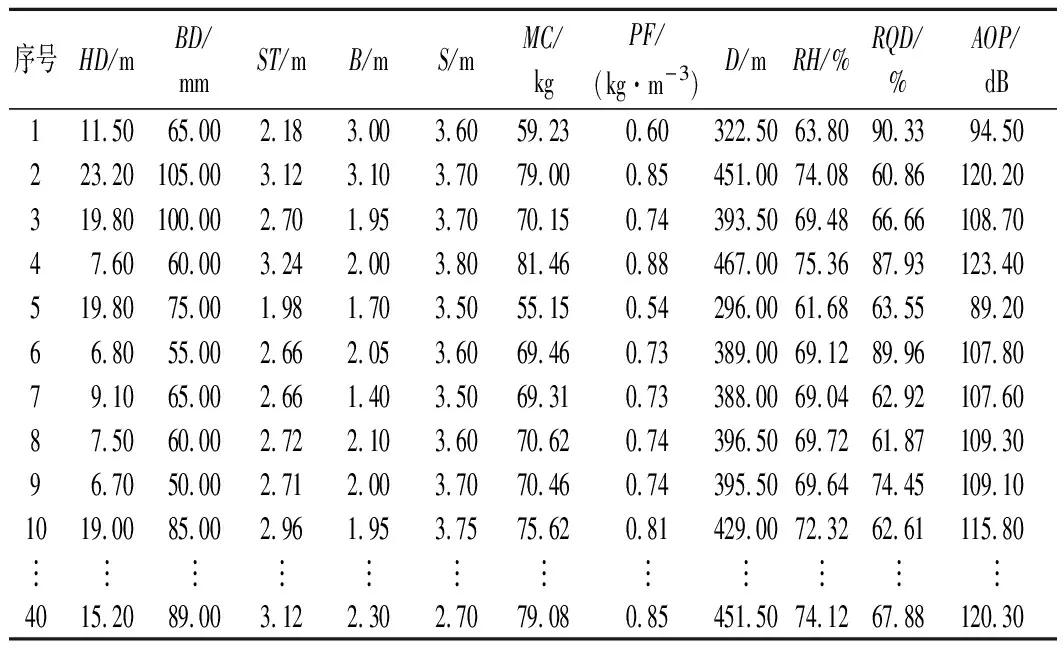
表1 预测模型的样本数据
利用灰色关联分析法分析影响AOP的关键因素,结果如图2所示,可以看出:最大段药量(MC)、相对湿度(RH)、爆心距(D)、炸药单耗(PF)、堵塞长度(ST)这5个影响因素的灰色关联度大于阈值0.8,对AOP影响程度较大,因此将这5个关键因素作为预测模型的输入变量,将AOP强度作为预测模型的输出变量。
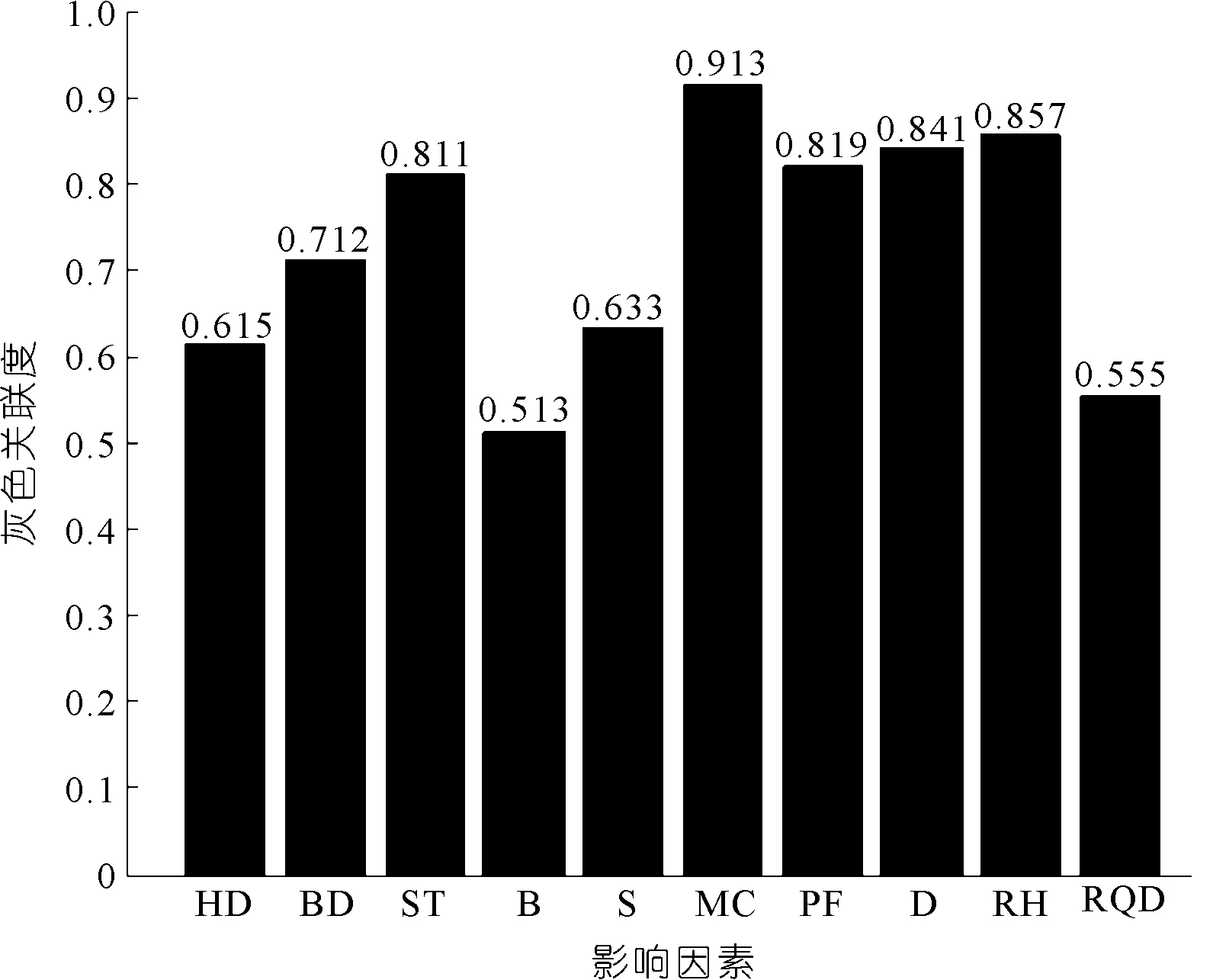
图2 灰色关联度柱状图
3.2 预测结果与比较分析
本文选取样本数据中前32组(80%)作为预测模型训练样本,后8组(20%)作为预测样本,经过数据预处理后代入该模型。其中,GWO算法初始化参数设置如下:狼群种群数量取20,最大迭代次数取100,惩罚参数γ和核函数参数σ均设置在[0.01,100]之间。训练得最优参数组合(γ,σ)=(3.232,10.261),代入到LSSVM模型中进行预测分析。
为论证该模型优越性,分别将GRA-GWO-LSSVM模型、GWO-LSSVM模型与PSO-LSSVM模型的预测结果进行对比分析,结果如表2所列。由表2可知:GRA-GWO-LSSVM模型预测值仅有个别点误差较另外两种模型偏大,但是其总体相对误差为2.87%,显然优于GWO-LSSVM模型的3.75%,和PSO-LSSVM模型的5.89%。
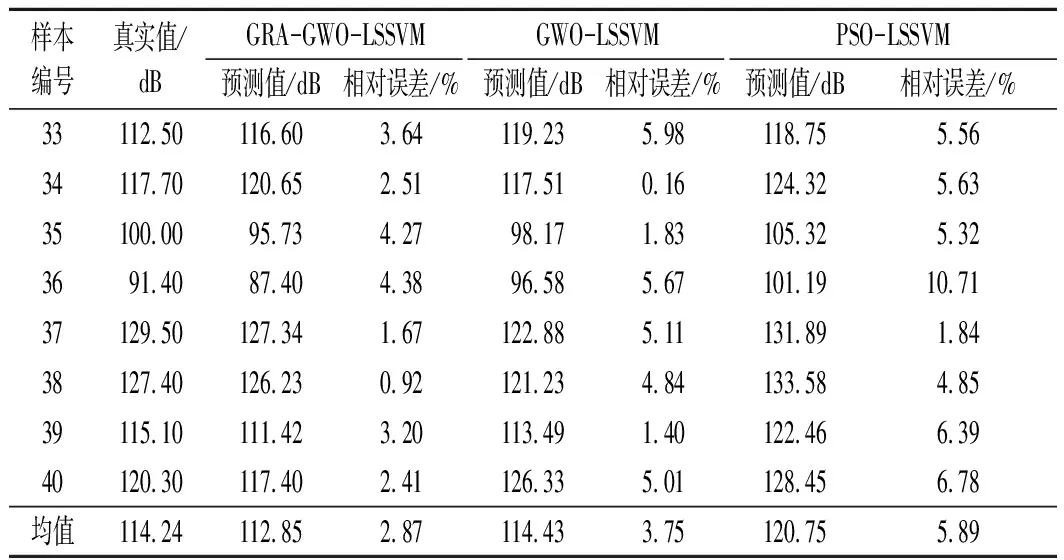
表2 不同模型相对误差对比
为了进一步比较组合模型的拟合与预测精度,引入如下模型评价指标:
(10)
(11)
(12)
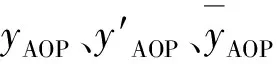
计算得出表3所列的评价指标对比结果。由表3可知,GRA-GWO-LSSVM预测模型的RMSE与MAE分别为3.31和3.15,且明显小于另外2种模型,另外GRA-GWO-LSSVM预测模型的R2为0.93,比GWO-LSSVM模型的0.83和PSO-LSSVM的0.74更接近于1。综上分析,通过GRA对影响因素进行筛选,剔除冗杂因素,能有效降低预测模型复杂度,相比于PSO,利用GWO对LSSVM参数优化的效果更好,所以GRA-GWO-LSSVM预测模型预测值更贴近于真实值,拟合效果较好。
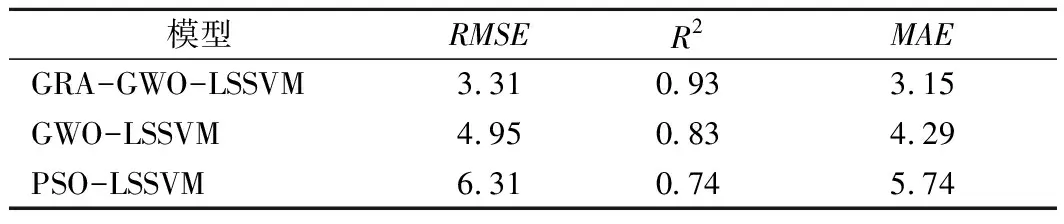
表3 模型评价指标结果对比
4 结 论
针对爆破工程中AOP造成的环境与安全的不良影响,通过选取最大段药量(MC)、爆心距(D)、相对湿度(RH)、炸药单耗(PF)、堵塞长度(ST)作为主要因素,构建基于GRA-GWO-LSSVM的爆破空气超压预测模型,初步得出以下结论:
(1)AOP影响因素多,样本检测数据获取困难,通过使用GRA筛选出关键因素,能有效避免冗杂因素对模型干扰,提高预测精度。
(2)利用灰狼优化算法(GWO)其全局搜索能力强、调用参数少等优点来对LSSVM的惩罚参数和核函数参数寻优,解决了传统方法在寻找参数时人工试算的问题,提高了模型学习能力和泛化能力。
(3)GRA-GWO-LSSVM预测模型对于AOP预测具有适用性,相比于GWO-LSSVM模型和PSO-LSSVM模型预测,其预测精度更高,拟合效果更好。
